Mar
9
¿D-branas? ¿Qué es eso?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
¿Qué son las D-branas? ¿Por qué las requiere la teoría de cuerdas? La respuesta básica a la segunda pregunta es que dan sentido a las cuerdas abiertas que intervienen en la teoría tipo I: cada uno de los dos extremos de una cuerda abierta debe residir en una D-brana. Pero dos extremos de la cuerda abierta residen en un subespacio (q + 1)-dimensional de género tiempo llamado una D-brana, o D-q-brana que es una entidad esencialmente clásica (aunque posee propiedades de supersimetría), que representa una solución de la teoría de supergravedad 11 dimensional.
En respuesta a la primera pregunta, una D-brana es una estructura de género tiempo, como más arriba indico, 1 + q dimensiones espaciotemporales. Invocando una de las dualidades de la teoría M, alternativamente podemos considerar una D-brana como una solución de las ecuaciones de alguna otra versión de la teoría M de cuerdas.
Las D-branas aparecen en muchas discusiones modernas relacionadas con las cuerdas (por ejemplo, en la entropía de los agujeros negros). Suelen tratarse como si fueran objetos clásicos que yacen dentro del espacio-tiempo completo 1 + 9 (o 1 + 10) dimensiones. La “D” viene de “Dirichlet”, por analogía con el tipo de problema de valor de frontera conocido como un problema de Dirichlet, en el que hay una frontera de género tiempo sobre la que se especifican datos (según Peter G. Lejeune Dirichlet, un eminente matemático francés que vivió entre 1.805 y 1.859).
Con la introducción de tales D-branas, varios teóricos han expresado una “filosofía de cuerdas” que parece representar un profundo cambio respecto a lo anterior. En efecto, se afirma con cierta frecuencia que podríamos “vivir en” esta o esa D-brana, lo que significa que nuestro espacio-tiempo percibido podría yacer realmente dentro de un D-brana, de modo que la razón de que no se perciban ciertas “dimensiones extra” se explicaría por el hecho de “nuestra” D-brana no se extiende a esas dimensiones extra.
La última posibilidad sería la postura más económica, por supuesto, de modo que “nuestra” D-brana (una D-3-brana) sería de 1 + 3 dimensiones. Esto no elimina los grados de libertad en las dimensiones extra, pero los reduce drásticamente. ¿Por qué es así? Nuestra perspectiva ahora es que somos “conscientes” de los grados de libetad que están implicados en el interior profundo del espacio de mayores dimensiones entre las D-branas, y es en esto donde se está dejando sentir la excesiva libertad funcional.
Sólo vamos a ser conscientes de dimensiones extra allí donde inciden directamente sobre las D-brana en la que “vivimos”. Más que una imagen de tipo “espacio cociente” que evoca la analogía de Kaluza-Klein original:
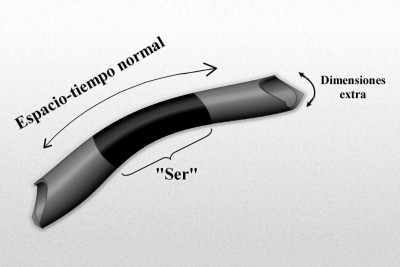
El gráfico representa un modelo de manguera de un espacio-tiempo de dimensiones más altas de tipo Kaluza-Klein, donde la longitud, o mejor, la dimensión a lo largo de la longitud de la manguera representa el 4-espacio-tiempo normal, y la dimensión alrededor de la manguera representa la dimensión extra “pequeñas” (quizá escala de Planck). Imaginemos un “ser” que habite en este mundo, que rebasa estas dimensiones extra “pequeñas”, y por ello no es realmente consciente de ellas.
Así, nuestro espacio-tiempo observado aparece ahora como un subespacio 4-dimensional del espacio real de dimensiones más altas. Con algo de imaginación, lo podemos visualizar en nuestra mente.
¿Cuánta libertad funcional esperamos ahora? La situación es ahora algo parecida a la imagen geométrica que hemos adoptado en el gráfico para obtener una perspectiva más convencional con respecto a la “supergeometría”. Puesto que ahora estamos interesados solo en el comportamiento en la D-brana (que suponemos que es geométricamente una (1 + 3)-superficie ordinaria), podemos imaginar que nuestra libertad funcional se ha convertido en una aceptable ![]() , aunque para un M bastante grande. Sin embargo, incluso esto supone que la restricción de la dinámica en el 10-espacio (un 11-espacio) completo nos proporciona ecuaciones dinámicas dentro de “nuestra” D-brana 4-dimensional que son del tipo convencional, de modo que bastarán los datos iniciales en una 3-superficie para determinar el comportamiento en todo el 4-espacio. Esto es difícilmente probable, en general, de modo que aún cabe esperar un excesivo
, aunque para un M bastante grande. Sin embargo, incluso esto supone que la restricción de la dinámica en el 10-espacio (un 11-espacio) completo nos proporciona ecuaciones dinámicas dentro de “nuestra” D-brana 4-dimensional que son del tipo convencional, de modo que bastarán los datos iniciales en una 3-superficie para determinar el comportamiento en todo el 4-espacio. Esto es difícilmente probable, en general, de modo que aún cabe esperar un excesivo ![]() . ¡El problema no ha desaparecido todavía!
. ¡El problema no ha desaparecido todavía!
Tal actitud hacia las D-branas se ha utilizado para intentar resolver el problema de la jerarquía del gráfico siguiente:
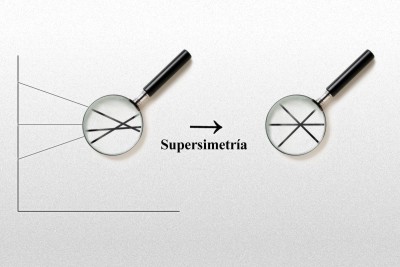
Según cierta perspectiva de “gran unificación”, las constantes de acoplamiento de las interacciones fuerte, débil y electromagnética, tratadas como constantes de acoplamiento móviles, deberían alcanzar exactamente el mismo valor a temperaturas suficientemente grandes, aproximadamente 1028 K, que se habrían dado alrededor de 10.000 instantes de Planck después del Big Bang (~10-39 s). Se ha visto que la supersimetría es necesaria para resolver que los tres valores coincidan exactamente.
En concreto, esta es la cuestión de por qué las interacciones gravitatorias son tan minúsculas comparadas con las demás fuerzas importantes de la naturaleza o, de manera equivalente, por qué es la masa de Planck tan enormemente mayor que las masas de las partículas elementales de la naturaleza (en un factor de, aproximadamente, 1020). La aproximación de la D-brana a este problema parece requerir la existencia de más de una D-brana, una de las cuales es “grande” y la otra “pequeña”. Hay un factor exponencial involucrado en cómo se estira la geometría desde una D-brana hasta la otra, y esto se considera una ayuda para abordar la discrepancia en 1040, más o menos, entre las intensidades de la fuerza gravitatoria y las otras fuerzas.
Se puede decir que este tipo de imagen de espacio-tiempo de dimensiones más altas, que se estira desde la frontera de una D-brana hasta la otra, es uno de los tipos de geometría sugeridos por las teorías 11 dimensionales, tales como la teoría M, donde la undécima dimensión tiene la forma de un segmente abierto, y la geometría de cada frontera tiene la forma topológica (por ejemplo, M×V) de los 10 espacios considerados antes. En otros modelos, la undécima dimensión es topológicamente S1.
¿Qué harán de todo esto los físicos con respecto al estatus de la teoría de cuerdas como una teoría física para el futuro?
La situación tiene aspectos muy enigmáticos y notables, y otros aspectos parecen inconsistentes y sería un error, en este momento, que los demos por buenos; mejor esperemos a que maduren. Pese a todo, muchas de las afirmaciones de los teóricos de cuerdas se hacen con gran seguridad y aparente confianza. Es indudable que estas afirmaciones deben ser suavizadas hasta que se adquiera más certeza en el conocimiento de los múltiples aspectos de la teoría que deben ser tomados con cierta reserva antes de ser lanzadas alegremente al mundo.
Roger Penrose afirma que algunas de las afirmaciones de más peso pueden ser descartadas (tal es el caso de que la teoría de cuerdas ha proporcionado una teoría completa y consistente de la gravedad cuántica). En mi modestia, estoy totalmente de acuerdo con él, y según lo poco que sé al respecto, me hace pensar que la teoría de cuerdas es una firme candidata para llegar a esa teoría cuántica de la gravedad, aunque de momento, le queda inalcanzable.
No obstante, sería injusto no admitir que parece haber algo de auténtica trascendencia “entre bastidores” en algunos aspectos de la teoría M de cuerdas. Claro que podría resultar que ese algo sea de interés puramente matemático, sin que haya ninguna razón real para creer que nos acerca más a los secretos de la naturaleza.
La teoría M de cuerdas es una teoría muy adelantada a su tiempo; incluso las matemáticas necesarias para desarrollarla al completo nos son desconocidas. Por otra parte, la energía necesaria para verificarla no está a nuestro alcance.
La fuerza del argumento a favor de la teoría de cuerdas parece residir en varias relaciones matemáticas notables entre “situaciones físicas” en apariencia diferentes, normalmente, algo alejadas de la física del mundo real de la naturaleza. ¿Son una coincidencia estas relaciones, o hay alguna razón más profunda tras ellas?
Si hablamos de matemáticas, las coincidencias sin una razón determinada suelen ser más bien escasas. Me inclino y apuesto por el hecho de que para muchas de estas “coincidencias” hay realmente una razón, todavía no descubierta. Algunos, no sé si calificarlos de envidiosos o de tener carencia de ilusiones, han llegado a decir que, los teóricos de cuerdas no es seguro que estén haciendo física, o si la hacen, ¿qué área de la física están explorando realmente? Se me ocurre pensar que el mismo escepticismo encontró a Einstein en su tiempo, al formular sus famosas teorías relativistas, y sin embargo, nos trajo hasta aquí.
No parece que se pueda hacer una valoración adecuada de estas cuestiones sin mencionar el papel concreto de Edward Witten. Él es aceptado generalmente como la figura con más responsabilidad en la dirección de la investigación en la teoría de cuerdas (y la teoría M) desde finales de la década de los 80. Ha tenido un papel primordial en el lanzamiento de la “segunda revolución en supercuerdas” en 1.995, pero ya entonces había establecido su preeminencia al iniciar varios desarrollos importantes en la teoría de cuerdas, y en muchas otras áreas que tienen cierta relación (no siempre obvia) con la teoría de cuerdas. Sin duda, Witten ha sido hasta el momento el mejor conductor de la teoría de cuerdas.
Es interesante que en un nuevo trabajo que parece bastante importante, Witten ha vuelto a consideraciones dentro de un espacio-tiempo 4-dimensional estándar (aunque sigue habiendo supersimetría). Combinando ideas de la teoría de twistores y la teoría de cuerdas, Witten es capaz de obtener algunos resultados fascinantes concernientes a las interacciones de Yang-Mills de varios gluones. Este trabajo es particularmente importante desde una perspectiva orientada a los twistores, y bien podría llevar a nuevos desarrollos.
La calidad de los logros intelectuales de Witten es extraordinaria. Se puede comentar, por ejemplo, sobre los seminarios de matemáticas de Oxford (en la serie de geometría y análisis), en los que se ha anunciado algún informe nuevo y muy original de algún problema, y ha resultado que la idea seminal procedía en realidad de Witten. A menudo, tales enfoques han abierto un nuevo campo, donde estas ideas imprevistas y nuevas han arrojado un potente fogonazo de luz original sobre problemas matemáticos difíciles (a veces problemas que previamente parecían intratables). Sin duda, Witten posee una extraordinaria intuición y unos conocimientos matemáticos que sobrepasan a los de primer orden; su medalla Field de 1.990 es más que justificada. Sin embargo, sus capacidades, según las ideas que expone, están más cerca de la observación profunda de la naturaleza. Si él tiene razón, entonces quizá éste sea uno de los argumentos más contundentes para aceptar sus opiniones de que la supersimetría y la teoría de cuerdas encuentran un profundo favor en la naturaleza. Por otra parte, ¡quizá sea un matemático más notable de lo que él mismo admite!
De todas maneras, soy partidario de no apostarlo todo al mismo caballo; está claro que la teoría de cuerdas me encanta, y sus perspectivas futuras me entusiasman. Sin embargo, no quiero descartar otros caminos, otras ideas, otros puntos de vista dirigidos en otras direcciones porque, ¿dónde está la verdad?
emilio silvera
















 Totales: 75.615.134
Totales: 75.615.134 Conectados: 63
Conectados: 63






















