Concepto de Campo

Pasemos ahora al concepto de «campo», que se elaboró en el siglo XIX, mucho antes de que se ideasen la mecánica cuántica v la teoría de la relatividad especial o restringida. Los campos más conocidos son entidades físicas como el campo eléctrico o el magnético, que manifiestan su existencia en nuestra vida cotidiana. Son invisibles y, sin embargo, influyen en la materia; un campo magnético atrae el hierro, por ejemplo. Hoy los físicos creen que todas las partículas cuánticas (electrones o quarks) son manifestaciones de diferentes tipos de campos. Pero, ¿qué son los campos?

En nuestro limitado espaciotiempo de cuatro dimensiones podríamos contentarnos con la noción un poco abstracta de «campo», una propiedad no geométrica que adquiere el espacio cuando hay una carga cerca. De allí sale la expresión «campo eléctrico» y «campo magnético» que son frecuentemente escuchados en nuestra vida cotidiana. La carga lleva consigo ese campo, se mueve con él, como si fuera una especie de halo. Sólo quienes llevan carga pueden ver este halo. Así, el neutrón no ve eléctricamente al protón; el electrón, en cambio, sí que lo ve, y gracias a la fuerza eléctrica, forma con él la variedad de átomos que conocemos.

Pero el concepto de campo no es tan restringido como lo hemos descrito en el párrafo anterior. Imaginemos un volumen grande de aire, como la masa de aire situada sobre un continente. Podemos asignar a cada punto del volumen de aire un número determinado que corresponda a la temperatura del aire en aquel punto. La temperatura del aire ejemplifica lo que los físicos llaman un «campo escalar»: una función numérica que expresa una magnitud (la temperatura del aire) que varía de un punto a otro del espacio. Podemos suponer también que este campo de temperatura es una función del tiempo; la temperatura cambia continuamente de hora en hora.

Son también posibles otros tipos de campos. Supongamos, por ejemplo, que el aire se mueve, como suele hacerlo. Podemos, pues, concretar un vector en cada punto de él, un objeto matemático con una magnitud, que expresa la velocidad del aire en ese punto, y una dirección, que es aquella en la que se está moviendo el aire en ese punto. Podemos imaginar el vector como una flecha ligada a cada punto en el espacio. La velocidad del aire a través del espacio es un ejemplo de «campo vectorial»: tiene a la vez magnitud y dirección, y además puede cambiar a lo largo del tiempo.

Los campos como los mencionados de la temperatura y la velocidad del aire pueden ser estáticos y no moverse, o moverse despacio, o del modo que se propaga un campo ondular a través del medio. El movimiento de campos en el espacio y el tiempo se describe matemáticamente mediante un conjunto de «ecuaciones de campo».

Los campos también pueden interactuar unos con otros. Por ejemplo, si en cierta región la temperatura es baja, comenzará a desplazarse hacia ella aire más cálido; el campo de temperatura escalar influye así en el campo de velocidad vectorial, y a la inversa.

Los físicos del siglo XIX conocían campos como el escalar y el vectorial que acabo de describir para el aire. Cada campo tenía necesariamente un medio asociado, y el campo de temperatura era la temperatura del medio atmosférico. Los campos ondulares se propagaban siempre en un medio, del mismo modo que se propagan en el aire las ondas sonoras. Parecía imposible que hubiese campos sin un medio que los sustentase.

Pero el concepto de campo se debe al gran Michael Faraday. Surgió en una época de gran efervescencia en Europa. El fin del siglo XVIII y el comienzo del XIX fueron tiempos de enorme creatividad. En medio de febriles cambios políticos inspirados por la Revolución Francesa, Mozart, Beethoven, Chopin y Schubert producían monumentos musicales, mientras en matemáticas abrían nuevas fronteras Karl Friedrich Gauss (llamado en su entorno Princeps Mathematicorum), Augustin-Louis Cauchy (789 memorias publicadas), Lazare Nicolas Marguerite Carnot (llamado el Organizador de la Victoria por sus acciones políticas), Evariste Galois (enfan terrible muerto en un duelo a los veinte años). Gaspard Monge creador de la geometría descriptiva, empieza su libro Traité de la Géométrie Descriptive (1798) ofreciéndolo para “liberar, la nación francesa de la dependencia de la industria extranjera”. ¡Qué tiempos de idealismo!

Es la época en que la electricidad acaba de nacer. Es inventada la pila o batería eléctrica por Alessandro Volta en el año 1800, la que se transforma en la delicia de los aficionados a experimentar con la corriente eléctrica, investigar cómo pasa por cada cable alámbrico, cómo cambia al variar la forma o la temperatura del material conductor, etc. Es una época muy propicia para hacer investigaciones que posteriormente llevan a importantes descubrimientos. Entre los más importantes, se cuentan los de Hans Christian Oersted. Mientras hacía una demostración en clase, en 1819, advierte de pronto que la corriente que pasa por un alambre desvía la aguja imantada de una brújula cercana. Puesto que la corriente no es más que un flujo de cargas, como de vehículos por una carretera, Oersted concluyó que el magnetismo debía tener su origen en el movimiento de cargas.

Lo anterior, sí que fue una sorpresa. Hasta entonces al magnetismo no se le relacionaba en nada con la carga eléctrica. Conocido en Grecia desde la antigüedad remota, en el siglo I a. de C. el poeta latino Tito Lucrecio relataba que “el hierro es atraído por esa piedra que los griegos llaman magneto por su origen en los territorios de los magnetes, habitantes de Magnesia, en Tesalia.

Aunque su origen natural es bien comprendido hoy, el halo de misterio y magia del magnetismo permanece. Existen una serie de creencias populares que le asignan poderes desde mágicos a curativos. Incluso existe un dicho por ahí, que dice: “la nación que controle el magnetismo, controla el universo”.

Después del descubrimiento de Oersted, André Marie Ampère hizo otro hallazgo bastante sorpresivo para lo que entonces se conocía del magnetismo. Usemos sus propias palabras, “Dos corrientes eléctricas se atraen cuando se mueven paralelamente y en igual dirección; se repelen cuando se mueven paralelamente y en direcciones opuestas”. La corriente no sólo desvía la aguja de un imán, sino que también ¡atrae o repele a otra corriente! Por ejemplo, los alambres que usamos en lámparas, televisores y otros artefactos, son dobles, como las carreteras de dos vías, para que las cargas puedan entrar por uno y salir por el otro. Es el cable «paralelo», como le suelen llamar. Pues bien, cuando encendemos el artefacto y la corriente alterna va y viene, los alambres del paralelo se repelen con una fuerza equivalente al peso de una pulga. Aunque pequeñísima, la repulsión siempre está presente.

Más de alguien pensará que eso no tiene nada de raro, porque cargas repelen a cargas. Razón tiene. Pero, los alambres son eléctricamente neutros; aunque se muevan, las cargas en su interior están compensadas como lo están en un átomo, hay tantas de un signo como del otro. No es entonces la mera fuerza de Coulomb entre cargas, sino algo nuevo, que se origina en su movimiento. La producen cargas que se mueven y la experimentan cargas que también se mueven. Este «algo nuevo» es justamente lo que llamamos campo magnético.

Cuando aparecen las palabras «campo magnético» en la mente de la mayoría que nos encontramos insertos, de una u otra forma, en el concepto de campos se nos viene el nombre de James Clerk Maxwell, un físico escocés del siglo XIX que fue el primero que formuló las ecuaciones que describen los campos eléctrico y magnético. Maxwell elaboró modelos mecánicos del campo electromagnético, máquinas compuestas de tornillos y mecanismos que imitaban las propiedades del campo. Maxwell adoptaba una posición ambivalente respecto a si los campos eléctrico y magnético necesitaban o no el medio del «éter», que entonces se creía que impregnaba todo el espacio. Muchos físicos partidarios del éter intentaron deducir sus propiedades de las de la luz cuando se propagaba en este medio extraño. Pero en su artículo de 1905 sobre la relatividad especial, Einstein demostró que si él no se equivocaba toda tentativa de detectar el llamado éter estaba condenada al fracaso… era un concepto superfluo. Los campos electromagnéticos no exigían un medio para propagarse, y en este sentido eran entidades básicas e irreductibles. A diferencia de los campos de velocidad y temperatura en el caso del aire, que podían reducirse a las propiedades de átomos de aire en movimiento, el campo electromagnético no tenía partes «atómicas».

Pero, como consecuencia del trabajo de Einstein, hoy día, la actitud de los físicos es bastante disímil hacia los campos básicos a la que imperaba en el pasado. Dichos campos no tienen que explicarse en función de otra cosa como el éter. Por el contrarío, los campos básicos (y hay varios, además del electromagnético) son, las entidades primarias por medio de las cuales pretendemos explicar todo lo demás. Como dijo Steven Weinberg: “La realidad esencial es un conjunto de campos… todo lo demás puede deducirse como consecuencia de la dinámica cuántica de esos campos.”

No deja de considerarse absurdo preguntar de qué están compuestos los campos como preguntar de qué «material» están hechas las partículas cuánticas. El criterio hoy predominante es que los campos son irreductibles, es decir, que no tienen partes; son las cosas más simples. Los campos, como el electromagnético y los demás con que nos encontraremos, son entidades físicas que se hallan definidas con toda sencillez mediante las ecuaciones de campo que expresan sus cambios y que se clasifican según cómo se transforman en diversas operaciones de simetría y por sus interacciones con otros campos. Una vez especificadas estas propiedades, queda exactamente definido el campo.

Ahora bien, creo que nos corresponde distinguir aquí, en esta parte de esta sección, la clases de campos que reconocemos los que, de una u otra manera, con frecuencia tenemos que trabajar – en nuestro quehacer diario – inmersos en ellos. Sí exigimos que obedezcan la teoría einstiana de la relatividad especial, podemos utilizar el sistema de clasificación de Wigner. Como explicaré posteriormente con algún detalle, cada campo se corresponde con una partícula cuántica diferenciada, con un espín y una masa específicos, la base de su clasificación. Algunos campos corresponden a partículas cuánticas sin masa. Estos campos, entre los que se incluyen el electromagnético y el gravitatorio, son de amplio alcance; se extienden a lo largo de grandes distancias, y, en consecuencia, nos resulta fácil detectar su presencia. Otros campos describen las interacciones de partículas cuánticas de gran masa. Éstos son de muy corto alcance; sólo se alcanzan en el espacio distancias microscópicas atómicas o subnucleares.

Si consideramos cómo se transforman los campos si los sometemos a un movimiento de rotación, podemos asignarles un espín. Naturalmente, el spin asignado corresponde al concreto de la partícula cuántica asociada con el campo. El campo electromagnético tiene espín uno, igual que los fotones. El campo de Dirac tiene espín un medio, igual que el electrón, y otros tipos de campos tienen espín cero o tres medios o dos. Los trabajos de Wigner permiten clasificar todo tipo de campos a partir de la masa y el espín.

Pero también existen otras propiedades coadyuvantes de los campos que ayudan a su clasificación. Entre ellas están los diferentes tipos de cargas, como la carga eléctrica. Lo mismo que la propiedad del espín de un campo se relacionaba con su simetría espaciotemporal, así también las cargas de los campos se relacionan con simetrías adicionales denominadas «simetrías internas». ¿Cómo podemos explicar estas simetrías de carga «internas» adicionales? ¿Qué son?

Hasta ahora, hemos estado viendo campos individuales con spin y masa específicos. Corresponde, entonces, que veamos la condición de varios campos, todos exactamente con la misma masa y el mismo spin. En este caso, en general se habla de un solo campo, pero con varios componentes «internos». La idea básica de la simetría interna es que su actuación transforma los diversos componentes del campo unos en otros, de modo tal que la situación física permanece inmutable.

Para que podamos entenderlo, podemos concurrir a imaginarnos dos campos del mismo género que ocupan todo el espacio; denominemos a uno de ellos el campo «rojo» y al otro el «azul». El utilizar colores para diferenciarlos no tiene connotación alguna; podríamos utilizar igual números y denominarlos campos 1 y 2. Análogamente a lo que sucedía en el campo de temperatura del aire, supongamos que en el punto x del espacio, tenemos una «temperatura en rojo» TR(x) y una «temperatura en azul» TA(x), que son las magnitudes de los dos campos en el punto x. Supondremos, sin embargo, que la energía de los dos campos depende sólo de la cantidad T(x), que viene dada por la fórmula T2(x) = T(x) + T(x), es decir, que el cuadrado de T es la suma de los cuadrados de TR y TA.

Podríamos inferir a continuación que «rojo» y «azul» indican ejes en un espacio «interno» bidimensional (que nada tiene que ver con el espacio físico real) y que la magnitud del campo rojo y la del azul en el espacio real, se miden sobre los ejes «rojo» y «azul» en el espacio interno. Una rotación de los ejes en este espacio interno imaginario (una operación de simetría interna) altera la cuantía relativa de los componentes rojo y azul del campo, pero deja invariable la cantidad T(x) porque es el radio de un círculo, que no cambia aunque los ejes experimenten una rotación.

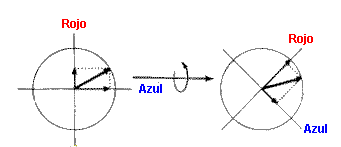
La magnitud de los campos «rojo» y «azul» en un punto del espacio viene indicada por la longitud de las flechas en los ejes rojo y azul de un espacio «interno» imaginario. Si se hacen girar los ejes de este espacio interno, cambian las magnitudes de los campos rojo y azul. Pero la energía total del campo, que sólo depende de la longitud del radio, no cambia. Lo cual indica una simetría «interna» de los componentes del campo.

Pero pensemos que realizamos una rotación matemática de este género transformando el componente rojo en azul y el azul en rojo. Esta rotación dejaría invariable de todos modos T(x), y, en consecuencia, la energía total. De esta manera, la situación física descrita por las ecuaciones de campo permanecería también invariable: las interacciones de los dos campos de componentes no dependen de la cuantía de la rotación de los campos rojo y azul. Aquí nos encontramos con una nueva simetría: el mundo no se modifica por rotaciones en este espacio interno de los componentes del campo. ¿Qué significa esto?

Los físicos saben que las invarianzas en operaciones de simetría, como la rotación que acabamos de describir, implican la existencia de cantidades conservadas, como la carga eléctrica, que van asociadas con el campo multicompuesto. Esto se puede entender con facilidad. Una simetría, de por sí, implica que hay algo que no cambia, que hay una invarianza del mundo. Para que haya invarianza ha de haber conservación de algo y, en el caso de las simetrías internas, será la conservación de cargas diversas. Sabemos que las simetrías de campos multicompuestos implican que los campos poseen cargas que se conservan en sus interacciones. Ya señalamos en la sección anterior que la matemática Emmy Noether formuló de modo matemáticamente preciso esta relación de la simetría con las leyes de conservación y proporcionó así una de las razones principales para que los físicos teóricos busquen nuevas simetrías.

Si bien los campos multicompuestos con «simetrías internas» pueden interactuar y mezclarse desordenadamente, sus cargas no varían nunca. De ahí, que tales cargas (consecuencia de la simetría) aporten otro dato permanente, por medio del cual pueden clasificarse los campos. Por ejemplo, si alguien le dice a un físico que un campo tiene una masa de 0,51 millones de eV, de espín 1/2 y de carga eléctrica menos uno, el físico sabrá enseguida que se trata de un campo electrónico.

El espacio interno, en vez de ser sólo bidimensional como en el caso de los campos «rojo» y «azul», puede tener varías dimensiones, correspondientes a los diversos componentes del campo. La transformación puede ser no ya una simple rotación de eje en el plano bidimensional, sino muchísimo más compleja; pero la idea básica seguirá siendo la misma: sí los componentes de un campo múltiple se pueden transformar unos en otros sin que varíen las interacciones del campo, hay sin lugar a dudas una simetría, junto con una ley relacionada de conservación de carga.

Hemos visto ya el papel importantísimo de la simetría en nuestra comprensión de los campos. Los campos se definen, en realidad, según se transforman en diversas operaciones de simetría. Los campos no son sustancias etéreas que ocupan el espacio y se mueven en el tiempo; son entidades irreductibles que poseen carga, espín y masa específicos, propiedades definidas todas ellas por operaciones de simetría. En cuanto se especifican tales propiedades, se ha dicho también completamente lo que es un campo.

El concepto clásico de campo es una de las ideas más trascendentales de la ciencia moderna. Aporta un lenguaje matemático simbólico para describir el mundo físico real, un lenguaje que cuando se domina plenamente no deja ya margen para una reducción mayor de significado. Para superar el concepto de campo, como quizá se haga en el futuro, habrá que modificar radicalmente nuestros conceptos de espacio, tiempo y simetría. La teoría de campo es hoy el idioma que utilizan los físicos para hablar del orden material básico del cosmos.

Texto extraído de Astrocosmo

[?]