Riemann nos explicó como es el Universo

Pero volvamos al trabajo de Riemann. Su propósito era introducir un nuevo objeto en las matemáticas que le capacitase para describir todas las superficies, por complicadas que fueran. Ésto le condujo inevitablemente a reintroducir el concepto de campo de Faraday.

El campo de Faraday, recordémoslo, era como un campo de granjero que ocupa una región de un espacio bidimensional. El campo de Faraday ocupa una región de un espacio tridimensional; a cualquier punto del espacio le asignamos una colección de números que describe la fuerza eléctrica o magnética en dicho punto. La idea de Riemann consistía en introducir una colección de números en cada punto del espacio que descubriera cuánto estaba torcido o curvado.

Por ejemplo, para una superficie bidimensional ordinaria, Riemann introdujo una colección de tres números en cada punto que describe completamente la curvatura de dicha superficie. Riemann descubrió que en cuatro dimensiones espaciales se necesita una colección de diez números en cada punto del espacio para describir sus propiedades. Por muy retorcido o distorsionado que esté el espacio, esta colección de diez números en cada punto es suficiente para codificar toda la información sobre dicho espacio. Hoy, esta colección de números se denomina el Tensor métrico de Riemann.  Hablando crudamente, cuanto mayor es el valor del tensor métrico, mayor es el arrugamiento de la superficie, digamos de una hoja de papel, y el tensor métrico nos da un medio sencillo para medir la curvatura en cada punto.  Si alisamos completamente la hoja arrugada, entonces recuperamos la fórmula de Pitágoras.

El tensor métrico de Riemann le permitió erigir un potente aparato para describir espacios de cualquier dimensión con curvatura arbitraría. Para su sorpresa, encontró que todos estos espacios están bien definidos y son autoconsistentes. Previamente, se pensaba que aparecerían terribles contradicciones al investigar el mundo prohibido de dimensiones más altas. Riemann no encontró ninguna. De hecho, resultaba casi trivial extender su trabajo a un espacio N-dimensional. El tensor métrico se parecía ahora a un tablero de ajedrez de N x N casillas.

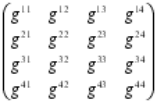
El tensor de Riemann contiene toda la información necesaria para poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico tiene diez números independientes).

De hecho, en las nuevas teorías de supercuerdas, planteadas en diez y veintiséis dimensiones, tendríamos que hablar del supertensor métrico de Riemann y de cientos de componentes.

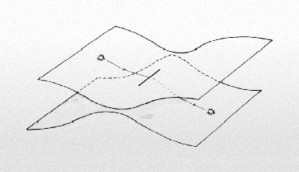
Gráfico: Un corte de Riemann, con dos hojas conectadas a lo largo de una línea.  Si caminamos alrededor del corte, permanecemos dentro del mismo espacio.  Pero si atravesamos el corte, pasamos de una hoja a la continua.  Esta es una superficie múltiplemente conexa

De la lección de Riemann se deduce que en espacios multidimensionales se crea el principio de que el espacio múltiple (de más dimensiones) unifica las leyes de la naturaleza encajándolas en el tensor métrico como piezas de un rompecabezas N-dimensional.

Riemann anticipó otro desarrollo de la física; fue uno de los primeros en discutir espacios múltiples y conexos, o agujeros de gusano.

Topológicamente hablando, el dibujo adjunto es equivalente a lo que sería un agujero de gusano con boca de entrada y de salida en regiones que nos llevarían a otro tiempo (así lo aseguró en 1.988, el físico Kip S. Thorne, del MIT ­- Instituto Tecnológico de Massachuse en California -).

El legado de Riemann (a pesar de su muerte prematura) fue extenso y en general muy valioso. En 1958, anunció incluso que finalmente había logrado una descripción unificada de la luz y la electricidad. Escribió: “Estoy completamente convencido de que mi teoría es la correcta, y de que en pocos años será reconocida como tal“. Aunque su tensor métrico le proporcionó un medio poderoso de describir cualquier espacio curvo en cualquier dimensión, él no conocía las ecuaciones exactas a que obedecía el tensor métrico; es decir, no sabía quçe es lo que hacía que la hoja se arrugase, eso lo vio seis décadas más tarde Einstein que se dio cuenta de que, en presencia de grandes masas, tales como planetas o estrellas – entre otros -, el espacio se “arruga” o “distorsiona”, se curva. Sin embargo Einstein sabía el origen de las arrugas y le faltaba el tensor métrico que, finalmente, le permitió legar al mundo su magnifica teoría.

El trabajo de Riemann, al utilizar el espacio multidimensional, logró simplificar las leyes de la naturaleza, es decir, para él, la electricidad y el magnetismo y también la gravedad eran simplemente los efectos causados por el arrugamiento o distorsión del hiperespacio.

Su asombroso trabajo (que no terminó), fue rematado por dos genios como Maxwell (electricidad y magnetismo) y Einstein (gravedad).

El mensajero de la cuarta dimensión, un pintoresco matemático inglés llamado Charles Howard Hinton que atravesó el Atlántico y la llevó a Norteamérica, formó bastante ruido a cuenta de la cuarta dimensión y se presentaba como experto en ella; tenía respuesta para cualquier pregunta.

Si le preguntaban ¿dónde está la cuarta dimensión?, su respuesta era invariable: “Está aquí, con nosotros, pero es tan pequeña que no la podemos ver“.

Básicamente, la respuesta de Hinton fue la misma que después dieron Kaluza y Klein para su quinta dimensión (la famosa teoría que unía el electromagnetismo de Maxwell y la gravedad de Einstein mediante la ocurrencia de elevar la teoría einsteniana en una dimensión más) y las que han dado otros físicos y matemáticos para explicar las teorías decadimensionales. En todas, cuando nació el tiempo y el espacio, en el Big Bang, resultó que tres dimensiones espaciales y una de tiempo se expandieron con el universo; las otras dimensiones se quedaron compactados en minúsculos círculos en la longitud de Planck, es decir una distancia de 10^-33 cm que se formula mediante ,  donde G,  es la constante gravitacional de Newton, ħ es la constante de Planck racionalizada, y c es la velocidad de la luz en el vacío. Esa es una distancia que, hoy por hoy, nuestros aparatos tecnológicos (microscópicos electrónicos, etc), no están capacitados para alcanzar.

Hay asuntos que en física, matemáticas o astronomía, están esperando una respuesta clara, y sobre todo urgente.

Tenemos pendientes las preguntas sobre lo que encierra el número 137, ese número puro y adimensional que se relaciona con e, el electrón del electromagnetismo, con h, el cuanto de acción de la constante de Planck, y con c, la velocidad de la luz de la relatividad especial de Einstein. Es lo que denominamos constante de estructura fina que es igual a 1/137 y resulta de los productos de 2πe²/hc, pero, ¿por qué? El día que tengamos la respuesta habremos despejado los misterios encerrados en e, h y c.

También esperamos respuesta a preguntas pendientes en geometría de los objetos a la que se ha dado en llamar topología, es la rama de la matemática que se ocupa del estudio de las propiedades de los objetos que no cambian al deformarlos continuamente: estirarlos, achatarlos o retorcerlos. Siempre sin cortarlos ni pegarlos. Los topólogos no miran la distancia, puesto que se puede cambiar al deformar el objeto, sino nociones más sutiles.

Henri Poincaré, físico y matemático francés, allá por el año 1.904 planteó algo que desde entonces se conoce como: “La conjetura de Poincaré“.  La pregunta de Poincaré fue la siguiente: ¿Es la esfera la única variedad tridimensional para la cual toda curva se contrae?

Desde que planteó este dilema hace ya más de un siglo, parece que nadie ha resuelto tal problema.

Ya he hablado antes de nuestro mundo tetradimensional con tres dimensiones de espacio y una de tiempo, y el salto enorme que dio la geometría cuando llegó Riemann a mediados del siglo XIX para cambiar conceptos que prevalecieron más de 20 siglos.

Finalmente, en el mes de agosto de 2006, alguien llamado G. Perelman (un matemático ruso excéntrico) en el Congreso Internacional de Matemáticas que se celebró en Madrid, expondría la solución final de “La conjetura de Poincaré” que, según todos los indicios, había resuelto. Sin embargo, ni se presentó al Congreso ni a recoger la Medalla Field que se había previsto le entregara el rey de España en ese acto. Dijo que no merecía la pena explicar a todos aquellos que no comprendían la profundidad de su trabajo.

Este extraño personaje, que vive con su madre en un piso de menos de 60 m² y se mantienen con una corta pensión, se pasa el día investigando sus teorías y números, y en los ratos libres sale al campo a buscar setas. Ha rechazado ofertas millonarias de universidades y multinacionales. Sólo está interesado en su mundo particular, y cuando le parece, publica algún descubrimiento en internet.

La respuesta tan esperada en astronomía es el que alguien responda a la pregunta siguiente: ¿Qué es y donde está la energía y la materia oscura?

Sí, sabemos que su presencia puede ser inferida por sus efectos sobre los movimientos de las estrellas y galaxias, aunque no puede ser observada directamente debido a que emite poca o ninguna radiación. Se piensa que algo más del 90% de la masa del universo se encuentra en alguna forma de materia oscura. Existen evidencias de materia oscura en las galaxias espirales en sus curvas de rotación. La existencia de materia oscura en los cúmulos ricos de galaxias puede ser deducida por el movimiento de las galaxias constituyentes. Una parte de esta materia oscura puede encontrarse en forma de estrellas poco masivas u objetos con masa del orden de la de Júpiter; dicha materia normal se describe como bariónica (los bariones son los protones, neutrones y otras partículas formadoras de materia que podemos ver).  Por otra parte, también puede existir materia oscura en el espacio entre galaxias, ese espacio que llamamos vacío y que en realidad está abarrotado de partículas virtuales que aparecen sin saber de dónde y en manos de una millonésima de segundo desaparece sin que sepamos a dónde, y que podría hacer aumentar la densidad media del universo hasta la densidad crítica requerida para invertir la expansión actual.

Si la teoría del Bing Bang es correcta, como parece que lo es, debe de existir una gran proporción de materia oscura en forma no bariónica (que no podemos ver), quizás axiones, fotinos o neutrinos masivos, supervivientes de las etapas tempranas del Big Bang y, ¿por qué no?, también podríamos suponer que la materia oscura que tanto nos preocupa pudiera estar encerrada dentro de las singularidades de tantos y tantos agujeros negros que se han debido formar a lo largo de los 13.500 millones de años que es la edad del universo.

Los agujeros negros, cuya existencia se dedujo por Schwarzschild en 1.916 a partir de las ecuaciones de campo de Einstein de la relatividad general, son objetos supermasivos, invisibles a nuestra vista (de ahí su nombre) del que no escapa ni la luz; tal es la fuerza gravitatoria que generan que incluso engullen la materia de sus vecinas, objetos estelares como estrellas que osan traspasar el cinturón de seguridad que llamamos horizonte de sucesos.

Pues bien, si en el universo existen innumerables agujeros negros, por qué no creer que sean uno de los candidatos más firmes para que sea la buscada “materia oscura”.

Para mí particularmente, sin descartar absolutamente nada de lo anterior (cualquier teoría podría ser la cierta), la denominada materia oscura está situada en la quinta dimensión, y nos llegan sus efectos a través de fluctuaciones del “vacío”, que de alguna manera deja pasar a los gravitones que transportan la fuerza gravitacional que emite dicha materia y sus efectos se dejan sentir en nuestro universo, haciendo que las galaxias se alejen las unas de las otras a mayor velocidad de la que tendrían si el universo estuviera poblado sólo de la materia bariónica que nos rodea.

Nada…a seguir estudiando que nos queda mucho por saber.

emilio silvera

[?]