Final del homenaje a Boltzmann

La entropía creadora del orden

Pero volvamos a la famosa ecuación de Boltzmann, personaje objeto de este comentario, en la que se pueden deducir consecuencias inesperadas. Generalmente, la gente tiene asociada la entropía al desorden. Es ésta una idea heurística muy común que se deriva precisamente de la misma ecuación de Boltzmann: a mayor desorden, mayor cantidad de microestados, es decir, mayor entropía.

Los sistemas evolucionan siempre hasta alcanzar su estado de máxima entropía. Entonces, ¿qué significa el epígrafe o título que he puesto? ¿Cómo puede la entropía crear orden, si mayor entropía mayor desorden? No estoy seguro de que al final del comentario quien me esté leyendo haya recibido el mensaje que le quiero transmitir: la ecuación S = k log W es más sutil que cualquier interpretación heurística que pueda hacerse de ella, y veremos que, de acuerdo con esta ecuación, pueden simultáneamente en un sistema, aumentar la entropía y crearse estructuras ordenadas. Antes de pasar a ver algunos ejemplos que ilustran este fenómeno, empezaremos a recordar algunas cosas acerca del mecanismo de las transiciones de fase*.

Como es bien sabido, y acabamos de mencionar, la termodinámica nos enseña que, en ausencia de restricciones sobre un sistema que tiene una energía E y ocupa un volumen V, en equilibrio éste se encuentra en el estado en que la entropía es máxima. Es el conocido principio de máxima entropía. A la luz de la ecuación de Boltzmann, lo que esto significa es que encontraremos el sistema en el macroestado que está compuesto por un mayor número de microestados. Debido a la alta dimensionalidad del espacio de fases de un sistema de muchas partículas, “mayor número” es una manera sobria de referirse, en realidad, a un número abrumadoramente mayor; en otras palabras, prácticamente todos los microestados corresponden al macroestado de equilibrio (todo lo grande está formado de cosas pequeñas). Esa es la razón por la que es enormemente improbable encontrar el sistema en un microestado que no corresponda al macroestado de equilibrio. La ecuación, a la que continuamente hago referencias, proporciona así una excelente explicación del principio de máxima entropía.

Cuando un sistema está en contacto con un baño térmico a temperatura T, la energía deja de conservarse y lo que pasa a ser constante, a parte de la temperatura, es su promedio. La conservación del promedio de la energía impone una restricción al sistema, de modo que la entropía ya no puede alcanzar su valor máximo. De nuevo la termodinámica nos dice que, en ese caso, lo que se hace máximo es la entropía menos la energía media dividida entre la temperatura. Visto de otro modo, como el calor es Q = TS, otra forma de parafrasear el principio de máxima entropía es decir que el sistema, en equilibrio, distribuye la máxima cantidad de energía posible en grados de libertad que no producen trabajo (en calor). En ausencia de restricciones esto maximiza el calor Q, es decir, la entropía; si conservamos la energía media, entonces es Q – E, lo que se hace máxima.

La magnitud anterior tiene una interpretación en termodinámica: Q – E = TS – E = – F; F es la energía libre del sistema, la parte de la energía que puede transformarse en trabajo. El principio de máxima entropía se convierte, en un sistema isotermo, en el principio de mínima energía libre.

No quiero continuar la explicación mediante profundas y largas redacciones llenas de ecuaciones y ejemplos, en la mayor parte de los casos, ilegibles para el lector medio, así que insistiré sobre la sutileza de la ecuación que se denotó en páginas anteriores como S = k log W, y al mismo tiempo volver a la advertencia en contra de intuiciones heurísticas que puedan inducir a error (no se trata de que tengamos que dejar totalmente a un lado la intuición, pero sí es conveniente dejar siempre una puerta abierta al escepticismo – evitaremos sorpresas desagradables que llevan consigo la confianza ciega -).

La idea de orden y de aumento de entropía no es en absoluto incoherente, porque la ecuación arriba reseñada no identifica en absoluto entropía con desorden, y como ejemplo sencillo de ello, se me ocurre recurrir a una caja de frutero ocupada por frutas esféricas (naranjas). Tenemos que simular un sistema de esferas duras. La simulación consiste en situar N esferas en una caja cúbica de volumen V (lo que fija la densidad del fluido en p = N/V), y asignándoles una velocidades aleatorias, dejarlas evolucionar de acuerdo a las leyes de la mecánica. Cuando dos esferas se encuentran se produce una colisión elástica que se resuelve a partir de las ecuaciones de conservación de energía y momento. Al cabo de un tiempo de simulación, las partículas se encuentran en la fase de equilibrio a esa densidad (nótese que dado que no hay energía de interacción, la temperatura pasa a ser un mero factor de escala de las velocidades, siendo pues, irrelevante), o dicho de otra manera más precisa, presentan microestados correspondientes a dicha fase. Se puede observar en la simulación que las esferas muestran configuraciones desordenadas cuando la fracción de volumen ocupada era inferior al 50% aproximadamente, pero por encima de esa fracción, las esferas cristalizan en una red regular.

En vista del análisis del ejemplo anterior, esto no puede ocurrir… y sin embargo, ocurre; si no preguntemos a un frutero. Ellos saben desde siempre que la mejor manera de empaquetar naranjas (o cualquier otra fruta de forma más o menos esférica), es decir, la forma en que ocupan menos espacio, es apilándolas en una red ordenada. Lo que esto significa es que dicha red ordenada hace posible que el volumen accesible medio que corresponde a cada partícula es mayor que en una fase ordenada.

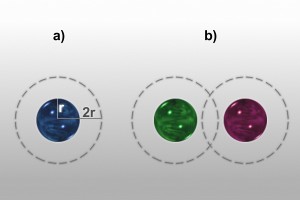
Esto puede resultar desconcertante: si hay N partículas en un volumen V, ¿no es V/N el volumen medio por partícula? En realidad no, porque hablamos de volumen accesible. Debido a que las esferas no se pueden penetrar, cada una tiene a su alrededor toda una esfera de radio 2r, siendo r el radio de las esferas, en la que no puede encontrarse ningún centro de masas de ninguna otra esfera (de lo contrario solaparían con ella).

Así que, en principio, el volumen accesible sería (V – vN)/N, siendo v el volumen excluido por una esfera. Pero esta cuenta sólo es válida a bajas densidades, cuando las esferas se encuentran, en promedio, muy alejadas unas de otras. A densidades superiores, cuando hay un gran número de esferas a una distancia entre centros de masa inferior a 4r, las esferas de exclusión de partículas vecinas se solapan (gráfico b), quedando pues, un volumen accesible mayor que cuando no lo hacían. Resulta ahora evidente que el volumen accesible total depende de la configuración concreta de las esferas, y su promedio, por tanto, dependerá de la fase en la que se encuentren. Así pues, sí puede ocurrir (y de hecho ocurre) que en la fase cristalina las esferas dispongan de más volumen accesible que en la fase fluida.

Lo que queda es trivial, recurriendo a la ecuación S = k log W, más volumen accesible significa un mayor número de microestados, lo que a su vez significa, según esta ecuación, mayor entropía; la fase ordenada tiene más volumen accesible por partícula, luego la fase ordenada tiene mayor entropía. Así de simple.

Terminaré este pequeño homenaje a Ludwig Boltzmann (cuya vida y obra pertenecen a la Historia, lugar virtual donde no todos podemos estar con el mismo relieve) con admiración hacia su obra.

Es curioso contemplar la generación de Boltzmann desde la perspectiva de nuestro siglo que nos deja apreciar que, por una parte, científicos como él, Kirchhoff , Helmholtz, Maxwell, Lord Kelvin, Hertz, Lorentz, J. J. Thompson, Max Planck y Poincaré, entre otros muchos, impulsaron y generaron un enorme crecimiento de la física pero que, por otra parte, fueron eclipsados por la figura de Einstein, convertido en el icono del físico por antonomasia. Situado en el macizo montañoso de tantas cumbres, la de Boltzmann apenas destaca, aunque sin duda su presencia contribuye a crear la línea de horizonte rocoso y sólido de la física de nuestro tiempo.

Aquí dejamos un recuerdo, mas de  100 años después de su muerte voluntaria en Duino, cerca de Trieste, de un gran físico que nunca se valoró en su justa medida.

emilio silvera

* Cambio de las características de un sistema. Volver

[?]