martes, 05 de noviembre del 2024 Fecha
Ir a la página principal Ir al blog

IMPRESIÓN NO PERMITIDA - TEXTO SUJETO A DERECHOS DE AUTOR



 

«
»

Nov

20

Comentario Breve de Física

Autor por Emilio Silvera    ~    Archivo Clasificado en Carnaval de Matematicas    ~    Comentarios Comments (6)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

Posiblemente, el descubrimiento de las leyes de la mecánica cuántica habría requerido más de un cuarto de siglo se la propia naturaleza no hubiera ayudado “regalándonos” la simplicidad del átomo de hidrógeno. Su espectro tiene la regularidad necesaria que permitió a Bohr empezar a comprenderlo a partir de las embrionarias ideas de Planck y de Einstein (uno con su cuanto de acción, h – la radiación de cuerpo negro –, y el otro con su trabajo inspirado en el anterior, y que versó sobre el efecto fotoeléctrico).

Si el átomo más elemental no constituyera un sencillo sistema “integrable” de dos cuerpos, la complejidad de su espectro hubiera retrasado el progreso hacia la física cuántica. Lo mismo puede decirse de la sencillez del sistema sol-planeta y del descubrimiento de las leyes de Kepler, que facilitaron enormemente el posterior descubrimiento de Newton y de la Ley de la Gravitación Universal, y la génesis de la ciencia moderna.

Por el contrario, la unificación de la mecánica cuántica con la gravitación, uno de los retos científicos fundamentales, no parece, al menos por el momento, que esté agraciada con la misma suerte.

La escala natural en la que la gravedad y la física cuántica se mirarían de igual a igual, viene dada por la longitud de Planck, , pero ésta resulta ser extraordinariamente pequeña, del orden de 10-33 cm, o en términos de masa-energía, , 10-8 g aproximadamente, o Ep = Mpc2 ≈ 1019 GeV. Esta masa está muy por encima de las masas de las partículas elementales y la energía muy lejos de las energías que pueden alcanzarse en varias generaciones venideras de los aceleradores.

El efecto físico más importante donde se combina la relatividad general  y la mecánica cuántica es el que descubrió Hawking en 1974. Los agujeros negros, en la teoría puramente clásica de la relatividad de Einstein, se comportan como objetos que absorben materia pero que no permiten dejar escapar nada de ella más allá del llamado horizonte de sucesos. Pero cuando la materia es tratada según la teoría cuántica, el agujero negro pasa a ser necesariamente emisor de radiación térmica.

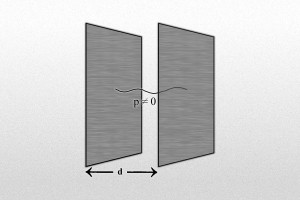
Uno de los efectos físicos más importantes que surgen cuando la geometría del espacio se “distorsiona” es el llamado efecto Casimir. En 1948, Casimir, motivado por el estudio de las fuerzas de Van der Waals, determinó la fuerza por unidad de área que se ejercen dos placas paralelas metálicas separadas por una pequeña distancia d:

efecto_casimir_formulaefecto_casimir

Confinamiento de un campo electromagnético en una región del espacio. Los modos del campo están obligados a anularse en los bordes de la región, definidos por las dos placas paralelas conductoras. Esta distorsión de los modos conduce, por comparación con la situación sin placas, a la existencia de una densidad de energía de vacío no nula.

Este efecto es interpretado como una manifestación de la existencia de una densidad de energía de vacío no nula debido al confinamiento del campo entre las dos placas. Aunque los valores promedios del campo sean nulos <Ø>, no ocurre lo mismo con <Ø2>, y por tanto, con la densidad de energía. Si consideramos por simplicidad un campo escalar sin masa, la densidad de energía de vacío que se obtiene por comparación con la del espacio completo (sin placas) -omito ecuación-

Para el campo electromagnético, el resultado difiere en un factor 2, que da cuenta de sus dos posibles polarizaciones, y el resultado final conduce a la fuerza por unidad de área dada anteriormente. Experimentos en laboratorios han confirmado de manera significativa el efecto Casimir, a pesar de su pequeña numérica: Fd4 ≈ -1’3×10-27 Nm2. Sin embargo, su significación conceptual el extraordinaria.

Kip S. Thorne nos dice que precisamente esa energía “exótica” que se produce de ese vacío entre las placas del efecto Casimir, puede ser utilizada para mantener abiertas las bocas de entrada y salida de los agujeros de gusano.

También se habla de aprovechar las enormes energías que están presentes en un Agujero negro pero, tanto esto como lo anterior, de momento, son sólo ¡sueños!

emilio silvera

emilio silvera

hotmail correo[?]


Esta entrada fue publicada el sábado, 20 de noviembre de 2010 a las 13:26 y está clasificada bajo: Carnaval de Matematicas. Puede hacer un seguimiento de los comentarios de esta entrada gracias al feed RSS 2.0. Puede dejar un comentario, o enviar un trackback desde su sitio.
 

  1. 1
    Iñigo
    el 21 de noviembre del 2010 a las 3:58

    De la formula se induce que al duplicar la escala las distancias se duplican, las areas se cuatriplican y la fuerza de Casimir se hace 4 veces mas debil. Si se divide sucesivamente la escala, tendria que existir alguna en donde la fuerza de Casimir entre particulas sea superior a cualquier fuerza fundamental, lo cual resulta curioso, por otro lado sino me equivoco la desintegracion de gamma en e- y e+ tendria que vencer el trabajo de Casimir
     
     

    Responder
  2. 2
    emilio silvera
    el 21 de noviembre del 2010 a las 10:43

    Buena lectura de la ecuación. De todos modos habría que profundizar algo más en esta variante que, como fuente de energía podría, algún día, ser muy necesaria para algunos de los proyectos futuristas que tenemos en mente.

    Son muchos los trabajos que sobre el tema se han realizado y, de manera constante se hacen pruebas y se llevan a cabo investigaciones para procurar que nos despejen el inmenso muro de ignorancia que nos separa de secretos de la Naturaleza que, como este mismo que aquí tratamos, nos podrían solucionar problemas del presente y del futuro.

    Aquí dejo otro punto de vista que, más o menos, viene a decir lo mismo que el trabajo que arriba he presentado.

    Cada campo tiene su vacío en la teoría cuántica de campos. Con el término vacío se entiende su estado de mínima energía. En general, en la teoría cuántica de campos los campos quedan descritos por una colección o serie de osciladores armónicos cuyos modos de oscilación posibles corresponden en principio con todas las longitudes de onda posibles. Esto se sigue del mero hecho de modelar el comportamiento del campo como una superposición de ondas a distintas frencuencias, y asumir unas ecuaciones de movimiento a nivel clásico.

    Si hay un oscilador de estos “activado”, es decir oscilando a una determinada frecuencia, se dice que existe una exictación del campo dando lugar a una o varias partículas de esa longitud de onda (o momento lineal según la relación de de-Broglie). Cuando no existen partículas el campo está en su estado vacío. No obstante, en su estado fundamental un oscilador armónico cuántico “desactivado” no tiene energía nula, sino , siendo la frecuencia y la constante de Planck normalizada. Esto es debido al principio de incertidumbre, que impide determinar posición y momento con precisión arbitrariamente grande, lo cual impide por tanto que la energía cinética y potencial en la ecuación de movimiento clásica del oscilador se anulen simultaneamente.

    La energía del vacío del campo es una integral sobre todas las frecuencias de . Esta integral es infinita. No obstante, este valor se puede redefinir arbitrariamente a cero, ya que lo que interesa son valores respecto de él, que nos permitan distinguir lo que conocemos como “vacío”, sin partículas, de excitaciones comportándose como partículas. Conviene por tanto restar ese infinito para poder seguir calculando y obteniendo resultados finitos.

    El efecto Casimir aparece cuando se ponen dos placas muy cerca la una de la otra, de forma que debido a condiciones de contorno geométricas cualquier onda que sobreviva de forma estable en su interior ha de ser necesariamente estacionaria (ha de tener un nodo en cada placa). Está claro que esto hace que en la integral haya longitudes de onda (y por tanto frecuencias) que no contribuyen a ella y, por tanto, el resultado, aunque igualmente infinito, será menor que antes. Como antes hemos asumido la integral sobre todos los como valor cero de energía, ahora el resultado de la energía entre placas es negativo.

    Todo esto vale si no se considera la relatividad general. Para la relatividad general la cosa cambia. Cambia porque en ella ya no está permitido tomar el cero de energía donde uno quiere y separar con ello entre energía positiva y negativa a placer. En la relatividad general la energía positiva es aquella que produce una deformación del espacio-tiempo como conocemos, generando gravitación y cumpliendo el principio de equivalencia, tal y como lo conocemos. La energía negativa se comporta de otra forma y su deformación inducida en el espacio-tiempo es o sería otra (por ejemplo, cierto folklore científico asume que la energía negativa podría ser usada para crear agujeros de gusano).

    Por tanto, la pregunta es si la energía negativa obtenida en un experimento Casimir corresponde también con energía negativa gravitacional. Esto depende del valor en energía gravitacional que nos proporciona la energía del vacío de todos los campos juntos, aquella que por decreto en la teoría cuántica de campos tomamos como cero, pero que ahora debemos considerar. Aquí hay una sutileza respecto de la forma de calcular esta energía, ya que no es exáctamente igual a la integral de de todos los campos, sino que aparecen interacciones entre ellos que proporcionan otras contribuciones también. Pero esto lo vamos a olvidar aquí.

    La pregunta es ¿cómo considerar esa energía y cómo saber cuál es su valor real a efectos gravitatorios? No tenemos otro modo de hacer esto salvo la observación experimental, ya que la respuesta teorica debería venir probablemente de una teoría que unifique cuántica y gravitación a un nivel fundamental. La observación experimental relevante aquí es la cosmología, concrétamente, los datos de distancias de luminosidad de la supernovas Ia, que indican una aceleración de la expansión del espacio. Esta se puede (pero no tiene por qué) deber a una energía del vacío. Los datos indican que esta energía es muy pequeña (“lambda” por constante cosmológica) pero no igual a cero.

    Por tanto, para encontrar concordancia entre la teoría cuántica de campos, la relatividad general y la cosmología, asumimos que nuestro vacío cuántico tiene una energía que no tomamos como cero sino como el valor pequeño . Esto es, si ponemos dos placas muy cercanas, hay longitudes de onda que no pueden existir y que se restan a la energía total del vacío cuántico, por tanto, de . Si la distancia entre las placas es suficiéntemente pequeña, la cantidad de longitudes de onda que no pueden existir es suficiéntemente grande como para que la energía restada a “lambda” de lugar a un valor negativo. Este valor “suficiéntemente pequeño” no es extremadamente pequeño.

    Para conocer este valor vamos a proceder de la siguiente forma. Se trata de un cálculo poco riguroso pero que creo debería valer en órdenes de magnitud. Simplemente consiste en restar a la densidad de energía lambda la densidad de energía que la configuración de dos placas roban al vacío cuántico. Para ello hay que calcular el incremento en la densidad de energía que la configuración de las placas produce entre ellas. Partiendo de la fuerza de Casimir por unidad de area, que atrae a las dos placas:

    siendo la constante de Planck normalizada, la velocidad de la luz en el vacío y la distancia entre las placas, se puede calcular la pérdida de energía entre las placas como un trabajo negativo realizado por el vacío o por la fuerza a distancia :

    Por lo que:

    con la densidad de energía. La densidad energética total será la del vacío menos esta mencionada:

    En unidades de Planck se tiene:

    como se puede leer aquí. Por tanto, con , se tiene:

    Para que sea menor que cero, se tiene que ha de ser menor que longitudes de Planck, que son metros.”

    Publicado por alshain.

    Un saludo 

    Responder
  3. 3
    Iñigo
    el 21 de noviembre del 2010 a las 14:36

    Una cuestion interesante, ciertamente resulta contradictorio primero afirmar que la energia del campo no es nula sino infinita y luego afirmar que a efectos gravitatorios la energia es o nula o muy pequeña, lo cual conduce a una interpretacion bipola, contradictoria, de la energia. Siempre que no se presente el mecanismo por el cual esto se explique razonadamente, solo se tendran un conjunto de reglas ad-hoc para salvar la confrontacion entre RG y Modelo estandar, incluso una costante cosmologica de una naturaleza diferente al de la energia de los campos de la ME que contrareste en alguna medida la energia infinita de estos campos  seria ad-hoc sino es debidamente razonado.

    Responder
  4. 4
    Iñigo
    el 21 de noviembre del 2010 a las 14:45

    Por cierto, veo que el texto que has añadido en el comentario ha sido publicado en http://lastmonolith.blogspot.com/2008/03/el-efecto-casimir-y-la-energa-negativa.html

    Responder
  5. 5
    emilio silvera
    el 22 de noviembre del 2010 a las 8:42

    Estimado amigo:

    En el tema de la energía de vacío y agujeros negros, o, la materia y energía oscura, o, la masa y el Bosón de Higgs, o,…(una lista interminable), estamos aún muy lejos de “saber” y, como usted muy bien sabe, se avanza poco a poco tratando de descubrir los secretos de la Naturaleza y, en Física, la Relatividad Especial y General, junto con la Mecánica Cuántica, el Modelo Estándar (que aunque esté incompleto es una herramienta bastante buena) y otros, van posibilitando nuestros conocimientos.

    Ninguna duda podemos tener de los muchos logros alcanzados y, por supuesto, tampoco, de lo mucho que nos queda por conquistar (semiconductores, espintrónica, fotónica, nanotecnología, fluidos, plasma, y un sin fin de campos cuya lista sería interminable.

    De la energía de vacío o de la singularidad de un agujero negro, no son pocos los físicos que, cuando se toca el tema, prefieren mirar hacia otra parte, ya que, al igual que ocurre con las matemáticas en la teoría de cuerdas, no todos estamos preparados para hacer frente a conceptos que no llegamos a comprender. Sin embargo, está bien continuar y no darse por vencidos, es la única manera de alcanzar algún día, el premio que perseguimos.

    Un cordial saludo.

    Responder
  6. 6
    Contacto
    el 22 de febrero del 2011 a las 2:00

    Muy buen Articulo muchas Gracias por la Información es muy Amplia.

    Responder
.:: Subir ::.

Deja un comentario



Comentario:

XHTML

Subscribe without commenting