Año Internacional de la Astronomía 2009. En España (AIA-IYA2009)

No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas.  Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y m_protón.

La identificación de constantes adimensionales de la naturaleza como α (alfa) y α_G, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala.  La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck).  Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.

Para poner un ejemplo de nuestra ignorancia poco tendríamos que buscar, tenemos a mano miles de millones.

Me acuerdo de León Lederman (premio Nobel de Física) que decía:

“Todos los físicos del mundo, deberían tener un letrero en el lugar más visible de sus casas, para que al mirarlo, les recordara lo que no saben. En el cartel sólo pondría esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina”.

Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck*. Tanta palabrería y numerología no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e^–), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h).

Lo más notable de este número es su dimensionalidad. La velocidad de la luz, c, es bien conocida y su valor es de 299.792.458 m/segundo; la constante de Planck racionalizada, ћ, es h/2π = 1’054589×10 julios segundo; la altura de mi hijo, el peso de mi amigo, etc, todo viene con sus dimensiones.  Pero resulta que cuando uno combina las magnitudes que componen alfa ¡se borran todas las unidades! El 137 está solo: se escribe desnudo a donde va.  Esto quiere decir que los científicos del undécimo planeta de una estrella lejana situada en un sistema solar de la galaxia Andrómeda, aunque utilicen Dios sabe qué unidades para la carga del electrón y la velocidad de la luz y qué versión utilicen para la constante de Planck, también les saldrá el 137.  Es un número puro. No lo inventaron los hombres. Está en la naturaleza, es una de sus constantes naturales, sin dimensiones.

La física se ha devanado los sesos con el 137 durante décadas. Werner Heisember (el que nos regaló el Principio de Incertidumbre en la Mecánica Cuántica), proclamó una vez que todas las fuentes de perplejidad que existen en la mecánica cuántica se secarían si alguien explicara de una vez el 137.

¿Por qué alfa es igual a 1 partido por 137?

Esperemos que algún día aparezca alguien que, con la intuición, el talento y el ingenio de Galileo, Newton o Einstein, nos pueda por fin aclarar el misterioso número y las verdades que encierra. Menos perturbador sería que la relación de todos estos importantes conceptos (e^–, h y c) hubieran resultado ser 1 ó 3 o un múltiplo de pi… pero ¿137?

Arnold Sommerfeld percibió que la velocidad de los electrones en el átomo de hidrógeno es una fracción considerable de la velocidad de la luz, así que había que tratarlos conforme a la teoría de la relatividad. Vio que donde la teoría de Bohr predecía una órbita, la nueva teoría predecía dos muy próximas.

Esto explica el desdoblamiento de las líneas. Al efectuar sus cálculos, Sommerfeld introdujo una “nueva abreviatura” de algunas constantes. Se trataba de 2πe² / hc, que abrevió con la letra griega “α” (alfa). No prestéis atención a la ecuación. Lo interesante es esto: cuando se meten los números conocidos de la carga del electrón, e^–, la constante de Planck, h, y la velocidad de la luz, c, sale α = 1/137.  Otra vez 137 número puro.

Las constantes fundamentales (constantes universales) están referidas a los parámetros que no cambian a lo largo del universo. La carga de un electrón, la velocidad de la luz en el espacio vacío, la constante de Planck, la constante gravitacional, la constante eléctrica y magnética se piensa que son todos ejemplos de constantes fundamentales.

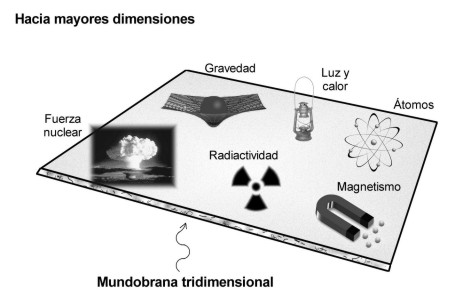
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil.

Las fuerzas fundamentales

Las constantes fundamentales

Unas pueden ser más constantes naturales que otras, pero lo cierto es que, de momento, han servido como herramientas eficaces.

La última lección importante que aprendemos de la manera en que números puros como α (alfa) definen el mundo, es el verdadero significado de que los mundos sean diferentes. El número puro que llamamos constante de estructura fina, e indicamos con α, es como hemos dicho antes, una combinación de e, c y h (el electrón, la velocidad de la luz y la constante de Planck). Inicialmente, podríamos estar tentados a pensar que un mundo en el que la velocidad de la luz fuera más lenta sería un mundo diferente. Pero sería un error. Si e, h y c cambian de modo que los valores que tienen en unidades métricas (o cualesquiera otras) fueran diferentes cuando las buscamos en nuestras tablas de constantes físicas, pero el valor de α permaneciera igual; este nuevo mundo sería observacionalmente indistinguible de nuestro mundo. Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza.

Fue Einstein el que anunció lo que se llamó principio de covariancia: que las leyes de la naturaleza deberían expresarse en una forma que pareciera la misma para todos los observadores, independientemente de dónde estuvieran situados y de cómo se estuvieran moviendo. Cuando trató de desarrollar este principio, Einstein tuvo dificultades; no encontraba la manera de expresarlo con la formulación matemática adecuada. Pidió ayuda a su amigo Marcel Grossmann, matemático, quien sabiendo de las necesidades exactas de Einstein, le envió la copia de una conferencia que dio un tal Riemann, unos sesenta años antes.

Einstein fue muy afortunado, ya que durante la última parte del siglo XIX en Alemania e Italia, matemáticos puros habían estado inmersos en el estudio profundo y detallado de todas las geometrías posibles sobre superficies curvas. Habían desarrollado un lenguaje matemático que automáticamente tenía la propiedad de que toda ecuación poseía una forma que se conservaba cuando las coordenadas que la describían se cambiaban de cualquier manera. Este lenguaje se denominaba cálculo tensorial. Tales cambios de coordenadas equivalen a preguntar qué tipo de ecuación vería alguien que se moviera de una manera diferente.

Einstein se quedó literalmente paralizado al leer la Conferencia de Riemann. Allí, delante de sus propios ojos tenía lo que Riemann denominaba Tensor métrico. Einstein se dio cuenta de que era exactamente lo que necesitaba para expresar de manera precisa y exacta sus ideas. Así  llegó a ser  posible la teoría de la relatividad general.

emilio silvera

[?]