May
15
Números puros adimensionales
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)
Para la XIX Edición del

Hemos hablado aquí con cierta frecuencia del número puro y adimensional, 137. Está relacionado con Alfa (α), la constante de estructura fina. Es un número de la Naturaleza, algo que está ahí y en lo que no hemos intervenido.
Lo más notable de este número es su dimensionalidad. La velocidad de la luz, c, es bien conocida y su valor es de 299.792.458 m/segundo; la constante de Planck racionalizada, ћ, es h/2π = 1’054589×10 julios segundo; la altura de mi hijo, el peso de mi amigo, etc, todo viene con sus dimensiones. Pero resulta que cuando uno combina las magnitudes que componen alfa ¡se borran todas las unidades! El 137 está solo: se escribe desnudo a donde va. Esto quiere decir que los científicos del undécimo planeta de una estrella lejana situada en un sistema solar de la galaxia Andrómeda, aunque utilicen Dios sabe qué unidades para la carga del electrón y la velocidad de la luz y qué versión utilicen para la constante de Planck, también les saldrá el 137. Es un número puro. No lo inventaron los hombres. Está en la naturaleza, es una de sus constantes naturales, sin dimensiones.
La física se ha devanado los sesos con el 137 durante décadas. Werner Heisember (el que nos regaló el Principio de Incertidumbre en la Mecánica Cuántica), proclamó una vez que todas las fuentes de perplejidad que existen en la mecánica cuántica se secarían si alguien explicara de una vez el 137.
¿Por qué alfa es igual a 1 partido por 137?
Esperemos que algún día aparezca alguien que, con la intuición, el talento y el ingenio de Galileo, Newton o Einstein, Rieman o Ramanujan nos pueda por fin aclarar el misterioso número y las verdades que encierra. Menos perturbador sería que la relación de todos estos importantes conceptos (e–, h y c) hubieran resultado ser 1 ó 3 o un múltiplo de pi… pero ¿137?
Arnold Sommerfeld percibió que la velocidad de los electrones en el átomo de hidrógeno es una fracción considerable de la velocidad de la luz, así que había que tratarlos conforme a la teoría de la relatividad. Vio que donde la teoría de Bohr predecía una órbita, la nueva teoría predecía dos muy próximas.
Esto explica el desdoblamiento de las líneas. Al efectuar sus cálculos, Sommerfeld introdujo una “nueva abreviatura” de algunas constantes. Se trataba de 2πe2 / hc, que abrevió con la letra griega “α” (alfa). No prestéis atención a la ecuación. Lo interesante es esto: cuando se meten los números conocidos de la carga del electrón, e–, la constante de Planck, h, y la velocidad de la luz, c, sale α = 1/137. Otra vez 137 número puro.
Las constantes fundamentales (constantes universales) están referidas a los parámetros que no cambian a lo largo del universo. La carga de un electrón, la velocidad de la luz en el espacio vacío, la constante de Planck, la constante gravitacional, la constante eléctrica y magnética se piensa que son todos ejemplos de constantes fundamentales.
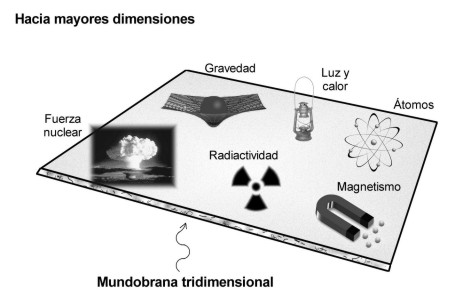
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil.
La última lección importante que aprendemos de la manera en que números puros como α (alfa) definen el mundo, es el verdadero significado de que los mundos sean diferentes. El número puro que llamamos constante de estructura fina, e indicamos con α, es como hemos dicho antes, una combinación de e, c y h (el electrón, la velocidad de la luz y la constante de Planck). Inicialmente, podríamos estar tentados a pensar que un mundo en el que la velocidad de la luz fuera más lenta sería un mundo diferente. Pero sería un error. Si e, h y c cambian de modo que los valores que tienen en unidades métricas (o cualesquiera otras) fueran diferentes cuando las buscamos en nuestras tablas de constantes físicas, pero el valor de α permaneciera igual; este nuevo mundo sería observacionalmente indistinguible de nuestro mundo. Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza.
Ahora sabemos que las fuerzas de la naturaleza, la fuerza nuclear fuerte, la fuerza nuclear débil, el electromagnetismo y la gravedad, no son tan diferentes como parece a primera vista. Parecen tener intensidades muy diferentes y actuar sobre partículas elementales diferentes. Pero eso es ilusorio, es la sensación creada por nuestra necesidad de habitar en un lugar del universo donde la temperatura es más bien baja y, es así, como se manifiestan las fuerzas de la naturaleza que, en dicha temperatura permite la existencia de átomos y moléculas.
Conforme la temperatura aumenta y las partículas elementales de materia colisionan entre sí a energías cada vez más altas, las fuerzas separadas que gobiernan nuestro mundo de baja temperatura, se hacen más parecidas. La fuerza fuerte se debilita, la fuerza débil aumenta y fortalece. Aparecen nuevas partículas a medida que se alcanzan temperaturas más elevadas y consiguen producir interacciones entre las familias separadas de partículas que a temperaturas bajas, parecen estar aisladas entre sí. Poco a poco, a medida que nos acercamos a esas inimaginables condiciones de temperatura “última” que Max Planck encontró definida por las cuatro constantes de la naturaleza, G, K, c, h, esperamos que las diferencias entre las fuerzas naturales se vayan borrando completamente para finalmente quedar unificadas en una única fuerza como, por otra parte, se cree que fue al principio de todo, cuando en el Big Bang, el proceso ocurrió al contrario. Había una increíble temperatura, un plasma primordial lo invadía todo y se expansionaba, naciendo el tiempo y el espacio cuando reinaba la simetría total y una sola fuerza lo regía todo. El universo continuó su expansión y comenzó a enfriarse, la simetría se rompió y lo que era una sola fuerza se dividió en las cuatro que ahora conocemos. Previamente, a partir del plasma, al bajar la temperatura, surgieron los quarks que se juntaron para formar protones y neutrones que, a su vez, se juntaron para formar núcleos que, al ser rodeados por los electrones atraídos por la carga positiva de los núcleos, formaron los átomos, que se unieron para formar moléculas, que se juntaron para formar la materia, que más tarde, dio lugar al nacimiento de las primeras estrellas y galaxias con sus variedades de objetos estelares, planetas, satélites, cometas, meteoritos.
Pero, volvamos a la Física. De entre todos los que intentaron descubrir los misterios del 137, me detendré un momento en Arthur Eddington, uno de los más grandes astrofísicos del siglo XX, combinación de lo más profundo y lo fantástico. Más que cualquier otra figura moderna es el responsable de poner en marcha los inacabables intentos de explicar las constantes de la naturaleza por proezas de numerología pura. Él también advirtió un aspecto nuevo y espectacular de las constantes de la naturaleza.
Cuando los físicos empezaron a apreciar el papel de las constantes en el dominio cuántico y explotar la nueva teoría de la gravedad de Einstein para describir el universo en conjunto, las circunstancias eran las adecuadas para que alguien tratara de casarlas.
Así entró en escena Arthur Stanley Eddington: un extraordinario científico que había sido el primero en descubrir cómo se alimentaban las estrellas a partir de reacciones nucleares. También hizo importantes contribuciones a nuestra comprensión de las galaxias, escribió la primera exposición sistemática de la teoría de la relatividad general de Einstein y fue el responsable de la expedición que durante un eclipse de Sol, pudo confirmar con certeza la predicción de la relatividad general que debería desviar la luz estelar que venía hacia la Tierra en aproximadamente 1’75 segundos de arco cuando pasaba cerca de la superficie solar, cuyo espacio estaría curvado debido a la gravedad generada por la masa del Sol. En aquella expedición, el equipo de Eddington hizo una exitosa medición del fenómeno desde la isla Príncipe, que confirmó que Einstein tenía razón y que su teoría predecía de manera exacta la medida de curvatura del espacio en función de la masa del objeto estelar que genera la gravitación distorsionando el espaciotiempo a su alrededor.
Entre los números que Eddington consideraba de importancia primordial estaba al que ahora conocemos como número de Eddington, que es igual al número de protones en el universo visible. Eddington calculó (a mano) este número con enorme precisión en un crucero trasatlántico, concluyendo con esta memorable afirmación:
“Creo que en el Universo hay 15.747.724.136.275.002.577.605.653.961.181.555.468.044.717.914.527.116.709.366.231.425.076.
.185.631.031.296 protones y el mismo número de electrones”.
Este número enorme, normalmente escrito NEdd, es aproximadamente igual a 1080. Lo que atrajo la atención de Eddington hacia él era el hecho de que debe ser un número entero, y por eso en principio puede ser calculado exactamente.
Durante la década de 1.920, cuando Eddington empezó su búsqueda para explicar las constantes de la naturaleza, no se conocían bien las fuerzas débil y fuerte de la naturaleza. Las únicas constantes dimensionales de la física que sí se conocían e interpretaban con confianza eran las que definían la gravedad y las fuerzas electromagnéticas. Eddington las dispuso en tres puros números adimensionales. Utilizando los valores experimentales de la época, tomó la razón entre las masas del protón y del electrón:
mpr/me ≈ 1840
La inversa de la constante de estructura fina
2πhc/e2 ≈ 137
Y la razón entre la fuerza gravitatoria y la fuerza electromagnética entre un electrón y un protón,
e2/Gmpr me ≈ 1040
A estas añadió su número cosmológico, NEdd ≈ 1080. A estos cuatro números los llamó “las constantes últimas”, y la explicación de sus valores era el mayor desafío de la ciencia teórica:
“¿Son estas cuatro constantes irreducibles, o una unificación posterior de la física que pueda demostrar que una o todas ellas podrían ser prescindibles? ¿Podrían haber sido diferentes de lo que realmente son?… Surge la pregunta de si las razones anteriores pueden ser asignadas arbitrariamente o si son inevitables. En el primer caso, sólo podemos aprender sus valores por medida; en el segundo caso es posible encontrarlos por la teoría… Creo que ahora domina ampliamente la opinión de que las (cuatro anteriores) constantes… no son arbitrarias, sino que finalmente se les encontrará una explicación teórica; aunque también he oído expresar lo contrario.”
Siguiendo con su especulación Eddington pensaba que el número de constantes inexplicadas era un indicio útil del hueco que había que cerrar antes de que se descubriese una teoría verdaderamente unificada de todas las fuerzas de la naturaleza. En cuanto a si esta teoría final contenía una constante o ninguna, tendríamos que esperar y ver:
“Nuestro conocimiento actual de 4 constantes en lugar de 1 indica meramente la cantidad de unificación de teoría que aún queda por conseguir. Quizá resulte que la constante que permanezca no sea arbitraria, pero de eso no tengo conocimiento.”
Eddington, como Max Planck, Einstein y Galileo, y Newton antes que ellos, era simplemente un adelantado a su tiempo; comprendía y veía cosas que sus coetáneos no podían percibir.
El mayor misterio que rodea a los valores de las constantes de la naturaleza es sin duda la ubicuidad de algunos números enormes que aparecen en una variedad de consideraciones aparentemente inconexas. El número de Eddington es un ejemplo notable. El número total de protones que hay dentro del alcance del universo observable esta próximo al número
1080
Si preguntamos ahora por la razón entre las intensidades de las fuerzas electromagnéticas y gravitatoria entre dos protones, la respuesta no depende de su separación, sino que es aproximadamente igual a
1040
En un misterio. Es bastante habitual que los números puros que incluyen las constantes de la naturaleza difieran de 1 en un factor del orden de 102, ¡pero 1040, y su cuadrado 1080, es rarísimo! Y esto no es todo. Si seguimos a Max Planck y calculamos en valor estimado para la “acción” del universo observable en unidades fundamentales de Planck para la acción, obtenemos.
10120
Ya hemos visto que Eddington se inclinaba a relacionar el número de partículas del universo observable con alguna cantidad que incluyera la constante cosmológica. Esta cantidad ha tenido una historia muy tranquila desde esa época, reemergiendo ocasionalmente cuando los cosmólogos teóricos necesitan encontrar una manera de acomodar nuevas observaciones incómodas. Recientemente se ha repetido este escenario. Nuevas observaciones de alcance y precisión sin precedentes, posibilitadas por el telescopio espacial Hubble trabajando en cooperación con telescopios sensibles en tierra, han detectado supernovas en galaxias muy lejanas. Su pauta de brillo y atenuación característica permite deducir su distancia a partir de su brillo aparente. Y, sorprendentemente, resulta que están alejándose de nosotros mucho más rápido de lo que cualquiera esperaba. La expansión del universo ha pasado de ser un estado de deceleración a uno de aceleración. Estas observaciones implican la existencia de una constante cosmológica positiva (Λ+). Si expresamos su valor numérico como número pero adimensional medido en unidades del cuadrado de la longitud de Planck, entonces obtenemos un número muy próximo a
10-120
Nunca se ha encontrado un número más pequeño en una investigación física real.
¿Qué vamos a hacer con todos estos grandes números? ¿Hay algo cósmicamente significativo en 1040 y sus cuadrados y cubos?
La aparición de algunos de estos grandes números ha sido una fuente de sorpresas desde que fue advertida por vez primera por Hermann Weyl en 1.919. Eddington había tratado de construir una teoría que hiciera comprensible su aparición, pero no logró convencer a un número significativo de cosmólogos de que estaba en la vía correcta. Pero sí convenció a la gente de que había algo que necesitaba explicación. De forma inesperada, fue precisamente uno de sus famosos vecinos de Cambridge quien escribió a la revista Nature la carta que consiguió avivar el interés por el problema con una idea que sigue siendo una posibilidad viable incluso hoy.
Paul Dirac ocupó la cátedra lucaciana de matemáticas en Cambridge durante parte del tiempo en que Eddington estuvo viviendo en los observatorios. Las historias que se cuentan de Paul Dirac dejan muy claro que era un tipo con un carácter peculiar, y ejercía de matemático las 24 h. del día. Se pudo saber que su inesperada incursión en los grandes números fue escrita durante su viaje de novios (Luna de miel), en febrero de 1.937.
Aunque no muy convencido de las explicaciones de Eddington, escribió que era muy poco probable que números adimensionales muy grandes, que toman valores como 1040 y 1080, sean accidentes independientes y no relacionados: debe existir alguna fórmula matemática no descubierta que liga las cantidades implicadas. Deben ser consecuencias más que coincidencias.
En otro próximo trabajo hablaremos de los números de Dirac.






















 Totales: 83.335.506
Totales: 83.335.506 Conectados: 5
Conectados: 5























el 28 de septiembre del 2011 a las 17:49
Un cálculo un poco atrabiliario:
10^40 representa la presión oscura sobre la unidad de superficie de cualquier elemento = fuerza fuerte
10^40 equivalente a densidad oscura sobre superficie unidad = Fuerza fuerte calculada según G=6,67· 10^-11 (escala protón atomo)
Los elementos aumentan según espacio de forma cuadrática (10^40)^2 = 10^80 = nº de protones apantallados por la presión oscura (que decrece en proporción) en espacio creciente.