May
1
¿Quién fue Riemann?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (14)
Comments (14)
Arthur C. Clarke nos dijo: “Magia es cualquier tecnología suficientemente avanzada”

Según Clarke, todo esto es magia…
Pero también es magia el hecho de que en cualquier tiempo y lugar, de manera inesperada, aparezca una persona dotada de condiciones especiales que le permiten ver estructuras complejas matemáticas que hacen posible que la humanidad avance considerablemente a través de esos nuevos conceptos que nos permiten entrar en espacios antes cerrados, ampliando el horizonte de nuestro saber.
Recordémos aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.

Georg Friedrich Bernhard Riemann
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
¿Podría ser nuestro universo una membrana flotando en un espacio de más dimensiones, que se rompe muchas veces en un universo circundante? Según una rama de la teoría de las cuerdas llamada braneword, hay una gran cantidad de dimensiones extra de espacio, y aunque la gravedad puede llegar a salir, nosotros estamos confinados a nuestro propio universo “brana”, con sólo tres dimensiones.
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis. Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.

Hannover, Alemania
A la edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Portada de la segunda edición del “Essai sur la Théorie des Nombres” de A. M. Legendre (1798)
Cuando el director le preguntó: “¿hasta dónde has leído?”, el joven Riemann respondió: “este es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente y, en algún caso, hizo puntualizaciones que mejoraban el enunciado del libro y sus respuestas.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

Así era la Universidad donde estudió Riemann
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).

Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.
No podemos ver un hipercubo porque estamos “encerrados” en tres dimensiones, por lo que solo podemos ver la sombra de lo que seria un hipercubo. Se parece a dos cubos anidados, con todos los vértices conectados por líneas. Pero en el teseracto real de cuatro dimensiones todas las líneas tendrían la misma longitud y todos los ángulos serían ángulos rectos.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
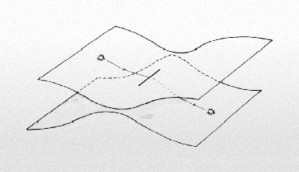
Gráfico: Un corte de Riemann, con dos hojas conectadas a lo largo de una línea. Si caminamos alrededor del corte, permanecemos dentro del mismo espacio. Pero si atravesamos el corte, pasamos de una hoja a la continua. Esta es una superficie múltiplemente conexa.
Riemann desarrolló su teoría de dimensiones más altas.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.
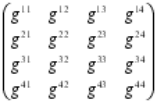
El tensor de Riemann contiene toda la información necesaria para poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico tiene diez números independientes).
De hecho, en las nuevas teorías de supercuerdas, planteadas en diez y veintiséis dimensiones, tendríamos que hablar del super tensor métrico de Riemann y de cientos de componentes.
Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Topológicamente hablando, el dibujo adjunto es equivalente a lo que sería un agujero de gusano con boca de entrada y de salida en regiones que nos llevarían a otro tiempo. Riemann anticipó otro desarrollo de la física; fue uno de los primeros en discutir espacios múltiples y conexos, o agujeros de gusano.
Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
Pero volvamos al trabajo de Riemann. Su propósito era introducir un nuevo objeto en las matemáticas que le capacitase para describir todas las superficies, por complicadas que fueran. Ésto le condujo inevitablemente a reintroducir el concepto de campo de Faraday.
El campo de Faraday, recordémoslo, era como un campo de granjero que ocupa una región de un espacio bidimensional. El campo de Faraday ocupa una región de un espacio tridimensional; a cualquier punto del espacio le asignamos una colección de números que describe la fuerza eléctrica o magnética en dicho punto. La idea de Riemann consistía en introducir una colección de números en cada punto del espacio que descubriera cuánto estaba torcido o curvado.
Por ejemplo, para una superficie bidimensional ordinaria, Riemann introdujo una colección de tres números en cada punto que describe completamente la curvatura de dicha superficie. Riemann descubrió que en cuatro dimensiones espaciales se necesita una colección de diez números en cada punto del espacio para describir sus propiedades. Por muy retorcido o distorsionado que esté el espacio, esta colección de diez números en cada punto es suficiente para codificar toda la información sobre dicho espacio. Hoy, esta colección de números se denomina el Tensor métrico de Riemann. Hablando crudamente, cuanto mayor es el valor del tensor métrico, mayor es el arrugamiento de la superficie, digamos de una hoja de papel, y el tensor métrico nos da un medio sencillo para medir la curvatura en cada punto. Si alisamos completamente la hoja arrugada, entonces recuperamos la fórmula de Pitágoras.
TEOREMA DE PITÁGORAS

En todo triángulo Rectángulo la suma de las áreas que forman los cuadrados de los catetos es igual al área del cuadrado formado por la hipotenusa (hay cosas que nunca cambian). De hecho, esta fórmula está presente en la mayoría de las construcciones de todos los tiempos. Pero volvamos a Riemann.
El tensor métrico de Riemann le permitió erigir un potente aparato para describir espacios de cualquier dimensión con curvatura arbitraría. Para su sorpresa, encontró que todos estos espacios están bien definidos y son autoconsistentes. Previamente, se pensaba que aparecerían terribles contradicciones al investigar el mundo prohibido de dimensiones más altas. Riemann no encontró ninguna. De hecho, resultaba casi trivial extender su trabajo a un espacio N-dimensional. El tensor métrico se parecía ahora a un tablero de ajedrez de N x N casillas.
El tensor de Riemann contiene toda la información necesaria para poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico tiene diez números independientes).

De hecho, en las nuevas teorías de supercuerdas, planteadas en diez y veintiséis dimensiones, tendríamos que hablar del supertensor métrico de Riemann y de cientos de componentes.

De la lección de Riemann se deduce que en espacios multidimensionales se crea el principio de que el espacio múltiple (de más dimensiones) unifica las leyes de la naturaleza encajándolas en el tensor métrico como piezas de un rompecabezas N-dimensional. Riemann anticipó otro desarrollo de la física; fue uno de los primeros en discutir espacios múltiples y conexos, o agujeros de gusano.

El legado de Riemann (a pesar de su muerte prematura) fue extenso y en general muy valioso. En 1958, anunció incluso que finalmente había logrado una descripción unificada de la luz y la electricidad. Escribió: “Estoy completamente convencido de que mi teoría es la correcta, y de que en pocos años será reconocida como tal”. Aunque su tensor métrico le proporcionó un medio poderoso de describir cualquier espacio curvo en cualquier dimensión, él no conocía las ecuaciones exactas a que obedecía el tensor métrico; es decir, no sabía quçe es lo que hacía que la hoja se arrugase, eso lo vio seis décadas más tarde Einstein que se dio cuenta de que, en presencia de grandes masas, tales como planetas o estrellas – entre otros –, el espacio se “arruga” o “distorsiona”, se curva. Sin embargo Einstein sabía el origen de las arrugas y le faltaba el tensor métrico que, finalmente, le permitió legar al mundo su magnifica teoría.
El trabajo de Riemann, al utilizar el espacio multidimensional, logró simplificar las leyes de la naturaleza, es decir, para él, la electricidad y el magnetismo y también la gravedad eran simplemente los efectos causados por el arrugamiento o distorsión del hiperespacio.
Su asombroso trabajo (que no terminó), fue rematado por dos genios como Maxwell (electricidad y magnetismo) y Einstein (gravedad).
Publica emilio silvera a partir de varias fuentes.
















 Totales: 75.497.219
Totales: 75.497.219 Conectados: 31
Conectados: 31























el 18 de octubre del 2011 a las 23:15
Amigo mio; Cuan gratificante resulta leer tus artículos, llenos de informaciones que nos ayudan a hacernos cada día mas conocedores y amigos de esos capítulos un poco olvidados y que no muchos saben.
La lectura y el conocimiento nos enriquece y las aportaciones como la tuya, marcan ese norte, si fue por mi, ya te habría entregado tu merecido reconocimiento. Has de seguir por ese camino, pues al igual que las estrellas, tu destino ya está definido, aunque el tuyo claramente es otro, no terminaras como agujero negro ni como enana blanca, sino seguiras entregando y deleitanto a miles de seguidores con mas y mas cultura.
Saludos cósmicos desde “Univeros Para Todos”
Abdel Majluf
el 19 de octubre del 2011 a las 5:36
Amigo mío, se agradecen tus palabras aunque sólo sea por el reconocimiento a una labor continuada y diversa en la que, el principal objetivo es, como bien dices, el de llevar información a otros en relación a cuestiones que no siempre están al alcance de todos, y, de esa manera, si consigo que algunos se enteren de lo que no sabían, o, les intereso en temas como la Astronomía, la Física o la complejidad de la vida…, ya tenemos uno más en el grupo de los que quieren saber.
Está claro que, al igual que el tiempo siempre nos alcanza y termina venciéndonos, de la misma manera, por mucho tiempo que estemos aquí, nunca alcanzaremos los conocimientos que incansables perseguimos, nadie puede saberlo todo. Sin embargo, el conseguir no estar en la ignorancia absoluta, el saber algo sobre el mundo que te rodea, el tener una idea aproximada de como funciona el mundo, el vislumbrar (aunque sólo sea la sombra), lo que nuestra mente es…, reconforta y te hace un poco más consciente de Ser, y, cuando se llega a ese límite, se quiere llevar a los demás a ese lugar en el que tú estas para compartir con ellos ese poco del saber del mundo.
¿No es una maravilla en sí misma que, la historia de la vida, desde sus inicios más tempranos hasta el conjunto de microbios, hongos, plantas y animales, seres humanos incluidos, que envuelve hoy en día la Tierra en una pintoresca red de vida palpitante, nos permitiera llegar a las estrellas y a las galaxias lejanas? Y, ¿qué decir de las biotecnologías y de la posible vida inteligente fuera de nuestro planeta? ¿Cómo vamos a dejar de intentar saber sobre esos mundos remotos de exótica y fascinante belleza? ¿Cómo dejar de interesarnos por las estrellas y lo que suponen para el cambio de fase en la materia primaria?
Son tantas las cosas que nos pueden llegar a interesar que, nuestra innata curiosidad nunca se verá saciada, y, ese germen que nos empuja a querer saber (menos mal que es así), siempre estará con nosotros.
Precisamente por eso tú estás ahora aquí, y, dices en alta voz que el lugar te gusta y que te fascinan algunas de las cosas que aquí puedes encontrar y, de la misma manera, por mi parte, quedo encantado de visitar tu propio sitio que llamas “Universo para Todos”. Cuando entramos en esa dinámica de querer saber…,¿quién puede pararnos?
Un abrazo amigo.
el 19 de octubre del 2011 a las 5:06
Sabes hacer ciencia con arte y arte con ciencia, su lírica, asombra. ¿Y para que sirve esto? Seguro le preguntarían a Riemann; bueno, si no sirve para nada, al menos hará mas entendible la geometría euclidiana. Es que la comparación, es una de la forma que usa la mente humana para mejorar su aprendizaje, en los niños un mayor porciento… Es decir, si la geometría rimenniana no sirviera más que como un juego abstracto, aun así, tendría valor metodológico… Merito de supergenio el del kazajo Lovachevski, que lejos de la civilizada y culta Europa; y en contra de todos los bajos intereses, hizo casi lo mismo y si no hubiera nacido un Gauss o un Riemann, no hubiera importado, eso hubiera bastado para que cualquiera después prolongando la idea lo hubiera construido todo. ‘Pese a miles de dificultades, mi amigo, sigo trabajando: ¿Y para que sirve esto?…
el 19 de octubre del 2011 a las 5:51
Amigo Tom:
Me ha alegrado que traigas aquí al kazajo Lobachevski, el cual, como bien dices, tampoco se quedó atrás en sus aportaciones en este campo y, como el mismo Riemann, tiene un mérito indudable en el avance de las matemátiocas y la geometría.
Dejemoslé aquí un pequeño homenaje:
“Nikolái Ivánovich Lobachevski (en caracteres cirílicos: Никола́й Ива́нович Лобаче́вский) (1 de diciembre de 1792 – 24 de febrero de 1856) fue un matemático ruso del siglo XIX.
Entre sus principales logros se encuentra la demostración de varias conjeturas relacionadas con el cálculo tensorial aplicados a vectores en el espacio de Hilbert.
Fue uno de los primeros matemáticos que aplicó un tratamiento crítico a los postulados fundamentales de la geometría euclidiana.
Nació en Nizhni Nóvgorod y estudió en la Universidad de Kazán. Enseñó en Kazán desde 1812 hasta 1846, y llegó a ser profesor de matemáticas en 1823.
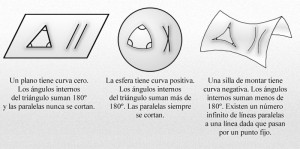
Con independencia del húngaro János Bolyai y del alemán Carl Friedrich Gauss, Lobachevski descubrió un sistema de geometría no euclidiana. Antes de Lobachesvski, los matemáticos intentaban deducir el quinto postulado de Euclides a partir de los otros axiomas; sin embargo, Lobachevsky se dedicó a desarrollar una geometría en la cual el quinto postulado puede no ser cierto o, mejor dicho, no ser válido. Para esto, entre otras cuestiones propuso un sistema geométrico basado en la hipótesis del ángulo agudo, según la cual, en un plano, por un punto fijo pasan al menos 2 paralelas a una recta -en realidad tal solución da noción de la existencia de triángulos curvos.
Entre sus obras destacan Sobre los principios de la geometría (1829) y Geometría imaginaria (1835).
Murió en Kazán en 1856.”
Dices que, a pesar de miles de dificultades sigues trabajando y, preguntas para qué. La respuesta es sencilla, si así lo haces es por el simple hecho de que eres físico, lo que llevas dentro, ese motor en forma de mente, no deja de pensar y las ideas que generas te llevan a seguir para satisfacer tu propia curiosidad y, por otra parte, como bien sabes, todo es fruto de la causalidad, y, si trabajas…, la paga llegará más tarde o más temprano.
Sigue por ese camino amigo mío, de otra manera, sería rendirse, y, eso, es lo último que uno tiene que hacer y sólo cuando nos quede el poco aliento del final del que nadie puede huir.
Un saludo cordial.
el 21 de octubre del 2011 a las 1:18
Así pues me asombra como los matemáticos de aquella época no necesitaban de graficadores. Los tensores son relativamente sencillos de usar aunque a veces uno se pierde y no sabe en donde esta parado. Siempre he querido filosofar sobre esta álgebra tensorial, ademas se su extenso uso. Y uno puede hablar se distintos tenores como el tensor de inercia o el tensor Levi-Civita. Estos también son útiles en las transformaciones de Lorentz. En fin las matemáticas hablan por su cuenta y no la inventan los matemáticos. Historias como esta me hacen recordar la historia de los cuaterniones de Hamilton, otra muy curiosa.
el 21 de octubre del 2011 a las 6:13
¡Ay! amigo Riesling, qué verdad es lo que dices, las matemáticas tienen sus propios caminos y nosotros nos topamos con ellos por casualidad. Como Riemann, Ramanujan, Hamilton, Gauss, Cantor, Euler, …y tantos otros antes y después, nos hemos asombrado de sus logros y, creo que en ellos, la Naturaleza dejó ese algo especial que les hacía ver y comprender las matemáticas sobre todo lo demás, y, de la misma manera que a otros se les dá bien la literatura, la música o la pintura, ellos fueron elegidos para ser matemáticos.
Las matemáticas, como un lenguaje especial, son las que nos pueden contar aquellas cosas en las que las palabras no saben o no pueden describir la realidad compleja del mundo.
Un saludo cordial.
el 2 de mayo del 2012 a las 2:09
¡Hola, Emilio!
Difícilmente, un hombre contemporáneo, concluiría que (luego de ser puesto frente a alguna de las maravillas tecnológicas de nuestro tiempo) está en presencia de algo mágico, en razón de que si tiene un mínimo de instrucción deberá reconocer que, con tiempo y esfuerzo, puede él mismo llegar a comprender los fundamentos de esa forma de “magia”.
Otra cosa, sería si ese hombre fuera algún integrante de una tribu perdida del Congo u otro lugar remoto, totalmente huérfano de todo conocimiento tecnológico y con un coeficiente de inteligencia asimismo precario.
Si no me equivoco, fue Carl Sagan quien reivindicó las palabras del extinto A.C.Clarke diciendo que si algún día entráramos en contacto efectivo con alguna civilización extraterrestre, cualquier logro procedente de ellos nos parecería indistinguible de la magia. Pero aún en este caso, creo que Sagan se equivocó puesto que teniendo en cuenta nuestro bagage científico-tecnológico (aunque rudimentario y risible comparado con una hipotética civilización extraterrestre avanzada) a ninguno de nosotros escapa que, con seguridad e inevitablemente, hay muchas depuraciones sucesivas fruto del esfuerzo alienígeno que dan como resultado final a esa maravilla aparente. Aquello que allí afuera “otros” han logrado, nosotros aquí también algún dia.
Atentamente…
Adolfo
el 2 de mayo del 2012 a las 6:14
Que no te quepa la menor duda amigo, nosotros, al igual que cualquier otro fuera de nuestro mundo, alcanzaremos esos conocimientos “mágicos” a los que aludes. Claro que, no será tanta magia como esfuerzo el haber podido llegar hasta ellos.
Tiempo, estudio y mucho trabajo de observación y experimentación…y, ahí estaremos. De todas las maneras, soy del parecer de que, no necesariamente unos alienigenas enidos de mundos ignotos, estarían necesariamente por delante de nosotros en el saber de los secretos de la Naturaleza, ya que, para cuando ese encuentro llegue a ocurrir, también nosotos habremos evolucionado hasta equiparanos a cualquier raza o especie que nos pueda visitar y, si me apuras mucho, los visitantes podríamos ser nosotos.
Un abrazo amigo.
el 2 de mayo del 2012 a las 2:59
¡Hola, Emilio!
Si el Hombre es producto del quehacer de un Dios, entonces Dios ha sabido invertir en nosotros los logros de una tecnología increiblemente avanzada, para dar a luz ese órgano que es capaz de todo lo bueno y todo lo malo de lo que somos capaces, nuestro cerebro, asiento de nuestra conciencia. No asimilaré (aunque quizá, tú si, lo quieras) a la conciencia, el concepto de magia, puesto que (y puede que Dios me parta con un rayo al salir de mi casa, dada su omnisciencia) tengo la seguridad de que algún día seremos tan poderosos como Él; después de todo, nos creó a su imagen y semejanza… ¿no?
Atentamente…
Adolfo
el 2 de mayo del 2012 a las 6:24
Está claro que, nuestras conciencias no son el producto de magía alguna ni la podemos así considerar. Se trata de un ente muy real que, simplemente evoluciona y está perfectamente conformada para llegar a un alto niel del entendimiento del mundo que nos rodea y, en consecuencia de toda la Naturaleza. Ceo también que, ningún Dios ha tenido nada que ver con esto y que, nosotros, nunca seremos dioses, simplemente llegaremos a ser personas muy avanzadas si el transcurrir del mundo (y del Unierso) lo permite.
Hemos tenido la suerte de poseer un cerebro muy especial en el que, una “mente inmaterial” surge po encima de todo lo demás y se eleva hasta alturas hasta hace bien poco inconcebibles, y, eso no es magia, es evolución. Como he dicho muchas veces, el Univeso evoluciona y nosotros con él, ya que, siendo uno de sus componentes (el que piensa), así debe ser.
Y, sí, llegaemos a ser muy poderosos y podremos manejar energías que ahora son impensables, podremos teraformar mundos para instalarnos en ellos y, podremos…tántas cosas. Sin embargo, dioses nunca seremos, aunque si nos pudieran visitar nuestros ancestros del pasado y pudieran comntemplar de lo que hemos llegado a ser capaces, sí que lo creerían.
Siempre seremos “simplemente” Humanos que tienen aquellas condiciones físicas y mentales para llegar…muy lejos en el conocimiento de la Naturaleza que guarda todas aquellas respuestas que necesitamos conocer.
Un abrazo amigo.
el 15 de mayo del 2012 a las 17:58
todo tu articulo me parecio muy similar a unas paginas del libro hiperespacio de Michio Kaku donde se hace referencia al tensor metrico de Riemann y sus aportaciones a las matematicas. Got you! fool me once shame on me, fool me twice shame on you!
el 16 de mayo del 2012 a las 5:38
Hola, Pablo;
Tienes buen ojo amigo, una página como esta se nutre de muchas fuentes y, desde luego, esas fuentes están situadas en los templos del saber que, generalmente (aparte de las Universidades) están en los libros, artículos y noticias relacionadas con la Ciencia y sus distintas disciplinas.
Un saludo cordial.
el 4 de agosto del 2013 a las 2:47
¡Hola, Kasha!
Si mantienes abierta la puerta de tu casa, lo lógico es pensar que estás ofreciéndola a todo aquel que quiera entrar para descansar un poco y tomar aliento en el largo recorrido que la vida nos obliga a efectuar. Así que, un alto en el camino en un lugar donde te acojan con agrado y, además, te ofrezcan buena información, donde te cuenten cosas que no sabías, un lugar en el que te digan como funciona la Ciencia y te ofrezcan pasajes de lo que pasa en el Universo y cómo funciona ma Física… Si eres curioso, si deseas saber, lo recibirás con agrado.
Eso es lo que pasa aquí y lo que se encuentra el viajero que entra (no pocas veces por azar), para hallar, es posible que algo que no esperaba y, no pocas veces volverá en busca de más información valiosa de cómo nacen, viven y mueren las estrellas, o de qué son las partículas elementales y el por qué se comportan como lo hacen.
Venga cada vez que quiera en la seguridad de que será bien acogido.
Un saludo cordial.