¿Es la Física una mercancía?

Leyendo el comentario de nuestro contertulio Tom Wood, termina uno la lectura con la impresión de que, al fin y al cabo, el esfuerzo de los físicos no sirve para mucho aparte de descubrir, de vez en cuando, alguna nueva partícula para añadir al Modelo y, que más o menos accidentalmente, se ha llegado a una descripción que representa adecuadamente todo lo que conocemos hasta el presente y que ha sido aportado a eso que se ha dado en llamar “modelo estándar de la Fisica de Partículas en el que se recogen tres de las cuatro fuerzas y se explican las propuedades de las partícuals y sus interacciones pero, a pesar de todo, deja algunos cabos sueltos.

Después de un buen rato, he tenido que dejar de buscar la situación del gravitón en este cuadro, y, de pronto caí en la cuanta de que, en el Modelo estándar, sólo se incluyen tres de las cuatro fuerzas, por lo tanto, nunca podría encontrar aquí el Gravitón.

Pero, realmente ¿se podrían concluir cosas nuevas de él, algo que no hubiera sido posible conocer por adelantado, una predicción de algo realmente nuevo? Hay veces en las que, toda la fanfarria y parafernalia con la que se presentan algunos “logros”, nos pueden llevar a pensar que, se está tratando de vender algo y, en alguna ocasión, ¡algo que no se tiene!

Las partículas que tenemos hasta ahora empiezan siendo de masa nula. Luego, añadimos una partícula con espín 0, la partícula de Higgs, que hace todo el trabajo pesado. Todas las partículas –Bosones gauge, fermiones y, desde luego, la propia Higgs- deben su masa a la interacción con la Higgs. Hasta hace muy poco tiempo nunca se había detectado la Higgs y, para evitarlo, se construyó esa inmensa máquina de muchos miles de millones de dolores, ya que, todos decían que, el “Campo de Higgs” se sentía por todas partes y, si la partícula de Higgs no estuviera ahí, nuestro modelo sería tan simétrico que todas las partículas parecerían iguales; habría demasiada poca diferenciación. Para que las partículas obtengan sus masas, las simetrías deben ser suficientemente reducidas.

Esto tiene que ver con la conservación de la helicidad, el espín a lo largo del eje paralelo a su movimiento, pero los detalles son demasiado matemáticos y aquí queremos evitar las ecuaciones que no todos comprendemos. Lo que es importante recordar es que todas las partículas deben su masa a las interacciones con el Campo de Higgs.

Pero no es sólo la masa, otras estructuras también surgen en la teoría debido a las muchas formas en la que los fermiones interaccionan con el Campo de Higgs. Esto significa que las masas serán todas diferentes. Además, habiendo tres generaciones, hay sitio suficiente para interacciones que violen la simetría PC, de manera que en el Modelo también se explican las extrañas desintegraciones de la partícula K_L en dos piones.

Todos hemos podido ver alguna Tabla de partículas a la que, para completar la serie, añaden una partícula más, la llamada gravitón, que se cree que transmite la interacción gravitatoria. Parece ser una consecuencia inevitable de las teorías de la gravedad y de la mecánica cuántica, y su espín tendrá que ser igual a dos. Nunca ha sido detectada y no esperamos verla en un futuro cercano.

                                                                                   Violación de la Simetría PC

La teoría no predice la masa de las partículas ni la intensidad de sus interacciones básicas, que tienen que ser determinadas experimentalmente. Esto se debe a que los parámetros básicos del modelo son constantes de la Naturaleza no relacionadas.

Si hacemos una lista completa de las constantes, nos encontramos con que hay veinte números que tienen que ser especificados en cualquier descripción matemática del modelo estándar. Muchos de ellos corresponden a las masas, otros describen aspectos de sus interacciones mutuas, tales como las tres constantes de acoplamiento gauge: Tenemos tres tipos de Campo de Yang-Mills gauge, cada uno con sus propias “constantes de interacción”, no los predice la teoría y todos tienen que ser medidos con gran precisión de manera experimental. Por otra parte, unos pocos parecen ser exactamente cero (tales como la “constante cosmológica de acoplamiento”, que describe la extensión a la cual el espacio vacío emite un campo gravitacional). Estos han sido, sin embargo, incluidos en la lista porque, por lo que sabemos, no hay nada en el modelo que las obligue a ser cero.

Independientemente del hecho irrefutable, de que el modelo estándar contiene veinte números de los que no sabemos porque toman los valores que tienen y, en consecuencia, no sepamos cómo obtenerlos a partir de primeros principios, lo cierto es que, el modelo para los físicos, ha resultado ser una herramienta extraordinaria que, a pesar de sus carencias, ha servido y sirve para el trabajo diario y resolver, muchos de los problemas que se plantean y surgen cuando se profundiza en ese mundo microscópico del que aún (y a pesar de lo que digan algunos), sabemos más bien poco que, bien mirado, y, si tenemos en cuenta que la única herramienta inicial para descubrirlo era nuestra Mente, en realidad, tampoco se puede decir que sea poco el avance conseguido desde Demócrito y Empédocles con sus átomos indivisibles y sus cuatro elementos.

                         Los cuatro elemetos de Empédocles

Todas las propiedades de las partículas fundamentales, los hadrones, núcleos atómicos, átomos, moléculas, sustancias, tejidos, plantas, animales, personas, planetas, sistemas solares, galaxias y quizá incluso el universo entero son consecuencia directa del modelo estándar. Y lo que es más, para la mayoría de las propiedades generales no tienen mucha importancia cual sea el valor exacto de esas constantes que aún no se conocen muy bien, tales como la masa de Higgs. Por ejemplo, el efecto de la interacción débil en las propiedades químicas de los átomos que es extremadamente difícil de detectar (debería dar una estructura helicoidal a los átomos de manera que puedan distinguir la derecha de la izquierda).

Claro que, alguna vez le oí a Tom Wood referirse a algunas de estas cuestiones, haciéndonos ver que, algunos, las mencionan como si sus significados sólo fueran cuestiones filosóficas enunciadas de cara al público, cuando, en realidad, en algunas ocasiones, tienen poca importancia práctica que se quiere enmascarar con aquella otra presentación subliminal o metafísica que, desde luego, caen lejos del campos estricto y muy serio (por cierto) de la Física.

       La dualidad onda-partícula, en el que se aprecia cómo un mismo fenómeno puede ser percibido de dos modos distintos, fue uno de los problemas filosóficos que planteó la mecánica cuántica. Tratándo sobre mecánica cuántica podríamos hablar de la filosofía de la física pero, nunca de la Física como filosofía.

Nosotros no somos capaces de deducir las propiedades de un escarabajo utilizando el modelo estándar y esto nunca va a cambiar. Imaginemos un examen de la siguiente cuestión:

Calcula el número de segmentos del Aselluz aquaticus a partir del modelo estándar. Se puede utilizar la lista adjunta para la masa de Higgs y los parámetros que violan la CP…

Nunca se podrá resolver tal tipo de problemas, ni es la intención de los Físicos Teóricos sugerir que ellos pueden hacer la labor de los Biólogos o la de los miembros de cualquier otra disciplina que no sea la Física. Lo que afirman es que las fuerzas de la Naturaleza responsables del número de segmentos de esas criaturas son conocidas, pero que el efecto es incalculable. A duras penas somos capaces de calcular los efectos de las fuerzas fundamentales en un simple hadrón tal como el protón (¡los resultados están a menudo desviados más de un cincuenta por ciento!), así que imagínese cuan imposible se hace la complejidad de un sistema formado por los 10²² átomos con la forma de un escarabajo.

Por primera vez, la ciencia logró fotografiar dos átomos vibrando juntos dentro de una molécula mediante un procedimiento en el cual se convirtió a un electrón en un “flash” para la mencionada foto. Ya de por sí el haber podido controlar el electrón para un fin específico abre perspectivas esperanzadoras con respecto a la posibilidad futura de poder controlar los productos químicos y sus reacciones a escala atómica.

Siguiendo las leyes de la mecánica cuántica, resulta que el cálculo de las propiedades de dos átomos juntos es muchísimo más complicado que el de un solo átomo y que las propiedades de la mayoría de los átomos son enormemente más difíciles de calcular que las del átomo más sencillo, el del hidrógeno.

Entender las fuerzas involucradas en nuestro Modelo Estándar es importante porque entonces también sabremos cuales son las leyes generales a las que obedecen estrictamente. Tenemos las leyes de conservación de la energía, de conservación del momento e incluso de conservación de la información; ésta última implica que los llamados fenómenos paranormales tendrán que ser explicados en términos de la física ordinaria, biología, psicología y así sucesivamente, pero si no se dan explicaciones realistas, estos temas no podrán ser de ninguna forma compatibles con todo lo que sabemos del modelo estándar, del que por cierto, nos que ¡tanto por saber!

No pocas veces la física nos puede parecer similar a uno de esos cuadros abstractos en los que, en un revoltujo incomprensible, aparecen figuras y colores que, la gente corriente no sabe como encajar y, tampoco alcanzar a poder ver la belleza allí presente, si, en realidad hay alguna.

Amargamente, y algo desalentado y hasta con una pizca de desesperación, oímos los lamentos de nuestro amigo Tom Woos que, comienza su largo comentario con:

“Introducir masa desde afuera; masa impropia como digo yo, no es nada nuevo y cada época lo ha hecho con los conocimientos físicos que poseía. Y lo desecho al entrar en contradicciones insalvables, con los nuevos conocimientos que vinieron. Primero para explicar la masa inercial de un cuerpo ordinario, los que tropezamos a diario, los que se usan para las demostraciones escolares. Después para explicar la masa y la interacción de los cuerpos del sistema solar. Posteriormente cuando ya no había discusión sobre la existencia del sistema solar y su mecánica de movimiento y se generalizaron los conocimientos físicos a todo el universo; tampoco en hombre se pudo explicar racionalmente, desde la física, físicamente, que era la masa, que es la inercia, que relaciona en lo profundo la masa y la gravedad.

El problema es el desespero, la enorme frustración científica que esto provoca en la sicología de un físico. Por eso tanta euforia, tanto fanatismo, por nada; es el deseo acumulado por anos. Por la normal aparición de un animal mas en el zoológico. Que los científicos dicen que es el traficante de masa y los periodistas informaron todo los que les vino en gana. Se vendieron como pan caliente, casi un complot científico-mediático.”

En mucho de lo que dice, lleva toda la razón…

emilio silvera

[?]

Ayer finalizábamos así la primera parte de este trabajo:

Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón seríaá hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.

De todas las maneras,  estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interracionan con él, es el efecto frenado el que les otorga la masa.

Claro que, esa, como otras conjeturas sobre los Océanos de Higgs y su dichosa Partícula “repartidora de masa”, no son más que conjeturas que, más adelante, debemos ir comprobando para poder escribirlas con letras de oro en el Libro de la Física, o, por el contrario, desecharlas como se ha hecho con tántas otras ideas y teorías frustradas que nunca llegaron a ninguna parte.

¡Los fotones de Yang-Mills adquieren su masa y el proncipio gauge se sigue cimpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente penso que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”. Si se admitía esto, ¿por qué no introducir más partículas y campos arbitrarios? Estas ideas se consideraron como simples modelos con los que jugart, sin mucho significado fundamental al que ahora se quiere llegar con el LHC pretendiendo hacer bueno todo aquello y, al menos los físicos, insisten en que, el campo y la partícula están ahí…¡ya veremos en qué queda todo esto! Son muchos los cabos sueltos y las cosas sin explicar.

En segundo lugar estaba lo que se llamó “teorema de Goldstone”. Ya se habían priducido antes modelos de partículas con “rotura espontánea de simetría”, pero para la mayoría de esos modelos, Jeoffrey Goldstone habia probado que siempre contenían partículas sin masa y sin espín. Muchos investigadores, por lo tanto, pensaron que la teoría de Higgs también debía contener esa partícula de Goldstone, sin masa y que esto era un inconveniente porque entre las partículas conocidas no había ninguna partícula de Goldstone. Incluso el propio Goldstone había advertido que el Modelo de Higgs no satisfaccía las condiciones para su demostración, así que no tenía que ser válido para este caso, pero todo el mundo estaba tan impresionado con las matemáticas del teorema que el Modelo de Huggs-Kibble no tuvo éxito durante mucho tiempo.

El bosón de Higgs pretende ser una parte integral de nuestra comprensión de la Naturaleza. Se trata de una partícula que es una excitación de lo que se llama el campo de Higgs. El campo de Higgs impregna todo el espacio y cuando algunas de las partículas fundamentales que viajan a través de este campo adquieren masa (al interaccionar con el Campo dónde, probablemente, ve frenada su marcha y su desplazamiento es más lento debido al medio por el que discurre su viaje). La cantidad de masa que adquieren depende de la fuerza en que interactúan con el campo de Higgs. Algunas particulas, como el electrón adquieren una pequeña masa, mientras que otras adquieren una masa mucho mayor.

Y así, el teorema de Goldstone se utilizó como un “teorema de imposibilidad”: si el espacio vacío no es simétrico, entonces no se puede evitar la presencia de partículas sin masa y sin espín. Ahora sabemos que, en nuestro caso, la letra pequeña invalida el teorema; las partículas de Goldstone se hacen incisibles debido a la invariancia gauge y no son más que las “partículas fantasmas” que encontró Feynman en sus cáculos. Además, debemos recordar que el Mecanismo Higgs no es una auténtica rotura de simetría.

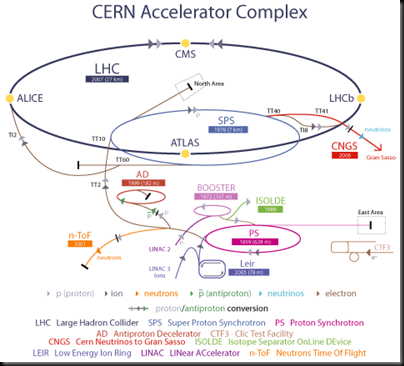
        Ingenios que quieren entrar en los campos de Higgs

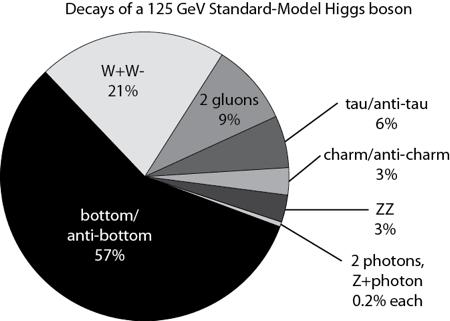
Un aspecto peculiar de esto es que este campo de Higgs que impregna en todo el espacio es parte de lo que llamamos espacio vacío o el vacío. Es sólo su impacto sobre las partículas que viajan a través de él y el bosón de Higgs que podemos observar en el laboratorio. El bosón de Higgs vive por un lapso muy corto de tiempo, así que no lo observan directamente, sino que más bien se observa que las partículas se descompone en y tienen que inferir su existencia a partir de eso. En la teoría actual que tenemos para comprender la naturaleza podemos hacer afirmaciones precisas acerca de qué fracción del tiempo que se desintegra en dos fotones en comparación con dos quarks abajo.

Claro que, algunos, me piden más profundidad en las explicaciones y, no se conforman con pasar por encima de las cuestiones, hay que entrar más en materia y dejar sentados algunos de los parámetros maemáticos que en todo esto están presente, y, para ellos…

Los físicos han buscado al bosón de Higgs por cerca de 50 años porque su descubrimiento completaría el Modelo Estándar de la física de partículas. El bosón de Higgs y su campo asociado explican cómo la simetría electrodébil se rompió justo después del Big Bang, lo que le dio a ciertas partículas elementales la propiedad de la masa. Sin embargo del Modelo Estándar no predice la masa de Higgs, y varios programas experimentales en el LEP del CERN, en el Tevatron de Fermilab y ahora el LHC del CERN habían intentado medir la masa de la partícula.

En el seminario llevado a cabo hoy en CERN como preludio a la mayor conferencia de física de partículas de este año, el ICHEP2012 en Melbourne, los experimentos ATLAS y CMS presentaron sus resultados preliminares en la búsqueda del Bosón de Higgs. Ambos experimentos observaron una nueva partícula en la región de masa entre 125-126 GeV.

“Observamos en nuestros datos claras señales de una nueva partícula, al nivel de 5 sigma, en la región de masa alrededor de 126 GeV. El impresionante rendimiento del LHC y ATLAS y el gran esfuerzo de mucha gente nos trajo a esta excitante etapa”, dijo la presentadora del experimento ATLAS Fabiola Gianotti, “pero se necesita más tiempo para preparar estos resultados para su publicación”

“Los resultados son preliminares pero la señal 5 sigma alrededor de 125 Gev que estamos viendo es dramática. Ésta es de hecho una nueva partícula. Sabemos que tiene que ser un bosón y es el bosón más pesado que hemos encontrado hasta ahora,” dijo el presentador del experimento CMS Joe Incandela. “Las implicaciones son muy significantes y es precisamente por esta razón que debemos ser extremadamente diligentes en todos nuestros estudios.”

¿Donde aparece el Higgs en todo esto?

Pues pasemos a hablar de teoría cuántica de campos, en ese tendremos unas densidades lagrangianas que dependerán del campo de cada partícula, dependiendo de su spin será un lagrangiano o otro, por ejemplo para N (a = 1,….N) campos escalares(omito fórmula).

.Al buscar el mínimo del potencial (en realidad un extremal de la acción, pero para lo que nos interesa a nosotros serán mínimos) resulta que hay varios posibles (con el mismo valor) pero para que la energía se minimice hace falta fijar un vacío (debido a que el Hamiltoniano depende del potencial y de unos términos positivos que van con las derivadas del campo). Ahora bien, inicialmente nuestra acción podría tener una simetría gauge global, es decir que al efectuar una transformación de un grupo sobre los campos la acción no cambia, al fijar el vacío la simetría se reduce a un subgrupo y algunos campos obtienen masa (originalmente ninguno tiene masa), pues bien el teorema de Goldstone lo que dice es que campos se quedan sin masa, estos son los bosones de Goldstone.

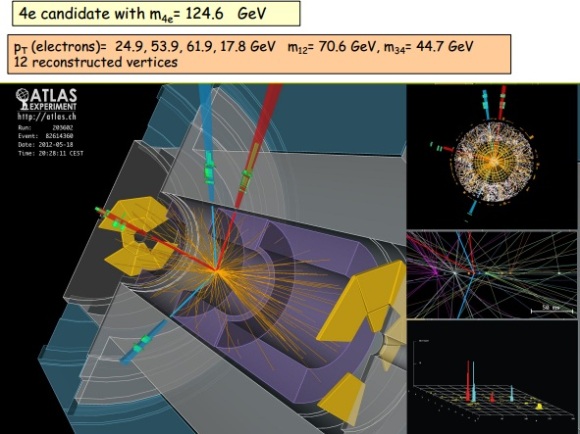
¿Y el higgs? ¬¬

Ya llegamos, en el apartado anterior hemos considerado transformaciones globales, pero por ejemplo en electromagnetismo tenemos transformaciones locales, así que hay que mirar lo que pasa en las transformaciones locales. Lo primero que pasa es que la derivada parcial no preserva los vectores (lo que hemos llamado antes ) igual que pasa en relatividad general, al hacer una transformación que depende de las coordenadas la derivada ya no es covariante, así que hay que buscar una covariante para seguir con lo que sabemos (en este caso la transformación se debe a un grupo gauge arbitrario, que no tiene porque ser el de difeomorfismos como en relatividad general. En este contexto aparecen los campos gauge que jugaran un papel similar al de la conexión en relatividad general y en el caso del electromagnetismo el campo gauge es el potencial electromagnético). Ahora al ser transformaciones locales, aparecen campos gauge que por similitud con el electromagnetismo escribiremos el lagrangiano de Yang-Mills igual que en el electromagnetismo F depende de los campos gauge, pero debido a que no es abeliano hay un termino extra que tiene que ver con las constantes de estructura del álgebra de Lie, . Ahora ya vien lo bueno, aparte del lagrangiano de la partícula también tenemos el de Yang-Mills, resulta que debido a la simetría local:

1. Los bosones de Goldstone desaparecen, es decir no son partículas físicas.
2. campos gauge obtienen masa

Pues eso es el efecto Higgs. Ahora para llegar ya al famoso bosón, en el modelo estandar no se pueden construir terminos de masa para las partículas debido a que no se pueden acoplar adecuadamente para ese propósito los campos de Yang-Mills y las partículas, debido a las simetrías que deben satisfacer (en general el famoso aunque cada campo tendrá una simetría concreta) y ahí es donde entra el bosón de Higgs, ya que el modelo más sencillo para añadir masa es justamente ese, añadir un doblete de campos escalares complejos y al romper la simetría …….. Higgs !!!!

Dos prestigiosos investigadores habñían sugerido de forma independiente que se podían construir modelos realistas dde partículas en los cuales, el sistema de Yang-Mills fuera responsable de la interacción débil y el mecanismo de Higgs-Kibble la causa de su corto alcance. Uno de ellos era el paquistaní Abdus Salam que estaba buscando modelos estéticos de partículas y pensó que la belleza de la idea de Yan-Mills era razón suficiente para intentar construir con ella un modelo de interacción débil. La partícula mediadora de la interacción débil tenía que ser un fotón de Yang-Mills y el mecanismo de Higgs-Kibble la única explicación aceptable para que esta partícula tuviera una cierta cantidad de masa en reposo.

Una simetría puede ser perfecta en el plano de las ecuaciones y resultar rota en el plano de las soluciones. Como decía Weinberg: «Aunque una teoría postule un alto grado de simetría, no es necesario que los estados de las partículas muestren la simetría. Nada me parece tan halagüeño en física como la idea de que una teoría puede tener un alto grado de simetría que se nos oculta en la vida ordinaria».

La teoría que unifica las interacciones electromagnéticas y débil se debe a Glashow, Salam y Weinberg que obtuvieron por ella el Premio Nobel de física de 1979. La dificultad esencial de esta teoría es que los bosones del estado inicial simétrico debían ser de masa nula (masa nula de los bosones de interacción origina una fuerza a gran distancia), mientras que se necesitan bosones intermedios (partículas que originan la fuerza) muy masivos para justificar la interacción débil (corto alcance) . El mecanismo de Higgs, permite resolver esa dificultad, mediante la ruptura espontánea de simetría hace masivos los bosones W y Z (interacción débil) y mantiene nula la masa del fotón (interacción electromagnética).

Los famosos diagramas de Feynaman, nos explican algunos mecanismos de los que se pueden producir (de hecho se producen) en ese misterioso campo de las partículas elementales cuando están presentes en cuertos lugares y se juntas con otros individuos de la especie.

Salam que estaba muy cerca de poder alcanzar la gloria…no llegaba a poder explicar y aplicar las reglas de Feynman y tuvo quer admitir que la teoría parecía estar llena de partículas fantasmas que estaban a punto de estropearlo todo. En estas, llegó el otro investigador, Steven Weinberg, que supo dar un paso más al formular con mucho más detalle un modelo sencillo en el cual indicaba con precisión los campos que existían y cómo podían interactuar. Pero se limitó a los leptones. Weinberg comprendió que, junto al fotón ordinario tenía que haber tres fotones de Yang-Mills pesados::

– Uno cargado positivamente.

– Otro cargado negativamente.

– Otro Neutro.

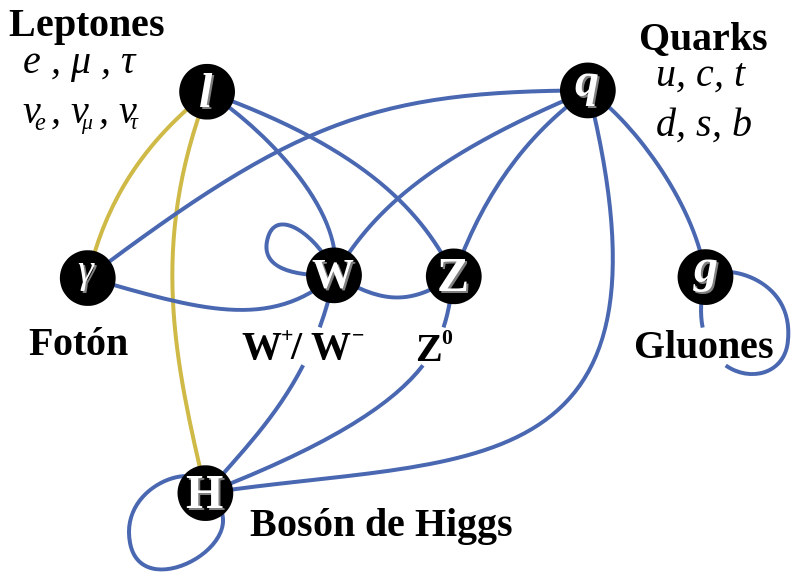
El panorama completo

En lo que se refiere a los fotones cargados, todo el mundo estaba de acuerdo en que estos se necesitarían para describir la interacción débil: serían los famoso bosones vectoriales intermediarios, W⁺ y W^–. De acuierdo con Weinberg, sus masas tenían que ser mayores de 60.000 MeV. Pero solos, estos bosones, vectoriales cargados eran suficientes para explicar todos los procesos de interacción débil que conocían en aquella época.  Que aparte de ellos y del fotón ordinario, y, también se necesita otro componente neutro (Weinberg le llamó Zº) no era evidente en absoluto. Se encontró que la masa del Zº tenía que ser un poco mayor que la de los bosones cargados.

De todo aquello surgió una tería para las interacciones débiles en las cuales jugaban un papel dominante distintos diagramas de Feynman, de los que se podían plasmar un número infinito para mostrar, de manera gráfica, los sucesos que acontecían en aquellos fenómenos de la radiación producida en la interacción débil. Pasado el tiempo y mirado con una mejor perspectiva, es fácil comprender todo aquello pero, en aquellos momentos en que se estaba gestando, las cosas no resultaban tan fáciles.

Después de todo aquello, se prestó más atención al mecanismo Higgs-Kibble y, algunos, como Veltman fueron muy escépticos con aquellas ideas, y, desde luego, no fue fácil converlo de que pudiéramos llamar vacío a algo lleno de partículas invisibles. ¿No delatarían dijo, su presencia por sus campos gravitatorios? La teoría puede ser formulada de tal manera que esos campos gravitatorios se compensen exactamente con otras partículas invibles o por una contribución misteriosa del propio espacio vacío.

Cómo consigue la Naturaleza enmascarar tan exacta y eficientemente esos factores de la gravedad que no podemos notar nada, es un misterio que continua siendo muy debatido hoy en día. Claro que, todo esto dejará de ser un misterio cuando un día (lejos aún en el futuro), podamos comprender la Gravedad Cuántica.

Miehntras todo esto sucede… ¡Dejémos volar nuestra imaginación! con ideas y teorías como la de los ¡Campos de Higgs! ¡Bosones que, generosos ellos, regalan masas a otras partículas! ¡Materia que no podemos ver pero que, dem manera acérrima, nos empeñamos en que sí está! ¡Fluctiaciones de vacío que rasgan el espacio-tiempo, y, que de vez en cuando, hace surgir nuevos universos! ¡Universos paralelos que nacieron sin vida! ¡Ciclos eternos en el que las cosas se repetin una y otra vez hasta el infinito! ¡Nuevos Big Bangs después del nuestro! ¡Agujeros negros en nuestro universo y, blancos al otro lado, en otro universo. Aquí recoge materia y, allú, la expulsa por el contrario, un Agujero Blanco! ¡Agujeros de Gusano que nos podrían llevar a otras galaxias! ¡El sueño de vencer (mejor burlar) a la velocidad de la luz, ese muro que nos tiene confinados en nuestro pequeño mundo, el Sistema Solar!

Después de leer todo esto, ¿por qué no dedicais aunque sólo sea una hora para pensar sobre ello?

emilio silvera

[?]

Lo único que no resulta ser lo mismo cuando se mira a través a través del microscopio (o, en la jerca de la física teórica, cuando se realiza una transformación de escala) es la masa de la partícula. Esto se debe a que el alcance de la fuerza parece mayor a través del microscopìo y, por lo tanto, la masa de la partícula parece ser menor. Nótese que esta situación es la opuesta a la que se presenta en vida corriente donde un grano de arena parece mayor -¿más pesado, por lo tanto?- cuando se observa con un microscopio.

                                             Granos de arena vistos al microscopio

Una consecuencia de todo esto es que en una teoría de Yang-Mills el termino de masa parece desaparecer cuando se realiza una transformación de escala, lo que implica que a través del microscopio se recupera la invariancia gauge. Esto es lo que causa la dificultad con la que se enfrentó Veltman. ¿Se puede observar directamente el potencial vector de Yang-Mills? Parece que puede observa4rse en el mundo de las cosas grandes, pero no en el mundo de lo pequeño. Esto es una contradicción y es una raz´`on por la que ese esquema nunca ha podido funcionar adecuadamente.

En 2009, la empresa canadiense D-Wave Systems, conjuntamente con la NASA, desarrolló un ordenador cuántico de 128 cubits. Rainer contiene 128 dispositivos físicos (pequeños aros de metal niobidio) que a muy baja temperatura actúan como sistemas cuánticos con dos niveles (es decir, cubits) como consecuencia de la superconductividad.

¡Había una salida! Pero ésta procede de una rama muy diferente de la física teórica, la física de los metales a muy bajas temperaturas. A esas temperaturas, los “fenómenos cuánticos” dan lugar a efectos muy sorprendentes, que se describen con teorías cuánticas de campos, exactamente iguales a las que se utilizan en la física de partículas elementales. La física de partículas elementales no tienen nada que ver con la física de bajas temperaturas, pero las matemáticas son muy parecidas.

En algunos materiales, el “campo” que se hace importante a temperaturas muy bajas podría ser el que describe cómo los átomos oscilan alrededor de sus posiciones de equilibrio, o el que describe a los electrones en este tipo de material. A temperaturas muy baja nos encontramos con los “cuantos” de esos campos. Por ejemplo, el “fonón” es el cuanto del sonido. Su comportamiento recuerda al fotón, el cuanto de la luz, salvo que los números son muy diferentes: los fonones se propagan con la velocidad del sonido, a cientos o quizá miles de metros por segundo, y los fotones lo hacen a la velocidad de la luz que es de 300.000 km/s, ¡aproximadamente un millón de veces más deprisa! Las partículas elementales en las que estamos interesados generalmente tienen velocidades cercanas a las de la luz.

El fonon es la partícula elemental del sonido, como el foton lo es en la luz..

Uno de los “fenómenos cuánticos” más espectaculares que tienen lugar en los materiales muy fríos es la llamada superconductividad, fenómeno consistente en el hecho de que la resistencia que presenta ese material al paso de la corriente eléctrica se hace cero. Una de las consecuencias de ese estado es que el material no admite la más mínima diferencia de potencial eléctrico, porque ésta sería inmediatamente neutralizada por una corriente eléctrica “ideal”. El material tampoco admite la presencia de campos magnéticos porque, de acuerdo con las ecuaciones de Maxwell, la creación del campo magnético está asociada con una corriente eléctrica inducida, que al no encontrar resistencia neutralizaría completamente el campo magnético. Por lo tanto, en el interior de un superconductor no se puede crear ni un campo electrónico ni magnético. Esta situación sólo cambia si las corrientes inducidas son muy elevadas, como ocurre cuando se somete el superconductor a los campos de imanes muy potentes y que perturban el material. No siendo capaz de resistir una fuerza tan brutal, pierde la superconductividad y se rinde permitiendo la existencia de un campo magnético en su interior.

¿Pero, qué tiene que ver un superconductor con las partículas elementales? Bien, un material superconductor se puede entender como un sistema en el cual el campo electromagnético es un campo de muy corto alcance. Está siendo apantallado y, sin embargo, es un campo de Maxwell, un campo gauge. ¡Esto es lo que hace interesante un superconductor para alguien que quiera describir la interacción débil entre partículas como una teoría gauge! ¡Qué característica tan bella de la física teórica! Se pueden comparar dos mundos completamente diferentes simplemente porque obedecen a las mismas ecuaciones matemáticas.

¿Cómo funciona un superconductor? La verdadera causa de este fenómeno peculiar la descubrieron John Bardeen, Leon N. Cooper y John R. Schrieffer por lo que recibieron el premio Nobel en 1972). Los electrones de un trozo sólido de material tienen que reunir al mismo tiempo dos condiciones especiales para dar lugar a la superconductividad: la primera es apareamiento y la segunda condensación de Bose.

“Apareamiento” significa que los electrones forman pares y actúan en pares, y los que producen la fuerza que mantiene los pares unidos son los fonones. En cada par, los electrones rotan alrededor de su propio eje, pero en direcciones opuestas, de manera que el par (llamado “par de Cooper”), en su conjunto, se comporta como si no tuviera rotación (“momento angular”). Así, un par de Cooper se comporta como una “partícula” con espín 0 y carga eléctrica -2.

La “condensación de Bose” es un fenómeno típicamente mecánico-cuántico. Sólo se aplica a partículas con espín entero (bosones). Al igual que los lemmings, los bosones se agrupan juntos en el estado de menor energía posible, Recuérdese que a los bosones les gusta hacer a todos la misma cosa. En este estado todavía se puede mover, pero no pueden perder más energía y, en consecuencia, no sufren ninguna resistencia a su movimiento. Los pares de Cooper se mueven libremente, de manera que pueden crear corrientes eléctricas que no encuentran ninguna resistencia. Un fenómeno parecido tiene lugar en el helio líquido a muy bajas temperaturas. Aquí los átomos de helio forman una condensación de Bose y el líquido que forman puede fluir a través de los agujeros más pequeños sin la más mínima resistencia.

                                  Condensado de Bose

Como los electrones por separado tienen espín ⅟₂ no pueden sufrir una condensación de Bose. Las partículas cuyo espín es igual a un entero más un medio (fermiones) tienen que estar en estados cuánticos diferentes debido al principio de exclusión de Pauli. Esta es la razón por la que la superconductividad sólo se puede producir cuando se forman pares. Sí, comprendo que estas afirmaciones le sugerirán varias preguntas y me disculpo por adelantado, pero de nuevo he traducido fórmulas a palabras, lo que implica que el razonamiento pueda parecer poco satisfactorio. ¡Simplemente tome esto como una cierta “lógica cuántica” difícil de manejar! Fueron el belga François Englert, el americano Robert Brout y el inglés Peter Higgs los que descubrieron que la superconductividad podría ser importante para las partículas elementales. Propusieron un modelo de partículas elementales en el cual partículas eléctricamente cargadas, sin espín, sufrían una condensación de Bose. Esta vez, sin embargo, la condensación no tenía lugar en el interior de la materia sino el vacío. Las fuerzas entre las partículas tenían que ser elegidas de tal manera que se ahorrara más energía llenando el vacío de estas partículas que dejándolo vacío. Estas partículas no son directamente observables, pero podríamos sentir el estado, en cuyo espacio y tiempo están moviéndose las partículas de Higgs (como se las conoce ahora) con la mínima energía posible, como si el espacio tiempo estuviera completamente vacío.

Haber encontrado el bosón de Higgs puede resolver el misterio de la composición de masa de todos los objetos. Esta masa está presente en las partículas subatómicas y sin ellas la materia sólida no podría existir. El bosón de Higgs está relacionado a un campo energético, que se llama el campo de Higgs, el mismo que está presente en todo el universo de igual forma como el agua inunda una piscina. Es formando parte de ese campo, que las diversas partículas, como los protones, neutrones, electrones y otras, adquieren su masa. Las partículas más pequeñas encuentran menos dificultades para desplazarse, y las más grandes lo hacen con mayor dificultad. De todas las maneras, quedan muchas por explicar. Fandila nos prguntaba que, ¿de dónde adquiere su masa el mismo Bosón de Higgs?

Las partículas de Higgs son los cuantos del “campo de Higgs”. Una característica de este campo es que su energía es mínima cuando el campo tiene una cierta intensidad, y no cuando es nulo. Lo que observamos como espacio vacío no es más que la configuración de campo con la menor energía posible. Si pasamos de la jerga de campos a la de partículas, esto significa que el espacio vacío está realmente lleno de partículas de Higgs que han sufrido una condensación Bose”.

Este espacio vacío tiene muchas propiedades en común con el interior de un superconductor. El campo electromagnético aquí también es de corto alcance. Esto está directamente relacionado con el hecho de que, en tal mundo, el fotón tiene una cierta masa en reposo.

Y aún tenemos una simetría gauge completa, es decir, la invariancia gauge no se viola en ningún sitio. Y así, sabemos cómo transformar un fotón en una partícula “con masa” sin violar la invariancia gauge. Todo lo que tenemos que hacer es añadir estas partículas de Higgs a nuestras ecuaciones.

La razón por la que el efecto de invariancia gauge en las propiedades del fotón es tan diferente ahora es que las ecuaciones están completamente alteradas por la presencia del campo de Higgs en nuestro estado vacío. A veces se dice que “el estado vacío rompe la simetría espontáneamente”. Esto no es realmente correcto, pero el fenómeno está muy relacionado con otras situaciones en las que se produce espontáneamente una rotura de simetría.

Higgs sólo consideró campos electromagnéticos “ordinarios”, pero, desde luego, sabemos que el fotón ordinario en un vacío auténtico no tiene masa en reposo. Fue Thomas Kibble el que propuso hacer una teoría de Yang-Mills superconductora de esta forma, simplemente añadiendo partículas sin espín, con carga de Yang-Mills en vez de carga ordinaria, y suponer que estas partículas podían experimentar una condensación de Bose. Entonces el alcance de las interacciones de Yang-Mills se reduce y los fotones de Yang-Mills se convierten en partículas con espín igual a 1 y masa distinta de cero.

La discontinuidad manifiesta junto con la invariancia de escala (autosemejanza), que presenta la energía de las fluctuaciones del vacío cuántico. Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un campo que lo inunda todo llamado campo de punto cero.

Algunos físicos proponen una controvertida teoría en la que un extraño tipo de materia, el Singlet de Higgs, se movería hacia el pasado o el futuro en el LHC. ¡Qué imaginación! Claro que, puestos a imaginar…

Bien sabido es que mientras más profundizamos en el conocimiento de los secretos del mundo que nos rodea, más interrogantes y misterios sin resolver se nos muestran. Cada vez que abrimos una puerta, llegamos a una habitación que tiene otras muchas por abrir. Es la búsqueda incesante del hombre, su insoslayable afán por saber el por qué, el cómo y el cuándo de todas las cosas.

¿Estaremos entrando en una especie de locura?

Bueno…

Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón seríaá hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.

De todas las maneras,  estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interracionan con él, es el efecto frenado el que les otorga la masa.

emilio silvera

[?]