Sir Isaac Newton [1642-1727]

La grandeza de Newton ha sido reconocida por todos (polémicas aparte), y, el mismo Einstein -de alguna manera el que finalizó su teoría de la gravitacíon universal- así lo dejó plasmado en las palabras siguientes:

Observad las estrellas y aprended de ellas,

En honor al maestro todas deben girar,

Cada una en su trayectoria, sin un ruido,

Siguiendo el principio de Newton.

Mewton elaboró una explicación cuantificada matemáticamente de la gravitación que abarcaba por igual fenómenos terrestres y celestes. Al hacerlo demolió la división aristotélica del universo en dos ámbitos, uno por encima y otro por debajo de la Luna, y creó una base física para el Universo copernicano.

Mewton elaboró una explicación cuantificada matemáticamente de la gravitación que abarcaba por igual fenómenos terrestres y celestes. Al hacerlo demolió la división aristotélica del universo en dos ámbitos, uno por encima y otro por debajo de la Luna, y creó una base física para el Universo copernicano.

La perfección y seguridad con la que realizó esta tarea fueron tales que su teoría llegó a ser considerada durante más de dos siglos, como algo cercano a un mensaje de Dios. Aún hoy, cuando la dinámica newtoniana es contemplada como sólo una parte de la tela más vasta pintada por la relatividad de Einstein, la mayoría de nosotros seguimos pensando en términos newtonianos, y las leyes de Newton son eficaces para guiar las naves espaciales a la Luna y los planetas.

de donde:

F es el módulo de la fuerza ejercida entre ambos cuerpos, y su dirección se encuentra en el eje que une ambos cuerpos.

G es la constante de Gravitación Universial.

Sin embargo, el hombre cuya explicación del Cosmos vive en la mente de más de mil millones de personas era uno de los más extraños y difícilmente accesibles individuos que haya vivido nunca y, en su vida privada tenía aficiones insospechadas como la de aquellos papeles de Alquimía comprados en una Subasta y que estaban dentro de un viejo Baúl de Newton.

Una muestra de los Papeles de Newton conservados en la Bibliteca de Israel

Claro que Newton era mucho más que esos escarceos esporádicos que pudiera hacer por la Alquimia. Cuando la Universidad se vio oblugada a cerrar sus puertas obligada por la Peste de 1665, envió a todos sus estudiantes a casa. Mewton regresó a la Granja de su padre y, tenía por aquel entonces 22 años. En su pueblo natal de Woolsthorpe disfrutó de dos años de vaciones forzosas que le fueron muy frrctíferas y más para la Historia de la Ciencia.t

Allí, alejado de todos y en plena Naturaleza, llevando una vida bucólica y relajada. Newton pudo estar en contacto directo con la Naturaleza que amaba y se pasaba el día pensando sobre las cuestiones que llamaban su atención. Idealesgeneiales sobre la naturaleza de la luz y sus experimentos del prisma, una mezcla de colores del espectro que, en realidad, abrió el camino a una óptica más avanzada.

La naturaleza de la luz

Apuntes sobre la Naturaleza de la luz

Sus estudios sobre la naturaleza de la Lus y los telecopios son ahora bien conocidos por todos y también los avances a que dieron lugar todas a quellas ideas de un chico de 22 años. De aquellos etudios salieron trabajos de gran importancia que le dieron al mundo buenas herramientas para avanzar en otros campo de la Física.

El siglo XVIII, ha sido llamado Siglo de las Luces, porque albergó un movimiento de verdadera revolución intelectual, terreno abonado por matemáticos y científicos como el italiano Galileo, el polaco Copérnico, el francés Descartes, el holandés Huygens y, los británicos Charles Darwin e Isaac Newton.

El año en que moría Galileo, nació Isaac Newton en Woolsthorpe, una humilde aldea inglesa, y en el seno de una familia sumamente modesta, esencialmente campesina, que no contaba con grandes medios de fortuna. Su padre, labriego analfabeto,  murió meses antes de que naciera el futuro sabio. El muchacho crecía y se desarrollaba en un ambiente rural en el que no se le ofrecían grandes problemas intelectuales; pese a que su gran curiosidad y su notable inteligencia, que empezaron a manifestarse en los primeros juguetes que construyó para él y para sus amigos: pequeños molinos de viento, papalotes, relojes hidráulicos y otros ingeniosos artefactos. Pronto dedicó casi todo su tiempo al estudio apasionado de las matemáticas, devorando en escasos meses todos los libros que contenían las pequeñas bibliotecas locales.

A los catorce años dejó de asistir a la escuela para ayudar a su madre, viuda por segunda vez, por lo que regresó a la explotación de la granja familiar. Abandonar sus estudios hizo que el joven Newton se sintiera profundamente desgraciado. Sus labores campesinas, no le dejaban tiempo para sus especulaciones y lecturas, o para la construcción de sus artefactos, pero un tío suyo, William Ayscough, que se dio cuenta de cuan penosa era para el joven aquella situación, y, como era hombre ilustrado, miembro del Trinity College de Cambridge, aconsejó a la madre para que el joven Newton volviera a la escuela, esta vez con la intención de prepararlo para su ingreso en la Universidad de Cambridge, cosa que tuvo lugar en 1661.

A partir de aquel día, el progreso de Newton fue rapidísimo. Cuatro años más tarde recibía su diploma de bachiller, y en el transcurso de aquel tiempo consiguió impresionar muy profundamente, con sus vastos conocimientos y su extraordinaria rapidez mental, a sus condiscípulos y maestros. El mismo año en que recibió su diploma descubrió el famoso teorema en el que desarrollaba el binomio que todos los estudiantes de álgebra conocen hoy en día con el nombre de su descubridor: el binomio de Newton. Y unos meses después descubrió los elementos del cálculo diferencial o integral, a los que dio el nombre de “fluxiones”. Era una etapa singularmente creadora, porque, como es bien sabido, los grandes matemáticos -en esto se parecen a los atletas- dan lo mejor de sus esfuerzos durante los años juveniles; el matemático que a los treinta años no ha producido ningún descubrimiento valioso puede considerarse hombre fracasado.

Newton escribió,- a los 24 años, mayo de 1666-: “Conseguí adivinar los principios del cálculo integral y el método para calcular el área de las curvas y el volumen de los sólidos, y aquel mismo año empecé a pensar en cómo calcular la gravedad con relación a la órbita de la Luna, y habiendo comparado la fuerza requerida para mantener a la Luna en su órbita con la fuerza de la gravedad en la superficie de la Tierra, me pareció que coincidían bastante exactamente. Todo esto ocurría en 1665 y 1666, pues en aquellos años me hallaba yo en la plenitud de mis fuerzas.”

En aquel mismo período empezó a trabajar también en una serie de experimentos acerca de la luz y los colores: el resultado de sus investigaciones fue presentado en un estudio que entregó a la Royal Society de Londres años más tarde, en 1672 ,el año en que fue elegido miembro de aquella sociedad de sabios.

En 1684 tres miembros de la Royal Society, el astrónomo Edmund Halley, Christopher Wren, arquitecto de la catedral de de Londres, y el físico Robert Hooke, mantenían en Londres una animada discusión que acabó en una apuesta: ¿qué tipo de trayectoria describen los planetas alrededor del Sol? Wren ofreció 40 chelines a quien aportara la solución.

De los tres, Halley fue el que más se empeñó en encontrar una solución, hasta el punto de viajar a Cambridge para trasladar la pregunta a Newton, el excéntrico profesor de matemáticas. Allí pudo preguntarle directamente: ¿qué tipo de trayectoria describen los planetas alrededor del Sol? Sobre esta entrevista no sabríamos nada si no llega a ser por Abraham de Moivre, gran matemático y amigo de Newton, que dejó escrito lo siguiente sobre este encuentro:

Newton contestó inmediatamente que era una elipse. El doctor, lleno de alegría y asombro, preguntó cómo lo sabia. “Porque lo he calculado”, contestó. Entonces el doctor le pidió que le mostrase los cálculos. Newton buceó en su baúl, entre sus papeles, pero no lo encontró. Prometiéndole que los volvería a reproducir.

Telescopio de NewtonSus

Halley y Newton

Ese baúl lo heredó su encantadora sobrina Catherine Conduitt y a través de la descendencia, el baúl terminó en manos del vizconde de Lymington. Casi nadie había visto nunca los documentos que contenía el baúl, y una leyenda cuenta que una vez un obispo, picado por la curiosidad, examinó el contenido del baúl y lo cerró inmediatamente horrorizado. Durante mucho tiempo el contenido del baúl siguió siendo un misterio y su contenido calificado como no apto para la difusión.

El vizconde de Lymington, acuciado por algunos problemas financieros, un divorcio y algunos problemas de impuestos, decide poner a la venta el conjunto de documentos de Newton que su familia poseía desde hacía más de doscientos años.

En 1936, se subasta en Sotheby’s (Londres) el contenido de un baúl metálico lleno de manuscritos de Isaac Newton. Casi todo el lote fue adquirido por John Maynard Keynes, el famoso economista, al que gustaba coleccionar textos científicos antiguos. (el resto de la historia ya os la conté arriba).

Fotografía de la casa natal de Isaac Newton  en la localidad de Woolsthorpe , en Lincolnshire, donde nació prematuramente aquel 4 de enero de 1643 (aunque en algunas referencias se menciona que esta es la casa donde vivió en Grantham años después)  . Newton era hijo único, el hijo póstuno de un pequeño terrateniente analfabeto. Era tan pequeño al nacer que su madre ,  Hannah Ayscough, diría que cabía en una botella de cuarto. Su padre había muerto unos meses antes y con sólo tres años tuvo que abandonar la casa materna cuando Hannah se casó por segunda vez y su nuevo marido no quiso hacerse cargo del niño.Durante el resto de su infancia viviría en casa de su abuela materna , a dos kilómetros de distancia de su madre , algo que seguramente influiría en el carácter silencioso, reservado y poco sociable de Newton a lo largo de su vida. De todas formas es difícil juzgar la personalidad de una mente tan poderosa como la del gran matemático inglés , porque su forma de ver el mundo no puede ser igual a la que tenemos los demás, muy por debajo de su capacidad intelectual.

Newton, que había nacido en el mismo año de la muerte de Galileo Galilei, sustituyó el telescopio refractor de Galileo , que tenía una gran lente en la parte delantera para recoger la luz pero que Newton, por su experiencia con la refracción de la luz, sabía que distorsionaba los colores. Así desarrolló el telescopio reflector que empleaba un espejo en lugar de una lente para recoger la luz lo que lo hacía más barato y más eficiente. La Royal Society le pediría que construyese un segundo telescopio y viendo que funcionaba a la perfección le admitieron inmediatamente en la sociedad científica. Sin embargo, Newton no estaría contento con la fama que había ganado con este invento, ya que recibía muchas cartas. Escribiría al secretario de la Royal Society quejándose porque había “sacrificado mi tranquilidad, una cuestión de verdadera importancia” Así era Newton, siempre huyendo de la fama para que no interrumpieran su trabajo, aunque no estaba exento de ambición.

Durante un tiempo se inspiró en los libros de René Descartes, un espíritu afín al suyo. Ambos tenían mucho en común: criados por sus abuelas, niños frágiles y solitarios y con una vida interior muy fuerte que modeló sus caractéres. descartes le hablaba de lo que era el conocimiento humano y, muchos de aquellos pensamientos pervivieron en su intelecto.

La teoría cartesiana del torbellino del sistema solar se convirtió en el estímulo para la demostración de Newton de que los torbellinos no podían explicar las leyes de Kepler del movimiento planetario. La importancia que asignó Descartes a la descripcion algebraica del movimiento alentó a Newton a elaborar una dinámica escrita en una fórmula alternativa del algebra, la geometría. Como esto aún no era matemáticamente factible, Newton halló necesario inventar una nueva rama de la matemática, el cálculo infinitesimal. Éste puso la geometría en movimiento . Las parábolas e hipérbolas que Newton trazó en el papel podían ser analizadas como resultado de un punto en movimiento como la punta del palillo con el que Arquímedes trazaba figuras en la arena. En palabras de Newton: “Se describen líneas, y por ende se generan, no por la oposición de partes, sino por el movimiento continuo de puntos.”

En 1684, Halley visitó a Newton y le formuló su pregunta, y cual sería su asombro cuando éste le respondió inmediatamente: serán elipses. ¿Cómo Newton lo sabía? Fácil, lo había calculado hacía ya un tiempo, en sus anni mirabiles -20 meses entre 1665 y 1666 tiempo que paso confinado en su casa natal a causa de una epidemia de peste que azotó Cambridge-. Diez años después, en 1676, terminó su estudio que por supuesto no publicó. Así, a petición de Halley, Newton revisó y completó sus cálculos y se los envió a Halley. La insistencia de Halley y el genio de Newton convirtió ese pequeño manuscrito en la la obra científica más importante jamás escrita: Philosophiae naturalis principia mathematica. La publicación de los Principia de Newton donde Newton mostraba la equivalencia de su ley de gravitación universal, la atracción gravitatoria es lo que mueve a los planetas, con las leyes del movimiento planetario de Kepler dio término a la Revolución Copernicana y las predicciones que permitía su modelo matemático del universo inauguraban una nueva era para la ciencia. Con un ejemplar de la primera edición de los Principia  editado en Londres en 1687 y costeado de los bolsillos del propio Halley -por suerte para éste se vendió muy bien y ya 4 años después era casi imposible encontrar en ejemplar- terminamos esta sección.

Los logros científicos de Isaac Newton son de sobra conocidos. Sin embargo, tuvio otras fasetas menos conocida del precursor de la ciencia moderna: su cargo como intendente de la Real Casa de la Moneda en Londres, por ejemplo. Es posible que Newton pueda ser, sino el que más, uno de los científicos más grandes de la historia de la Humanidad, y, como siempre se exagera, se él se llegó a decir:

“La naturaleza y sus leyes yacían ocultas en la noche.
Dijo Dios: “¡Sea Newton!”, y se hizo la luz.”

Sus estudios sobre problemas de óptica resultaron también de inmensa importancia científica. Fue Newton el primero en demostrar, con ayuda de un prisma, que la luz del sol, que en apariencia es blanca, se compone en realidad de una serie de colores tales como los que forman el arco iris. Los rayos de estos colores dan al mezclarse la impresión de blancura; pero cada haz de color resulta claramente separado de los demás al pasar por un prisma por la razón de que su índice de refracción -es decir, el espacio en que se desvía de la línea recta al pasar por un cuerpo de densidad superior al aire, tal como un prisma de cristal- es ligeramente diferente de los demás. Así se explica, entre otros, el fenómeno del arco iris, en que las gotas de agua difusas en la atmósfera lluviosa obran a manera de pequeños prismas y provocan la refracción de cada color y el fenómeno de las bandas de color en el cielo después de la lluvia.

Estas demostraciones de Newton no habían sido motivadas por un interés puramente teórico por los fenómenos de la luz y la óptica, sino que eran el resultado parcial de sus esfuerzos encaminados a construir un telescopio más eficaz que los de su tiempo. Newton se interesaba por todo; por la luz, por los problemas de propagación de las olas o la aplicación del infinito a las matemáticas, a la astronomía e, incluso, a la teología.

Pero, como es bien sabido, la parte de su obra que mayor fama le ha dado es su descubrimiento de la ley universal de gravitación. Acerca de este descubrimiento, Voltaire ayudó a divulgar una pequeña leyenda: Newton, dormía bajo un manzano y fue despertado, bruscamente, por la caída de una manzana. Este hecho lo condujo a una prolongada reflexión que lo llevó a resolver, científicamente, el problema de la gravitación universal. Curiosamente, ése árbol murió en 1820 y sus astillas se convirtieron en reliquias, y algunas pueden verse en la Royal Society, en una colección dedicada a Newton.

Las epidemias de peste, varias veces interrumpieron sus enseñanzas en la Universidad y el Trinity College y solo en 1686 empezó a redactar en latín su obra fundamental Philosophia Natarals Principia Mathematica, obra que escribió en pocos meses. En 1695, tras una breve incursión en política, el canciller Montaigne, lo nombró como encargado de la Casa de Acuñación de Moneda, de la que fue Director General, lo que significó un situación económica estable y, como alto funcionario le permitió realizar numerosas actividades sociales. En 1703 fue nombrado presidente de la Royal Society; dos años después, la reina Ana le concedió el título de caballero, es decir, desde entonces, debió citársele como sir Isaac Newton.

La complejidad de los problemas que se planteaba Newton era tal que sufrió crisis de nervios, y hay que dejar constancia que, muchas veces, pospusiera la publicación de sus resultados. Por ejemplo, el principio de gravitación lo descubrió en 1666; sin embargo, tardó unos veinte años en publicar su Principia Mathematica. Podemos imaginar cuán desesperadamente complejo era el problema que se había planteado. No había ningún instrumento matemático capaz de enfrentarse con aquel problema, y para hallar la solución, tuvo que inventar un nuevo instrumento matemático, el cálculo integral. Gracias a él pudo satisfacer su conciencia científica y dar a conocer la ley de gravitación en el tercer volumen de su gran libro. Principia.

Newton vivió hasta edad muy avanzada. El mal de piedra y la pulmonía le hicieron sufrir durante los últimos años. Murió en 1727 y fue enterrado en compañía de los más ilustres ingleses, en la abadía de Westminster.
En su epitafio puede leerse : “Honró al género humano.”

recopilado por emilio silvera

[?]

Muchos han sido los que han querido explicar lo que es la consciencia.  En 1.940, el gran neurofisiólogo Charles Sherrington lo intentó y puso un ejemplo de lo que él pensaba sobre el problema de la consciencia. Unos pocos años más tarde también lo intentaron otros, y antes, el mismo Bertrand Russell hizo lo propio, y en todos los casos, con más o menos acierto, el resultado no fue satisfactorio por una sencilla razón: nadie sabe a ciencia cierta lo que en verdad es la consciencia y cuales son sus verdaderos mecanismos; de hecho, Russell expresó su escepticismo sobre la capacidad de los filósofos para alcanzar una respuesta:

“Suponemos que un proceso físico da comienzo en un objeto visible, viaja hasta el ojo donde se convierte en otro proceso físico en el nervio óptico y, finalmente, produce algún efecto en el cerebro al mismo tiempo que vemos el objeto donde se inició el proceso; pero este proceso de ver es algo “mental”, de naturaleza totalmente distinta a la de los procesos físicos que lo preceden y acompañan. Esta concepción es tan extraña que los metafísicos han inventado toda suerte de teorías con el fin de sustituirla con algo menos increíble”.

La conciencia, de alguna manera, está conectada con el universo

Está claro que en lo más profundo de esta consciencia que no conocemos, se encuentran todas las respuestas planteadas o requeridas mediante preguntas que nadie ha contestado. Para poder llegar a esos conocimientos tan profundamente escondidos dentro de nosotros, debemos observar la Naturaleza que, habiendo logrado traernos hasta aquí, a partir de la materia “inerte”, es la que, contiene todos y cada uno de los datos que nos dirán lo que somos, de dónde venimos y hacia dónde vamos.

En variadas oportunidades he mencionaba el cosmos y la gravedad junto con la consciencia y, en realidad, con más o menos acierto, lo que estaba tratando era hacer ver que todo ello es la misma cosa: universo-galaxia-mente. Nada es independiente en un sentido global, sino que son partes de un todo y están estrechamente relacionados.

Una galaxia es simplemente una parte pequeña del universo, nuestro planeta es una mínima fracción infinitesimal de esa galaxia, y nosotros mismos podríamos ser comparados (en relación a la inmensidad del cosmos) con una colonia de bacterias pensantes e inteligentes. Sin embargo, todo forma parte de lo mismo, y aunque pueda dar la sensación engañosa de una cierta autonomía, en realidad todo está interconectado y el funcionamiento de una cosa incide directamente en las otras.

[?]

MATEMÁTICAS | En Alemania

Un joven de 16 años resuelve un enigma matemático planteado por Newton hace 350 años

ELMUNDO.es | Madrid

           Shouryya Ray. | E.M.

Un adolescente de 16 años ha logrado resolver un enigma matemático planteado por Isaac Newton hace más de 350 años. Shouryya Ray, el joven prodigio que ha sorprendido a la comunidad científica, es un alumno de origen indio que estudia en una escuela secundaria de Dresden, en Alemania.

Este ‘cerebrito’ ha logrado resolver dos teorías de dinámicas de partículas que hasta ahora los físicos sólo podían calcular de manera aproximada con potentes ordenadores.

Gracias a sus ecuaciones, ahora se podrá calcular con exactitud la trayectoria de un proyectil afectado por la gravedad y por la resistencia del aire (el problema propuesto por Newton hace más de tres siglos), y también predecir cómo golperará y rebotará en una pared.

Ray emigró a Dresden desde Calcutta hace cuatro años sin hablar ni una palabra de alemán, un idioma que ahora domina. Sus profesores se dieron cuenta en poco tiempo de que poseía una inteligencia extrordinaria, y le permitieron saltarse dos cursos para que se encontrara en el nivel adecuado para sus capacidades.

Su habilidad para las matemáticas también se debe sin duda a que desde que era muy pequeño, su padre, un ingeniero, le desafiaba con problemas aritméticos. De hecho, antes de cumplir 10 años ya era capaz de resolver ecuaciones complejas.

El joven descubrió los problemas planteados por Newton durante una visita escolar a la Universidad de Dresden, en la que los profesores le explicaron que eran enigmas “irresolubles”. Ahí le ofrecieron datos experimentales con los que analizar la trayectoria del lanzamiento de una pelota. Los métodos para resolverlo eran aproximaciones y Ray decidió -«por curiosidad e ingenuidad de estudiante», explicó a ‘The Sunday Times’- buscar la solución definitiva.

“Me pregunté a mí mismo: ¿por qué no intentarlo?“, recuerda el joven. “No me podía creer que no existiera una solución”.

Ray afirma que disfruta mucho de la “belleza intrínseca” de las matemáticas, pero asegura con humildad que no es “ningún genio”, y confiesa que le gustaría también destacar en otras actividades, además de las matemáticas. “Me encantaría jugar mejor al fútbol”, ha reconocido al diario británico ‘The Daily Mail’.

Leído en El Mundo.es

[?]

Si no fueron los mejores matemáticos astronómicos, los chinos fueron al menos los mejores cartógrafos de estrellas que existieron antes del Renacimiento. Su primer mapa estelar se remonta al menos a 2000 a. C. y se trata de un relieve esculpido en la roca de un barranco en Jiangjunya, en la provincia de Jiangsu. Este relieve contiene numerosas estrellas, así como cabezas humanas y de animales. Hay discos que representan el Sol en posiciones estacionales, donde la Luna y un cierto número de estrellas aparecen a lo largo de las estaciones. Por su posición y su apariencia se puede reconocer que esta zona brillante de la esfera celeste es la Vía Láctea; en el relieve están representados los espacios vacíos y las divisiones que aparecen en la Vía Láctea.

Siempre, desde los tiempos más remotos y desde que asombrados mirábamos el cielo oscuro y estrellado, nos hemos preguntado por el origen de aquellas maravillas que fascinaba las mentes de los antiguos habitantes de la Tierra y debaja volar su imaginación, quién sabe hacia qué derroteros, si tenemos en cuenta que, los conocimeintos del Universo, eran entonces muy limitados.

Sin embargo, tal ignorancia, no era ningún impedimento para que se llevaran a cabo observaciones exhaustivas y muy precisas e incluso, se levantaran cartas y mapas celestes  que, como cartas astronómicas de la antigüedad, aún algunas perduran como la que arriba podeis contemplar que milagrosamente se ha podido conservar aunque su origen se encuentre en el siglo VII a. C., y, encontrada en una Cueva de Dunhuang, en China, podríamos decir que se trarta del documento astronómico más antiguo que existe, o, al menos, que se conoce.

La astronomía es la más antigua de las ciencias físicas. Se desarrolló en los tiempos antiguos debido a la curiosidad sobre el día y la noche, el sol, la luna, y las estrellas. Por la noche, más de 1000 estrellas visibles seguían un trayecto similar, pareciendo rotar en grupos permanentes, o constelaciones, sobre un punto fijo en el cielo llamado el polo norte celestial. Las primeras inspecciones del cielo fueron anotaciones de las posiciones y los movimientos de las estrellas y los planetas. La gente del Antiguo Egipto, China, América Central y Mesopotamia llevaron a cabo estas inspecciones hace 5000 años.

Los primeros catálogos de posiciones estelares fueron realizados por Shi Shen, Gan De y Wu Xian, los primeros astrónomos notables de China, que trabajaron durante los años 370 a 270 a.C., dos siglos antes de Hiparco. En conjunto sus listas enumeraban 1.464 agrupadas en 284 constelaciones. (Los occidentales hacían grupos más grandes con un total de sólo 88 constelaciones).

                                                    Atlas cometario chino

En el año 310 d.C., durante la dinastía occidental de los Chin (265-317 d.C.), el astrónomo real Qian Luozhi verificó los datos de esta obra temprana, realizando un globo celeste en bronce con las estrellas coloreadas en rojo, negro y blanco para distinguir las listas de los tres astrónomos. Ya en los tiempos de la dinastía Han, los astrónomos preparaban gráficos de estrellas. Las tallas y los relieves muestran constelaciones o asterismos individuales representados mediante puntos o pequeños círculos conectados entre sí por líneas para delinear el conjunto de la constelación en cada caso. Este convenio de utilizar bolitas y segmentos que las unen no apareció en occidente hasta finales del siglo XIX.

Los mapas estelares necesitaban algún medio para especificar las posiciones relativas de los cuerpos celestes, unos con respecto a otros. La ciencia cartográfica dio un salto hacia adelante en el siglo II antes de Cristo, cuando Chang Heng inventó lo que llamamos actualmente cartografía cuantitativa. Chang, un científico puntero inventor del sismógrafo, aplicó un sistema de cuadrículas en los mapas, de tal forma que las posiciones, las distancias y los itirenarios podían calcularse y analizarse. Las obras escritas por el propio Chang Heng se han perdido (como tantos otros tesoros a lo largo de la historia de la humanidad), pero una historia oficial de la dinastía Han afirmaba: “Realizó una red de coordenadas para el cielo y la Tierra, para realizar luego los cálculos basándose en ellas”.

Es una verdadera lástima que nunca se hicieran copias de estos mapas, ya que la información que aparecía en ellos era demasiado peligrosa para arriesgarse a que cayera en manos inadecuadas. Entretanto, en Europa, según dice Robert Temple, la cartografía había degenerado bajo la influencia (nefasta) de la religión “hasta un extremo difícilmente creíble”.

Una de las regiones del planeta que se vio beneficiada con el fin del periodo glacial, fue Mesopotámia (hoy república islámica de Irak), que conservó las condiciones (la fertilidad del suelo y desarrollo agrícola) para continuar el progreso de la civilización sumeria (4.000 aC.). Varias ciudades importantes florecieron entre ellas: Lagash, Kish, Uma, Ur, Uruk, y Eridu , cuyo medio de desarrollo económico se basó en el regadío. En ellas había un rey absoluto el cual se hacia llamar Vicario del dios protector de la ciudad.

Sobre el 3.000 a.C. los sumerios inventan la escritura, en un comienzo pictográfica, pero luego evolucionó a escritura cuneiforme. También inventaron la rueda y los sistemas de medida (longitud, masa, volumen, área) desarrollaron la geometría y una matemática que permitía resolver ecuaciones de hasta tercer grado, estas sin duda, dieron un impulso a su economía.

Mucho es lo que tendremos que aprender del pasado de cuyas reliquias, aún se conservan tesoros que no hemos podido desvelar. Arriba podeis contemplar una tablilla de escritura cuneiforme procedente de Ur. Una de las regiones del planeta que se vio beneficiada con el fin del periodo glacial, fue Mesopotámia (hoy república islámica de Irak), que conservó las condiciones (la fertilidad del suelo y desarrollo agrícola) para continuar el progreso de la civilización sumeria (4.000 aC.). Varias ciudades importantes florecieron entre ellas: Lagash, Kish, Uma, Ur, Uruk, y Eridu , cuyo medio de desarrollo económico se basó en el regadío. En ellas había un rey absoluto el cual se hacia llamar Vicario del dios protector de la ciudad.

Sobre el 3.000 a.C. los sumerios inventan la escritura, en un comienzo pictográfica, pero luego evolucionó a escritura cuneiforme. También inventaron la rueda y los sistemas de medida (longitud, masa, volumen, área) desarrollaron la geometría y una matemática que permitía resolver ecuaciones de hasta tercer grado, estas sin duda, dieron un impulso a su economía.

                                                                                    Tablilla encontrada en Shuruppak, datada en el 2600 a.C.

Ur,  fue el centro principal del culto al dios lunar de la religión sumeria, Nanna, más tarde llamado Sin por los babilonios.  Ur-Nammu (que reinó entre los años 2113 y 2095 a.C.), primer rey de la III Dinastía de Ur, consiguió el control de la salida al mar hacia el 2100 a.C. y convirtió a Ur en la ciudad más rica de Mesopotámia. Su reinado marcó el inicio del denominado renacimiento del arte, la literatura y la ciencia  sumeria. Los descendientes de Ur-Nammu siguieron en el poder durante más de un siglo, hasta el 2003 a.C., cuando los elamitas derrotaron al rey de Ur Ibi-Sin (que reinó entre el 2029 y el 2004 a.C.) y destruyeron la ciudad. Por esa época también caería Babilonia.

Babilonia, fue fundada por Nimrod en 2500 a. C., quizá como un pequeño pueblo sumerio ubicado a orillas de Río Eufrates y subordinado a la más poderosa ciudad de Kish. En 2004 a.C., la ciudad cayó ante la coalición de los pueblos nómadas; Elamitas, y Amorreos. Estos últimos, se asentaron en la Media y Baja Mesopotámia, apoderándose de las ciudades y fundando dinastías amorritas en ellas. La Primer Dinastía Babilónica, fue fundada en 1894 a. C. por el amorrita Sumu-abum y la sexta por el Rey, Hammurabi (que reinó desde 1792 a. C. hasta 1750 a. C.), quien la engrandecería colosalmente y extendería sus dominios, convirtiéndola en la capital del Imperio Amorreo, la cual dominó toda la Mesopotámia. Desde entonces, y en adelante, adquirió gran relevancia como la verdadera metrópoli de todo el sur de Mesopotámia, periodo este  importante en el desarrollo de la  ciencia y  la astronomía.

                                                                                                                                Ruinas de Babilonia

Su interés  por  la búsqueda de presagios permitió adelantos en la astronomía. Evidencias de escrituras realizadas en tablillas de arcilla o piedra,  indican que la práctica astronómica en Babilonia se inicia hacia el año 2500 aC., al denominar constelaciones con nombre de animales reales o imaginarios, conjunto que luego se llamaría Zoodiaco, a sí mismo, le asignaron nombre a las constelaciones constituidas por las estrellas más brillantes.

Hacia el año 1700 a.C. se destaca la adopción del sistema sexagesimal en el cual dividieron el día en 24 horas iguales, las horas en minutos y segundos. Desarrollaron también un calendario, tomando en cuenta el movimiento del Sol y las fases de la Luna (los años  tenían 12 o 13 meses). Este calendario se mantuvo vigente hasta el 500 a.C.

En matemáticas, los sumerios desarrollaron el primer sistema de notación posicional que se conoce. Esto es, un sistema númerico en que cada dígito posee un valor diferente según su posición relativa (no es lo mismo 23 que 32). Este tipo de notación queda definida por la base, que es el número de dígitos necesarios para escribir cualquier número. Por ejemplo; el sistema decimal usa diez números y el binario, dos. Su sistema utilizaba dos símbolos: una cuña apuntando hacia abajo () para representar al uno y otra hacia la izquierda () para el diez. De esta forma, el 15 se escribiría . Colocando un símbolo () más a la izquierda se multiplicaba su valor por 60. Así, 900 (60 15) sería .

Las matemáticas sumerias son el elemento más antiguo de las llamadas Matemáticas Babilónicas, término que se refiere a las matemáticas de la gente de la Mesopotamia en el periodo comprendido entre los sumerios y la caída de Babilonia (539 a. C.), por lo que también incluyen parte de la Edad de hierro. Se denominan así por la importancia de Babilonia como centro de estudio. Entre sus logros están la división del círculo en 360 partes; la división del día en 24 horas, con cada hora de 60 minutos y cada minuto de sesenta segundos; la resolución de ciertos tipos de ecuaciones cuadráticas y cúbicas; el cálculo de raíces utilizando tablas de cuadrados; ¡y el conocimiento del teorema de pitágoras!

                Tablilla con cálculos sobre un reloj de agua

 

 

                                                                                               Zigurat de Ur.

Estamos alrededor del año 3000 a. C. y los avances introducidos por la cultura de Uruk se esparcen por el resto de la Mesopotamia dando nacimiento a la cultura sumeria. La capacidad tecnológica del periodo alentó y permitió un gran desplazamiento de las poblaciones rurales hacia las ciudades; las cuales crecieron, desarrollaron e independizaron de Uruk, quien perdió su hegemonía sobre ellas. Así, la administración regional se abandonó y cada ciudad pasó a tener un gobierno propio, lo cual no implica que unas no fuesen más poderosas e importantes que otras. Las murallas que las rodeaban muestran que, pese a las relaciones comerciales que las vinculaban, estaban en constantes conflictos. Este es el contexto de la época en la que se descubrió la primera aleación: el bronce

Pese a la importancia del uso del bronce en la agricultura y la tecnología militar, el gran logro de la civilización sumeria es ser la primera en desarrollar la escritura: acabamos de entrar en la historia. Como bien se sabe, su sistema era cuneiforme y llegó a contener más de 2000 símbolos distintos. Este se enseñaba en las llamadas «Casas de las tablillas», que aparecieron durante el dominio de Ur, la ciudad más poderosa tras el ocaso de Uruk. Allí era dónde se formaba a los escribas y se preservaba el saber. Solían estar asociadas a un templo o a un palacio, pero también las había privadas para quién podía darse el lujo de pagarlas. Los textos sumerios por excelencia son la narración de Ziusudra y le epopeya de Gilgamesh de la que ya he hablado aquí en otros trababajos.

Los sumerios fundaron la ciudad de Babilonia, que eventualmente sustituiría a Ur como esta sustituyó a Uruk. El rey Hammurabi (1792 – 1750 a.C.), con quién Babilonia alcanzaría su esplendor, fue el primero en levantar un cuerpo de leyes para ejercer la justicia y regular la administración, cosas en las que antes intervenían los clérigos. Como parte de este cuerpo también están las primeras leyes médicas. Algunas de ellas son las siguientes:

• 218. Si un médico (Asu) opera a un noble por una herida grave con una lanceta de bronce y causa la muerte del noble; o si abre un absceso en el ojo de un noble con una lanceta de bronce y lo destruye, se le cortará la mano.
• 219. Si un médico opera a un esclavo con una lanceta de bronce y le causa la muerte, tendrá que reponer el esclavo con otro del mismo valor.
• 221. Si un médico cura una fractura ósea de un noble o alivia una enfermedad de sus intestinos, el paciente le dará cinco shekels (ca. 150 g) de plata al médico.
• 223. Si se trata de un esclavo, el dueño del esclavo le dará dos shekels de plata al médico.

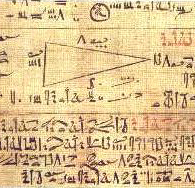
También disponían de un sistema para las fracciones, aunque muy poco práctico. Aun así, en el Museo Británico de Londres puede admirarse el Papiro Rhind (hacia 1650 a.C.) (ver fragmento en figura dcha.), que contiene 87 problemas sobre resolución de ecuaciones, aritmética, geometría, etc.

–   Por su parte, los matemáticos chinos de épocas pasadas ya resolvían sistemas de 3 ecuaciones lineales y 3 incógnitas, como recoge la recopilación Nueve capítulos sobre las artes matemáticas (Jiu zhang suang shu), redactado entre el 200 a.C. y el 200 d.C.

El siglo XIII coincide con la Edad de Oro de la Matemática china. Lichich es autor de un tratado que contiene 170 problemas sobre círculos circunscritos e inscritos en un triángulo. Chiu-Sao resolvía ecuaciones de 2º grado, cúbicas y cuadráticas por un método muy similar al que hoy denominamos «Método de Horner», y calculaba raíces cuadradas. Shih-Chieh sumaba series infinitas y utilizaba el que conocemos como triángulo de Pascal hasta la octava potencia. Pero, después de este período, la Matemática china se estanca, y no podrá equipararse a la occidental.

En el año 600 a.c.Tales, filósofo griego nacido en Mileto introdujo la geometría en Grecia, ciencia que aprendió en Egipto. Sus conocimientos le sirvieron para descubrir importantes propiedades geométricas. Tales no dejó escritos; el conocimiento que se tiene de él procede de lo que se cuenta en la metafísica de Aristóteles.

La Geometría que se sipone nacida en el Antiguop Egipto, alededor del siglo XX antes de nuestra era, de la necesidad de medir los terrenos y realizar construcciones, toma vuelo en Grecia con Tales de Mileto y Pit´çagoras, en el siglo VI antes de nuestra era, cuando comienza a despegarse del pensamiento práctico hacia formas más abstractas. Aquel ciclo culmina con Euclides (370 – 275 a. C.) cuando en su obra elementos con 23 definificiones y 9 asiomas construyó la base lógica de la misma.

Varios siglos después, a inicios del revolucionario siglo XVII, esa geometría elemental recibió un fuerte desarrollo con René Descartes (1596 – 1650) con la creación de la Geometría analítica, emn la que las propiedades de las líneas y los espacios se expresan en ecuaciones. Con Newton (1642 – 1727) y Leibniz (1646 – 1716) quienes crearon los cálculos ininitesimales fue posible incoroprar a la geometría analítica todo tipo de curvas suaves o regulares, como las elípses o las parábolas.

Después de todo aquello, llegamos a geometrías más avanzadas que se podían aplicar a los espacios curvos. Las más conocidas son la geometríam hiperbólica de Lovachevski (1739 – 1836) y la geomet´ria elíptica de Riemann (1826 -1866), las que tomó Einstein para poder formular su Teoría de la Relatividad General.

Es tan importante el pasado que, sin aquellos sabios que nos legaron sus conocimientos, nunca habríamos podido llegar a lo que hoy podemos conocer en Astronomía, Química, Matemáticas…¡Y tántas disciplinas del saber humano! Los antiguos nos regalaron sus brillantes ideas para hacer posible que, en nostros, pudieran brotar otras nuevas a partir de aquellas. ¿Que sería de la Relatividad General sin Riemann? Probablemente nada. Einstein no era precisamente un gran matemático y, hasta que no tuvo en sus manos la célebre conferencia de Riemann, dada sesenta años antes, no pudo formular su teoría por falta de la Geometría adecuada para ello que Riemann le proporcionó y pudo salir de aquel atolladero de más de siete años.

Está claro que, cuando hablamos sobre la contribución que hicieron los pueblos del pasado al saber del mundo, muchos fueron los que aportaron sus granitos de arena (eso sí, unos granos más gosdos que otros) pero, lo cierto es que, todos ellos, de alguna manera, contribuyeron a lo que hoy somos:

¡El presente es el resultado del pasado y, el futuro, estará cargado de nuestro presente!

emilio silvera

[?]