Oct
9
Siempre nos ha interesado mirar hacia el pasado
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del Saber ~
Clasificado en Rumores del Saber ~
 Comments (0)
Comments (0)
Si no fueron los mejores matemáticos astronómicos, los chinos fueron al menos los mejores cartógrafos de estrellas que existieron antes del Renacimiento. Su primer mapa estelar se remonta al menos a 2000 a. C. y se trata de un relieve esculpido en la roca de un barranco en Jiangjunya, en la provincia de Jiangsu. Este relieve contiene numerosas estrellas, así como cabezas humanas y de animales. Hay discos que representan el Sol en posiciones estacionales, donde la Luna y un cierto número de estrellas aparecen a lo largo de las estaciones. Por su posición y su apariencia se puede reconocer que esta zona brillante de la esfera celeste es la Vía Láctea; en el relieve están representados los espacios vacíos y las divisiones que aparecen en la Vía Láctea.
Siempre, desde los tiempos más remotos y desde que asombrados mirábamos el cielo oscuro y estrellado, nos hemos preguntado por el origen de aquellas maravillas que fascinaba las mentes de los antiguos habitantes de la Tierra y debaja volar su imaginación, quién sabe hacia qué derroteros, si tenemos en cuenta que, los conocimeintos del Universo, eran entonces muy limitados.
Sin embargo, tal ignorancia, no era ningún impedimento para que se llevaran a cabo observaciones exhaustivas y muy precisas e incluso, se levantaran cartas y mapas celestes que, como cartas astronómicas de la antigüedad, aún algunas perduran como la que arriba podeis contemplar que milagrosamente se ha podido conservar aunque su origen se encuentre en el siglo VII a. C., y, encontrada en una Cueva de Dunhuang, en China, podríamos decir que se trarta del documento astronómico más antiguo que existe, o, al menos, que se conoce.

La astronomía es la más antigua de las ciencias físicas. Se desarrolló en los tiempos antiguos debido a la curiosidad sobre el día y la noche, el sol, la luna, y las estrellas. Por la noche, más de 1000 estrellas visibles seguían un trayecto similar, pareciendo rotar en grupos permanentes, o constelaciones, sobre un punto fijo en el cielo llamado el polo norte celestial. Las primeras inspecciones del cielo fueron anotaciones de las posiciones y los movimientos de las estrellas y los planetas. La gente del Antiguo Egipto, China, América Central y Mesopotamia llevaron a cabo estas inspecciones hace 5000 años.
Los primeros catálogos de posiciones estelares fueron realizados por Shi Shen, Gan De y Wu Xian, los primeros astrónomos notables de China, que trabajaron durante los años 370 a 270 a.C., dos siglos antes de Hiparco. En conjunto sus listas enumeraban 1.464 agrupadas en 284 constelaciones. (Los occidentales hacían grupos más grandes con un total de sólo 88 constelaciones).

Atlas cometario chino
En el año 310 d.C., durante la dinastía occidental de los Chin (265-317 d.C.), el astrónomo real Qian Luozhi verificó los datos de esta obra temprana, realizando un globo celeste en bronce con las estrellas coloreadas en rojo, negro y blanco para distinguir las listas de los tres astrónomos. Ya en los tiempos de la dinastía Han, los astrónomos preparaban gráficos de estrellas. Las tallas y los relieves muestran constelaciones o asterismos individuales representados mediante puntos o pequeños círculos conectados entre sí por líneas para delinear el conjunto de la constelación en cada caso. Este convenio de utilizar bolitas y segmentos que las unen no apareció en occidente hasta finales del siglo XIX.
Los mapas estelares necesitaban algún medio para especificar las posiciones relativas de los cuerpos celestes, unos con respecto a otros. La ciencia cartográfica dio un salto hacia adelante en el siglo II antes de Cristo, cuando Chang Heng inventó lo que llamamos actualmente cartografía cuantitativa. Chang, un científico puntero inventor del sismógrafo, aplicó un sistema de cuadrículas en los mapas, de tal forma que las posiciones, las distancias y los itirenarios podían calcularse y analizarse. Las obras escritas por el propio Chang Heng se han perdido (como tantos otros tesoros a lo largo de la historia de la humanidad), pero una historia oficial de la dinastía Han afirmaba: “Realizó una red de coordenadas para el cielo y la Tierra, para realizar luego los cálculos basándose en ellas”.
Es una verdadera lástima que nunca se hicieran copias de estos mapas, ya que la información que aparecía en ellos era demasiado peligrosa para arriesgarse a que cayera en manos inadecuadas. Entretanto, en Europa, según dice Robert Temple, la cartografía había degenerado bajo la influencia (nefasta) de la religión “hasta un extremo difícilmente creíble”.
Una de las regiones del planeta que se vio beneficiada con el fin del periodo glacial, fue Mesopotámia (hoy república islámica de Irak), que conservó las condiciones (la fertilidad del suelo y desarrollo agrícola) para continuar el progreso de la civilización sumeria (4.000 aC.). Varias ciudades importantes florecieron entre ellas: Lagash, Kish, Uma, Ur, Uruk, y Eridu , cuyo medio de desarrollo económico se basó en el regadío. En ellas había un rey absoluto el cual se hacia llamar Vicario del dios protector de la ciudad.
Sobre el 3.000 a.C. los sumerios inventan la escritura, en un comienzo pictográfica, pero luego evolucionó a escritura cuneiforme. También inventaron la rueda y los sistemas de medida (longitud, masa, volumen, área) desarrollaron la geometría y una matemática que permitía resolver ecuaciones de hasta tercer grado, estas sin duda, dieron un impulso a su economía.

Mucho es lo que tendremos que aprender del pasado de cuyas reliquias, aún se conservan tesoros que no hemos podido desvelar. Arriba podeis contemplar una tablilla de escritura cuneiforme procedente de Ur. Una de las regiones del planeta que se vio beneficiada con el fin del periodo glacial, fue Mesopotámia (hoy república islámica de Irak), que conservó las condiciones (la fertilidad del suelo y desarrollo agrícola) para continuar el progreso de la civilización sumeria (4.000 aC.). Varias ciudades importantes florecieron entre ellas: Lagash, Kish, Uma, Ur, Uruk, y Eridu , cuyo medio de desarrollo económico se basó en el regadío. En ellas había un rey absoluto el cual se hacia llamar Vicario del dios protector de la ciudad.
Sobre el 3.000 a.C. los sumerios inventan la escritura, en un comienzo pictográfica, pero luego evolucionó a escritura cuneiforme. También inventaron la rueda y los sistemas de medida (longitud, masa, volumen, área) desarrollaron la geometría y una matemática que permitía resolver ecuaciones de hasta tercer grado, estas sin duda, dieron un impulso a su economía.

Tablilla encontrada en Shuruppak, datada en el 2600 a.C.
Ur, fue el centro principal del culto al dios lunar de la religión sumeria, Nanna, más tarde llamado Sin por los babilonios. Ur-Nammu (que reinó entre los años 2113 y 2095 a.C.), primer rey de la III Dinastía de Ur, consiguió el control de la salida al mar hacia el 2100 a.C. y convirtió a Ur en la ciudad más rica de Mesopotámia. Su reinado marcó el inicio del denominado renacimiento del arte, la literatura y la ciencia sumeria. Los descendientes de Ur-Nammu siguieron en el poder durante más de un siglo, hasta el 2003 a.C., cuando los elamitas derrotaron al rey de Ur Ibi-Sin (que reinó entre el 2029 y el 2004 a.C.) y destruyeron la ciudad. Por esa época también caería Babilonia.
Babilonia, fue fundada por Nimrod en 2500 a. C., quizá como un pequeño pueblo sumerio ubicado a orillas de Río Eufrates y subordinado a la más poderosa ciudad de Kish. En 2004 a.C., la ciudad cayó ante la coalición de los pueblos nómadas; Elamitas, y Amorreos. Estos últimos, se asentaron en la Media y Baja Mesopotámia, apoderándose de las ciudades y fundando dinastías amorritas en ellas. La Primer Dinastía Babilónica, fue fundada en 1894 a. C. por el amorrita Sumu-abum y la sexta por el Rey, Hammurabi (que reinó desde 1792 a. C. hasta 1750 a. C.), quien la engrandecería colosalmente y extendería sus dominios, convirtiéndola en la capital del Imperio Amorreo, la cual dominó toda la Mesopotámia. Desde entonces, y en adelante, adquirió gran relevancia como la verdadera metrópoli de todo el sur de Mesopotámia, periodo este importante en el desarrollo de la ciencia y la astronomía.

Ruinas de Babilonia
Su interés por la búsqueda de presagios permitió adelantos en la astronomía. Evidencias de escrituras realizadas en tablillas de arcilla o piedra, indican que la práctica astronómica en Babilonia se inicia hacia el año 2500 aC., al denominar constelaciones con nombre de animales reales o imaginarios, conjunto que luego se llamaría Zoodiaco, a sí mismo, le asignaron nombre a las constelaciones constituidas por las estrellas más brillantes.
Hacia el año 1700 a.C. se destaca la adopción del sistema sexagesimal en el cual dividieron el día en 24 horas iguales, las horas en minutos y segundos. Desarrollaron también un calendario, tomando en cuenta el movimiento del Sol y las fases de la Luna (los años tenían 12 o 13 meses). Este calendario se mantuvo vigente hasta el 500 a.C.
En matemáticas, los sumerios desarrollaron el primer sistema de notación posicional que se conoce. Esto es, un sistema númerico en que cada dígito posee un valor diferente según su posición relativa (no es lo mismo 23 que 32). Este tipo de notación queda definida por la base, que es el número de dígitos necesarios para escribir cualquier número. Por ejemplo; el sistema decimal usa diez números y el binario, dos. Su sistema utilizaba dos símbolos: una cuña apuntando hacia abajo () para representar al uno y otra hacia la izquierda (
) para el diez. De esta forma, el 15 se escribiría
. Colocando un símbolo (
) más a la izquierda se multiplicaba su valor por 60. Así, 900 (60
15) sería
.
Las matemáticas sumerias son el elemento más antiguo de las llamadas Matemáticas Babilónicas, término que se refiere a las matemáticas de la gente de la Mesopotamia en el periodo comprendido entre los sumerios y la caída de Babilonia (539 a. C.), por lo que también incluyen parte de la Edad de hierro. Se denominan así por la importancia de Babilonia como centro de estudio. Entre sus logros están la división del círculo en 360 partes; la división del día en 24 horas, con cada hora de 60 minutos y cada minuto de sesenta segundos; la resolución de ciertos tipos de ecuaciones cuadráticas y cúbicas; el cálculo de raíces utilizando tablas de cuadrados; ¡y el conocimiento del teorema de pitágoras!
Estamos alrededor del año 3000 a. C. y los avances introducidos por la cultura de Uruk se esparcen por el resto de la Mesopotamia dando nacimiento a la cultura sumeria. La capacidad tecnológica del periodo alentó y permitió un gran desplazamiento de las poblaciones rurales hacia las ciudades; las cuales crecieron, desarrollaron e independizaron de Uruk, quien perdió su hegemonía sobre ellas. Así, la administración regional se abandonó y cada ciudad pasó a tener un gobierno propio, lo cual no implica que unas no fuesen más poderosas e importantes que otras. Las murallas que las rodeaban muestran que, pese a las relaciones comerciales que las vinculaban, estaban en constantes conflictos. Este es el contexto de la época en la que se descubrió la primera aleación: el bronce
Pese a la importancia del uso del bronce en la agricultura y la tecnología militar, el gran logro de la civilización sumeria es ser la primera en desarrollar la escritura: acabamos de entrar en la historia. Como bien se sabe, su sistema era cuneiforme y llegó a contener más de 2000 símbolos distintos. Este se enseñaba en las llamadas «Casas de las tablillas», que aparecieron durante el dominio de Ur, la ciudad más poderosa tras el ocaso de Uruk. Allí era dónde se formaba a los escribas y se preservaba el saber. Solían estar asociadas a un templo o a un palacio, pero también las había privadas para quién podía darse el lujo de pagarlas. Los textos sumerios por excelencia son la narración de Ziusudra y le epopeya de Gilgamesh de la que ya he hablado aquí en otros trababajos.
Los sumerios fundaron la ciudad de Babilonia, que eventualmente sustituiría a Ur como esta sustituyó a Uruk. El rey Hammurabi (1792 – 1750 a.C.), con quién Babilonia alcanzaría su esplendor, fue el primero en levantar un cuerpo de leyes para ejercer la justicia y regular la administración, cosas en las que antes intervenían los clérigos. Como parte de este cuerpo también están las primeras leyes médicas. Algunas de ellas son las siguientes:
- 218. Si un médico (Asu) opera a un noble por una herida grave con una lanceta de bronce y causa la muerte del noble; o si abre un absceso en el ojo de un noble con una lanceta de bronce y lo destruye, se le cortará la mano.
- 219. Si un médico opera a un esclavo con una lanceta de bronce y le causa la muerte, tendrá que reponer el esclavo con otro del mismo valor.
- 221. Si un médico cura una fractura ósea de un noble o alivia una enfermedad de sus intestinos, el paciente le dará cinco shekels (ca. 150 g) de plata al médico.
- 223. Si se trata de un esclavo, el dueño del esclavo le dará dos shekels de plata al médico.
Parte superior de una estela de diorita que contiene las 282 leyes del código de Hammurabi. La estela mide 2,25 metros de altura y contiene una representación Hammurabi en bajorrelieve (de pie) delante del dios del Sol de Mesopotamia, Shamash.
Como la propia Civilización egipcia, la historia de las matemáticas en Egipto es larga, dado que comienza el año 3200 a. C., cuando se inventó un sistema de escritura, y se alarga hasta erl año 332 a.C., cuando Alejandro Magno conquistí y helenizó Egipto. Las fuentes son escasas porque el papiro se deteriora en un medio ambiente húmedo. Los únicos documentos legibles son los hallados en los cementerrios y templos de la franja desértica situada a lo largo del Valle del Nilo. Pocos son los papiros recuperados procedentes de pueblos o ciudades importantes de las áreas fértiles ubicadas en la zina del Nilo o en su delta.
El papiro de Rhind es el documento más antiguo de la matemática egipcia -y tal vez de todo el pensamiento matemático- realizado en el año 650 a.n.e. es copia de otro anterior, que data aproximadamente del año 2000 a.n.e., en él puede observarse el dibujo de un triángulo y anotaciones sobre el mismo)
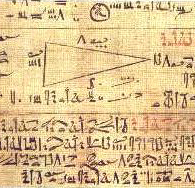
También disponían de un sistema para las fracciones, aunque muy poco práctico. Aun así, en el Museo Británico de Londres puede admirarse el Papiro Rhind (hacia 1650 a.C.) (ver fragmento en figura dcha.), que contiene 87 problemas sobre resolución de ecuaciones, aritmética, geometría, etc.
– Por su parte, los matemáticos chinos de épocas pasadas ya resolvían sistemas de 3 ecuaciones lineales y 3 incógnitas, como recoge la recopilación Nueve capítulos sobre las artes matemáticas (Jiu zhang suang shu), redactado entre el 200 a.C. y el 200 d.C.
El siglo XIII coincide con la Edad de Oro de la Matemática china. Lichich es autor de un tratado que contiene 170 problemas sobre círculos circunscritos e inscritos en un triángulo. Chiu-Sao resolvía ecuaciones de 2º grado, cúbicas y cuadráticas por un método muy similar al que hoy denominamos «Método de Horner», y calculaba raíces cuadradas. Shih-Chieh sumaba series infinitas y utilizaba el que conocemos como triángulo de Pascal hasta la octava potencia. Pero, después de este período, la Matemática china se estanca, y no podrá equipararse a la occidental.
En el año 600 a.c.Tales, filósofo griego nacido en Mileto introdujo la geometría en Grecia, ciencia que aprendió en Egipto. Sus conocimientos le sirvieron para descubrir importantes propiedades geométricas. Tales no dejó escritos; el conocimiento que se tiene de él procede de lo que se cuenta en la metafísica de Aristóteles.
La Geometría que se sipone nacida en el Antiguop Egipto, alededor del siglo XX antes de nuestra era, de la necesidad de medir los terrenos y realizar construcciones, toma vuelo en Grecia con Tales de Mileto y Pit´çagoras, en el siglo VI antes de nuestra era, cuando comienza a despegarse del pensamiento práctico hacia formas más abstractas. Aquel ciclo culmina con Euclides (370 – 275 a. C.) cuando en su obra elementos con 23 definificiones y 9 asiomas construyó la base lógica de la misma.
Varios siglos después, a inicios del revolucionario siglo XVII, esa geometría elemental recibió un fuerte desarrollo con René Descartes (1596 – 1650) con la creación de la Geometría analítica, emn la que las propiedades de las líneas y los espacios se expresan en ecuaciones. Con Newton (1642 – 1727) y Leibniz (1646 – 1716) quienes crearon los cálculos ininitesimales fue posible incoroprar a la geometría analítica todo tipo de curvas suaves o regulares, como las elípses o las parábolas.

Después de todo aquello, llegamos a geometrías más avanzadas que se podían aplicar a los espacios curvos. Las más conocidas son la geometríam hiperbólica de Lovachevski (1739 – 1836) y la geomet´ria elíptica de Riemann (1826 -1866), las que tomó Einstein para poder formular su Teoría de la Relatividad General.

Es tan importante el pasado que, sin aquellos sabios que nos legaron sus conocimientos, nunca habríamos podido llegar a lo que hoy podemos conocer en Astronomía, Química, Matemáticas…¡Y tántas disciplinas del saber humano! Los antiguos nos regalaron sus brillantes ideas para hacer posible que, en nostros, pudieran brotar otras nuevas a partir de aquellas. ¿Que sería de la Relatividad General sin Riemann? Probablemente nada. Einstein no era precisamente un gran matemático y, hasta que no tuvo en sus manos la célebre conferencia de Riemann, dada sesenta años antes, no pudo formular su teoría por falta de la Geometría adecuada para ello que Riemann le proporcionó y pudo salir de aquel atolladero de más de siete años.
Está claro que, cuando hablamos sobre la contribución que hicieron los pueblos del pasado al saber del mundo, muchos fueron los que aportaron sus granitos de arena (eso sí, unos granos más gosdos que otros) pero, lo cierto es que, todos ellos, de alguna manera, contribuyeron a lo que hoy somos:
¡El presente es el resultado del pasado y, el futuro, estará cargado de nuestro presente!
emilio silvera
Oct
8
La relatividad especial
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Relatiovidad Especial ~
Clasificado en Relatiovidad Especial ~
 Comments (2)
Comments (2)
En cualquier parte que podamos buscar información nos dirán:
“Henri Poincqaré, matemático francés, sugirió a finales del siglo XIX que el principio de relatividad establecido desde Galileo (la invariancia galileana) se mantiene para todas las leyes de la naturaleza. Joseph Larmor y Hendrik Lorentz descubrieron que las ecuaciones de Maxwell, la piedra angular del electromagnetismo, eran invariantes solo por una variación en el tiempo y una cierta unidad longitudinal, lo que produjo mucha confusión en los físicos, que en aquel tiempo estaban tratando de argumentar las bases de la teoría del éter, la hipotética substancia sutil que llenaba el vacío y en la que se transmitía la luz. El problema es que este éter era incompatible con el principio de relatividad.
En su publicación de 1905 en electrodinámica, Henri Poincaré y Albert Einstein explicaron que, con las transformaciones hechas por Lorentz, este principio se mantenía perfectamente invariable. La contribución de Einstein fue el elevar a este axioma a principio y proponer las transformaciones de Lorentz como primer principio. Además descartó la noción de tiempo absoluto y requirió que la velocidad de la luz en el vacío sea la misma para todos los observadores, sin importar si éstos se movían o no. Esto era fundamental para las ecuaciones de Maxwell, ya que éstas necesitan de una invarianza general de la velocidad de la luz en el vacío.”

Como en otras ocasiones, aquí dejamos una muestra de la velocidad de la luz cuando viaja desde la Tierra a la Luna
La aparición de la Teoría de la relatividad fue tan poco convencional como su autor. El ya famoso artículo que escribió en 1905 (con el apoyo de los trabajos de los arriba mencionados) y que enunciaba por primera vez la teoría, era algo rústico y sencillo y no mencionaba o contenía cita científico-literaria alguna, tampoco mencionaba ayuda de ninguna persona a excepción de su amigo Besso, que dicho sea de paso no era científico (él, por aquel entonces, no conocía a científico alguno). La primera conferencia de Einstein explicando la Teoría, en Zurich, no fue dada en ninguna universidad sino en el salon del Sindicato de Carpinteros, duró más de una hora, y luego repentinamente se interrumpió para preguntar la hora, explicando que no tenía reloj. Sin embargo, a pesar de los modestos comienzos, allí comenzó a reformarse los conceptos del espacio y del tiempo.

Lo cierto es que, con su teoría de la relatividad, Einstein finalmente resolvió la paradoja que se había presentado a los dieciseis años, por la que las ecuciaones de Maxwell pierden su validez si uno atrapa un haz de luz a la velocidad de la luz. Lo hizo mediante la conclusión de que no se puede acelerar la velocidad de la luz, de que la velocidad de la luz es la misma para todos los observadores, cualquiera que sea su movimiento relativo. Si un astronáuta que vuela hacia la estrella más cercana a una velocidad del cincuenta por ciento de la de la luz, , midiera la velocidad de la luz a bordo de la nave, el resultado sería exactamente igual que el que daría la medición de otro colega suyo situado en la Tierra.

Diferentes sistemas de referencia para el mismo fenómeno. Claro que, en la teoría están presentes factores y trabajos que no se mencionan y, la fórmula siguiente:  es el llamado factor de Lorentz donde
es el llamado factor de Lorentz donde  es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa
es la velocidad de la luz en el vacío. Contrario a nuestro conocimiento actual, en aquel momento esto era una completa revolución, debido a que se planteaba una ecuación para transformar al tiempo, cosa que para la época era imposible. En la mecánica clásica, el tiempo era un invariante. Y para que las mismas leyes se puedan aplicar en cualquier sistema de referencia se obtiene otro tipo de invariante a grandes velocidades (ahora llamadas relativistas), la velocidad de la luz. Los sucesos que se realicen en el sistema en movimiento S’ serán más largos que los del S. La relación entre ambos es esa  . Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
. Este fenómeno se lo conoce como dilatación del tiempo. Si se dice que el tiempo varía a velocidades relativistas, la longitud también lo hace.
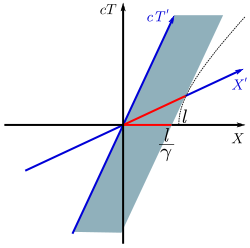
En el gráfico se escenifica la contracción de Lorentz
Para cuantificar aquella extraña situación, Einstein se vio obligado a emplear la contracción de Lorentz (En aquel momento no conocía a Lorentz al que más tarde consideraría “el hombre más grande y más noble de nuestro tiempo… una obrta de arte viviente.)” En manos de Einstein, las ecuciones de Lorentz esopecifican que, cuando aumenta la velocidad a la que se desplaza un observador, sus dimensiones, y la de la nave espacial y todo aparato de medición que haya a bordo, se contrae a lo largo de su movimiento en la cantidad requerida para hacer que la medición de la velocidad de la luz sea siempre la misma.
Esta era la razón de que Michelson y Morley no hallasen ningún rastrodel “arrastre del éter”. En verdad, el éter es superfluo, al igual que el espacio y el tiempo absolutos de Newton, pues no hay ninguna necesidad de un marco de referencia inmóvil. “Al concepto de reposo absoluto no le corresponde ninguna propiedad de los fenómenos, ni en la mecánica ni en la electromecánica.” Lo importante son los sucesos observables, y no puede observarse ningún suceso hasta que la luz (o las ondas de radio o cualquier otra forma de radiación electromagnética) que lleve noticias de él no llegue al observador. Einstein reemplazó el espacio de Newton por una red de haces de luz; la de ellos era una red absoluta dentro de la cual el espacio mismo se vuelve flexible.

Los observadores en movimiento experimentan también una lentificación del paso del tiempo. Un astronáuta que viaje al 90 por 100 de la velocidad de la luz sólo envejecerá a la mitad de rápido que su colega de la Tierra. Ya conocéis la paradoja de los gemelos en la que se explica tal fenómeno.

También en aquel primer artículo Einstein nos habló sobre la igualdad entre la masa y la energía. Él demostró que la masa de un cuerpo aumenta cuando absorbe energía. Se sigue de ello que su masa disminuye cuando irradia energía. Esto es verdadero no sólo para una nave espacial que se desplaza hacia las estrellas, sino también para un objeto en reposo. Una máquina fotográfica pierde algo (muy poco) de masa cuando el flash se dispara, y la gente cuya fotografía se saca se vuelve también, un poco más masiva al absorber sus cuerpos aquella radiación perdida por la máquina. Masa y energía son intercambiables.
m = E/c2
donde m es la masa del objeto, E su energía y c la velocidad de la luz. Al formular esta ecuación particularmente sencilla, que unifica los conceptos de energía y materia, y relaciona ambos con la velocidad de la luz, Einstein inicialmente estaba interesado en la masa. En cambio, si despejamos la energía, adquiere una forma más familiar y presagiosa:
en la Isla de los Museos (Berlín). Festejando el Año mundial de la Física en 2005, en el centenario de la publicación de la ecuación más famosa del mundo. Contemplada desde esta perspectiva, la teoría dice que la materia es energía congelada. Esto, por supuesto, es la clave de la fuerza nuclear y, en manos de los astrofísicos, la ecuación sería usada para descubrir los procesos termonucleares en el corazón de las estrellas.
Pero pese a todos sus variados logros, la relatividad especial no decía nada de la gravitación y, su autor, la veía incompleta. Aquella teoría sin la presencia de la otra gran fuerza más conocida del universo se veíoa desvalída: Había que vincularla con la masa inercial. La resistencia al cambio que ofrecen los objetos en estado de movimiento, su “peso” por decirlo así. La gravitación actúa sobre los objetos según su masa gravitacional, esto es, su “peso”. Todos sabem,os lo que es la masa inercial y de ella, tendremos que hablar cuando acometamos la p´çagina sobre la relatividad general. Dejemos aquí el apunte de que, la masa inercial y la gravitación de cualquier objeto son iguales. También se podría decir que, es la masa de los cuerpos que pueblan el universo, la que moldea y modela la geometría del del Cosmos, del espacio-tiempo.

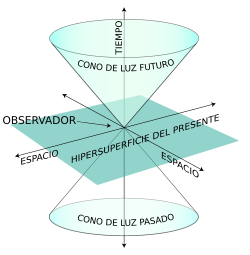
Terminemos con la misma imagen del comienzo. Causalidad e imposibilidad de movimientos más rápidos que la luz. Previo a esta teoría, el concepto de causalidad estaba determinado: para una causa existe un efecto. Anteriormente, gracias a los postulados de Laplace, se creía que para todo acontecimiento se debía obtener un resultado que podía predecirse. La revolución en este concepto es que se “crea” un cono de luz de posibilidades (Véase gráfico adjunto).
Se observa este cono de luz y ahora un acontecimiento en el cono de luz del pasado no necesariamente nos conduce a un solo efecto en el cono de luz futuro. Desligando así la causa y el efecto. El observador que se sitúa en el vértice del cono ya no puede indicar qué causa del cono del pasado provocará el efecto en el cono del futuro.
Asumiendo el principio de causalidad obtenemos que ninguna partícula de masa positiva puede viajar más rápido que la luz. A pesar que este concepto no es tan claro para la relatividad general. Pero no solo el principio de causalidad imposibilita el movimiento más rápido que el de la luz. Ya hablaremos de ello.
emilio silvera
Oct
7
¡Los Físicos! Algunas veces poetas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)
Masa-Energía-Materia-Luz: Todo la misma cosa:
¡El Universo!
Un apunte que sea un… Preludio a la relatividad
-Las ecuaciones de Lorentz-Fitzgerald-
En 1893, el físico irlandés George Francis FitzGerald emitió una hipótesis para explicar los resultados negativos del experimento conocido de Michelson-Morley. Adujo que toda materia se contrae en la dirección del movimiento, y que esa contracción es directamente proporcional al ritmo (velocidad) del movimiento.
Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso. Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.
Oct
6
¡El Universo! ¿Nuestra casa?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (5)
Comments (5)
Como nos dice la filosofía, nada es como se ve a primera vista, todo depende bajo el punto de vista desde en el que miremos las cosas. Considerar el Universo como nuestra casa, podría considerarse algo egocéntrico, toda vez que, podrá ser la casa de muchos que lo mismo que nosotros, encontraron un lugar idóneo para evolucionar a partir de la materia inerte que, según creo, es menor inerte de lo que podríamos pensar.

Dos galaxias cuajadas de estrellas y mundos que, sin remedio, se encaminan hacia su final individual. En unos pocos millones de años formaran una gran galaxia elíptica. ¿Qué pasará con los mundos y las criaturas que allí residen? Claro que, podrían escapar a universos paralelos.
“Lo primero que hay que comprender sobre los universos paralelos… es que no son paralelos. Es importante comprender que ni siquiera son, estrictamente hablando, universos, pero es más fácil si uno lo intenta y lo comprende un poco más tarde, después de haber comprendido que todo lo que he comprendido hasta ese momento no es verdadero.”
Douglas Adams
¿Qué vamos a hacer con esta idea antrópica fuerte? ¿Puede ser algo más que una nueva presentación del aserto de que nuestra forma de vida compleja es muy sensible a cambios pequeños en los valores de las constantes de la naturaleza? ¿Y cuáles son estos “cambios”? ¿Cuáles son estos “otros mundos” en donde las constantes son diferentes y la vida no puede existir?
En ese sentido, una visión plausible del universo es que hay una y sólo una forma para las constantes y leyes de la naturaleza. Los universos son trucos difíciles de hacer, y cuanto más complicados son, más piezas hay que encajar. Los valores de las constantes de la naturaleza determinan a su vez que los elementos naturales de la tabla periódica, desde el hidrógeno número 1 de la tabla, hasta el uranio, número 92, sean los que son y no otros. Precisamente, por ser las constantes y leyes naturales como son y tener los valores que tienen, existe el nitrógeno, el carbono o el oxígeno.
Oct
5
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
![]()
Icono conmemorativo del Primer Concilio de Nicea
Los cristianos calculaban la edad del mundo consultando las cronologías bíblicas de los nacimientos y muertes de los seres humanos, agregando los “engendrados”, como decían ellos. Este fue el método de Eusebio que presidió el Concilio de Nicea convocado por el emperador Constantino en 325 d. C. para definir la doctrina cristiana, y quien estableció que habían pasado 3.184 años entre Adan y Abraham; de san Agustin de Hipona, que calculó la fecha de la Creación en alrededor del 5500 a.C.; de Kepler, que la fechó en 3993 a.C.; y de Newton, que llegó a una fecha sólo cinco años anterior a la de Kepler. Su apoteosis llegó en el siglo XVII, cuando James Ussher, obispo de Armagh, Irlanda, llegó a la conclusión de que “el comienzo del tiempo… se produjo al comienzo de la noche que precedió al día 23 de octubre del año… 4004 a.C.”.
Pasado el tiempo, la exactitud de Ussher le convirtió en el blanco de las burlas de muchos eruditos modernos, pero, a pesar de todos sus absurdos, su enfoque -y, más en general, el enfoque cristiano de la historiografía- hizo más para estimular la investigación científica del pasado que el altanero pesimismo de los griegos. Al difundir la idea de que el universo tuvo un comienzo en erl tiempo y que, por lo tanto, la edad de la Tierra era finita y medible, los cronólogos cristianos montaron sin saberlo el escenario para la época de estudio científico de la cronología que siguió.

Georges Louis Leclerc, Conde de Buffon (Montbard, 7 de septiembre de 1707 – París, 16 de abril de 1788) fue un naturalista, botánico, matemático, biólogo, cosmólogo y escritor francés.
Claro que, la diferencia estaba en que los científicos no estudiaban las Escrituras, sino las piedras. Así fué como el naturalista que arriba podeis ver, expresaba el credo de los geólogos en 1778:
““Así como en la historia civil consultamos documentos, estudiamos medallones y desciframos antiguas inscripciones, a fin de establecer las épocas de las revoluciones humanas y fijar las fechas de los sucesos morales, así también en la historia natural debemos excavar los archivos del mundo, extraer antiguas reliquias de las entrañas de la tierra [y] reunir sus fragmentos… Este es el único modo de fijar ciertos puntos en la inmensidad del espacio, y colocar una serie de mojones en el camino eterno del tiempo.”
Abraham Gottlob Werner (1749 o 1750–1817) fue un científico alemán.
Entre los primeros que aprendieron a leer el lenguaje de las piedras estaban Abraham Gottlob, un geólo alemán, y William Smith, un inglés inspector de canales e ingeniero asesor que colaboró en la excavación del canal del carbón de Somersetshire en 1793, Werner observó que los mismos estratos podían hallarse en el mismo orden en lugares muy alejados unos de otros, lo cual indicaba que el mecanismo que los había formado había operado a gran escala. Esto implicaba que los estratos locales podían brindar elementos de juicio sobre cómo había cambiado el planeta como un todo. Smith, por su parte, observó que los estratos -dispuestos, según sus palabras, como “rebanadas de pan con mantequilla”- no sólo podían ser identificados por su composición total, sino también por las diversas clases de fósiles que contenían.

¿Son los fósiles un exponente universal de la evolución? ¿Cuál es el verdadero mensaje del registro estratigráfico de la tierra y de los fósiles incorporados en el mismo? El registro fósil podría ser la piedra de toque de la teoría de la evolución.
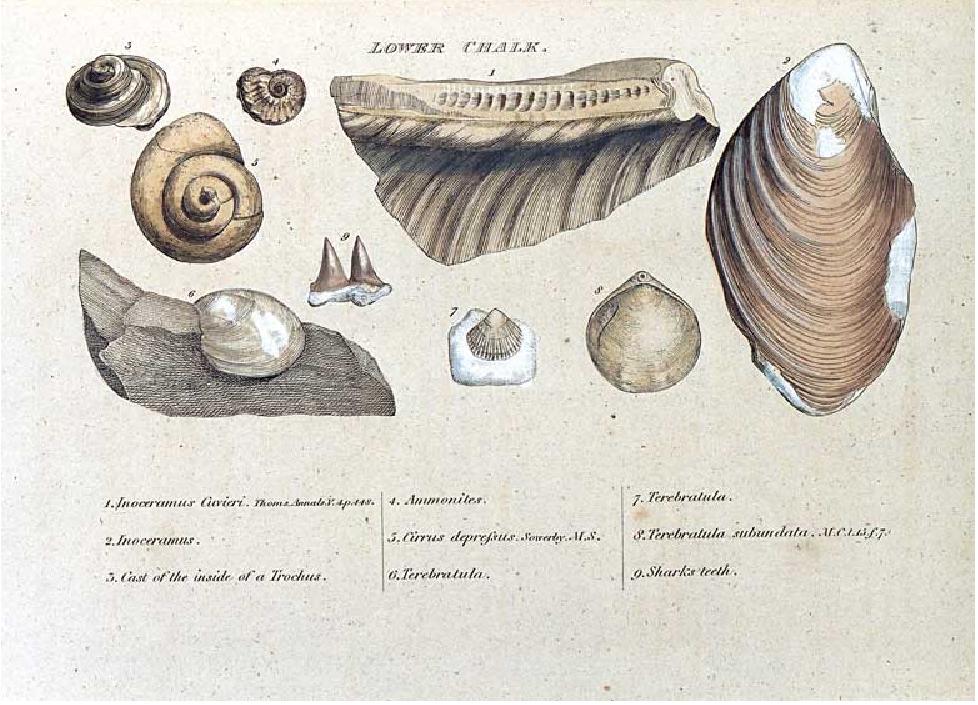
Grabado de la histórica monografía de William Smith, 1815, que dio impulso a la práctica de la correlación de estratos por los fósiles que contienen.
A partir de aquí la búsqueda de huellas del pasado se convirtió en una actividad desaforada y el registro fósil pronto empezó a ofrecer testimonio de seres que ya no se encontraban en el mundo actual. La ausencia de sus equivalentes vivos era un reto a los defensores de la versión bíblica de la historia, que afirmaba, basándose en las Escrituras, que todos los animales fueron creados al mismo tiempo y que ninguna especie se había extinguido desde entonces. A medida que pasaron los años se exploraron cada vez más profundamente las soledades del mundo y las listas de las especies que faltabn era cada vez más larga; George Cuvier, el zoólogo francés que fundó la ciencia de la paleontología, en 1801 había identificado veintitres especies de animales extinguidos en el registro fósil, y la palabra “extinguido” empezó a sonar como una campana que toca a muerto en la literatura científica y las salas universitarias. Ha seguido tocando a muerto desde entonces, y hoy se admite que el 99 por 100 de todas las especies que han vivído sobre la Tierra han desaparecido.

Casi igualmente problemática para los interpretes cristianos de la historia de la Tierra fue la desconcertante variedad de especies vivientes que los biólogos descubrían en sus laboratorios y los naturalistas al explorar las junglas de África, América del Sul y el sureste de Asia. Algunas, como los escarabajos subtropicales gigantes que mordieron al joven Darwin, eran dañinas; sus beneficios para la humanidad, para la que decía que Dios había hecho el mundo, no era evidente. Muchas eran las minúsculas que sólo podían ser detectadas con un microscopio; su papel en el plam de Dios no había sido previsto. Otras eran instintivamente inquietantes, y ninguna más que el orangután, cuyo nombre deriva de la voz malaya que significa “hombre salvaje”, y cuya mirada cálida yn casi íntima, al provenir de una especie muy cercana a la humana en la reserva genética de los primates, parecía burlarse de la pretensión de esta última de ser única.

Si se creía que ninguno de estos seres aparecía en las listas de pasajeros del Arca de Noé… ¿Qué hacían aquí? La ortodoxia religiosa se refugió temperalmente en el concepto de una “gran cadena del ser”. Éste sostenía que la jerarquía de los seres vivos, desde los más elementales microorganismos hasta los monos superiores y las grandes ballenas, habían sido creados por Dios simultáneamente, y que todos juntos formaban una maravillosa estructura, una montaña mágica, con los seres humanos en – o cerca de – su cúspide.
Es difícil sobrestimar la importancia de la gran cadena del ser en el pensamiento del siglo XVIII; figuraba en la estructura de la mayoría de las hipótesis científicas de la época. Pero la cadena no era más fuerte que su eslabón más débil; su mismo carácter completo era una prueba de la perfección de Dios y, por consiguiente, no podía haber ningún “eslabón perdido”. (El término adoptado luego por los evolucionistas proviene de aquí.) Como escribió John Locke:
“En todo el mundo corpóreo visible no vemos simas o abismos. Toda la escala descendente a partir de nosotros es muy gradual, es una serie continua que en cada paso difiere muy poco del anterior. Hay peces que tienen alas y no son extraños al aire, y hay algunos pájaros que son habitantes del agua, cuya sangre es tan fría como la de los peces… Cuando consideramos el poder y la sabiduría infinitos del Hacedor, tenemos razones para pensar que es propio de la magnifica armonía del universo, y al gran designio e infinita bondad de su arquitecto, que las especies de seres asciendan, en suaves transiciones, desde nosotros hacia su infinita perfección, como vemos que desdcienden gradualmente a partir de nosotros.”

Ellos reinaron en nuestro mundo durante unos 150 millones de años. Nosotros hemos llegado aquí, como aquel que dice, antes de ayer pero, “racionales” al fin y al cabo, queremos dolucidar todo lo que, desde los comienzos, pudo pasar y, para ello, el mejor camino será el de la ciencia, ya que, la religión, no puede emitir veredictos fehacientes y, en lugar de basarse en las pruebas, lo hace en la fe que, desde luego, no ofrece ninguna garantía de que lo que afirma, sea lo que en realidad se ajuste a la historia que buscamos saber. Ya sabeis, aquel obispo decía que… “el comienzo del tiempo… se produjo al comienzo de la noche que precedió al día 23 de octubre del año… 4004 a.C.”.
Bueno, no me río pero no por falta de ganas sino por respeto hacia la persona que emitió aquellas palabras y, en consideración al tiempo y al contexto donde las mismas fueron pronunciadas. Lo penoso es que ahora, después de pasados algunos siglos, existan personas que siguen erre que erre insistiendo en los mismos errores. Parece que el tiempo no pasa para ellos y se aferran a unos argumentos “divinos” de trasnochados pensamientos que, alejados de la realidad científica sólo nos pueden conducir hacia la confusión.
emilio silvera
















 Totales: 75.611.182
Totales: 75.611.182 Conectados: 56
Conectados: 56




























