Oct
1
¿Cuándo nos daremos cuenta?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia debe avanzar ~
Clasificado en La Ciencia debe avanzar ~
 Comments (0)
Comments (0)
Sí, ¿cuando nos daremos cuenta de que, el futuro mismo de la Humanidad, depende directamente de lo que hagamos en el campo de la Ciencia? Son las distintas disciplinas del saber Humano las que deben avanzar para ir buscando las soluciones que necesitamos para cubrir, todas nuestras necesidades que, cada día, con el crecimiento imparable de la población mundial, son más y más exigentes.

Se ha reunido el Consejo de Investigación y han denunciado la resistencia política a invertir en la Investigación y conceder subvenciones a proyectos científicos encaminados al avance de la Humanidad. Todos los Científicos del Mundo quieren y desean que se produzca un gran impulso en este campo que, como sabemos y a pesar de lo que muchos creen, es la hermana pobre de las inversiones, ya que, lo que prima son los resultados inmediatos que, en Ciencia, están ausentes..
Los intereses especuladores de los Mercados y la irresponsababilidad e incompetencia de los políticos, han hecho posible que estemos situados en este lugar en el que, muchos son los que sufren y, la Ciencia, no podía ser una excepción.

En una situación de crisis como la actual, y cuando lo que está en cuestión son las inversiones dedicadas a la investigación, cualquier esfuerzo para mejorarlas, o por lo menos preservarlas, no es en vano. Así lo ha entendido el Consejo Europeo de Investigación (ERC , según sus siglas en inglés), una agencia dirigida por científicos fundada en 2007 dentro del 7º Programa Marco de Investigación. En su última reunión, celebrada recientemente en Barcelona, ha actuado de portavoz de la comunidad científica europea, que ha sacado todo su músculo para tratar de hacer ver a los burócratas de Bruselas y de los Estados miembros la necesidad de seguir la vía de éxito que puede situar a Europa en la misma liga que juega Estados Unidos: la de la excelencia científica. Consolidar el ERC como una estructura fija de financiación científica que solo tenga en cuenta la excelencia y no la nacionalidad es ahora el objetivo para disponer de un instrumento de política científica a escala europea.

Parece que en Estados Unidos, la Ciencia camina por otro sendero diferente al de Europa, y, allí, a pesar de todo, su Presidente sí se reune y escucha a los científicos que le ponen al día de lo que interesa a todos.
Homenaje a la ciencia por parte del presidente de los EEUU, donde explica la importancia que ésta tiene como fuente de conocimiento y motor de la economía. Interesante su mensaje: “los políticos debemos escuchar los mensajes de los científicos, aunque éstos no sean complacientes, especialmente cuando no sean complacientes”. Un buen discurso para ser escuchado un 12 de febrero, el día del cumpleaño de Charles Darwin.
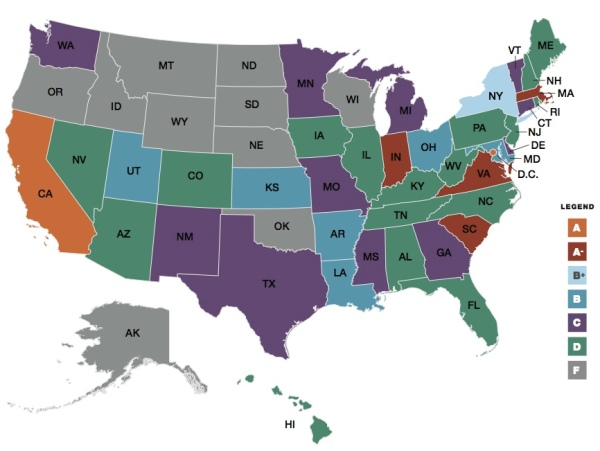
El presente mapa presenta el resultado de la evaluación realizada por el Instituto Fordham sobre estado de las ciencias en EEUU, representado por estados y calificado desde la A (máxima posible) a F (la peor posible). Juzgar por vosotros mismos.
Mientras tanto La Academia Europea, dio la visión de los científicos sobre el ERC y dijo que habían sido muy bienvenidas en la comunidad científica sus subvenciones. Este entusiasmo no ha sido compartido, o al menos al mismo nivel, por los políticos y burócratas, europeos o de los organismos nacionales de investigación. Más de 900 científicos y universitarios de instituciones españolas reivindican el pensamiento crítico en un manifiesto que presentan hoy en Madrid, en un acto que se celebrará en el Consejo Superior de Investigaciones Científicas (CSIC).
– Hasta la fecha, el Consejo Europeo de Investigación (ERC) ha financiado 1.069 proyectos a jóvenes científicos y a investigadores consolidados. Su presupuesto para los primeros siete años de actividad asciende a 7.500 millones de euros.

Claro que, en Estados Unidos siempre parecen ir algunos pasos por delante: Genetistas estadounidenses anunciaron hoy que han producido por primera vez una célula controlada por ADN elaborado por el ser humano, un paso que acerca la ciencia a la creación de vida artificial.
Esta es la primera especie autoduplicable que existe en el planeta cuyo padre es un ordenado. Desde hace décadas científicos de todo el mundo manipulan algunos genes de animales y plantas, pero es la primera vez que alguien cambia el genoma completo.
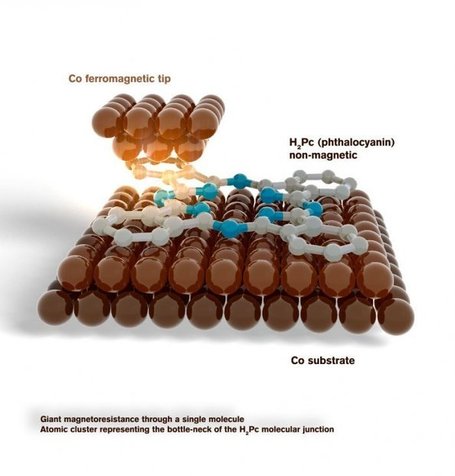
Claro que también, se está avanzando, a pesar de todo en los otros ámbitos de la Ciencia y, no sólo los científicos hacen que eso sea así, algunos, aportamos un granito de arena con nuestras humildes aportaciones. La Imagen de arriba la encontré repasando por ahí y estaba en un artículo mío: El “universo” de lo muy pequeño: NANO : Blog de Emilio Silvera V.
No será posible que la Ciencia avance si no ponemos el remedio para que ello suceda y, debemos comenzar por la enseñanza en la que, desgraciadamente, están sólidamente establecidos conceptos caducos que, amntienen a una clase de “científicos” que, al no tener los suficientes alicientes para que los cambios sde produzcan (podrían ser nefastos para ellos), dejan que el tiempo transcurra y que todo siga igual. Lo pagan los jóvenes estudiantes de Ciencia que, de esta manera, quedan abocados a un retroso en el progreso que no podemos consentir.

Me alegra leer: “Expertos de todo el mundo diseñan un colisionador de partículas lineal para desvelar los grandes misterios del universo”. Los físicos se han cansado de dar rodeos. Durante el último cuarto de siglo han utilizado máquinas circulares, cada vez de mayor tamaño, con las que aclarar cómo surgió el universo tras el Big Bang. Estas máquinas redondas y kilométricas, donde giran partículas subatómicas rozando la velocidad de la luz, han dado hallazgos claves y aún se espera de ellas descubrimientos dignos de un Nobel. Sin embargo, los físicos del mundo lo tienen claro: la próxima gran máquina debe ser recta.
Los expertos denominan a este nuevo gran laboratorio acelerador de partículas lineal. Será el sucesor del Gran Colisionador de Hadrones de Ginebra, el LHC, campeón entre de campeones entre los aceleradores circulares.
Es bueno que pensemos en nuevas formas y que nos arriesguemos a recorrer nuevos caminos, no podemos seguir otro siglo pensando que c, la velocidad del la luz en el vacío, nos tiene contreñidos y nos impedirá para siempre los viajes a otros mundos. Si la forma convencional no nos sirve, hay que buscar otras formas nuevas, otros caminos que nos lleven al otro extremo de la Galaxia y, para que eso sea posible, amigos míos, debemos despojarnos de las ataduras de la física actual que, nos podrá servir de base para avanzar pero, no es suficiente para que se cumpla todo lo que necesitaremos en el futuro.

Fijaos sino, en el empecinamiento que nos traemos desde hace años ya, con “la materia oscura”, con “Bosón de Higgs” y con otros muchos conceptos que desesperados buscamos y no hemos podido encontrar. El mejor ejemplo del objeto perdido es el del Gravitón. ¿Y, si seguimos en nuestras trece y finalmente no aparece ni la “materia oscura ni el bosón de Higgs? ¿qué haremos entonces?
Bueno, entonces sabremos que habíamos elegido caminos equivocados. El camino más cómodo no es siempre el más conveniente y, cuando lanzamos al mundo una teoría que parece que nos da la solución a lo que observamos, debemos, por todos los medios, de contrastarla con la observación y comprobar si son coincidentes teoría y Naturaleza. No siempre lo “más bonito” resulta ser la realidad.
Si somos sensatos y reconocemos que la mecánica cuántica (esa teoría que nos describe a la perfección la Naturaleza), no coincide con nuestro mundo cotidiano que, funciona de otra manera. Entonces, amigos míos, debemos admitir que nuestra realidad está sujeta por nuestras creencias, por nuestros pensamientos y, ¿por qué no? también por nuestros sentimientos. No somos objetivos y dibujamos en nuestras mentes una realidad particular, un escenario del mundo propio, nuestro mundo. Debemos buscar ese otro mundo que escenifica la realidad y acercarnos a él para aprender y saber dónde estamos y a hacia dónde nos dirijimos.

¿Os acordais de aquella noticia?
“Esta semana el equipo de investigación OPERA, del laboratorio europeo de física CERN, dio a conocer una medición realizada en la que se registró por primera vez un exceso de velocidad al límite cósmico que había impuesto la teoría de la relatividad de Einstein. Unos neutrinos, partículas especialmente elusivas, superaron por poco los 299,792.458 kilómetros por segundo a los que viaja la luz, en un recorrido de 730 km a lo largo de la Tierra al laboratorio Gran Sasso. Si bien los físicos advierten que la medición debe de tomarse con cautela, de confirmarse significaría uno de los más profundos sacudimientos hacia los fundamentos con los que se ha construido el edificio de la física moderna —y por lo tanto hacia nuestra realidad.”
La polémica fue grande y, al final, todo se aclaró, se descubrió el error y el Fotón siguió siendo el rey de la velocidad en nuestro Universo. Sin embargo, ¿quién puede negar que existan otros caminos? Si no son los Neutrinos… ¡podríamos ser nosotros! los que, por un medio inesperado, podríamos (no superar pero sí burlar) ir más aprisa que la luz tomando el adecuado camino.

Siempre he dicho que, el Universo es…, casi tan grande como nuestra imaginación. Si eso es cierto, nuestras mentes a pleno rendimiento (al menos alguna) podría iluminarse con la idea de viajar al otro extremo de la Galaxia primero y, al otro extremo del Universo después. ¿Quién sabe hasta dónde podremos llegar? En realidad, ¿Existen límites? NO, creo que no existe ningún límite y, la Naturaleza tiene todas las respuestas para que nosotros, seres pensantes y conscientes, las podamos encontrar.
Pero, como decía al principio, muchas cosas deben cambiar y, la mentalida de hoy, debe dar paso a nuevas formas y nuevas maneras de ver y mirar hacia nuevos horizontes que la Ciencia nos está señalando con insistencia y que no nos atrevemos a visitar.
emilio silvera
Oct
1
La Fisica, ¡que maravilla!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (9)
Comments (9)
En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón puede trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).

Cuando llegamos a los seres unicelulares, se ve que para ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala.
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. Esta fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia entre dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del estado líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este trabajo de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido hacia las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.
Oct
1
Noticias de Marte
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Marte ~
Clasificado en Marte ~
 Comments (0)
Comments (0)
La reproducción de la voz grabada de un directivo de la NASA, que se envió de la Tierra al robot, sonó en el planeta rojo y luego se reenvió de vuelta
Ciencia | 28/08/2012 – 08:50h

Nuevas imágenes de la geografía de Marte enviadas por el Curiosity LVD
Washington. (EFE).- La voz de un ser humano ha surcado hoy por primera vez los cielos desde Marte a la Tierra, y aunque no era una “presencia humana física”, ha supuesto un hito más dentro de la misión del explorador Curiosity, que lleva ya más de 20 días en el planeta rojo. “Hola. Soy Charlie Bolden, Administrador de la NASA, hablando con usted a través de la capacidad de difusión del Curiosity robot, que ahora está en la superficie de Marte”, se escuchó en las instalaciones de la agencia espacial estadounidense (NASA).
“Desde el principio de los tiempos, la curiosidad de la humanidad nos ha llevado a buscar constantemente algo nuevo… Nuevas opciones de vida más allá del horizonte. Quiero felicitar a los hombres y mujeres de nuestra familia de la NASA, así como a nuestros socios comerciales y gubernamentales de todo el mundo por haber dado un paso más en Marte”, continuó la grabación.
Según explicó el mismo Bolden en la cinta, la agencia espera obtener importante información a través del análisis del cráter Gale, que será clave para conocer si Marte fue o será apto para albergar vida. “Curiosity traerá beneficios a la Tierra e inspirará a una nueva generación de científicos y exploradores, mientras se prepara el camino para una misión humana en un futuro no muy lejano “, dijo Bolden en el mensaje grabado acerca de la misión de dos años que llevará a cabo el robot.
La reproducción de la voz grabada de Bolden, que se envió de la Tierra al Curiosity, sonó en el planeta rojo y luego se reenvió de vuelta a la Tierra, se anunció hoy en una rueda de prensa en el Laboratorio Jet Propulsion, en Pasadena, California, junto con nuevas imágenes obtenidas por el explorador con sus diversas cámaras. “Con la presencia de esta voz, se da otro pequeño paso más hacia la presencia humana más allá de la Tierra, y la experiencia de explorar mundos remotos se pone un poco más cerca de todos nosotros”, dijo Dave Lavery, director del programa Curiosity para la NASA.
“A medida que el Curiosity continúe su misión, esperamos que estas palabras sean una inspiración para quien se convierta en el primero en poner un pie sobre la superficie de Marte, y como hizo el gran Neil Armstrong, ponga voz a un paso gigante para la exploración humana”, añadió Lavery al recordar al recién fallecido astronauta

Por otro lado, las imágenes más recientes obtenidas con los teleobjetivos que lleva el robot, muestran una escenas de laderas quebradas y erosionadas, con capas geológicas claramente expuestas, con una resolución y nitidez mucho más elevadas que las anteriores.
Michael Malin, investigador principal del proyecto Mastcam, encargado de procesar y analizar las imágenes que llegan desde Marte, aseguró que esa es una de las zonas donde centrarán sus objetivos. “Algunas de las rocas que se observan son redondeadas, algunas angulares, tienen historias diferentes. Es un sitio geológico muy rico a primera vista y pretendemos pasar por él”, explicó.
En las nuevas fotos del cráter, retocadas por la agencia para contrastar más las diferencias de los estratos, se distingue la grava en primer plano y las dunas al fondo, con zonas de arena de diferentes colores, por lo que tienen distinta composición. Durante la conferencia de prensa, el equipo también informó de los resultados de un ensayo en los Análisis de Muestras del Curiosity en Marte (SAM, siglas en inglés), mediante los que miden la composición de las muestras de la atmósfera, el polvo de roca o el suelo.
La cantidad de aire de la atmósfera terrestre que permaneció tras el lanzamiento en el instrumento que recoge las muestras fue mayor de lo esperado, por lo que comenzaron poniéndolo a prueba con un análisis químico del aire terrestre, antes de que analice los gases presentes en Marte. “Los resultados son una confirmación de la hermosa sensibilidad para la identificación de los gases presentes que tiene SAM”, dijo su investigador principal, Paul Mahaffy.
“Estamos contentos con esta prueba y estamos deseando que llegue la siguiente ejecución en unos pocos días cuando podamos obtener datos de Marte”, añadió. Según informó la NASA, el Curiosity ya está enviando más datos de la superficie de Marte que todos los robots juntos enviados por la agencia con anterioridad. El Curiosity, que aterrizó en la superficie de Marte en la madrugada del pasado 6 de agosto, ha enviado cientos de fotografías en blanco y negro y en color que han proporcionado la vista más nítida de Marte conocida hasta ahora.
Leer más: http://www.lavanguardia.com/ciencia/20120828/54341608681/curiosity-imagenes-voz-marte.html#ixzz2826G8QkQ
Síguenos en: https://twitter.com/@LaVanguardia | http://facebook.com/LaVanguardia
















 Totales: 83.781.474
Totales: 83.781.474 Conectados: 38
Conectados: 38