Nov
15
¡¡Viajar en el Tiempo!!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en ¡Viajar en el Tiempo! ¿Podremos? ~
Clasificado en ¡Viajar en el Tiempo! ¿Podremos? ~
 Comments (13)
Comments (13)

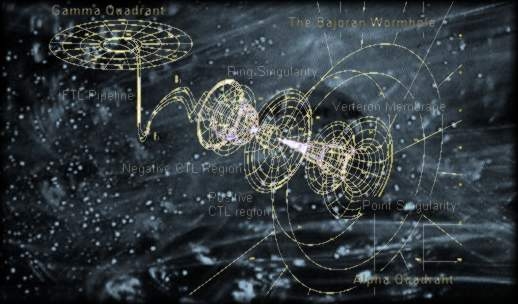



Demostración: Dada la famosa ecuación E=mc². Si c representa la velocidad de la luz, la cual es de aproximadamente 300.000km/seg, para acelerara una masa de tan solo 1kg hasta dicha velocidad se necesitaria una energia de 90000000000000000Newton!! Pero ojo!la masa es masa relativa, no en reposo, y entonces, para la energía total se tiene

donde v es la velocidad del móvil. Si reemplazamos ahora este valor en la ecuación de Einstein se observa entonces que cuando dicha velocidad alcanza la de la luz, el denominador es 0 y por tanto la energía es infinita. Es importante notar que la Ecuación de Einstein expresada así E=mc², donde la masa es masa relativa, no representa la equivalencia masa-energía o energía en reposo, sino la energía total de un cuerpo en movimiento.



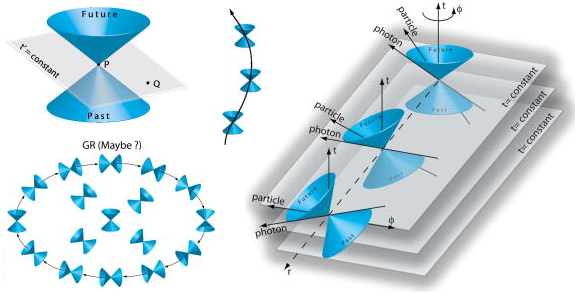
“Otro descubrimiento del siglo XIX que se consideró abstracto e inútil en su tiempo fue la geometría no euclídea. En esta geometría se pueden trazar al menos dos rectas paralelas a una recta dada que pasen por un punto que no pertenece a ésta. Aunque descubierta primero por Gauss, éste tuvo miedo de la controversia que su publicación pudiera causar. Los mismos resultados fueron descubiertos y publicados por separado por el matemático ruso Nikolái Ivánovich Lobachevski y por el húngaro János Bolyai.”“En la geometría encuentro ciertas imperfecciones que considero la razón por la cual esta ciencia, a parte de ser transición a lo analítico, no puede avanzar más allá del estado en que llegó a nosotros desde Euclides. Entre estas imperfecciones encuentro la oscuridad de los conceptos fundamentales de las magnitudes geométricas y de los modos y métodos de representar la medición en estas magnitudes, y con finalmente los vacíos ocasionados en la teoría de las paralelas, cuyos intentos de remiendo por parte de los matemáticos han sido hasta el momento vanos.” Nikolái Ivánovich Lobachevski, The Theory of Parallels,1840.
“Las geometrías no euclídeas fueron estudiadas en su forma más general por Riemann, con su descubrimiento de las múltiples paralelas. En el siglo XX, a partir de los trabajos de Einstein, se le han encontrado también aplicaciones en física.”
Observa la representación gráfica de las siguientes funciones de Riemann:

La superficie de la función (z^2-1)1/4 de Riemann

Superficie de la función (z^4)-1/4 de Riemann.
– Ensayo sobre las Paradojas de la Teoría de Conjuntos.
Y tantos otros antes y después… hicieron posible que llegáramos aquí y, otros que vendrán, harán posible que prosigamos el camino emprendido hace ya mucho tiempo y, no sólo contrinuirán a los posibles viajes en el tiempo (si finalmente fuesen posibles) sino que, además, nos darán las herramientas necesarias para poder llegar al corazón de la materia, de los secrtetos de la Natutaleza y, entonces amigos míos, y sólo entonces, podremos decir que somos auténticos señores del Hiperespacio que llegaremos a dominar para visitar las estrellas lejanas que, al fin y al cabo, ¡es nuestro futuro!
Lo de viajar hacia atrás o hacia adelante en el Tiempo… ¡es otra cosa!
emilio silvera
Nov
15
El Universo y sus enigmas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (12)
Comments (12)
Asombra un poco oir (con más freecuencia de lo que sería deseable) a personas que se consideran inteligentes, decir que ellos saben lo que pasó en los primeros tres minutos a partir de lo que llamamos Big Bang. En realidad, se están refiriendo a que tienen un modelo del Universo temprano, y que este modelo encaja con los resultados que hasta el momento hemos obtenido mediante experimentos y observaciones pero, están apareciendo algunos datos que no dejan bien parado al Big Bang o, por lo menos, lo sitúa en una zona de interrogantes.

Como nadie estuvo allí para captarlo, basados en los datos que hemos podido recopilar, nos imaginamos lo que pudo ser (si es que realmente fue) lo ocurrido en aquellos primeros momentos del Big Bang. Al decir primeros, sitúo ese comenzar a después de la primera fracción de segundo, tiempo en el que, ni las matemáticas nos dejan entrar en él para buscar lo que realmente pasó.
Nov
15
Las misteriosas enanas blancas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Los misterios del Universo ~
Clasificado en Los misterios del Universo ~
 Comments (6)
Comments (6)

Una enana blanca es una pequeña y densa estrella que es el resultado final de la evolución de todas las estrellas (por el ejmplo el Sol), excepto las muy masivas. Según todos los estudios y observaciones, cálculos, midelos de simulación, etc., estas estrellas se forman cuando, al funal de la vida de las estrellas medianas, al final de sus vidas, cuando agotan el combustible de fusión nuclear, se produce el colapso de sus núcleos estelares, y quedan expuestas cuando las partes exteriores de la estrella son expulsadas al espacio interestelar para formar una Nebulosa Planetaria.
El Núcleo se contrae bajo su propia gravedad hasta que, habiendo alcanzado un tamaño similar al de la Tierra , se ha vuelto tan densa (5 x 108 Kg/m3) que sólo evista su propio colapso por la preseión de degeneración de los electrones (como sabeis los electrones son fermiones que estando sometidos al Principio de exclusión de pauli, no pueden ocupar niguno de ellos el mismo lugar de otro al tener el mismo número cuántico y, siendo así, cuando se cjuntan demasiado, se degeneran y comienzan una frenética carrera que, en su intensidad, puede, incluso frenar la implosión de una estrella -como es el caso de las enanas blancas).
Las enanas blancas se forman con muy altas temperaturas superficiales (por encima de los 10 000 K) debido al calor atrapados en ellas, y liberado por combustiones nucleares previas y por la intensa atracción gravitacional que sólo se ve frenada por la degeneración de los electrones que, finalmente, la estabilizan como estrella enana blanca.
Este tipo de estrellas, con el paso del tiempo, se enfrían gradualmente, volviéndose más débiles y rojas. Las enanas blancas pueden constituir el 30 por ciento de las estrellas de la vecindad solar, aunque debido a sus bajas luminosidades de 10-3 – 10-4 veces la del Sol, pasan desapercibidas. La máxima máxima posible de una enana blanca es de 1,44 masas solares, el límite de Shandrasekhar. Un objeto de masa mayor se contraería aún más y se convertiría en una estrella de neutrones o, de tener muha masa, en un agujero negro

Visión artística de una enana blanca, Sirio B – Crédito: NASA, ESA y G. Bacon (STScl)

Una enana blanca comienza a expulsar material y formar una Nebulosa Planetaria
Las enanas blancas son estrellas calientes y pequeñas, generalmente como del tamaño de la Tierra, por lo que su luminosidad es muy baja. Se cree que las enanas blancas son los residuos presentes en el centro de las nebulosas planetarias. Dicho de otra manera, las enanas blancas son el núcleo de las estrellas de baja masa que quedan después de que la envoltura se ha convertido en una nebulosa planetaria.
El núcleo de una enana blanca consiste de material de electrones degenerados. Sin la posibilidad de tener nuevas reacciones nucleares, y probablemente después de haber perdido sus capas externas debido al viento solar y la expulsión de una nebulosa planetaria, la enana blanca se contrae debido a la fuerza de gravedad. La contracción hace que la densidad en el núcleo aumente hasta que se den las condiciones necesarias para tener un material de electrones degenerados. Este material genera presión de degeneración, el cual contrarresta la contracción gravitacional.
Al ser estudiadas más a fondo las propiedades de las enanas blancas se encontró que al aumentar su masa, su disminuye. A partir de esto es que se encuentra que hay un límite superior para la masa de una enana blanca, el cual se encuentra alrededor de 1.4 masas solares (MS). Si la masa es superior a 1.4 MS la presión de degeneración del núcleo no es suficiente para detener la contracción gravitacional. Este se llama el límite de Chandrasekhar.
Debido a la existencia de este límite es que las estrellas de entre 1.4 MS y 11 MS deben perder masa para poder convertirse en enanas blancas. Ya explicamos que dos medios de pérdida de masa son los vientos estelares y la expulsión de nebulosas planetarias.

A esto puede dar lugar la unión de dos enanas blancas
Después de que una estrella se ha convertido en enana blanca, lo más probable es que su destino sea enfriarse y perder brillo. Debido a que las enanas blancas tienen una baja luminosidad, pierden energía lentamente, por lo que pueden permanecer en esta etapa en el orden de años. Una vez que se enfrían, se vuelven rocas que se quedan vagando por el Universo. Este es el triste destino de nuestro Sol.
La detección de enanas blancas es difícil, ya que son objetos con un brillo muy débil. Por otro lado, hay ciertas diferencias en las enanas blancas según su masa. Las enanas blancas menos masivas sólo alcanzan a quemar hidrógeno en helio. Es decir, el núcleo de la estrella nunca se comprime lo suficiente como para alcanzar la temperatura necesaria para quemar helio en carbono. Las enanas blancas más masivas sí llevan a cabo reacciones nucleares de elementos más pesados, es decir, en su núcleo podemos encontrar carbono y oxígeno.
Comparación de tamaños entre la enana blanca IK Pegasi B (centro abajo), su compañera de clase espectral A IK Pegasi A (izquierda) y el Sol (derecha). Esta enana blanca tiene una temperatura en la superficie de 35.500 K.
Allá por el año 1908, siendo Chandraskhar un avanzado estudiante de física, vivía en Madrás, en la Bahía de Bengala (En cuyo Puerto trabajó Ramanujan), y, estando en la aquella ciudad el célebre científico Arnold Sommerfeld, le pidió audiciencia y se pudo entrevistar con él que, le vino a decir que la física que estudiaba estaba pasada, que ahora se estaban estudiando nuevos caminos de la física y, sobre todo, uno a cuya teoría se la llamaba mecánica cuántica que podía explicar el comportamiento de lo muy pequeño.

Chandrasekhar
Cuando se despidieron Sommerfeld dio a Chandrasekhar la prueba de imprenta de un artículo técnico que acaba de escribir. Contenía una derivación de las leyes mecanocuánticas que gobiernan grandes conjuntos de electrones comprimidos en volúmenes pequeños, por ejemplo (para este caso) en una estrella enana blanca.
A partir de aquel artículo, Chandrasekhar buscó más información y estudió estos fenómenos estelares que desembocaban en enanas blancas. Este tipo de estrella habían descuibiertas por las astrónomos a través de sus telescopios. Lo misterioso de las enanas blancas era su densidad extraordinariamente alta de la materia en su interior, una densidad muchísimo mayor que la decualquier otra cosa que los seres humanos hubieran encontrado antes. Chandrasekhar no tenía forma de saberlo cuando abrió un libro de Eddintong que versaba sobre la materia, pero la lucha por desvelar el misterio de e4sta alta densidad le obligaría fibnalmente a él y a Eddintong a afrontar la posibilidad de que las estrellas masivas, cuando mueren, pudieran contraerse para formar agujeros negros.

De las enanas blancas más conocidas y cercanas, tenemos a Sirio B. Sirio A y Sirio B son la sexta y la seéptima estrellas en orden de proxomidad a la Tierra, a 8,6 años-luz de distancia, y Sirio es la estrella más brillante en nuestro cielo. Sirio B orbita en torno a Sirio de la misma manera que lo hace la Tierra alrededor del Sol, pero Sirio B tarde 50 años en completar una órbita a Serio y la Tierra 1 año al Sol.
Eddintong describía como habían estimado los astrónomos, a partir de observaciones con telescopios, la masa y la circunferencia de Sirio B. La masa era de 0,85 veces la masa del Sol; la circunferencia media 118.000 km. Esto significaba que la densidad media de Sirio B era de 61.000 gramos por centímetro cúbico, es decirm 61.000 veces mayor que la densidad del agua. “Este argumento se conoce ya desde hace algunos añis -nos decía Eddintong-” Sin embargo, la mayoría de los astróniomos de aquel tiempo, no se tomaban en serio tal densidad, Sin embargo, si hubieran conocido la vrdad que ahora conocemos: (Una masa de 1,05 soles, una circunferencia de 31.000 km y una densidad de 4 millones de gramos por cm3), la habrían considerado aún más absurda.

Arriba la famosa Nebuliosa planetaria ojo de Gato que, en su centro luce una estrella enana blanca de energéticas radiaciones en el ultravioleta y que, a medida que se vaya enfriando, serán de rayos C y radio hasta que, dentro de unos 100 millones de añosm vieja y fria, será más rojiza y se habrá convertido en eun cadáver estelar.
Aquellos trabajos de Chandraskar y Eddintong desembocaron en un profundo conocimiento de las estrellas de neutrones y, se llego a saber el por qué conseguian el equilibrio que las estabilizaba a través de la salvación que, finalmente encontraban, en la mecánica cuántica, cuando los electrones degenerados por causa del Principio de esclusión de Pauli, no dejaban que la fuerza gravitatoria continuara el proceso de contracción de la estrella y así, quedaba estabilizada como estrella de neutrones.
De la misma manera, se repetía el proceso para estrellas más masivas que, no pudiendo ser frenadas en su implosión gravitatoria por la degeneración de los electrones, sí que podia frenarse la Gravedad, mediante la degeneración de los Neutrones. Cuando esa estrella más masiva se contraía más y más, el Principio de exclusión de pauli que impide que los fermiones estén juntos, comenzaba su trabajo e impedía que los neutrones (que son fermiones), se juntaran más, entonces, como antes los electrones, se degeneraban y comenzaban a moverse con velocidades relativistas y, tan hecho, impedía, por sí mismo que la Gravedad consiguiera comprimir más la masa de la estrella que, de esta manera, quedaba convertida, finalmente, en una Estrella de Neutrones.

Al formarse la estrella de neutrones la estrella se colapsa hasta formar una esfera perfecta con un radio de tan solo unos 10 kilómetros. En este punto la presión neutrónica de Fermi resultante compensa la fuerza gravitatoria y estabiliza la estrella de neutrones. Apenas una cucharilla del material que conforma una estrella de neutrones tendría una masa superior a 5 x 1012 kilogramos.
Los modelos de estrellas de neutrones que se han logrado construir utilizando las leyes físicas presentan varias capas. Las estrella de neutrones presentarían una corteza de hierro muy liso de, aproximadamente, un metro de espesor. Debajo de esta corteza, prácticamente todo el material está compuesto por núcleos y partículas atómicas fuertemente comprimidos formando un “cristal” sólido de materia nucleica.
Son objetos extremadamente pequeños u densos que surgen cuando estrellas masivas sufren una explosión supernova del tipo II, el núculeo se colapsa bajo su propia gravedad y puede llegar hasta una densidad de 1017 Kg/m3. Los electrones y los protones que están muy juntos se fusionan y forman neutrones. El resultado final consiste solo en neutrones, cuyo material, conforma la estrella del mismo nombre. Con una masa poco mayor que la del Sol, tendría un diámetro de sólo 30 Km, y una densidad mucho mayor que la que habría en un terón de azúcar con una masa igual a la de toda la humkanidad. Cuanto mayor es la masa de una estrella de neutrones, menor será su diámetro. Está compuesta por un interior de neutrones superfluidos (es decir, neutrones que se comportan como un fluido de viscosidad cero), rodeado por más o menos una corteza sólida de 1 km de grosos compuesta de elementos como el hierro. Los púlsares son estrellas de neutrones magnetizadas en rotación. Las binarias de rayos X masivas tambioén se piensan que contienen estrellas de neutrones.
Todos aquellos argumentos sobre el comportamiento de las enanas blancas vinieron a desembocar en la paradoja de Edddintong que, en realidad, fue resulta por el Joven Chandrasekhar en el año 1925 al leer un artículo de R.H. Fowler “Sobre la materia densa”. La solución residía en el fallo de las leyes de la física que utilizaba Eddintong. Dcihas leyes debían ser reemplazadas por la nueva mecánica cuántica, que describía la presión en el interior de Sirio B y otras enenas blancas como debida no al calor sino a un fenómeno mecanocuántico nuevo: los movimientos degenerados de los electrones, también llamado degeneración electrónica.
La degeneración electrónica es algo muy parecido a la claustrofia humana. Cuando la materia es comprimida hasta hasta una densidad 10.000 veces mayor que la de una roca, la nube de electrones en torno a cada uno de sus núcleos atómicos se hace 10.000 veces más condensada, Así, cada electrón queda confinado en una “celda” con un volumen 10.000 veces menor que el volumen en el que previamente podía moverse. Con tan poco espacio disponible, el electrón, como nos pasaría a cualquiera de nosotros, se siente incómodo, siente claustrofobia y comienza a agitarse de manera incontrolada, golpeando con enorme fuerza las paredes de las celdas adyacentes. Nada puede deternerlo, el electrón está obligado a ello por las leyes de la mecánica cuántica. Esto está producido por el Primncipio de esclusión de Pauli que impide que dos fermiones estén juntos, así que, esta fuerza es, la que finalmente posibilita que la estrella que se comprime más y más, quede finalmente, constiruida estable como una enana blanca.
emilio silvera
















 Totales: 75.427.629
Totales: 75.427.629 Conectados: 83
Conectados: 83























