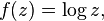Es cierto lo que decía el profesor venezolano Alberto R. Mejías: “A pesar de carecer actualmente de formulación dinámica, es posible obtener gran cantidad de información sobre Teoría M, teoría que se postula como unificadora de todas las interacciones, a partir de sus sectores perturbacionales y de baja energía. En las regiones perturbacionales adecuadas, la Teoría M adopta la apariencia de la Teoría de Cuerdas. Al considerar su límite de baja energía, surge la supergravedad en once dimensiones. Aquí se indica cómo Teoría M puede ser considerada como una deformación biparamétrica de Geometría Clásica, dónde un parámetro controla la generalización de puntos a lazos y el otro parámetro controla la suma sobre topologías de superficies RIEMANN. La formulación matemática final de Teoría M tendrá que considerar Teoría de Fibrados Vectoriales, Teoría K y Geometría No Conmutativa.

Y es cierto que, actualmente, la Teoría M nos conduce de manera directa hasta el objeto matemático más complejo y más rico que jamás se ha tocado en Física. Finalmente, nos lleva a la unificación de todas las grandes teorías anteriores y consigue, de manera natural, unificar la relatividad general de Einstein con la cuántica de Planck. Es decir, allí, en la Toería M, se describen juntas las cuatro fuerzas de la Naturaleza. Lo curioso del caso es que, cuando se desarrollan las ecuaciones de esta compleja teoría, aparezcan las ecuaciones de Einstein de la Relatividad General que, subyacen dentro de ella.

Lo cierto es que, si miramos hacia atrás en el tiempo, nos encontramos con el hecho cierto de que, Einstein pudo formular su bella teoría de la relatividad general gracias a una conferencia que dio Riemann y que, habiendo pedido ayuda a su amigo Marcel Grosmman, éste le mandara una copia en la que, aparecía el Tensor Métrico de Riemann que le dio a Einstein las herramientas de las que carecía.

Aquel trabajo de Riemann, su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

De todo aquello y buscando nuevos caminos para poder responder a preguntas planteadas que nadie había sabido contestar, surgieron teorías que, como la de Kaluza-Klein, nos trajeron hasta la supersimetría, supergravedad y a todas lasversiones de la teoría de cuerdas que Witten ha unificado en la Teoría M. Pensar en las complejas matemáticas topológicas requeridas por la teoría de supercuerdas puede producir incomodidad en muchas personas que, aún siendo físicos, no están tan capacitados para entender tan profundas ideas.

Bernhard Riemann introdujo muchas nuevas ideas y fue uno de los más grandes matemáticos. En su corta vida (1.826 – 1.866) propuso innumerables propuestas matemáticas que cambiaron profundamente el curso del pensamiento de los números en el planeta Tierra, como el que subyace en la teoría relativista en su versión general de la gravedad, entre otras muchas (superficie de Riemann, etc.). Riemann les enseñó a todos a considerar las cosas de un modo diferente.

• Numerosos ejemplos de superficies de Riemann no compactas se obtienen por el procedimiento de extensión analítica.

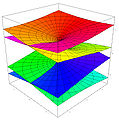
La superficie de Riemann asociada a la función holomorfa “tiene su propia opinión” y decide por sí misma cuál debería ser el, o mejor, su dominio, con independencia de la región del plano complejo que nosotros podamos haberle asignado inicialmente.

Podríamos encontrar otros muchos tipos de superficies de Riemann.

Este bello concepto desempeña un papel importante en algunos de los intentos modernos de encontrar una nueva base para la física matemática (muy especialmente en la teoría de cuerdas), y al final, seguramente descubrirá el mensaje que encierra.

El caso de las superficies de Riemann es fascinante, aunque desgraciadamente sólo es para iniciados. Proporcionaron los primeros ejemplos de la noción general de variedad, que es un espacio que puede pensarse “curvado” de diversas maneras, pero que localmente (por ejemplo, en un entorno pequeño de cualquiera de sus puntos), parece un fragmento de espacio euclídeo ordinario.

La esfera de Riemann juega un papel fundamental en cualquier sistema cuántico de dos estados, describiendo el conjunto de estados cuánticos posibles. Para una partícula de espín 1/2, su papel geométrico es particularmente evidente puesto que los puntos de la esfera corresponden a las posibles direcciones espaciales para el eje de giro. En otras situaciones el papel de la esfera de posibilidades de Riemann está bastante más oculto, con una relación mucho menos clara con la geometría espacial.

Si estudiamos de manera profunda lo que Riemann nos legó, tendremos que convenir en el hecho irrefutable de que fue, junto con otros grandes matemáticos, uno de los que posibilitaron que la humanidad siguiera avanzando en el conmocimiento de la Naturaleza. La esfera de Riemann, superficie de Riemann compacta, el teorema de la aplicación de Riemann, las superficies de Riemann y aplicaciones complejas… Todo de una enorme importancia para las matemáticas en general y la geometría en particular… y, para la física también.

                                                            Ernst Mach

Einstein supo captar algunas buenas ideas sueltas que aunó en un sólo conjunto para convertirlas en teoría unificada de todas ellas que sueltas no decían tanto como juntas y bien colocadas. Así, hizo suyos los conceptos de Mach, Lorentz, Maxwell e incluso Galileo y finalmente Riemann -entre otros- para dejar sentadas las bases de cómo era la Naturaleza mediante las dos versiones de la teoría relativista, la especial y la general.

“La inercia de cualquier sistema es el resultado de su interacción con el resto del Universo. En otras palabras, cada partícula del universo ejerce una influencia sobre todas las demás partículas.”

Este concepto le hizo pensar profundamente y le llevó a todas sus ideas de la relatividad general que pudo exponer gracias a Riemann. Sin la geometría de Riemann de los espacios curvos, sin su tensor métrico…

En escritos anteriores consideramos dos aspectos de la relatividad general de Einstein, a saber, el principio de la relatividad, que nos dice que las leyes de la física son ciegas a la distinción entre reposo y movimiento uniforme; y el principio de equivalencia, que nos dice de qué forma sutil deben modificarse estas ideas para englobar el campo gravitatorio.

Ahora hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco. Él no tenía forma alguna de anticipar la extraordinaria velocidad de la luz.

Parece que tanto Galileo como Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida.

Pero la comprensión adecuada de estas ideas tuvo que esperar hasta el siglo XX, cuando se reveló la verdadera naturaleza de las fuerzas químicas y de las fuerzas que mantienen unidos los átomos individuales. Ahora sabemos que tales fuerzas tienen un origen fundamentalmente electromagnético (que vincula y concierne a la implicación del campo electromagnético con partículas cargadas) y que la teoría del electromagnetismo es también la teoría de la luz.

Para entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría que Einstein también aprovechó para la suya.

Esta teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que un unidades ordinarias es aproximadamente 3 × 10⁸ metros por segundo.

Sin embargo, esto nos presenta un enigma si queremos conservar el principio de relatividad. El sentido común nos diría que si se mide que la velocidad de la luz toma el valor concreto c en el sistema de referencia del observador, entonces un segundo observador que se mueva a una velocidad muy alta con respecto al primero medirá que la luz viaja a una velocidad diferente, aumentada o disminuida, según sea el movimiento del segundo observador.

Pero el principio de relatividad exigiría que las leyes físicas del segundo observador (que definen en particular la velocidad de la luz que percibe el segundo observador) deberían ser idénticas a las del primer observador. Esta aparente contradicción entre la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede hacerse compatible con la constancia de una velocidad finita de la luz.

La velocidad de la luz en el vacío es la misma para todos los observadores inerciales, independientemente del estado de movimiento de la fuente de luz, c siempre irá a la velocidad de 299.792.458 metros por segundo.

En el caso de un espacio tiempo bidimensional (x,t) representamos el cono de luz como dos líneas cruzadas, una de pendiente 1 y otra de pendiente -1.(Estamos normalizando la velocidad de la luz al valor c=1).

¿Cómo funciona esto? Sería normal que cualquier persona creyera en la existencia de un conflicto irresoluble entre los requisitos de una teoría como la de Maxwell, en la que existe una velocidad absoluta de la luz, y un principio de relatividad según el cual las leyes físicas parecen las mismas con independencia de la velocidad del sistema de referencia utilizado para su descripción.

¿No podría hacerse que el sistema de referencia se moviera con una velocidad que se acercara o incluso superara a la de la luz? Y según este sistema, ¿no es cierto que la velocidad aparente de la luz no podría seguir siendo la misma que era antes? Esta indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.

Pero semejante imagen de la naturaleza de la luz había entrado en conflicto con la observación a lo largo de los años, como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.

En la teoría de Maxwell, la luz toma forma de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.

El punto de vista geométrico-espaciotemporal nos proporciona una ruta particularmente clara hacia la solución de la paradoja que presenta el conflicto entre la teoría de Maxwell y el principio de relatividad.

Este punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento, ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir familias de todos los diferentes rayos de luz que pasan a ser familias de líneas de universo, etc.

Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.

En alguna ocasión (como contrapunto) he puesto el ejemplo del principio de relatividad contrario a lo que acabo de explicar: el niño que viaja con su padre en un tren que marcha a la velocidad de 80 Km/h. Ambos están asomados por la ventanilla del tren. El niño, en el momento de pasar junto a la estación (en la que el jefe de estación parado en el andén, observa el paso del tren), arroja una pelota por la ventanilla que sale disparada de su mano, en la misma dirección de la marcha del tren, a 20 Km/h. Ahora, tanto el padre del niño como el jefe de estación, tienen un aparato que mide la velocidad de la pelota. El resultado es dispar: el jefe de estación ve que su aparato estima la velocidad de la pelota en 100 Km/h, mientras que el padre del niño la sitúa en 20 km/h. La explicación es sencilla. El aparato del jefe de estación, parado e inmóvil al medir la velocidad de la pelota obtiene el resultado de la suma de la velocidad del tren (80 Km/h) y de la velocidad de impulso del lanzamiento (20 Km/h), pero el padre del niño, montado en el tren que marcha a 80 Km/h, está en movimiento, y su aparato también, con lo cual sólo puede medir la velocidad de lanzamiento (20 Km/h). Así que las dos mediciones del mismo fenómeno nos ha dado un resultado muy diferente, todo vez que depende del observador y de que esté en reposo o en movimiento.

¡Dichoso niño! Nos ha demostrado que, en ciertas situaciones…sí importa el movimiento

Sin embargo, la velocidad de la luz es invariante, y si pudiéramos suponer que el niño lanzaba un rayo de luz en lugar de una pelota, tanto el jefe de estación como el padre del niño habrían medido la misma velocidad. La luz corre siempre lo mismo, independientemente de que su fuente esté parada o en movimiento, o de que el observador que la  mida esté en reposo o en movimiento. Sin embargo, el fenómeno de ralentización del tiempo, cuando se viaja a velocidades relativistas, es otra historia.

La imagen espaciotemporal fue introducida por primera vez por Hermann Minkowski (1.864 – 1.909), que era un matemático extraordinariamente bueno y original. Casualmente él fue también uno de los profesores de Einstein en el ETH, Instituto Federal de Tecnología de Zurich, a finales de la última década del siglo XIX.

De hecho, la idea misma del espacio-tiempo es de Minkowski,  que habiendo leído la teoría de la relatividad especial de su antiguo alumno,  en 1.908 escribía:

“En lo sucesivo, el espacio por sí solo y el tiempo por sí solo están condenados a desvanecerse en meras sombras, y sólo un tipo de unión entre ambos conservará una realidad independiente“.

Se deduce de estas palabras que Minkowski, cuando conoció la teoría de la relatividad de Einstein sacó sus propias consecuencias, y a pesar de las maravillosas intuiciones físicas de su alumno y de las excelentes contribuciones de Lorentz y Poincaré, fue él, Minkowski, el que aportó un punto de vista fundamental y revolucionario, el espacio-tiempo, la geometría subyacente en la teoría de la relatividad especial.

           Hermann Minkowski

Sumergirse en este tema, sin que nos demos cuenta, nos puede llevar a plantearnos complejos tales como que la geometría de Minkowski tiene grupos de simetría tan grandes como el que tiene el espacio-tiempo G de la física galileana, y no sólo están todos los puntos M (Minkowski) en pie de igualdad, sino que todas las velocidades posibles (direcciones de género tiempo que apuntan al futuro) están también en pie de igualdad entre sí.

Para evitar meterme en un callejón sin salida (para mí), dejaré aquí el giro que está tomando el trabajo que, sin que pueda impedirlo, y como si tuviera vida propia, profundiza y se hace más complejo hasta sobrepasar mis limitados conocimientos. De todas las maneras, tendremos que convenir en el hecho cierto de que, en Física, han pasado cosas que te cortan la respiración, como por ejempo:

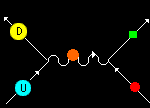
La ecuación de Dirac de ondas relativista de la mecánica cuántica fue formulada por Paul Dirac en 1928. Da una descripción de las partículas elementales de espín ½, como el electrón, y es completamente consistente con los principios de la mecánica cuántica y de la teoría de la relatividad especial. Además de dar cuenta del espín, la ecuación predice la existencia de antipartículas

La ecuación de Dirac para el electrón supuso un momento crucial para la física en muchos aspectos. En 1.928, cuando Dirac propuso su ecuación, las únicas partículas conocidas para la ciencia eran los electrones, los protones y los fotones. Las ecuaciones de Maxwell libres describen el fotón (como fue previsto por Einstein en 1.905) en un primer trabajo cuyas ideas fueron desarrolladas por Einstein, Bose y otros, hasta que en 1.927 Jordan y Pauli proporcionaron un esquema matemático global para describir los fotones libres de acuerdo con la teoría de Maxwell para el campo libre cuantizado.

Además, tanto el protón como el electrón, parecían estar muy bien descritos por las ecuaciones de Dirac. La interacción electromagnética, que describe la influencia de los fotones sobre los electrones y los protones, estaba excepcionalmente tratada mediante la receta de Dirac, a saber, mediante la idea gauge (tal como fue introducida básicamente por Weyl en 1.918), y el propio Dirac ya había empezado a construir el 1.927 una formulación de una teoría completa de los electrones (o protones) en interacción con protones.

Así pues, todas las herramientas básicas parecían estar más o menos a punto para la descripción de todas las partículas conocidas de la naturaleza, junto con sus más destacadas interacciones.

Los físicos de la época no eran tan ilusos como para pensar que todo aquello les pudiera llevar pronto a una “teoría del todo”. Eran conscientes de que, ni las fuerzas necesarias para mantener unidos los núcleos (las que ahora llamamos nuclear fuerte) ni los mecanismos responsables de la desintegración radiactiva (ahora fuerza nuclear débil) podrían acomodarse sin importantes avances adicionales.

Allí algo no estaba bien, ya que si los electrones y los protones estilo Dirac, que sólo interaccionaban electromagnéticamente, fueran los únicos ingredientes de los átomos, incluyendo sus núcleos, entonces todos los núcleos ordinarios (excepto el simple protón que constituye el núcleo de hidrógeno) se desintegrarían al instante debido a la repulsión electrostática de las cargas positivas predominantes.

¡Tenía que estar actuando alguna otra cosa desconocida, algo que explicara una fuerte influencia atractiva dentro del núcleo! En 1.932, Chadwick descubrió el neutrón, y se comprendió por fin que el modelo protón/electrón para el núcleo, que había sido popular hasta entonces, debía ser reemplazado por otro en el que los protones y los neutrones estarían presentes, y donde una fuerte interacción protón-neutrón mantendría el núcleo unido.

Pero esta fuerza fuerte no era lo único que faltaba en el conocimiento de la época.

La radiactividad del uranio se conocía desde las observaciones de Henri Becquerel en 1.896, y se presentaba como el resultado de otra interacción (la fuerza débil) diferente de la fuerte y de la electromagnética. Incluso un neutrón, si se deja libre, sufriría una desintegración radiactiva en un periodo de unos quince minutos.

Uno de los misteriosos productos de la radiactividad era el evasivo neutrino, propuesto como hipótesis provisional por Pauli en 1.929, aunque no fue obserado directamente hasta 1.956.

Ahora, las cosas se conocen mejor y se dispone de una imagen más completa conocida como modelo estándar de la física de partículas. Este modelo parece acoger casi todo el comportamiento observado concerniente al vasto conjunto de partículas que hoy conocemos. Al fotón, el electrón, el protón, el positrón y el neutrón, se han añadido el muón y los diversos neutrinos, los piones (predichos por Yukawa en 1.934), los kaones, los lambdas, los sigmas y la celebradamente predicha por Gell-Mann, la omega menos.

El antiprotón fue directamente observado en 1.955, y el antineutrón en 1.956. hay nuevos tipos de entidades conocidas como los quarks, gluones, bosones W⁺, W^– y Z⁰; hay vastas hordas de partículas cuya existencia es tan fugaz que no han sido nunca directamente observadas, por lo que suelen llamar “resonancias”.

El formalismo de la teoría moderna exige así mismo entidades transitorias llamadas partículas “virtuales”, y también cantidades conocidas como “fantasmas” que están aún más lejos de poder ser observadas en directo. Existe un número desmesurado de partículas propuestas (aún no observadas) que son predichas por ciertos modelos teóricos, aunque no son en absoluto consecuencias del andamiaje general de la física de partículas aceptada: a saber, bosones X, axiones, fotinos, gluinos, monopolos magnéticos, dilatones, etc.

Está también la misteriosa partícula de Higgs (aún no observada) cuya existencia, de una u otra forma, es esencial para la física de partículas actual, donde la partícula de Higgs se considera responsable de la masa de todas las partículas.

Bueno, no creo que el gravitón sea tan feo, y, además, algo sí sabemos de él, es un bosón de espín par,  ya que está asociado a un campo clásico tensorial de segundo orden. En cuanto a la masa del gravitón las mediciones experimentales dan una cota superior del orden de m_g = 1,6 × 10⁻⁶⁹ kg, aunque podría ser exactamente cero. Lo cierto es que está siendo muy esquiva ésta partícula a la hora de dejarse pillar. Se cree que es la partícula mediadora de la fuerza gravitatoria y, aunque no está inmersa en el Modelo estándar, sí está descrita por la teoría de Einstein de la Gravedad.

Es bien sabido que la mecánica cuántica (el universo de las partículas subatómicas) y la relatividad general (el universo de los grandes objetos cosmológicos), de momento no han sido unidas; se rechazan mutuamente con una ferocidad asombrosa.

Parece que la teoría de cuerdas no sólo no rechaza estas dos teorías antagónicas, sino que en sus más altas dimensiones las acoge de manera natural, y ambas se complementan para formar un todo en el que tienen cabida el universo de las partículas, de la gravedad, de las fuerzas fundamentales y de la materia.

Es bonito pensar que un día, pasado el tiempo, se contará con ese modelo completo que, sin estridencias, dé cabida a todo y nos lo pueda explicar todo. Un sueño que cada día está más cerca y, si nadie lo remedia y nuestra imaginación sigue funcionando como hasta el momento lo ha venido haciendo… ¡Grandes cosas se verán!

Si hemos sido capaces de vaticinar la existencia del positrón (la antimateria), el neutrino que explica la masa “perdida”, la existencia de agujeros negros, o, llegar hasta el mismo corazón de la materia ¡los átomos! ¿De qué no seremos capaces?

Pero, a todo ésto debenmos aprender con la Ciencia a…dudar de los “expoertos” (como nos recomensaba Feynman).

emilio silvera

[?]

La técnica de la interferometría de muy larga base a longitudes de onda milimétricas (mm-VLBI) ha permitido obtener imágenes de los motores centrales de las galaxias activas con una resolución angular de decenas de microsegundos de arco. Para aquellos objetos más cercanos (M87, SgrA) se obtienen resoluciones lineales del orden de las decenas de Radios de Schwarzschild, lo que permite estudiar con detalle único la vecindad de los agujeros negros  supermasivos.

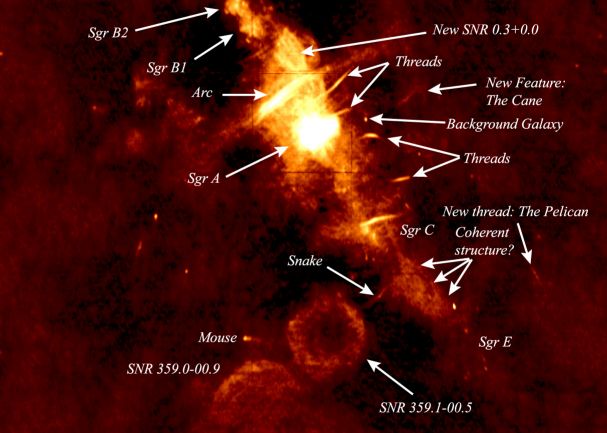
Al sintonizar hacia el centro de la Vía Láctea, los radioastrónomos exploran un lugar complejo y misterioso donde está SgrA que…¡Esconde un Agujero Nefro descomunal! Las observaciones astronómicas utilizando la técnica de Interferometría de muy larga base, a longitudes de onda milimétricas proporcionan una resolución angular única en Astronomía. De este modo, observando a 86 GHz se consigue una resolución angular del orden de 40 microsegundos de arco, lo que supone una resolución lineal de 1 año-luz para una fuente con un corrimiento al rojo z = 1, de 10 días-luz para una fuente con un corrimiento al rojo de z = 0,01 y de 10 minutos-luz (1 Unidad Astronómica) para una fuente situada a una distancia de 8 Kpc (1 parcec = 3,26 años-luz), la distancia de nuestro centro galáctico. Debemos resaltar que con la técnica de mm-VLBI disfrutamos de una doble ventaja: por un lado alcanzamos una resolución de decenas de microsegundos de arco, proporcionando imágenes muy detalladas de las regiones emisoras y, por otro, podemos estudiar aquellas regiones que son parcialmente opacas a longitudes de onda más larga.

Las galaxias activas tienen nucleos que brillan tanto, que pueden llegar a ser más luminosos que las galaxias que los alberga. Estas galaxias activas sae caracterizan porque en sus núcleos ocurren procesos no-térmicos que liberan enormes cantidades de energía que parece provenir de una región muy pequeña y brillante situada en el corazón de la galaxia.

Son muchos los indicios que favorecen la hipótesis de que tales objetos son agujeros negros muy masivos (del orden de 100-1000 millones de veces la masa del Sol), con un tamaño de 1 minuto-luz o varios días-luz. La enorme fuerza gravitatoria que ejercen estos agujeros negros atrae el gas y las estrellas de las inmediaciones, formando el denominado disco de acrecimiento que está en rotación diferencial en torno al objeto masivo.

El modelo de “Agujero Negro + disco de acrecimiento” es el más satisfactorio hoy día para explicar las propiedades de los núcleos activos de galaxias. Un aspecto muy destacado en la morfología de las regiones compactas de los núcleos activos es la presencia de una intensa emisión radio en forma de chorros (los denominados Jets relativistas), que están formados por un plasma de partículas relativistas que emanan del núcleo central y viajan hasta distancias de varios megaparsec.

[?]

Algunas veces, cuando nos adentramos en teorías muy avanzadas de la Física que pretende “desnudar” al Universo para conocerlo en su más absoluta desnudez, uno no puede dejar de generar la idea de que, estamos volviendo de nuevo a escenarios mitológicos en los que, la imaginaciónn del hombre dibujaba escenarios que ahora nos pueden parecer demenciales, y, sin embargo, acercarse a ésta nueva Teoria que llaman de supercuerdas… No estámucho más alejado de todo aquello guardando las distancias entre ambas imaginaciones.

Esta “nueva teoría” la de Supercuerdas, nos dice que el Universo consta de diez dimensiones de espacio y una de tiempo que están creadas por delgadas cuerdas que, al mismo modo que si se trataran de las cuerdas de una lira, pueden vibrar, y, al vibrar, van creando partículas con las resonancias o notas que se generan de sus vibraciones.

En la Mitología muchos dioses tocan instrumentos musicales formados por cuerdas que al ser rasgadas suavemente van generando melódicos sonidos y, las diosas tejedoras van hilando el destino del mundo. La lira de Apolo o el Arpa de Orfeo se me vienen a la mente recordando escenas que la mitología nos dejó.

Claro que, llegó Tales de Mileto el antiguos  filósofo griego que nació en Mileto en la Jonia griega. Él fue, la fuente principal para la filosofía y la ciencia. Identificado como la primera persona que investigó los principios básicos, la cuestión de las sustancias procedentes de la materia y, por tanto, como el fundador de la escuela de filosofía natural. Thales estaba interesado en casi todo, la investigación de casi todas las áreas del conocimiento, la filosofía, la historia, la ciencia, las matemáticas, la ingeniería, la geografía y la política.

Propuso teorías para explicar muchos de los eventos de la naturaleza, la sustancia primordial, la importancia que tenía el agua para la vida, el apoyo de la tierra, y las causas de los cambios. Thales estaba muy involucrado en los problemas de la astronomía y formuló una serie de explicaciones de los acontecimientos cosmológicos en los que, (se decía) que tradicionalmente participan entidades sobrenaturales.

Su enfoque cuestionador a la comprensión de los fenómenos celestes fue el comienzo de la astronomía griega. Las hipótesis de Thales eran nuevas y audaces, el fue el que liberó a los fenómenos naturales de la intervención divina, el que allanó el camino hacia la empresa científica. Fundó la escuela de Mileto de la filosofía natural, desarrolló el método científico que más tarde y pasado el tiempo iniciaó la iluminación occidental en el campo científico. Una serie de anécdotas está estrechamente relacionada con las investigaciones de Thales sobre el Cosmos. Tales fue muy apreciado en la antigüedad, y una carta citada por Diógenes Laercio, y que pretendía ser de Anaxímenes a Pitágoras, informó “…que todo nuestro discurso debe comenzar con una referencia a Thales.” Fue el primero que dejó la mitología para emplear la lógica.

Claro que el relato sobre Mileto, aunque irremediablemente relacionado con el presente, es cosa del pasado. Ahora, como entonces, nos seguimos haciendo las mismas preguntas de ¿dónde estamos?, ¿qué hacemos aquí? ¿qué es la materia? y ¿de qué manera se rige el Universo en realidad? Estas y mil preguntas más son las que nuestra curiosidad nos hace formular con la esperanza de que alguien… nos pueda ofrecer alguna respuesta.

La Física del último siglo ha sido asombrosa y los avances a la vista están. Hemos llegado con la Mecánica Cuántica y la Relatividad hasta un Universo dosdoblado en dos partes: Uno que nos cuenta como es el microcosmos, ese “mundo de lo muy pequeño” y, el otro, nos habla de lo macroscópico, lo muy grande. Partículas infinitesimales y supercúmulos de galaxias conforman nuestro saber del Cosmos y, queriendo desentrañar los secretos que nos esconde, imaginamos teorías que pretenden ir encaminadas a desvelarlos.

         Aquí, en la figura, dicen que hay 7 dimensiones

Y, mientras tanto buscamos y procuramos indagar en lo más profundo de la Naturaleza, por el camino, podemos encontrarnos con gente que dicen cosas: “Detectan huellas de otras siete dimensiones en nuestro Universo Un mapa alternativo de la energía cósmica en el big bang corroboraría la teoría de las supercuerdas.” Es entonces cuando uno, no sabe si reir o llorar, al ver la osadía que algunos tienen que, por buscar un poco de notoriedad y algunos minutos de “gloria”, no se recatan en decir sandeces que no tienen ninguna base científica. Pero, los medios de comunicación ¡lo soportan todo!

Quiero recordar que lfue la Revista Time la que vino a poner la guinda en el léxico de la Física de partículas al proclamar la teoría de las Supercuerdas a bombo y platillo, lanzando a los cuatro vientos la noticia de una Teoria de Tdo. Una teoría que proponía una descripción unificada de todas las fuerzas de la Naturaleza, hasta la Gravedad, tan díscola ella negándose a entrar en el Modelo Estándar de la Física de Partículas, estaría allí incluída y cómodamente instalada en una Teoría libre de parámetros aleatorios e infinitos. ¡Qué maravilla!

La premisa básica de la nueva teoría era que reemplazaba a las familiares partículas puntuales por otras que eran segmentos cortos “de cuerda”. La teoría de cuerdas se caracteriza por una estructura que empuja las fronteras de las matemáticas (como la física ya ha hecho en alguna otra ocasión en el pasado) y las limitaciones conceptuales de la imaginación humana hasta extremos antes nunca experimentados.

Como todo en este mundo, la creación de esta teoría tiene su propia historia y sus propios héroes: Gabrielle Veneziano, Johon Schwartz, André Neveu, Pierre Ramond, Jeff Harvey, Joel Sherk, Michael Green, David Gross y un  dotado flutista de Hamelin que responde al nombre de Edward Witten y cuya flauta, etá hecha de increibles ecuaciones de tal complijidad topológica que, hasta a los más afamados físicos, se les ponen de punta los pelos de las cejas al enfrentarse a ellas.

Hablamos y hablamos de un universo hecho con  dimensiones extra que, pueden ser 10, 11 o 26 y, lo curioso del caso es que, aparte de una temporal que está presente en todas esas variantes, con el resto siempre hacemos el mismo reparto: tres de espacio (que es en el que nos movemos y no podemos renegar de su existencia) y, el resto -no importa el número- son dimensiones compactadas en el límite de Planck, al que, naturalemte, no tenemos manera de llegar.

Los tiempos cambian, y, con los cambios llegan las nuevas doctrinas o creencias, y, ¿por qué no? nuevas teorías. Desde hace algún tiempo venimos dando vueltas y vueltas, en el campo de la Física, a estas avanzadas teorías que no podemos demostrar, toda vez que, al contrario del Modelo Estándar, no son -por ahora- verificables sus predicciones. Me estoy refiriendo, como habeis podido suponer a la Teoría de supercuerdas, La cuerdad Heterótica, la Supergravedad y Supersimetría, y, finalmente, la última versión que viene a ser un compendio de todas las demás, la Teoría M.

Como nos dice Brian Greene en uno de los capítulos del libro El tejido del cosmos, que él titula: “Especulaciones sobre el espacio y el tiempo en la teoría M”, hoy, tres décadas después de la articulación de la teoría de cuerdas,la mayoría de los que trabajan en ella, creen que aún no tenemos una respuesta general para la pregunta fundamental: ¿qué es la teoría de cuerdas? A pesar de que sabemos bastante de la teoría, sus características más elementales son familiares y, a estas alturas, casi cercanas. Tampoco debemos despreciar los éxitos que ha cosechado y, desde luego, es bien sabido todo lo que nos promete y también ¿cómo no? los desafíos que suponen lograr todas esas promesas que en ella están encerradas.

La relatividad especial tiene la constancia de la Velocidad de la luz, la relatividad general tiene el principio de Equivalencia, la mecánica cuántica tiene, el principio de Incertidumbre y, sin embargo, los teóricos de cuerdas aún siguen buscando algo de lo que carece la teoría de cuerdas que, precisamente es: el tipo de principio nuclear que se encontraron en aquellas otras teorías y le dan razón de ser y la sólida base que toda teoría necesita para ser…¡una auténtica teoría!

Esa nueva teorías quiere explicarlo todo. Nada puede estar fuera de ella: ¡El Universo que  es, todo lo que existe, ahí estará!

La Teoría de Cuerdas nos habla de un lugar muy distante, casi tan distante como Hoz o la Atlántida (no, no sonrías Kike, que hablo en serio). Esta Teoría nos quiere llevar hasta los dominios de Planck, un lugar que nadie ha visitado nunca. Ni con un LHC que tuviera un millón de veces la potencia de energía del que ahora busca el Bosón de Higgs, podríamos ir allí. Tan lejano está ese lugar que, cuando los científicos tratan de llegar a él, situado en los primeros instantes después del comienzo del Tiempo, no saben, las matemáticas no responden a sus planteamientos y, de esa manera, nunca hemos podido llegar a saber que sucedió en aquellas primeras fracciones de segundo en el nacimiento del Big Bang, donde, supuestamente, se encuentra el límite de Planck.

¿Será tan difícil encontrar las “cuerdas” como localizar el mundo perdido de la Atlántida? Bueno, por aquí cerca de mi casa, en las costas de Doñana, en el mismo epicentro del Golfo de Cádiz, un equipo de científicos están buscando, afanosamente esa Ciudad perdida que nadie sabe si es leyenda o fue realidad alguna vez. Queda un atisbo de esperanza de poder encontrarla. Algunos textos antiguos la mencionan. Sin embargo, de las cuerdas ¿qué tenemos? ¡La Imaginación de algunos! ¡Las esperanzas de muchos!

Ni observando con una lupa podremos descubrir más de tres dimensiones de espacio en nuestro mundo cotidiano, la otra que completa el cuadro en el que estamos inmersos, según Einstein, es el Tiempo que siempre nos acompaña. Hasta ahí todo está -más o menos- conforme. Sin emnbargo, cuando se nos habla de 11 dimensiones de las que quitamos las cuatro antes mencionada y nos quedan siete compactadas o enrolladas…pero,  enrollada ¿dónde y cómo? Bueno, la teoría arranca de la Gravedad, que se basa en la geometría, así que cabe visualizar que algunas de esas dimensiones estén enrolladas en una bola minúscula. El tamaño de la bola es el característico del régimen de Planck, 10^-33 centímetrtos que viene a ser el tamaño de la cuerda que reemplaza a la partícula puntual.

Así, las partículas que conocemos, surgen en la forma de vibraciones de esas cuerdas, es decir, sus resonancias producen las partículas y, esas cuerdas tensadas, tendrían un número infinito de modos vibración (ese es, el fundamento del violín o del laud -si os acordáis de lo que os conté aquí de aquel viejo músico Italiano llamado Galileo (sí, el padre del astrónomo)-. Las vibraciones de las cuerdas reales se clasifican a partir de la nota fundamental y de sus armónicos o modos de frecuencia, Las matemáticas de las microcuerdas son similares. Nuestras partículas salen de los modos de frecuencia menor.

No, no será fácil llegar a las respuestas de éstas difíciles preguntas que la física tiene planteadas. Y, sin embargo, ¿cómo podríamos describir lo que en esta teoría ha llegado a causar tanta pasión en esos físicos que llevan años luchando con ella? Recuerdo haber leído aquella conferencia apasionante que dio E. Witten en el Fermilab. Su pasión y forma de encausar los problemas, sus explicaciones, llevaron a todos los presentes a hacerse fervientes y apasionados fans de aquella maravillosa teoría. Todos hablaban subyugados mucho después de que el evento hubiera terminado. Según contó León Lederman, que asistió a aquella conferencia: “Yo nunca había visto nada igual, cuando Witten concluyó su charla, hubo muchos segundos de silencio -¿es mucho?- antes de los aplausos.

Claro que, a medida que la teoría fue topándose con unas matemáticas cada vez más difíciles y una proliferación de direcciones posibles, el progreso y la intensidad que rodeaban a las supercuerdas disminuyeron hasta un nivel más sensato, y ahora, sólo podemos seguir insistiendo y esperar para observar que nos puede traer el futuro de esta teoría que, es posible (y digo sólo posible) que se pueda beneficiar, de alguna manera, de las actividades del LHC que, en algunas de sus incursiones a ese mundo fantasmagórico de lo infinitesimal, podría -y digo podría- atisvar la sombra que puedan producir las supercuerdas.

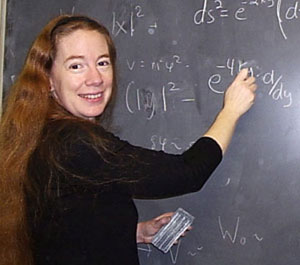
No son pocos los físicos capaces que están empeñados en demostrar esa teoría. Por ejemplo, Físicos de SLAC desarrollan una prueba de marco de trabajo dependiente para la Teoría de Cuerdas Crítica. La Teoría de Cuerdas resuelve muchas de las cuestiones que arruinan la mente de los físicos, pero tiene un problema importante — no hay actualmente ningún método conocido para comprobarla y, si las energías requeridas para ello, es la de Planck  (10¹⁹ GeV), la cosa se pone fea.

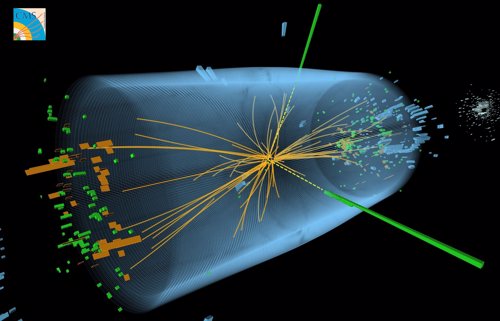
                              ¿Cómo llegsar hasta la energía de Planck?

Lo cierto es que, de momento, sólo es un sueño y, la energía de Planck está muy lejos de nuestro alcance. Poder contar con la energía de Planck, por el momento y durante mucho, mucho, muchísimo tiempo, será sólo un sueño que algunos físicos tienen en la mente. Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.

¡Un universo de Supercuerdas! El sueño de Einstein comienza a tomar realidad, a través de un nuevo paradigma de la ciencia que viene a romper con la toda la visión del mundo y del universo que teníamos hasta ahora, más allá de lo imaginable. Si la Teoría de cuerdas, finalmente resultase ser cierta, ese descubrimiento llevaría al mundo y a la humanidad hasta una nueva dimensión de su propia conciencia.

Habrá que tener paciencia con la Teoría de cuerdas y con el hallazgo tan esperado del Gravitón que nos confirmará, al fín, que la Gravedad como las demás interacciones, también está cuantizada y tiene su Bosón transmisor. De lo que no acabo de estar seguro es…del hecho en sí, de que podamos unir la Gravedad con la Cuántica…¡son tan dispares! y ¡habitan en reinos tan diferentes!

Aunque, ¿qué puedo saber yo?

emilio silvera

[?]

Algunas fórmulas de la Física merecen estar en un lugar destacado para que, cualquiera quen pase por allí las puedan ver y, al ver aquellos jeroglificos matemáticos, poder preguntar por sus significados. Uno de esos casos es el que aquí contamos. Muy justamente, la fórmula a la que nos estamos refiriendo, está inscrita en la cabecera de la lápida que indica el lugar en donde descansan los restos de Ludwig Boltzmann en el cementerio Zentralfriedhof de Viena:

Cuando algo nos gusta y nos atrae, cuando es la curiosidad la que fluía nuestros deseos por saber sobre las cosas del mundo, del Universo y las fuerzas que lo rigen, cuando la Física se lleva dentro al poder reconocer que es el único camino que nos dará esas respuestas deseadas, entonces, amigos míos, los pasos te llevan a esos lugares que, por una u otra razón tienen y guardan los vestigios de aquellas cosas que quieres y admiras. Así me pasó cuando visité el Fermilab, la tumba de Hilbert y, también en Viena, donde no pude resistir la tentación de ver, con mis propios ojos esa imagen de arriba y, desde luego, pensar en lo mucho que significaba la escueta S = k log W que figura en la cabecera de la lápida de Boltzmann como reconocimiento a su ingenio.

[?]

Ese era el título que le puse a una serie de fotografías que, verdaderamente, llaman la atención. Así que, las busqué y traté de ponerlas aquí para ustedes pero, ¡Ah! la sorpresa fue mayúscula cuando al enviarlas, salió la página con los títulos pero sin las fotografías.

Me ví obligado (aquello quedaba feo) a enviar un mensaje al Administrador que, lo quitó.

Pero resulta que, Google, como siempre hace con mis trabajos, sí lo pudo pasar a sus páginas, así que, si lo quereis ver, simplemente teneis que pinchar abajo a la derecha, donde dice: “Suscripciones Web” encima de Google y, las imágenes apareceran por arte de magia.

¿Quién entiende los ordenadores? Yo, desde luego que no.

¡Que disfruteis de las imágenes! ¡Ah! y ya podeis dar las gracias a Kike.

Saludos

[?]