Los ácaros que podemos ver con el microscopio electrónico permite observar sus movimientos: los descubre casi siempre en grupos, semejando divisiones blindadas que  avanzan en formación por paisajes sinuosos y áridos, como desiertos diminutos. Es decir, nos tyenemos que valer de poderosos aparatos electrónicos para poder constatar esa realidad.

Nuestra realidad es que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.

Esas creencias que nos han metido en la mente desde niño son muy poderosas y, despojarnos de ellas, no es cosa fácil. Nos condicionan durante toda la vida y se convierten en ese muro que no nos deja “ver” más allá. En cada sitio y en cada liugar, en cada parte del mundo, tienen sus propias creencias y costumbres y, arrojarlas de nosotros…

                Sí, ambas imágenes son del mismo Tiempo pero, de diferentes lugares y costumbres

Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, para ello observamos y experimentamos, nos fijamos en cómo funciona la Naturaleza a nuestro alrededor y, según la entendemos, tratamos de reflejar, en esos modelos, lo que realmente ocurre. Sin embargo, nuestras perscepciones pueden estar viciadas y, los resultados, no ajustarse a esa realidad que perseguimos.

                          Cada mente esconde su propio mundo

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.

Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas  y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.

En esta aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado. El personaje que aparece a la par, es la persona real. y la que aparece sin pelo es el modelo 3d renderizado. No siempre la realidad está clara ante nuestra vista.

Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:

1 – 1/3 + 1/5 – 1/7 ….

Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente,  se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que  independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y  entre otros temas. Si hablamos de  “Pi” mos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN, el efecto mariposa y la Torah, entre otras muchísimas cosas que  se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes reopresentado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.

No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la teoría del Caos  que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.

El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.

Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.

Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.

¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.

3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th

Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejemplo:

Roger Penrose dedicó bastante más tinta en defender  los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.

Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

                     ¿Es la verdad inalcanzable?

Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.

Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitir nuestros múltiples u dispares pensamientos:

• Los Computadores nunca podrán reemplazar la estupidez humana.
• El hombre nace ignorante,  la educación lo idiotiza.
• Una persona inteligente resuelve problemas, el genio los evita.
• Las mujeres consideran que guardar un secreto, es no revelar la fuente.
• Todas las mujeres tienen algo bonito… así sea una prima lejana.
• La felicidad es una lata de atún, pero con el abrelatas un poco distante.
• El único animal que no resiste aplausos es el mosquito.
• El amor está en el cerebro, no en el corazón.
• Definición de nostalgia “es la alegría de estar triste”.
• “Mi segundo órgano favorito es el cerebro”. Woody Allen.

Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!

Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?

     Todo eso está bien pero, ¿Quien es PI?

Bueno, Pi y Fi encierran todo un mundo de misterios

Desde hace aprox. unos 5000 años, el hombre ha utilizado  objetos que ruedan para ayudarse en sus tareas, por eso es muy probable que haya descubierto ese “3 y pico” hace muchos años, pues es imprescindible para calcular y resolver problemas que involucraran estos cuerpos. Cuenta la historia, que los antiguos egipcios en el 1600 a. de C. ya sabían que existía una relación entre la longitud de la circunferencia y su diámetro; y entre el área del círculo y el diámetro al cuadrado (seguramente de forma intuitiva). En el Papiro de Rhind puede leerse lo siguiente:

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene el mismo área que el circulo”.

Si llamamos A al área del círculo, ésta será igual a 8/9 del diámetro al cuadrado

     A=(8/9 d)^2

Como   d=2r entonces   A= 2r^2 x 64/81  = 4r2 x 64/81  = r2 x 256/81

Así vemos como  π adoptaba el valor 256/81, aproximadamente 3,16.  En Mesopotamia, más o menos por la misma época, los babilonios utilizaban el valor 3,125 (3+1/8) según  la Tablilla de Susa.

Mientras que los geómetras de la Grecia clásica sabían que la razón entre la longitud de una circunferencia cualquiera y su diámetro es siempre una constante (el número al que ahora llamamos pi). También conocían y habían conseguido demostrar que tanto la razón entre el área de un círculo y su diámetro al cuadrado, como la del volumen de una esfera y el cubo de su diámetro eran constantes (desconocidas en aquel momento, libro XII de “Los Elementos” de Euclides).

Fue Arquímedes en el siglo III a. de C. quien determinó que estas constantes estaban estrechamente relacionadas con π. Además, utilizó el método de exhaución, inscribiendo y circunscribiendo en una circunferencia, polígonos de hasta 96 lados y consiguiendo una magnífica aproximación para la época.

Lo cierto es que, desde tiempos inmemoriales, vamos tras la huella del saber, tratando de adentrarnos en el conocimiento de lasd cosas que nos rodean, del mundo en el que vivímos, de la Galaxias que nos acoge y en fin, del Universo y la Naturaleza que guarda todos los secretos que deseamos desvelar y, como nosotros somos parte de esa Naturaleza, es posible, quer todas las respuestas que buscamos esté, desde el principio, gravada en nosotros y, sólo con el tiempo, podrán aflorar y llegar a nuestras mentes que tratan de comprender a veces, con frustración y sufrimiento ante la impotencia de no saber…lo que pueda haber más allá.

emilio silvera

[?]

No es ningún secreto que la obra más famosa de la denominada literatura árabe, Alf Laylah wa-Laylah (Las mil y una noches), era en realidad una antigua obra persa.  Hazar Afsana ( un millar de cuentos), que contenía distintos relatos, muchos de los cuales eran de origen Indio.  Con el paso del tiempo, se hicieron adiciones a esta obra, no sólo a partir de fuentes árabes, sino también griegas, hebreas, turcas y egipcias.  La obra que hemos leído (casi) todos, en realidad, es un compendio de historias y cuentos de distintas nacionalidades, aunque la ambientación que conocemos, es totalmente árabe.

Además de instituciones de carácter académico como la Casa de la Sabiduría, el  Islam desarrolló los hospitales tal como los conocemos hoy en nuestros días.  El primero y más elaborado, fue construido en el siglo VIII bajo al-Rashid (el Califa de Las Mil y una noches),  pero la idea se difundió con rapidez.  Los hospitales musulmanes de la Edad Media que existían en Bagdad, El Cairo o Damasco, por ejemplo, eran bastante complejos para la época.  Tenían salas separadas para hombres y mujeres, salas especiales dedicadas a las enfermedades internas, los desordenes oftálmicos, los padecimientos ortopédicos, las enfermedades mentales y contaban con casa de aislamiento para casos contagiosos.

       Las bibliotecas científicas islámicas tuvieron una enorme influencia en el desarrollo y evolución de la civilización humana hasta que aparecieron con su imagen actual, sin embargo la biblioteca más conocida y famosa de este tipo sin duda fue la Biblioteca “Dar Al Hikmah” (La Casa de la Sabiduría), en Bagdad, que desempeñó el papel más trascendente para el conocimiento en la tierra, sin caer en la más mínima exageración. La Casa de la Sabiduría constituye uno de los tesoros científicos producidos por el pensamiento musulmán en la antigüedad, que también dio lugar a otras muchas bibliotecas científicas en diferentes lugares del Estado islámico, y cuya importante función ha olvidado la gente, a pesar de que ejercieron en aquella época un papel similar al de una universidad científica internacional. Allí acudía todo tipo de alumnos, sin importar su género ni su religión, desde Oriente hasta Occidente, con el fin de estudiar las diferentes disciplinas científicas, en numerosos idiomas. Su luz estuvo iluminando y guiando a la humanidad durante cerca de cinco siglos, hasta que los tártaros la destruyeron.

El Islam, en este campo, también estaba muy avanzado, e incluso tenían clínicas y dispensarios ambulantes y hospitales militares para los ejércitos.  Allí, en aquel ambiente sanitario, surgió la idea de farmacia o apotema, donde los farmaceutas, tenían que aprobar un examen, antes de preparar y recetar medicamentos.

Los conocimientos árabes llegaron hasta Europa a través de España al ser Conquistada por el Islam

La obra de Ibn al-Baytar Al-Jami’fi al-Tibb (Colección de dietas y medicamentos simples) tenía más de un millar de entradas basadas en plantas que el autor había recopilado alrededor de la costa mediterránea.  La noción de sanidad pública también se debe a los árabes que, visitaban las prisiones para detectar y evitar enfermedades contagiosas.

Grandes médicos islámicos como Al-Razi, conocido en occidente por su nombre latino, Rhazes, nació en la ciudad persa de Rayy y en su juventud fue alquimista, después de lo cual se convirtió en erudito en distintas materias.  Escribió cerca de doscientos libros, y aunque la mitad de su obra está centrada en la medicina, también se ocupó de temas teológicos, matemáticos y astronómicos. ¡Todo un personaje! Fue el primer médico Jefe del gran hospital de Bagdad.  Se dice que para elegir el sitio de ubicación del hospital, primero colgó tiras de carne en distintos lugares de la ciudad, y, finalmente eligió aquel donde la carne era menos putrefacta.

La gran obra de al-Razi fue el AL-Hawi (El libro exhaustivo), una enciclopedia de veintitrés volúmenes de conocimientos médicos griegos, árabes, preislámicos, indios e incluso chinos.

El otro gran médico musulmán fue Ibn Sina, a quien conocemos mejor por su nombre latinizado, Avicena.  Al igual que al-Razi, Avicena escribio doscientos libros, destacando la obra más famosa AL-Qanun (El canon) muy documentado e importante tratado.

Alejandría, en el año 641, había caído en manos de los musulmanes que, durante muchos años había sido la ciudad capital-mundial de los estudios matemáticos, médicos y filósofos, y allí los musulmanes encontraron una ingente cantidad de libros y manuscritos griegos sobre estos temas.  Posteriormente, entre el profesorado de la Casa de la Sabiduría encontramos a un astrónomo y matemático cuyo nombre, como el de Euclides, se convertiría en palabra de uso cotidiano en todo el mundo culto: Muhammad ibn-Musa aL-khwarizmi.

La fama de al-khwarizmi descansa en dos libros, uno muchísimo más original que el otro.  El volumen menos original se basa en el Sindhind, que es el nombre árabe del Brahmaghuta Siddhanta, el tratado de Brahmagupta que había llegado hasta la corte de al-Mansur y en el que se describen varios problemas aritméticos así comos los numerales indios.  El trabajo de AL-khwarizmi se conoce hoy en una única copia, una traducción latina de un original árabe actualmente perdido.

El título latino de esta obra es de numero indorum (sobre el arte de contar indio), este trabajo es el responsable de la falsa impresión de que nuestro sistema numérico es de origen árabe.

al-khwarizmi no afirmó ser original en aquel sentido, sin embargo, la nueva notación terminaría siendo conocida como la de al-khwarizmi o, de forma corrupta, algorismi, lo que al final daría lugar a la palabra “algoritmo”, que define una forma particular de calculo.

Pero al-khwarizmi también es conocido como el “padre del álgebra” y, ciertamente, su Hisab aL-jabr wa’L mugabalah contiene más de ochocientos ejemplos y, se cree que tiene su origen en complejas leyes islámicas relativas a la herencia:

¡La forma en  que evolucionaron los números!

En el al-jabr, aL-khwarizmi introduce la idea de representar una cantidad desconocida por un símbolo, como la x, y dedica seis capítulos a resolver los seis tipos de ecuaciones que conforman las tres clases de cantidades: raíces, cuadrados y números.

El al-jabr de al-khwarizmi ha sido considerado tradicionalmente como la primera obra de Algebra.  Sin embargo, un manuscrito hallado en Turquía a finales del pasado siglo XX pone en duda tal mérito.  Se titula Necesidades lógicas en las ecuaciones mixtas, el texto se ocupa más o menos de los mismos temas y resuelve algunas de las ecuaciones exactamente de la misma manera.  Por tanto, parece que un manuscrito se basó en otro, aunque nadie sabe cuál fue el primero.

En las ciencias químicas, la personalidad árabe más destacada fue Jabir ibn-Hayyan, conocido en Occidente como Geber, y quien vivió en aL-kufah en la segunda mitad del siglo VIII.

Como todos en la época, él también estaba obsesionado con la alquimia y, en particular, por la posibilidad de convertir los metales en oro (algo que Jabir pensaba podía conseguir mediante una misteriosa sustancia aún no descubierta, a la que llamó, el aliksir, de donde proviene la palabra “elixir”).  Los alquimistas también creían que su disciplina era la “ciencia del equilibrio” y que era posible producir metales preciosos mediante la observación (y mejoramiento) de los métodos de la naturaleza mediante la experimentación y, es legitimo considerar a Jabir uno de los fundadores de la química.

Paralelamente a esto, aL-Razi ofreció una clasificación sistemática de los productos de la naturaleza.  Dividió las sustancias minerales en espíritus (mercurio, sal amoníaco), sustancias (oro, cobre, hierro), piedras (hermatites, óxido de hierro, vidrio, malaquita), vitriolos (alumbre), Góraxes y sales.  A estas sustancias “naturales” añadió las “artificiales”:  el cardenillo, el cinabrio, la soda cáustica, las aleaciones.  aL-Razi también creía en lo que podríamos denominar investigación de laboratorio y desempeñó un importante papel en la separación de la química propiamente dicha de la alquimia.

¡Son tantas las cosas que podemos recordar de tiempos pasados!

Si podeis, os recomiendo la lectura del libro “Ideas” de Peter Watson, en él podreis encontrar relatos que, como el que arriba habeis leído, os llevará al pasado y os contará maravillas, muchas veces olvidadas y que, en realidad, forjaron la senda para que nosotros pudiéramos llegar hasta aquí.

emilio silvera

[?]

Representar un Agujero negro no resulta nada fácil y, se hace de manera que aparezca en la imagen lo que se cree que podríamos ver en el caso de estar allí cerca, contemplando a uno de ellos, y, como existen varias formas teóricamente posibles de agujero negro, las representaciones que podemos contemplar pueden ser distintas las unas de las otras.

Según sean estrellas medianas como nuestro Sol, grandes o muy grandes, lo que antes era una estrella, cuando finaliza el derrumbe o implosión, cuando la estrella es aplastada sobre sí misma bajo su propio peso, cuando finalice su ciclo y consuma todo el combustible nuclear que la hace brillar, tendremos una estrella enana blanca, una estrella de neutrones o un agujero negro.

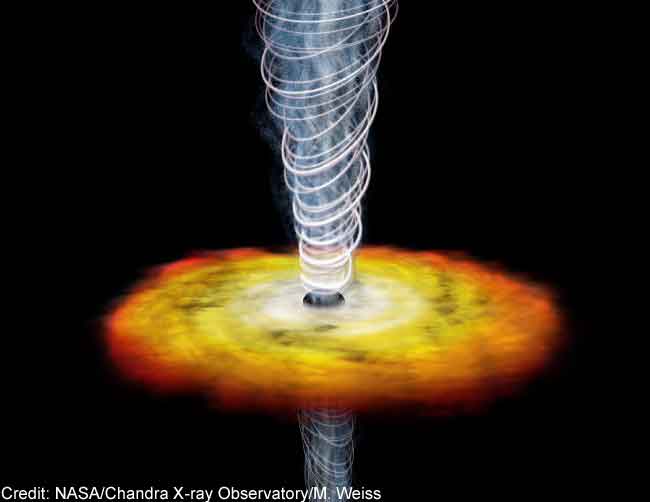
Alrededor del agujero negro puede formarse un disco de acreción cuando cae materia sobre él desde una estrella cercana que, para su mal,  se atreve a traspasar el horizonte de sucesos. Es tan enorme la fuerza de gravedad que genera el agujero negro que, en tal circunstancias, literalmente hablando se come a esa estrella compañera próxima. En ese proceso, el agujero negro produce energía predominantemente en longitudes de onda de rayos X a medida que la materia está siendo engullida hacia la singularidad.  De hecho, estos rayos X pueden ser detectados por satélites en órbita. Se ha localizado una enorme fuente de rayos X en el centro mismo de nuestra galaxia. En realidad han sido varias las fuentes localizadas allí, a unos 30.000 años luz de nosotros. Son serios candidatos a agujeros negros, siendo el más famoso Cygnus X-1.

Existen varias formas teóricamente posibles de agujeros negros.

• Un agujero negro sin rotación ni carga eléctrica (Schwarzschild).
• Un agujero negro sin rotación con carga eléctrica (Reissner-Nordström).

[?]

Nosotros, los humanos, nacemos y morimos. Esa es la regla, y, como desde el primer momento de nuestras vidas se ha puesto en marcha “un reloj” que estará con nosotros hasta el día último, parece que vamos siempre en contra del Tiempo, que nunca tendremos la oportunidad de realizar todos nuestros deseos y aspiraciones y, siempre tendremos que dejar que otros continúen el trabajo que, por otra parte, tampoco nosotros iniciamos, sino que, retomamos de aquellos otros que antes que nosotros estuvieron aquí y nos marcaron el camino a seguir. Es una larga cadena de hechos, de acontecimientos y de evolución que no sabemos cuando ni por qué finalizará un día lejano del futuro que presentimos pero que, con certerza, no conocemos.

Desde siempre, los grandes filósofos se sintieron frustados al comprender que, nuestra estancia aquí, sería limitada. El ser que se ve arriba en la imagen dicen que buscaba el motor de la vida pero, nosotros, sabiendo ya el origen de ese motor, buscamos otras respuestas que nadie nos sabe contestar y, hemos llegado a comprender que, en este Universo que nos acoge, todo tiene un principio y un final, nada permanece, lo infinito y la eternidad son sólo palabras que quieren significar “el para siempre” en que todos pensamos para la Humanidad. Sin embargo, la misma dinámica y el ritmo del Universo nos lleva de manera irremisible, hacia el final.

[?]