¿Definir la Ciencia? No será fácil en un campo tan inmenso

Para lo que este simple comentario trata de reflejar, bastaría decir que la Ciencia es un estudio lógico y sistemático de la Naturaleza y del mundo físico que abarca todo el Universo y todo lo que dentro de él está presente. Generalmente incluye tanto experimento como teorías que son verificadas por aquellos.

 ’El túnel de la ciencia’, en el Museo de Artes e Historia del Forum Cultural de Guanajuato. México

La ciencia (del Latín scientia “conocimiento”) es el conjunto de conocimientos sistemáticamente estructurados, y susceptibles de ser articulados unos con otros hasta formar un todo en un entendimiento “general” de la Naturaleza del Universo.

Aunque la definición pueda resultar algo floja, es, sin embargo un compendio general de lo que entendemos por ciencia. Más arriba escribo “generalmente” en cursiva, porque si planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recrear nuevas estrellas o galaxias en Laboratorio, ni escenificar la creación del sistema solar. Sin embargo, en Astronomía las observaciones son a menudo tan valiosas como los mismos experimentos. El Cometa Halley regresa con una regularidad sorprendente; el Sol sale cada mañana.

El filósofo Karl Popper añadió el requisito de la “refutación” La Ciencia es refutable; la Religión no lo es. Una Teoría o una Ley científica nunca pueden ser demostradas de manera absoluta; de ahí que sea posible refutarlas. Por ejemplo, Newton dijo que la fuerza es igual al producto de la masa por la aceleración (D = ma). No podemos demostrar que todos los objetos de todas las galaxias obedecen esta ley o que todos los objetos obedecerán siempre esta Ley. Sin embargo, para demostrar la falsedad de esta Ley bastaría un solo experimento. (Albert Einstein y varios expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos.) Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal como afirmó Popper. Estas Teorías han de ser comprobables. No existe tal requisito en el caso de la Religión.

                                                 La Mente Humana está en conexión con el Universo

Dicho esto, sigue habiendo problemas con la definición. La Astrología, por ejemplo, es refutable. Si nuestros astrólogos nos dicen que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse. Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría del todo”, requeriría un acelerador de partículas con un diámetro de diez años-luz para poder refutarla. La mayor parte de la Biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una especie, ni recrear los dinosaurios comenzando con un animal unicelular. Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas e incluso quizá la Astronomía.

En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la “refutación” del filósofo de la Ciencia, ya que, de otro modo, podríamos vernos obligados a excluir toda la Ciencia de los antiguos griegos. Estos no sólo eludían el experimento, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.

Yo, sí he llegado a tener mi propia definición de la Ciencia: “Es el estudio que nos lleva, a través de la observación y el experimento, a la verdadera realidad de la Naturaleza, y, para ello, utilizamos nuestra imaginación para construir modelos y teorías que nos acerquen a esa verdad que presentimos y tratamos de desvelar”.

Los que bebemos de la Ciencia, sentimos que “lo divino” se aleja más y más. Sin embargo, no podemos dejar de sentir que, de alguna manera, algo superior nos vigila, yo lo achaco a ese miedo ancestral que, desde siempre, hemos tenido por lo desconocido y que, inmerso en una profunda ignorancia, no pocas veces hemos querido explicar mediante causas “divinas”, y, sin embargo, cuando, finalmente, hemos dado con las respuestas, estas eran de este mundo y, siempre, eran respuestas lógicas que la Naturaleza nos ofrecía y que no sabíamos compreneder.“ ¿El Creador? Es el Universo con sus complejos sistemas de ritmos y energías el que nos lleva hacia ese futuro que deseamos alcanzar. No existe ningún creador.

Bueno, la definición que de la Ciencia hago y reseño encima de la imagen de arrina, no será perfecta pero, para cumplir los objetivos propuestos es válida y suficiente aunque (como es el caso) le falten algunos matices.

Aquí, en esta página, siempre nos hemos limitado a aquellas disciplinas más estrictas: La Física, La Astronomía, La Cosmología, La Geología, La Química y La Tecnología, Sin olvidar las matemáticas, ya que son indispensables para la Ciencia y están ineludiblemente conexionada con todas ellas que, de una u otra manera, las necesita para poder expresar, en su más alto grado, lo más profundo que esa Ciencia nos quiere decir. Es decir, las matemáticas son el lenguaje del que se vale la Ciencia para decir al mundo lo que realmente son en cada una de sus vertientes. He dejado aparte y sin querer tratar de ellas, las disciplinas más ligeras –La Antropología, La Agronomía, La Psicología, La Medicina y otras del mismo estilo o parecidas- para otros momentos.

Alguna vez, queriendo hablar de ciencia…nos salimos de ella

Algo que nunca he tomado en consideración ha sido el pragmatismo de la Ciencia o la motivación de los científicos. Estas cuestiones se han utilizado a menudo para desacreditar las Ciencias no occidentales: sí es un trabajo bien hecho, pero no es “puro”, o, a la inversa, no resulta práctico. En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por la religión: los matemáticos árabes perfeccionaron el álgebra en parte para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas. En estos casos la Ciencia estuvo al servicio de la religión, pero no obstante era Ciencia.

La ley de los epónimos de Stigler, formulada por el experto en estadística Stephen Stigler, afirma que ningún descubrimiento científico lleva el nombre de su descubridor original. El periodista Jim Holt indica que la propia Ley Stigler confirma lo que dice, ya que Stigler admite que la Ley que lleva su nombre fue descubierta por otra persona, concretamente por Robert K. Merton, un especialista en Sociología de la Ciencia.

El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Entre todos los casos en que se cumple la Ley de Stigler, el más famoso es el del Teorema de Pitágoras (a²+ b² = c², donde a y b son los lados perpendiculares y c es la hipotenusa). Jakob Bronowski escribe lo siguiente:

“Hasta la fecha, el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse (de hecho se ha hecho) a planetas de otros sistemas estelares a modo de test, para comprobar si estos planetas tienen ocupación debida a seres dotados de vida racional.

                  La placa con el mensaje que llevan la Pioneer 10 y 11

Claro que el problema está en que no fue Pitágoras el primero que propuso “su” teorema. Los hindúes, los egipcios y los babilonios utilizaban “tríos de números pitagóricos” para determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. El trío más habitual es 3 : 4 : 5 (3² + 4² = 5² o 9 + 16 = 25). Pitágoras “inventó” este teorema hacia el año 550 a. C. Los Babilonios, según todos los indicios, ya habían catalogado quizá cientos de tríos antes del año 2000 a. C., en una época muy anterior a la de Pitágoras. Uno de los tríos que hallaron los babilonios tienen unos números tan enormes como: 3.367 : 3.456 : 4.825.”

                                                ¡La Imaginación! ¿Qué barreras puede tener?

El ojo humano tiene sus limitaciones para ver, sin embargo, la imaginación no tiene barreras y, a lo largo de la historia de la Humanidad se han dado pruebas de lo lejos que pueden llegar nuestros pensamientos.Los Babilonios, egipcios e Hindúes le dejaron un campo sembrado a Pitágoras que, en realidad, sólo tuvo que recoger la abundante cosecha. Él sí supo “ver”.

Ahí están y  existen indicios de que los babilonios utilizaron diversas técnicas algebraicas derivadas de la fórmula a² + b² = c². Lo que puede reconocerse como un logro de Pitágoras, que impresionó a muchos, fue la elaboración de una demostración geométrica del teorema…  El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Fue Euclides quien proclamó dos siglos más tardes la idea de que la demostración podía ser algo más importante que el propio teorema. Por consiguiente, las matemáticas no occidentales han quedado consideradas como unas matemáticas de segunda categoría debido a que se apoyan sobre una base empírica y no sobre demostraciones.

Ambos métodos son útiles. La Geometría euclidiana que aprendimos la mayoría de nosotros es axiomática. Parte de un axioma, es decir, una ley que se supone cierta, y los teoremas se deducen razonando de manera descendente a partir de ahí. Es deductiva y axiomática. Siglos más tarde, al-Hazin en Oriente y Galileo en Occidente contribuyeron a popularizar un método inductivo y empírico para la Ciencia, algo más parecido a lo que los babilonios, los egipcios y los hindúes habían utilizado. No se parte de suposiciones sino de datos y mediciones, para luego razonar de forma ascendente hacia verdades que recubren los datos conocidos. Lo que actualmente llamamos Ciencia es una materia que en su mayor parte es empírica. Cuando Isaac Newton recopiló datos relativos al paso de los cometas, a las lunas de Júpiter y de Saturno y a las mareas que se producían en el estudio del río Támesis para elaborar una gran síntesis en los Principia, estaba trabajando de una manera empírica e inductiva.

Las matemáticas son ligeramente diferentes, pero muchos matemáticos ven la necesidad de realizar tanto trabajos basados en las demostraciones como trabajos basados en las observaciones empíricas. Un caso puntero que podemos mencionar es el del gran matemático indio Srinivasa Ramanujan, cuyos “cuadernos perdidos” de anotaciones contienen el germen de la teoría de las supercuerdas y cuyos trabajos han sido utilizados para calcular el número π hasta millones de dígitos en su parte decimal.

Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Es ahí, donde la Teoría se hace fuerte y nos facilita la posibilidad de continuar su desarrollo.

Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un número único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos para explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares (¿Las de Ramanujan?).

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.

Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

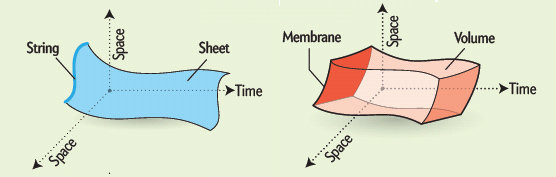
Una partícula, una cuerda abierta y
una cerrada, describiendo sus órbitas en el
espacio-tiempo 4D.

El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.

Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se les esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Una interacción general entre cuerdas se puede representar como la suma de interacciones más “elementales”, empezando con el diagrama árbol que representa la interacción con la mayor probabilidad de ocurrir, seguida por las correcciones perturbativas, es decir, por los demás diagramas de la serie infinita. Como puede observarse en dicha figura, las superficies que representan las interacciones no se vuelven increiblemente complicadas como los digramas de partículas, ya que sólo hay que agregarle agujeros a una superficie dada.

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista A_µ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Ramanujan en Cambridge

Con tan solo doce años dominaba la trigonometría; unos años después se hizo con una copia del libro de George Carr <<A sinopsis of Elementary Results in Pure and Applied Mathematics>>. El libro contenía una lista de los 4.400 resultados clásicos de la matemática, pero sin demostraciones, así es que Ramanujan lo asumió como un reto. Durante los siguientes años se dedicó a fondo en este libro, y comenzó a llenar su libreta de resultados e ideas que no aparecían en el libro original. Al igual que Euler poseía un talento y una intuición excepcional, esto hacía que jugase y trasformarse las fórmulas hasta conseguir nuevas perspectivas.

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.

Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.

Está claro que, este simple comentario no explica lo que la Ciencia es y, desde luego, tendríamos que ir a una complejidad mucho más profunda y elevada para poder hablar de algunas ramas de la Ciencia que requieren de un nivel de comprensión de la Naturaleza que, de ninguna manera poseo. ¿Cómo he terminado este trabajo como lo he hecho? Empecé con una intención y, por el camino, como si tuviera vida propia, los pensamientos te llevan por otros senderos que, nunca habías pensado recorrer. ¡Qué cosas!

emilio silvera

[?]