La Naturaleza está en nuestras Mentes

“Así fue como ví el péndulo

La esfera, colgando de un largo cable fino al techo del

coro, oscilaba de un lado a otro con una majestád isócrona.

Yo sabía -pero cualquiera podía haberlo sentido en la

magia de ese sereno aliento- que el período estaba gobernado

por la raíz cuadrada de la longitud del cable y por π,

ese número que, por irracional que sea para las mentes sublunares,

liga la circunferencia y el diámetro de todos los cículos posibles a

través de una racionalidad superior. El tiempo que necesitaba la

esfera para oscilar de un extremo a otro estaba determinado por una

conspiración arcana entre la más intemporal de las medidas: la singularidad

del punto de suspensión, la dualidad de las dimensiones del plano, el

comienzo triádico de π, la secreta Naturaleza cuadrática de la raíz y la

innumerada perfección del propio círculo.”

Uberto Eco

Después de haber utilizado durante un tiempo las ecuaciones y fórmulas de la física matemática, uno se acostumbra a una peculiaridad de la Naturaleza. Es muy comprensica con nuestra ignorancia de ciertos detalles. Las leyes de la Naturaleza tienen varios ingredientes: una máquina lógica para predecir el futuro a partir del presente, constantes especiales de la Naturaleza y un conjunto de simples números. Estos simples números aparecen junto a las constantes de la Naturaleza en casi todas las fórmulas físicas.

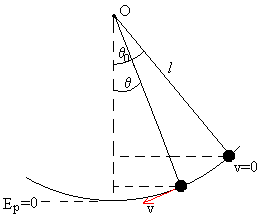
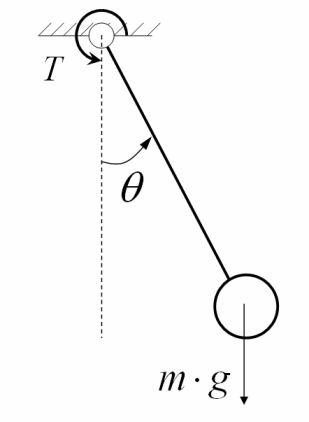
Einstein los supo apreciar muy bien y así lo reflejaba en las cartas que le envió a su amiga Ilse Rosenthal Schneider y los lamaba “constantes básicas”. Son solamente números. Por ejemplo, el período (“tic”) de un reloj de péndulo estaba dado con gran precisión por una sencilla fórmula:

Período = 2π √(L/g)

Donde L es la longitud del péndulo y g es la aceleración de la gravedad en la superficie de la Tierra. Aquí podemos notar la aparición de la “constante básica” 2π = 6,28. En todas las fórmulas que utilizamos para describir algún aspecto del mundo físico, aparece un factor numérico de este tipo. Lo más notable es que casi siempre tienen un valor próximo a uno y pueden despreciarse, o aproximarse por 1, si sólo se está interesado en obtener una estimación razonablemente buena del resultado.

Éste es un premio importante, porque en un problema como la determinación  del período de un péndulo simple nos permite obtener la forma aproximada de la respuesta.. El período, que tiene dimensiones de tiempo, sólo puede depender de una manera de la longitud L y la aceleración g si la combinación resultante ha de ser un tiempo: esa combinación es la raíz cuadrada de L/g.

Esta bonita característica del mundo físico, que parece estar bien descrito por leyes matemáticas en las que los factores puramente numéricos que aparecen no son muy diferentes de 1 en magnitud, es uno de los misterios casi desapercibidos de nuestro estudio del mundo físico. Einstein estaba muy impresionado por la ubicuidad de pequeños números adimensionales en las ecuaciones de la física y escribió sobre el misterio de que, aunque casi siempre parece ser así.

“…no podemos exigirlo rigurosamente, pues ¿por qué no debería aparecer un factor numérico como (12π)³ en una deducción fisicomatemática? Pero sin duda tales casos son rarezas.”

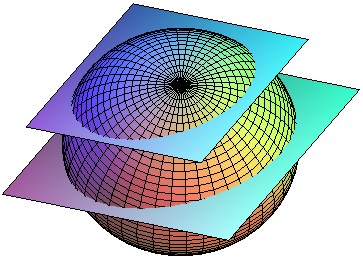
Es posible arrojar alguna luz sobre este problema si reconocemos que casi todos los factores numéricos por los que Einstein estaba tan impresionado tienen un origen geométrico. Por ejemplo, el volumen de un cubo de arista R es R³, pero el volumen de una esfera de radio R es 4πR³/3. Los factores numéricos dan cuenta de la forma detallada cuando las fuerzas de la Naturaleza estan actuando. Puesto que las fuerzas fundamentales de la Naturaleza son simétricas y no tienen una preferencia por direcciones diferentes, hay una tendencia a la simetría esférica.

                                                   Nuestra Galaxia, el Sol y nuestro mundo y la Luna… ¡Todos tienden a ser esféricos!

Nos hemos podido dar cuenta de que a partir de todo lo que hemos podido aprender, hemos podido ver que las constantes de la Naturaleza tienen una influencia relativa mucho mayor  cuando se trata de determinar los resultados de las leyes de la Naturaleza en tres dimensiones que la que tienen en universos con muchas más dimensiones espaciales.

Cuando consideramos mundos con dimensiones de espacio y tiempo distintas de 3 + 1 topamos con un problema sorprendente. Los mundos con más de una dimensión no permiten predecir el futuro a partir del presente. En este sentido son más bien como mundos sin dimensión temporal. Un sistema organizado complejo, como, por ejemplo, el necesario para la vida, no podría utilizar la información recogida en su entorno para conformar su comportamiento futuro. Seguiría siendo simple: demasiado simple para almacenar información y evolucionar.

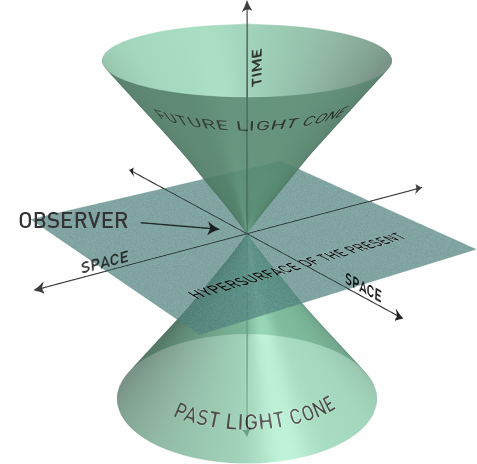
Si el número de dimensiones de espacio y tiempo hubiera sido escogido aleatoriamente y todos los números fueran posibles, entonces esperaríamos que el número fuera muy grande. Es muy improbable escoger un número pequeño. Sin embargo, las ligaduras impuestas por la necesidad de tener “observadores” para hablar del problema significa que no todas las posibilidades están disponibles y que se nos impone un espacio tridimensional. Todas las alternativas estarían privadas de vida. Si científicos de otro universo conocieran nuestras leyes pero no el número de dimensiones en que vivimos, podrían deducir su número simplemente a partir del hecho de nuestra existencia.

Así que, si queremos hacer una aproximación al problema de por qué el espacio tiene tres dimensiones,  nos lleva a una estimación de gran alcance de cómo y por qué son peculiares los mundos tridimensionales con una única flecha del tiempo. Las alternativas son demasiado simples, demasiado inestables o demasiado impredecibles para que observadores complejos evolucionen y perduren dentro de ellos. Como resultado, no debería sorprendernos encontrarnos viviendo en tres dimensiones espaciales sujetos a los caprichos de un único tiempo. No par4ece que existan alternativas.

Y, a todo esto, ustedes se preguntarán: ¿Qué tiene que ver todo esto con el péndulo? Bueno, ya sabéis que todo evoluciona y, a medida que se va escribiendo parece que las ideas fluyen y también evolucionan en su transcurrir de manera tal que, de una cuestión se pasa a otra sin que lo podamos evitar.

Le doy desde aquí las gracias a John D. Narrow que, con sus ideas inspiró ésta página para que todos pudiéramos disfrutar al acercarnos al conocimiento de las cosas, del mundo, del universo y de su Naturaleza que continuamente nos enseña por qué camino debemos seguir avanzando.

emilio silvera

[?]