Las energías, el Universo, y, nosotros que observamos.

En concreto, la energía es una cantidad que depende de cómo midamos las distancias y los intervalos de tiempo. Un automóvil de prueba que choca a gran velocidad contra una pared de ladrillos tiene obviamente energía. No obstante, si el veloz automóvil se aproxima a la velocidad de la luz, sus propiedades de distorsionan. Se contrae como un acordeón y los relojes en su interior se frenan. Lo que es más importante, Einstein descubrió que la masa del automóvil también aumenta cuando se acelera. Pero, ¿de dónde procede este exceso de masa?, y él concluyó que procedía de la energía.

La teoría desarrolla un sistema de matemáticas con el fin de reconciliar estas afirmaciones en aparente conflicto. Una conclusión de la teoría es que la masa de un cuerpo, m, aumenta con su velocidad, v, de acuerdo con la relación:

donde m₀ es la masa en reposo del cuerpo. Einstein también concluyó que si un cuerpo pierde energía L, su masa disminuirá en L/c². Einstein generalizó esta conclusión al importante postulado de que la masa de un cuerpo es una medida de su contenido en energía, de acuerdo con su ecuación m=E/c² que, en su versión más conocida es E=mc².

Esto tuvo consecuencias perturbadoras. Dos de los grandes descubrimientos de la física del siglo XIX fueron la conservación de la masa y la conservación de la energía; es decir, la masa total y la energía total de un sistema cerrado, tomados por separado, no cambian. Por ejemplo, si el coche veloz choca contra el muro de ladrillos, la energía del automóvil no desaparece, sino que se convierte en energía sonora del choque, energía cinética de los fragmentos de ladrillo que vuelan por los aires, energía calorífica, y así sucesivamente. La energía total (y la masa total) antes y después del choque es la misma.

Sin embargo, Einstein decía ahora que la energía del automóvil podría convertirse en masa (un nuevo principio de conservación que decía que la suma total de la masa y la energía debe siempre permanecer constante). La materia no desaparece repentinamente, ni la energía brota de la nada. En este sentido, la materia desaparece sólo para liberar enormes cantidades de energía o viceversa.

Cuando Einstein tenía 26 años, calculó exactamente cómo debía cambiar la energía si el principio de la relatividad era correcto, y descubrió la relación E = mc². Puesto que la velocidad de la luz al cuadrado (c²) es un número astronómicamente grande, una pequeña cantidad de materia puede liberar una enorme cantidad de energía. Dentro de las partículas más pequeñas de materia hay un almacén de energía, más de un millón de veces la energía liberada en una explosión química. La materia, en cierto sentido, puede verse como un depósito casi inagotable de energía; es decir, la materia es en realidad energía condensada.

Einstein supo ver que las dimensiones más altas tienen un propósito: unificar los principios de la naturaleza. Al añadir dimensiones más altas podía unir conceptos físicos que, en un mundo tridimensional, no tienen relación, tales como la materia y la energía o el espacio y el tiempo, que gracias a la cuarta dimensión de la relatividad especial, quedaron unificados.

Desde entonces, estos conceptos los tenemos que clasificar no por separado, sino siempre juntos como dos aspectos de un mismo ente materia-energía por una parte y espacio-tiempo por otra. El impacto directo del trabajo de Einstein sobre la cuarta dimensión fue, por supuesto, la bomba de hidrógeno, que se ha mostrado la más poderosa creación de la ciencia del siglo XX, claro que en contra del criterio de Einstein, que era pacifista y nunca quiso participar en proyectos de esta índole.

Einstein completó su teoría de la relatividad con un segundo trabajo, que al menos en parte, estaba inspirado por lo que se conoce como principio de Mach; la guía que usó Einstein para crear esta secuela final y completar su teoría de la relatividad general.

Einstein enunció que la presencia de materia-energía determina la curvatura del espacio-tiempo a su alrededor. Ésta es la esencia del principio físico que Riemann no logró descubrir: la curvatura del espacio está directamente relacionada con la cantidad de energía y materia contenida en dicho espacio. Esto, a su vez, puede resumirse en la famosa ecuación de Einstein, que se denota:

Esta ecuación engañosamente corta es uno de los mayores triunfos de la mente humana. De ella emergen los principios que hay tras los movimientos de las estrellas y galaxias, los agujeros negros, el Big Bang, y seguramente, el propio destino del universo.

Es curiosa la similitud que se da entre la teoría del electromagnetismo y la relatividad general; mientras que Faraday experimentó y sabía los resultados, no sabía expresarlos mediante las matemáticas, y apareció Maxwell que finalmente formuló la teoría.

Einstein, al igual que Faraday, había descubierto los principios físicos correctos, pero carecía de un formulismo matemático riguroso suficientemente potente para expresarlo (claro que Faraday no era matemático, y Einstein sí lo era). Carecía de una versión de los campos de Faraday para la gravedad. Irónicamente, Riemann tenía el aparato matemático, pero no el principio físico guía, al contrario que Einstein. Así que finalmente fue Einstein el que pudo formular la teoría con las matemáticas de Riemann.

Faraday y Maxwell

“¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la naturaleza marcará una discontinuidad en la historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna del siglo XVII. ¿Podemos imaginar ahora cómo sería?”

Steven Weinberg

¿Es la belleza un principio físico?

La teoría de supercuerdas nos da una formulación convincente de la teoría del universo, sin embargo, el problema fundamental radica en que una comprobación de dicha teoría está más allá de nuestras posibilidades actuales. De hecho, la misma teoría predice que la unificación de todas las fuerzas ocurre a la energía de Planck, o 10¹⁶ miles de millones de electronvoltios, que como sabéis, es alrededor de mil billones de veces mayor que las energía actualmente disponibles en nuestros aceleradores de partículas.

Ya he comentado otras veces que el físico David Gross (el de más edad de los miembros conocidos como el cuarteto de cuerdas y autores de la teoría llamada la cuerda heterótica) dijo en una ocasión: “El coste de generar esta fantástica energía necesitaría el dinero de las tesorerías de todos los países del mundo juntos, y quizá no llegara. Es verdaderamente astronómico.“

Siendo así, de momento estamos condenados a no poder verificar experimentalmente este motor (parado) que haría marchar el vehículo de la física. La teoría decadimensional está paralizada en dos sentidos: el económico y técnico y el matemático. El primero por falta de dinero que nos pudiera construir aceleradores tan potentes (el LHC sólo cumple parte de nuestros deseos) como para descubrir la partícula de Higgs, los quarks e incluso las cuerdas vibrantes, esos previsibles y minúsculos objetos primordiales que conforman la materia. En segundo lugar, las formulaciones matemáticas complejas que, según parece, aún no se han inventado. Parece que hoy, ni siquiera Witten o Perelman conocen el secreto de los números mágicos que nos puedan llevar hasta el final del camino iniciado por Einstein y Kaluza-Klein.

Aunque llegar hasta las cuerdas no será nada fácil, particularmente opino que la teoría de cuerdas nos dará muchas alegrías y que en ella están las respuestas a muchas preguntas que no sabemos contestar. Es cierto que no puede ser verificada al tener la energía necesaria para ello. Sin embargo, hay indicios de que las cuerdas pueden estar ahí, a la espera de que las podamos encontrar.

Dentro del mundo de la física los hay de todas las opiniones: en contra y a favor. Es famosa la postura detractora del Nobel Sheldon Glashow de Harvard; no quiere ni oír hablar de la teoría de supercuerdas a la que califica de física de teatro.

Otros muchos, la mayoría, como Murray Gell-Mann, Steven Weinberg (ambos premios Nobel) o el mismo E. Witten (medalla Field), opinan lo contrario y ven en esta teoría de dimensiones más altas el futuro de la física. Simplemte se trata de que, dicha teoría, nos ha llegado por casualidad mucho antes de lo que correspondía.

Los trabajos de Gabriele Veneziano (Florencia, 1942) son pioneros en uno de los temas estrella de la física teórica, la teoría de cuerdas, que permite desarrollar escenarios alternativos al Big Bang, mediante la existencia del tiempo y del espacio desde siempre.

La teoría de cuerdas se inventó a finales de los sesenta, y pasados los años se ha visto que era un escenario donde era posible describir al mismo tiempo la materia, el espacio y el tiempo, y de esa manera resolver un problema que se plantea en la teoría de la relatividad de Einstein. El mismo Einstein dedicó muchos años a intentar reconciliar su teoría de la relatividad con la mecánica cuántica. No lo consiguió, en su tiempo ni existían las matemáticas necesarias para ello, y, de hecho, aún seguimos esperando que aparezcan.

Ya sabemos que en física toda teoría debe ser verificada, una y otra vez, en uno y otro lugar, experimentalmente, obteniendo siempre el mismo resultado; es la única manera de que sea aceptada por la comunidad científica. Mientras tanto, la teoría no es fiable y queda a la espera de ser comprobada, verificada sin ningún lugar para la duda.

Pero, ¿se puede recrear la creación?

La teoría de supercuerdas trata de eso. Quiere explicarnos todos los misterios del universo a partir de ese primer momento, ¡la creación! ¿Cuántas y cuántas páginas no habré leído y escrito sobre estos temas fascinantes de los secretos del universo, las fuerzas que lo rigen, la materia de las galaxias y de los objetos que lo pueblan? No podría decirlo. Sin embargo, hay una cosa que sí puedo decir: ¡cuanto más profundizo en estas cuestiones, cuanto más conocimientos adquiero, más fascinación siento, y desde luego, mi capacidad de asombro persiste!

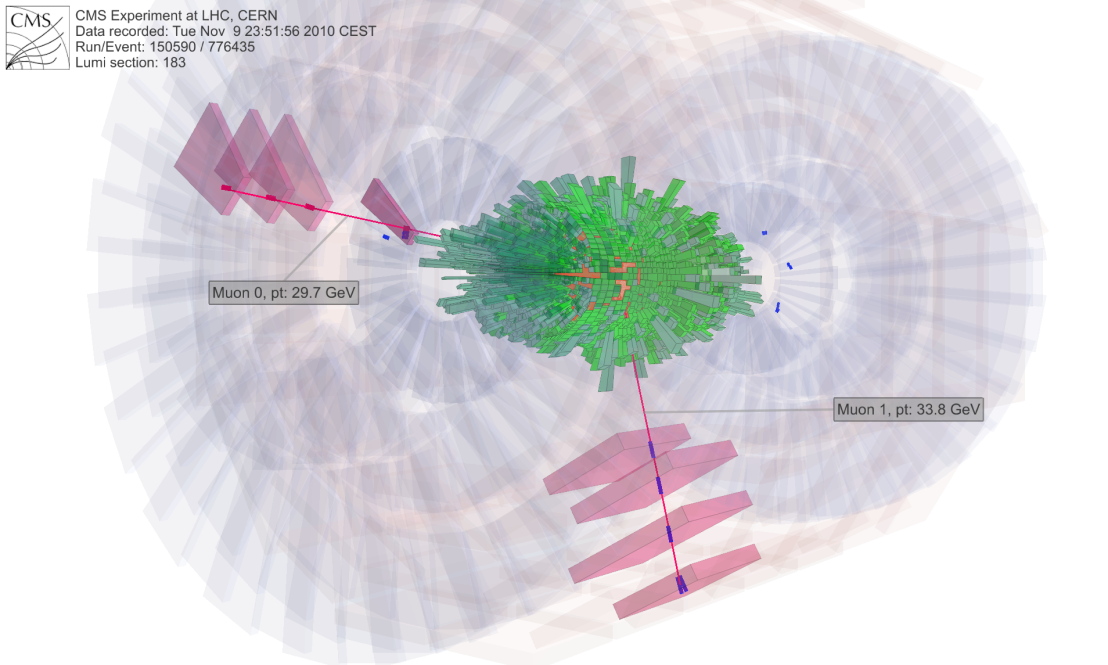
El LHC no es suficiente para generar las energías necesarias para llegar a las cuerdas

Qué lástima que no se construya un supercolisionador superconductor , que encontrara los vestigios subatómicos que mostrara una señal característica de la supercuerda, tal como la supersimetría. Claro que, no creo que hoy por hoy podamos ser capaces de construir un mostruo semejante que  pudiera sondear la distante energía de Planck (10¹⁹ GeV), pero sí podría habernos ofrecido una evidencia muy fuerte (aunque indirecta) de la corrección de la teoría de supercuerdas.

Este supercolisionador fue un proyecto fallido que se hubiese completado en las afueras de Dallas, Texas, hubiera contado con un tubo gigantesco de 85 Km de circunferencia rodeado de enormes bobinas magnéticas. Lanzaría protones a velocidades muy cercanas a la de la luz, que viajarían en el sentido de las agujas del reloj y el sentido contrario, para en un momento dado hacerlos colisionar a una energía de 40 billones de electronvoltios (TeV), generando una intensa ráfaga de residuos subatómicos analizados por detectores que encontrarían partículas exóticas que hubieran arrojado luz sobre la forma esencial de la materia. Los campos magnéticos para guiar los protones y los antiprotones dentro del tubo son tan excepcionalmente grandes (del orden de 100.000 veces el campo magnético de la Tierra) que hubieran sido necesarios procedimientos extraordinarios para generarlos y mantenerlos. Además, el enfriamiento de las bobinas hasta casi el cero absoluto (-273º) y otros problemas hubieran obligado a enormes avances tecnológicos. Sin embargo, la política retiró el proyecto y nos quedamos sin la esperada partícula de Higgs, que es la que genera la ruptura de simetría y es por tanto el origen de la masa de los quarks, así que habríamos podido descubrir el origen de la masa.

Me viene a la memoria que en el siglo XIX algunos científicos declararon que la composición de las estrellas estaría siempre fuera del alcance del experimento. En 1.825, el filósofo y crítico social francés Auguste Comte, al escribir el Curso de Filosofía, declaraba que nunca conoceríamos las estrellas de otra forma que como inalcanzables puntos de luz en el cielo debido a su enorme distancia de nosotros. Las máquinas del siglo XIX, o de cualquier siglo, argumentaba, no eran suficientemente potentes como para escapar de la Tierra y alcanzar las estrellas.

Así que parecía que el determinar la composición de las estrellas era imposible, y lo curioso es que casi al mismo tiempo, el físico alemán Joseph von Fraunhofer estuviera haciendo precisamente eso. Utilizando un prisma y un espectroscópio pudo descomponer la luz blanca emitida desde las estrellas lejanas y determinar la composición química de dichas estrellas. De la misma manera pudiera, en este mismo instante, estar trabajando un físico-matemático en profundizar en la teoría de supercuerdas y estar formulando otro respetable avance hacia nuestro futuro.

Como científico, ingeniero y emprendedor alcanzó logros como el descubrimiento de las “líneas de Fraunhofer” en el espectro óptico de la luz del sol, inventó un nuevo método de manufactura de lentes e inició un negocio de producción de vidrio para microscopios y telescopios. Debido a su carácter multifacético el instituto tecnológico Fraunhofer-Gesellschaft  lleva su apellido.

¿Qué sería de nosotros sin la física?

Tampoco los átomos eran verificables hace dos siglos y llegaron Planck, Einstein,  Bohr, Heisenberg, Schrödinger, Feyman y tantos otros que dejaron todo el misterio al descubierto con la mecánica cuántica que nos puede facilitar datos con una precisión asombrosa.

La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, ésto es, análisis de la posición. No podemos perderla de vista, ahí pueden estar las respuestas de la teoría de cuerdas.

Es la rama de las matemáticas  dedicada al estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas.¹ Es una disciplina que estudia las propiedades de los espacios topológicos y las funciones continuas.  La Topología se interesa por conceptos como proximidad, número de agujeros, el tipo deconsistencia (o textura) que presenta un objeto, comparar objetos y clasificar, entre otros múltiples atributos donde destacann conectividad, compacidad, metricidad, o metrizabilidad, etcétera.

Retrato de Leonhard Euler, pintado por Johann Georg Bruker

De todas las maneras, yo no perdería de vista la funciones modulares de Ramanujan, una bella teoría para la teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.

No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10, 11 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Los teóricos de cuerdas al intentar manipular los diagramas de lazos KSV ( Kikkawa-Sakita-Virasoro) creados por las cuerdas en interacción encuentran unas extrañas funciones llamadas modulares que aparecen en las ramas más distantes e “inconexas” de las matemáticas((Yutaka Taniyama ( Japón, 1927-1958) observó que cada función modular está relacionada con una curva elíptica. Esto forma la base de la conjetura Taniyama-Shimura que demostró ser una parte importante en la demostración del Último Teorema de Fermat de Andrew Wiles )). Una función que aparece continuamente en la teoría de funciones modulares se denomina función de Ramanujan, en honor al matemático Srinivasa Ramanujan, nacido en 1887 en Erode, India, cerca de Madrás.

Ramunujan ¡Qué personaje mistrioso! su mente estaba conformada por teoremas en lugar de por neuronas, y, aunque murió muy joven (como Riemann), sus trabajos del último año de su vida mientras se estaba muriendo, se podría comparar con el trabajo de toda una vida de los 10 mejores matemáticos del mundo. En otra ocasión ya os hablé de este personaje extensamente.

emilio silvera

[?]