Jul
31
¡La Luz! Esa maravilla
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Grandes pensadores quisieron explicar la naturaleza de la luz
Está claro que, los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.
Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

Siempre nos gustó hacer experimentos con la luz
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden.

Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro”, “fantasma”).

Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.
Le surgieron y se planteó algunas inquietudes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?


Titán, la luna de Saturno, contempla la sonda que lleva su nombre
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.
Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Peor la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sombras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿cuál era esa mecánica ondulatoria?
Interferencia: Sonido más sonido en algunos casos puede producir silencio. Esto sucede cuando dos ondas de sonido se superponen destructivamente, igual como se observa en las zonas nodales de una cuerda en vibración. ¿Será posible que en algún caso luz más luz produzca oscuridad? La respuesta es afirmativa. Quien lo demostrara en 1803, en un famoso experimento, fue Thomas Young (1773-1829). Éste consistió en hacer llegar un haz de luz simultáneamente a dos rendijas muy delgadas y muy cercanas, según se ilustra en el siguiente esquema.
Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular, de Newton, fue, con mucho, la más popular, en parte, porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico ingles, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos. Si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. Pero no fue esto lo que descubrió Young. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras. Pareció incluso que, en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.

Sería fácil explicarlo mediante la teoría ondulatoria. La banda luminosa representaba el refuerzo presado por las ondas de un rayo a las ondas del otro. Dicho de otra manera: Entraba “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.
Considerando la anchura de las bandas y la distancia entre los dos edificios por los que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. (Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Angströn. Esta unidad, denominada, en honor a su autor Ángstrom (Á), es la cienmillonésima parte de un centímetro. Así, pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Á, y la de la luz violeta, a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.)
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si éste no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior de una onda luminosa y, por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de la onda luminosa (por ejemplo, los virus y otras partículas submicroscópicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.

Augustin Jean Fresnel (1788 – 1827)
Photo: German Museum Munich
Un físico francés, Augustin-Jean Fresnel, fue quien demostró por vez primera, en 1.818, que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de disfracción” actúan como una serie de minúsculos obtáculos, que se refuerzan entre si. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso: los rayos espectrales. El físico americano Henry Augustus Rowlane ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.
Jacques Babinet
No sólo se aceptó las existencias de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalterable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento, denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuáles aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.

Tubo de descarga lleno de kriptón puro
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de longitud. Entonces se restableció la longitud de metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumento mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
Ahora, después de todo esto, sabemos algo más sobre la luz. Pero…, ¿qué pasa con su velocidad?
¡Veámoslo!

La velocidad de la luz, desde hace mucho tiempo, fue un misterio que los estudiosos de la física de la Naturaleza querían desvelar
Está claro que, la luz se desplaza a enormes velocidades. Si pulsamos el interruptor de apagado de la lámpara de nuestro salón, todo queda a oscuras de manera instantánea y, de la misma manera e inmediata, todo se inunda de luz si con una potente linterna encendida, apuntamos hacia un rincón oscuro.
La velocidad del sonido es más lenta, por ejemplo, si vemos a un leñador que está cortando leña en un lugar alejado de nosotros, sólo oiremos los golpes momentos después de que caiga el hacha. Así, pues, el sonido tarda cierto tiempo en llegar a nuestros oídos. En realidad es fácil medir la velocidad de su desplazamiento: unos 1.206 km/h en el aire y a nivel del mar.

Galileo fue el primero en intentar medir la velocidad de la luz. Se colocó en lo alto de una colina, mientras que su ayudante, se situaba en otro lugar alto de la colina vecina; luego sacó una linterna encendida: tan pronto como su ayudante vió la luz, hizo una señal con otra linterna. Galileo repitió el experimento a distancias cada vez mayores, suponiendo que el tiempo requerido por su ayudante para responder mantendría una uniformidad constante, por lo cual, el intervalo entre la señal de su propia linterna y la de su ayudante representaría el tiempo empleado por la luz para recorrer cada distancia. Aunque la idea era lógica, la luz viajaba demasiado aprisa como para que Galileo pudiera percibir las sutiles diferencias con un método tan rudimentario.

En 1.676, el astrónomo danés Olau Roemer logró cronometrar la velocidad de la luz a escala de distancias astronómicas. Estudiando los eclipses de Júpiter en sus cuatro grandes satélites, Roemer observó que el intervalo entre eclipses consecutivos era más largo cuando la Tierra se alejaba de Júpiter, y más corto cuado se movía en su órbita hacía dicho astro. Al parecer, la diferencia entre las duraciones del eclipse reflejaba la diferencia de distancias entre la Tierra y Júpiter. Y trataba, pues, de medir la distancia partiendo del tiempo empleado por la luz para trasladarse desde Júpiter hasta la Tierra. Calculando aproximadamente el tamaño de la órbita terrestre y observando la máxima discrepancia en las duraciones del eclipse que, según Roemer, representaba el tiempo que necesitaba la luz para atravesar el eje de al órbita terrestre, dicho astrónomo computó la velocidad de la luz. Su resultado, de 225.000 km/s., parece excelente si se considera que fue el primer intento, y resultó bastante asombroso como para provocar la incredulidad de sus coetáneos.
Sin embargo, medio siglo después se confirmaron los cálculos de Roemer en un campo totalmente distinto. Allá por 1.728, el astrónomo británico James Bradley descubrió que las estrellas parecían cambiar de posición con los movimientos terrestres; y no por el paralaje, sino porque la traslación terrestre alrededor del Sol era una fracción mensurable (aunque pequeña) de la velocidad de la luz. La analogía empleada usualmente es la de un hombre que camina con el paraguas abierto bajo un temporal. Aun cuando las gotas caigan verticalmente, el hombre debe inclinar hacia delante el paraguas, porque ha de abrirse paso entre las gotas.

James Bradley descubrió la aberración estelar
Cuanto más acelere su paso, tanto más deberá inclinar el paraguas. De manera semejante la Tierra avanza entre los ligeros rayos que caen desde las estrellas, y el astrónomo debe inclinar un poco su telescopio y hacerlo en varias direcciones, de acuerdo con los cambios de la trayectoria terrestre (no olvidemos que nuestro planeta Tierra, es como una enorme nave espacial que nos lleva en un viaje eterno, alrededor del Sol, a la velocidad de 30 km/s. + -) Mediante ese desvío aparente de los astros (“aberración de la luz”), Bradley pudo evaluar la velocidad de la luz y calcularla con gran precisión.
Sus cálculos fueron de 285.000 km/s, bastante más exacto que los de Roemer, pero aún un 5’5% más bajos. Poco a poco, con medios tecnológicos más sofisticados y más conocimientos matemáticos, los científicos fueron obteniendo medidas más exactas aún, conforme se fue perfeccionando la idea original de Galileo y sus sucesores.
En 1.849, el físico francés Armand-Hippolyte-Louis Fizeau ideó un artificio mediante el cual se proyectaba la luz sobre un espejo situado a 8 km de distancia, que devolvía el reflejo al observador. El tiempo empleado por la luz en su viaje de ida y vuelta no rebasó apenas la 1/20.000 de segundo, por Fizeau logró medirlo colocando una rueda dentada giratoria en la trayectoria del rayo luminoso. Cuando dicha rueda giraba a cierta velocidad, regulada, la luz pasaba entre los dientes y se proyectaba contra el siguiente, al ser devuelta por el espejo; así, Fizeau, colocado tras la rueda, no pudo verla. Entonces se dio más velocidad a la rueda, y el reflejo pasó por la siguiente muesca entre los dientes, sin intercepción alguna. De esa forma, regulando y midiendo la velocidad de la rueda giratoria, Fizeau pudo calcular el tiempo transcurrido y, por consiguiente, la velocidad a que se movía el rayo de luz.
Un año más tarde, Jean Foucault (quien realizaría poco después su experimento con los péndulos) precisó más estas medidas empleando un espejo giratorio en ve de una rueda dentada. Entonces se midió el tiempo transcurrido desviando ligeramente el ángulo de reflexión mediante el veloz espejo giratorio. Foucault obtuvo un valor de la velocidad de la luz de 300.883 km/s. También, el físico francés utilizó su método para determinar la velocidad de la luz a través de varios líquidos. Averiguó que era notablemente inferior a la alcanzada en el aire. Esto concordaba también con la teoría ondulatoria de Huyghens.

Michelson fue más preciso aún en sus medidas. Este autor, durante cuarenta años largos, a partir de 1.879, fue aplicando el sistema Fizeau-Foucault cada vez con mayor refinamiento, para medir la velocidad de la luz. Cuando se creyó lo suficientemente informado, proyectó la luz a través de vacío, en vez de hacerlo a través del aire, pues este frena ligeramente su velocidad, y, empleó para ello tuberías de acero cuya longitud era superior a 1’5 km. Según sus medidas, la velocidad de la luz en el vacío era de 299.730 km(seg. (sólo un 0’006% más bajo). Demostraría también que todas las longitudes de ondas luminosas viajan a la misma velocidad en el vacío.
En 1.972, un equipo de investigadores bajo la dirección de Kenneth M. Eveson efectuó unas mediciones aún más exactas y vio que la velocidad de la luz era de 299.727’74 km/seg. Una vez se conoció la velocidad de la luz con semejante precisión, se hizo posible usar la luz, o por lo menos formas de ella, para medir distancias.
Aunque para algunos resulte alto tedioso el tema anterior, no he podido resistirme a la tentación de exponerlo, así podrá saber algo más sobre la luz y, habrán conocido a personajes que hicieron posible el que ahora nosotros, la conozcamos mejor.

Podría continuar, hasta el final de este trabajo, hablando de la luz y sus distintas formas o aplicaciones: ondas de luz a través del espacio, de cómo se transmite la luz en el “vacío”, nos llega a través del espacio desde Galaxias situadas a miles de millones de años luz; las líneas de fuerzas electromagnéticas de Faraday y Maxwell de campos eléctricos y magnéticos cambiantes (todo ello explicado en un simple conjunto de cuatro ecuaciones, que describían casi todos los fenómenos referentes a esta materia electromagnética), o de los enigmas aún por descubrir (aunque predichos).
Ahora, en Física, se dice que la luz es una forma de radiación electromagnética a la que el ojo humano es sensible y sobre la cual depende nuestra consciencia visual del universo y sus contenidos.

Aparte de todo lo que antes hemos explicado, no sería justo finalizar el trabajo sin exponer aquí que, en 1905, Albert Einstein, inspirado en el cuanto de Planck, realizó un importante avance en el conocimiento de lo que es la luz. Demostró que el Efecto fotoeléstrico sólo podía ser explicado con la hipótesis de que la luz consiste en un chorro de fotones de energía electromagnética discretos. Aquello le valió el Nobel de Física y… ¡Le hurtaron otros dos por las dos partes de su teoría de la relatividad! Una revolución que lo cambió todo y que nunca podremos pagarle.
El conflicto entre la teoría ondulatoria y corpuscular de la luz fue resuelto con la evolución de la teoría cuántica y la mecánica ondulatoria que ha dejado claro que, los electrones y las otras partículas elementales tienen propiedades duales de partículas y onda.
sería mucho más largo, pero creo que está bien con lo dicho.
emilio silvera
Jul
30
¡Conocer la Naturaleza! Hoy sólo un sueño ¿Realidad mañana?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo de Ayar y el Universo de Hoy ~
Clasificado en El Universo de Ayar y el Universo de Hoy ~
 Comments (0)
Comments (0)

A partir de sus principios en Sumeria (actualmente en Irak) alrededor del 3500 a. C., en Mesopotamia, los pueblos del norte comenzaron a intentar registrar la observación del mundo con datos cuantitativos y numéricos sumamente cuidados. Pero sus observaciones y medidas aparentemente fueron tomadas con otros propósitos más que la ley científica. Un caso concreto es el del teorema de Pitágoras, que fue registrado, aparentemente en el siglo XVIII a. C.: la tabla mesopotámica Plimpton 322 registra un número de trillizos pitagóricos (3,4,5) (5,12,13)…., datado en el 1900 a. C., posiblemente milenios antes de Pitágoras,1 pero no era una formulación abstracta del teorema de Pitágoras.
Los avances significativos en el Antiguo Egipto son referentes a la astronomía, a las matemáticas y a la medicina.2 Su geometría era una consecuencia necesaria de la topografía, con el fin de intentar conservar la disposición y la propiedad de las tierras de labranza, que fueron inundadas cada año por el Nilo. La regla del triángulo rectángulo y otras reglas básicas sirvieron para representar estructuras rectilíneas, el pilar principal de la arquitectura dintelada egipcia. Egipto era también el centro de la química y la investigación para la mayor parte del Mediterráneo.

Isabel Pérez Arellano y Róbinson Torres Villa, publicaron un artículo en 2009, sobre la física moderna y sus paradigmas y, comenzaban diciendo:
“Desde siempre el hombre ha intentado dar respuesta a los interrogantes más profundos que lo inquietan; preguntas
que van desde ¿Quién soy?, ¿de dónde vengo? ¿y hacia dónde voy?, hasta los intentos por explicar el origen y final universo en qué vive. Muchas son las prepuestas que se han dado a esos interrogantes, dependiendo de la corriente de pensamiento seguida por quien aborda esas preguntas; es así como se ven aproximaciones místicas, esotéricas, religiosas y científicas entre otras; pero todas con el objetivo de dilucidar alguna respuesta a esas preguntas fundamentales.
Desde el punto de vista científico y concretamente de la física moderna, se han planteado algunas explicaciones del universo en el que vivimos que algunas veces rozan con lo fantástico, dado el nivel de abstracción o especulación que llevan implícito, todo obviamente avalado por sofisticados modelos matemáticos que al parecer soportan las hipótesis planteadas.”
Si repasamos la historia de la ciencia, seguramente encontraremos muchos motivos para el optimismo. Por mencionar a un científico de nuestro tiempo, escojamos a E. Witten que está convencido de que la ciencia será algún día capaz de sondear hasta las energías de Planck. Como ya he contado en otras ocasiones, él dijo:
“No siempre es tan fácil decir cuáles son las preguntas fáciles y cuáles las difíciles. En el siglo XIX, la pregunta de por qué el agua hierve a 100 grados era desesperadamente inaccesible. Si usted hubiera dicho a un físico del siglo XIX que hacia el siglo XX sería capaz de calcularlo, le habría parecido un cuento de hadas… La teoría cuántica de campos es tan difícil que nadie la creyó completamente durante 25 años.”
En su opinión, las buenas ideas siempre se verifican. Los ejemplos son innumerables: la gravedad de Newton, el campo eléctrico de Faraday y el electromagnetismo de Maxwell, la teoría de la relatividad de Einstein en sus dos versiones y su demostración del efecto fotoeléctrico, la teoría del electrón de Paul Dirac, el principio de incertidumbre de Heisenberg, la función de ondas de Schrödinger, y tantos otros. Algunos de los físicos teóricos más famosos, sin embargo, protestaban de tanto empeño en la experimentación.

El astrónomo arthur Eddington se cuestionaba incluso si los científicos no estaban forzando las cosas cuando insistían en que todo debería ser verificado. El premio Nobel Paul dirac incluso llegó a decir de forma más categórica: “Es más importante tener belleza en las ecuaciones que tener experimentos que se ajusten a ellas“, o en palabras del físico John Ellis del CERN, “Como decía en una envoltura de caramelos que abrí hace algunos años, «Es sólo el optimista el que consigue algo en este mundo».“
Yo, como todos ustedes, un hombre normal y corriente de la calle, escucho a unos y a otros, después pienso en lo que dicen y en los argumentos y motivaciones que les han llevado a sus respectivos convencimientos, y finalmente, también decido según mis propios criterios y emito mi opinión de cómo es el mundo que, no obligatoriamente, coincidirá con alguna de esas opiniones, y que en algún caso, hasta difieren radicalmente.

Suponiendo que algún físico brillante nos resuelva la teoría de campos de cuerdas y derive las propiedades conocidas de nuestro universo, con un poco de suerte, podría ocurrir en este mismo siglo, lo que no estaría nada mal considerando las dificultades de la empresa. El problema fundamental es que estamos obligando a la teoría de supercuerdas a responder preguntas sobre energías cotidianas, cuando su “ámbito natural” está en la energía de Planck. Esta fabulosa energía fue liberada sólo en el propio instante de la creación, lo que quiere decir que la teoría de supercuerdas tiene su explicación allí, en aquel lugar y tiempo donde se produjeron las mayores energías conocidas en nuestro Universo y que, nosotros, no podemos alcanzar -de momento-.
Fuimos capaces de predecir que el Big Bang produjo un “eco” cósmico reverberando en el universo y que podría ser mesurable por los instrumentos adecuados. De hecho, Arno Penzias y Robert Wilson de los Bell Telephone Laboratories ganaron el premio Nobel en 1.978 por detectar este eco del Big Bang, una radiación de microondas que impregna el universo conocido.

Como una onda, podemos detectar el eco del big bang
El que el eco del Big Bang debería estar circulando por el universo miles de millones de años después del suceso fue predicho por primera vez por George Gamow y sus discípulos Ralpher y Robert Herman, pero nadie les tomó en serio. La propia idea de medir el eco de la creación parecía extravagante cuando la propusieron por primera vez poco después de la segunda guerra mundial. Su lógica, sin embargo, era aplastante. Cualquier objeto, cuando se calienta, emite radiación de forma gradual. Ésta es la razón de que el hierro se ponga al rojo vivo cuando se calienta en un horno, y cuanto más se calienta, mayor es la frecuencia de radiación que emite. Una fórmula matemática exacta, la ley de Stefan-Boltzmann, relaciona la frecuencia de la luz (o el color en este caso) con la temperatura. De hecho, así es como los científicos determinan la temperatura de la superficie de una estrella lejana; examinando su color. Esta radiación se denomina radiación de cuerpo negro.

Esta radiación, ¡cómo no!, ha sido aprovechada por los ejércitos, que mediante visores nocturnos pueden operar en la oscuridad. De noche, los objetos relativamente calientes, tales como soldados enemigos o los carros de combate, pueden estar ocultos en la oscuridad, pero continúan emitiendo radiación de cuerpo negro invisible en forma de radiación infrarroja, que puede ser captada por gafas especiales de infrarrojo. Ésta es también la razón de que nuestros automóviles cerrados se calientes en verano, ya que la luz del Sol atraviesa los cristales del coche y calienta el interior. A medida que se calienta, empieza a emitir radiación de cuerpo negro en forma de radiación infrarroja. Sin embargo, esta clase de radiación no atraviesa muy bien el vidrio, y por lo tanto queda atrapada en el interior del automóvil, incrementando espectacularmente la temperatura y, cuando regresamos para proseguir el camino… ¿quién es el guapo que entra?


Análogamente, la radiación de cuerpo negro produce el efecto invernadero. Al igual que el vidrio, los altos niveles de dióxido de carbono en la atmósfera, causados por la combustión sin control de combustibles fósiles, pueden atrapar la radiación de cuerpo negro infrarroja en la Tierra, y de
este modo calentar gradualmente el planeta.
Gamow razonó que el Big Bang era inicialmente muy caliente, y que por lo tanto sería un cuerpo negro ideal emisor de radiación. Aunque la tecnología de los años cuarenta era demasiado primitiva para captar esta débil señal de la creación, Gamow pudo calcular la temperatura de dicha radiación y predecir con fiabilidad que un día nuestros instrumentos serían lo suficientemente sensibles como para detectar esta radiación “fósil”.
La lógica que había detrás de su razonamiento era la siguiente: alrededor de 300.000 años después del Big Bang, el universo se enfrió hasta el punto en el que los átomos pudieron empezar a componerse; los electrones, entonces, pudieron empezar a rodear a los protones y neutrones formando átomos estables, que ya no serían destruidos por la intensa radiación que estaba impregnando todo el universo. Antes de este momento, el universo estaba tan caliente que los átomos eran inmediatamente descompuestos por esa radiación tan potente en el mismo acto de su formación. Esto significa que el universo era opaco, como una niebla espesa absorbente e impenetrable.
Pasados 300.000 años, la radiación no era tan potente; se había enfriado y por lo tanto la luz podía atravesar grades distancias sin ser dispersada. En otras palabras, el universo se hizo repentinamente negro y transparente.

Terminaré esta parte comentando que un auténtico cuerpo negro es un concepto imaginario; un pequeño agujero en la pared de un recinto a temperatura uniforme es la mejor aproximación que se puede tener de él en la práctica. La radiación de cuerpo negro es la radiación electromagnética emitida por un cuerpo negro. Se extiende sobre todo el rango de longitudes de onda y la disminución de energías sobre este rango tiene una forma característica con un máximo en una cierta longitud de onda, desplazándose a longitudes de onda más cortas al aumentar las temperaturas*.
Hablar, sin más especificaciones, de radiación, es estar refiriéndonos a una energía que viaja en forma de ondas electromagnéticas o fotones por el universo. También nos podríamos estar refiriendo a un chorro de partículas, especialmente partículas alfa o beta de una fuente radiactiva o neutrones de un reactor nuclear.

Radiación y magnetismo presentes en todas partes
La radiación actínida es la electromagnética que es capaz de iniciar una reacción química. El término es usado especialmente para la radiación ultravioleta que emiten las estrellas jóvenes y azuladas en las bellas nebulosas.

Muchos son los tipos conocidos: Radiación blanda, radiación cósmica, radiación de calor, radiación de fondo, de fondo de microondas, radiación dura, electromagnética, radiación gamma, infrarroja, ionizante, monocromática, policromática, de sincrotón, ultravioleta, de la teoría cuántica, de radiactividad… y, como se puede ver, la radiación en sus diversas formas es un universo en sí misma.
El físico alemán Max Planck (1.858 – 1.947), responsable entre otros muchos logros de la ley de radiación de Planck, que da la distribución de energía radiada por un cuerpo negro. Introdujo en física el concepto novedoso de que la energía es una cantidad que es radiada por un cuerpo en pequeños paquetes discretos, en vez de una emisión continua. Estos pequeños paquetes se conocieron como cuantos y la ley formulada es la base de la teoría cuántica.
Einstein se inspiró en este trabajo para a su vez presentar el suyo propio sobre el efecto fotoeléctrico, donde la energía máxima cinética del fotoelectrón, Em, está dada por la ecuación que lleva su nombre: Em = hf – Φ.

Planck publicó en 1.900 un artículo sobre la radiación de cuerpo negro que sentó las bases para la teoría de la mecánica cuántica que más tarde desarrollaron otros, como el mismo Einstein, Heisenberg, Schrödinger, Dirac, Feymann, etc. Todos los físicos son conocedores de la enorme contribución que Max Planck hizo en física: la constante de Planck, radiación de Planck, longitud de Planck, unidades de Planck, etc. Es posible que sea el físico de la historia que más veces ha dado su nombre a conceptos de física. Pongamos un par te ejemplos de su ingenio:
1. Esta escala de longitud ( 10-35 m ) veinte órdenes de magnitud menor que el tamaño del protón, de 10-15 m, es a la que la descripción clásica de gravedad cesa de ser válida y debe ser tenida en cuenta la mecánica cuántica. En la fórmula que la describe, G es la constante gravitacional, ħ es la constante de Planck racionalizada y c en la velocidad de la luz.
2. Es la masa de una partícula cuya longitud de onda Compton es igual a la longitud de Planck. En la ecuación, ħ es la constante de Planck racionalizada, c es la velocidad de la luz y G es la constante gravitacional.
La descripción de una partícula elemental de esta masa, o partículas que interaccionan con energías por partículas equivalentes a ellas (a través de E = mc2), requiere de una teoría cuántica de la gravedad. Como la masa de Planck es del orden de 10-8 Kg (equivalente a una energía de 1019 GeV) y, por ejemplo, la masa del protón es del orden de 10-27 Kg y las mayores energías alcanzables en los aceleradores de partículas actuales son del orden de 14 TeV, los efectos de gravitación cuántica no aparecen en los laboratorios de física de partículas.

Únicamente en un laboratorio aparecieron partículas que tenían energías del orden de la masa de Planck: en el universo primitivo, de acuerdo con la teoría del Big Bang, motivo éste por el que es necesaria una teoría cuántica de la gravedad para estudiar aquellas condiciones. Esta energía de la que estamos hablando, del orden de 1019 GeV (inalcanzable para nosotros), es la que necesitamos para verificar la teoría de supercuerdas.
Siempre, desde que puedo recordar, me llamó la atención los misterios y secretos encerrados en la naturaleza, y la innegable batalla mantenida a lo largo de la historia por los científicos para descubrirlos.
emilio silvera
Jul
29
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física-química ~
Clasificado en Física-química ~
 Comments (0)
Comments (0)
Poco tiempo después resultó evidente que existían otras subpartículas en el interior del átomo. Cuando Becquerel descubrió la radiactividad, identificó como emanaciones constituidas por electrones algunas de las radiaciones emitidas por sustancias radiactivas. Pero también quedaron al descubierto otras emisiones. Los Curie en Francia y Ernest Rutherford en Inglaterra detectaron una emisión bastante menos penetrante que el flujo electrónico. Rutherford la llamó rayos alfa, y denominó rayos beta a la emisión de electrones.
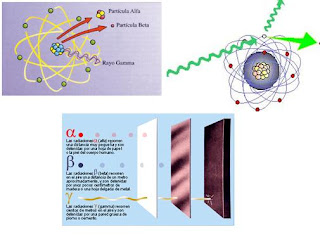
Los electrones volantes constitutivos de esta última radiación son, individualmente, partículas beta. Así mismo, se descubrió que los rayos alfa estaban formados por partículas, que fueron llamadas partículas alfa. Como ya sabemos, alfa y beta son las primeras letras del alfabeto griego y se escriben con los gráficos α y β.

Entretanto, el químico francés Paul Ulrico Villard descubría una tercera forma de emisión radiactiva, a la que dio el nombre de rayos gamma, es decir, la tercera letra del alfabeto griego (γ). Pronto se identificó como una radiación análoga a los rayos X, aunque de menor longitud de onda.
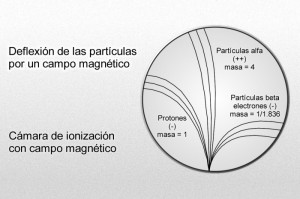
Mediante sus experimentos, Rutherford comprobó que un campo magnético desviaba las partículas alfa con mucho menos fuerza que las partículas beta. Por añadidura, las desviaba en dirección opuesta, lo cual significaba que la partícula alfa tenía una carga positiva, es decir, contraria a la negativa del electrón. La intensidad de tal desviación permitió calcular que la partícula alfa tenía como mínimo una masa dos veces mayor que la del hidrogenión, cuya carga positiva era la más pequeña conocida hasta entonces.

En 1.909, Rutherford pudo aislar las partículas alfa. Puso material radiactivo en un tubo de vidrio fino rodeado por vidrio grueso, e hizo el vacío entre ambas superficies. Las partículas alfa pudieron atravesar la pared fina, pero no la gruesa, lo que dio lugar a que las partículas quedaran aprisionadas entre ambas, y Rutherford recurrió entonces a la descarga eléctrica para excitar las partículas alfa, hasta llevarlas a la incandescencia. Entonces mostraron los rayos espectrales del helio.

Hay pruebas de que laspartículas alfa producidas por sustancias radiactivas en el suelo constituyen el origen del helio en los pozos de gas natural. Si la partícula alfa es helio, su masa debe ser cuatro veces mayor que la del hidrógeno. Ello significa que la carga positiva de éste último equivale a dos unidades, tomando como unidad la carga del hidrogenión.
Más tarde, Rutherford identificó otra partícula positiva en el átomo. A decir verdad, había sido detectada y reconocida ya muchos años antes. En 1.886, el físico alemán Eugen Goldstein, empleando un tubo catódico con un cátodo perforado, descubrió una nueva radiación que fluía por los orificios del cátodo en dirección opuesta a la de los rayos catódicos. La denominó rayos canales.

Part of Astronomy that study physical and chemical characteristics of heavenly bodies. Astrophysics is the most important part of Astronomy at the present time owing to advance of modern physics. Doppler- Fizeau´s effect, Zeeman´s effect, quantum theories and thermonuclear reactions applied to study of heavenly bodies have permitted to discover the solar magnetic field, study stellar radiations and their processes of nuclear fusion, and determine radial velocity of stars, etc. Electromagnetic radiation of heavenly bodies permits to make spectrum analysis of themselves, and they are the principal fountain of information in this part of Astronomy
En 1.902, esta radiación sirvió para detectar por vez primera el efecto Doppler-Fizeau respecto a las ondas luminosas de origen terrestre. El físico alemán de nombre Johannes Stara orientó un espectroscopio de tal forma que los rayos cayeron sobre éste, revelando la desviación hacia el violeta. Por estos trabajos se le otorgó el premio Nobel de Física en 1.919.
Puesto que los rayos canales se mueven en dirección opuesta a los rayos catódicos de carga negativa, Thomson propuso que se diera a esta radiación el nombre de rayos positivos. Entonces se comprobó que las partículas de rayos positivos podían atravesar fácilmente la materia. De aquí que fuesen considerados, por su volumen, mucho más pequeños que los iones corrientes o átomos. La desviación determinada, en su caso, por un campo magnético, puso de relieve que la más ínfima de estas partículas tenía carga y masa similares a los del hidrogenión, suponiendo que este ión contuviese la misma unidad posible de carga positiva.
Por consiguiente se dedujo que la partícula del rayo positivo era la partícula positiva elemental, o sea, el elemento contrapuesto al electrón; Rutherford lo llamó protón (del neutro griego proton, “lo primero”).
Desde luego, el protón y el electrón llevan cargas eléctricas iguales, aunque opuestas; ahora bien, la masa del protón, referida al electrón, es 1.836 veces mayor (como señalo en el gráfico anterior).
Parecía probable pues que el átomo estuviese compuesto por protones y electrones, cuyas cargas se equilibraran entre sí. También parecía claro que los protones se hallaban en el interior del átomo y no se desprendían, como ocurría fácilmente con los electrones. Pero entonces se planteó el gran interrogante: ¿cuál era la estructura de esas partículas en el átomo?
El núcleo atómico

El propio Rutherford empezó a vislumbrar la respuesta. Entre 1.906 y 1.908 (hace ahora un siglo) realizó constantes experimentos disparando partículas alfa contra una lámina sutil de metal (como oro o platino), para analizar sus átomos. La mayor parte de los proyectiles atravesaron la barrera sin desviarse (como balas a través de las hojas de un árbol), pero no todos. En la placa fotográfica que le sirvió de blanco tras el metal, Rutherford descubrió varios impactos dispersos e insospechados alrededor del punto central. Comprobó que algunas partículas habían rebotado. Era como si en vez de atravesar las hojas, algunos proyectiles hubiesen chocado contra algo más sólido. Rutherford supuso que aquella “balas” habían chocado contra una especie de núcleo denso, que ocupaba sólo una parte mínima del volumen atómico y ese núcleo de intensa densidad desviaban los proyectiles que acertaban a chocar contra él. Ello ocurría en muy raras ocasiones, lo cual demostraba que los núcleos atómicos debían ser realmente ínfimos, porque un proyectil había de encontrar por fuerza muchos millones de átomos al atravesar la lámina metálica.
Era lógico suponer, pues, que los protones constituían ese núcleo duro. Rutherford representó los protones atómicos como elementos apiñados alrededor de un minúsculo “núcleo atómico” que servía de centro (después de todo eso, hemos podido saber que el diámetro de ese núcleo equivale a algo más de una cienmilésima del volumen total del átomo).
En 1.908 se concedió a Rutherford el premio Nobel de Química por su extraordinaria labor de investigación sobre la naturaleza de la materia. Él fue el responsable de importantes descubrimientos que permitieron conocer la estructura de los átomos en esa primera avanzadilla.

Desde entonces se pueden describir con términos más concretos los átomos específicos y sus diversos comportamientos. Por ejemplo, el átomo de hidrógeno posee un solo electrón. Si se elimina, el protón restante se asocia inmediatamente a alguna molécula vecina; y cuando el núcleo desnudo de hidrógeno no encuentra por este medio un electrón que participe, actúa como un protón (es decir, una partícula subatómica), lo cual le permite penetrar en la materia y reaccionar con otros núcleos si conserva la suficiente energía.
El helio, que posee dos electrones, no cede uno con tanta facilidad. Sus dos electrones forman un caparazón hermético, por lo cual el átomo es inerte. No obstante, si se despoja al helio de ambos electrones, se convierte en una partícula alfa, es decir, una partícula subatómica portadora de dos unidades de carga positiva.

Con tres electrones, el litio es el elemento sólido más ligero
Hay un tercer elemento, el litio, cuyo átomo tiene tres electrones. Si se despoja de uno o dos, se transforma en ión, y si pierde los tres, queda reducida a un núcleo desnudo, con una carga positiva de tres unidades.
Las unidades de carga positiva en el núcleo atómico deben ser numéricamente idénticas a los electrones que contiene por norma, pues el átomo suele ser un cuerpo neutro, y esta igualdad de lo positivo con lo negativo es el equilibrio. De hecho, los números atómicos de sus elementos se basan en sus unidades de carga positiva, no en las de carga negativa, porque resulta fácil hacer variar el número de electrones atómicos dentro de la formación iónica, pero en cambio se encuentran grandes dificultades si se desea alterar el número de sus protones.
Apenas esbozado este esquema de la construcción atómica, surgieron nuevos enigmas. El número de unidades con carga positiva en un núcleo no equilibró, en ningún caso, el peso nuclear ni la masa, exceptuando el caso del átomo de hidrógeno. Para citar un ejemplo, se averiguó que el núcleo de helio tenía una carga positiva dos veces mayor que la del núcleo de hidrógeno; pero como ya se sabía, su masa era cuatro veces mayor que la de este último. Y la situación empeoró progresivamente a medida que se descendía por la tabla de elementos, e incluso cuando se alcanzó el uranio, se encontró un núcleo con una masa igual a 238 protones, pero una carga que equivalía sólo a 92.

¿Cómo era posible que un núcleo que contenía cuatro protones (según se suponía el núcleo de helio) tuviera sólo dos unidades de carga positiva? Según la más simple y primera conjetura emitida, la presencia en el núcleo de partículas cargadas negativamente y con peso despreciable neutralizaba dos unidades de carga. Como es natural, se pensó también en el electrón. Se podría componer el rompecabezas si se suponía que en núcleo de helio estaba integrado por cuatro protones y dos electrones neutralizadores, lo cual deja libre una carga positiva neta de dos, y así sucesivamente, hasta llegar al uranio, cuyo núcleo tendría, pues, 238 protones y 146 electrones, con 92 unidades libres de carga positiva. El hecho de que los núcleos radiactivos emitieran electrones (según se había comprobado ya, por ejemplo, en el caso de las partículas beta), reforzó esta idea general. Dicha teoría prevaleció durante más de una década, hasta que por caminos indirectos, llegó una respuesta mejor como resultado de otras investigaciones.

Pero entre tanto se habían presentado algunas objeciones rigurosas contra dicha hipótesis. Por lo pronto, si el núcleo estaba constituido esencialmente de protones, mientras que los ligeros electrones no aportaban prácticamente ninguna contribución a la masa, ¿cómo se explicaba que las masas relativas de varios núcleos no estuvieran representadas por número enteros? Según los pesos atómicos conocidos, el núcleo del átomo cloro, por ejemplo, tenía una masa 35’5 veces mayor que la del núcleo de hidrógeno. ¿Acaso significaba esto que contenía 35’5 protones? Ningún científico (ni entonces ni ahora) podía aceptar la existencia de medio protón.
Este singular interrogante encontró una respuesta incluso antes de solventar el problema principal, y ello dio lugar a una interesante historia.
Isótopos; construcción de bloques uniforme,
Allá por 1.816, el físico inglés William Prout había insinuado ya que el átomo de hidrógeno debía entrar en la constitución de todos los átomos. Con el tiempo se fueron desvelando los pesos atómicos, y la teoría de Prout quedó arrinconada, pues se comprobó que muchos elementos tenían pesos fraccionarios (para lo cual se tomó el oxígeno, tipificado al 16). El cloro, según dije antes, tiene un peso atómico aproximado de 35’5, o para ser exactos, 35’457. otros ejemplos son el antimonio, con un peso atómico de 121’75, el galio con 137’34, el boro con 10’811 y el cadmio con 112’40.

Hacia principios de siglo se hizo una serie de observaciones desconcertantes, que condujeron al esclarecimiento. El inglés William Crookes (el del tubo Crookes) logró disociar del uranio una sustancia cuya ínfima cantidad resultó ser mucho más radiactiva que el propio uranio. Apoyándose en su experimento, afirmó que el uranio no tenía radiactividad, y que ésta procedía exclusivamente de dicha impureza, que él denominó uranio X. Por otra parte, Henri Becquerel descubrió que el uranio purificado y ligeramente radiactivo adquiría mayor radiactividad con el tiempo, por causas desconocidas. Si se deja reposar durante algún tiempo, se podía extraer de él repetidas veces uranio activo X. Para decirlo de otra manera, por su propia radiactividad, el uranio se convertía en el uranio X, más radiactivo aún.
Por entonces, Rutherford, a su vez, separó del torio un torio X muy radiactivo, y comprobó también que el torio seguía produciendo más torio X. Hacia aquellas fechas se sabía ya que el más famoso de los elementos radiactivos, el radio, emitía un gas radiactivo, denominado radón. Por tanto, Rutherford y su ayudante, el químico Frederick Soddy, dedujeron que durante la emisión de sus partículas los átomos radiactivos se transformaron en otras variedades de átomos radiactivos.
El material radiactivo llega a producir mutaciones.
Varios químicos que investigaron tales transformaciones lograron obtener un surtido muy variado de nuevas sustancias, a las que dieron nombres tales como radio A, radio B, mesotorio I, mesotorio II y actinio C. Luego los agruparon todos en tres series, de acuerdo con sus historiales atómicos. Una serie se originó del uranio disociado; otra del torio, y la tercera del actinio (si bien más tarde se encontró un predecesor del actinio, llamado protactinio).
En total se identificaron unos cuarenta miembros de esas series, y cada uno se distinguió por su peculiar esquema de radiación. Pero los productos finales de las tres series fueron idénticos: en último término, todas las cadenas de sustancias conducían al mismo elemento, el plomo.
Ahora bien, esas cuarenta sustancias no podían ser, sin excepción, elementos disociados. Entre el uranio (92) y el plomo (82) había sólo diez lugares en la tabla periódica, y todos ellos, salvo dos, pertenecían a elementos conocidos.
Hay que huir de los desechos radiactivos que causan la actividad del hombre
En realidad, los químicos descubrieron que aunque las sustancias diferían entre sí por su radiactividad, algunas tenían propiedades químicas idénticas. Por ejemplo, ya en 1.907 los químicos americanos Herbert Newby McCoy y W. H. Ross descubrieron que el radiotorio (uno entre los varios productos de la desintegración del torio) mostraba el mismo comportamiento químico que el torio, y el radio D, el mismo que el plomo, tanto que a veces era llamado radioplomo. De todo lo cual se infirió que tales sustancias eran en realidad variedades de mismo elemento: el radiotorio, una forma de torio; el radioplomo, un miembro de una familia de plomos; y así sucesivamente.
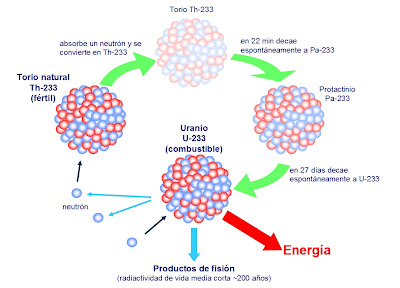
En 1.913, Soddy esclareció esta idea y le dio más amplitud. Demostró que cuando un átomo emitía una partícula alfa, se transformaba en un elemento que ocupaba dos lugares más abajo en la lista de elementos, y que cuando emitía una partícula beta, ocupaba, después de su transformación, el lugar inmediatamente superior. Con arreglo a tal norma, el radiotorio descendía en la tabla hasta el lugar del torio, y lo mismo ocurría con las sustancias denominadas uranio X y uranio Y, es decir, que los tres serían variedades del elemento 90. Así mismo, el radio D, el radio B, el torio B y el actinio B compartirían el lugar del plomo como variedades del elemento 82.

Soddy dio el nombre de isótopos (del griego iso y topos, “el mismo lugar”) a todos los miembros de una familia de sustancias que ocupaban el mismo lugar en la tabla periódica. En 1.921 se le concedió el premio Nobel de Química.
El modelo protón–electrón del núcleo concordó perfectamente con la teoría de Soddy sobre los isótopos. Al retirar una partícula alfa de un núcleo, se reducía en dos unidades la carga positiva de dicho núcleo, exactamente lo que necesitaba para bajar dos lugares en la tabla periódica. Por otra parte, cuando el núcleo expulsaba un electrón (partícula beta), quedaba sin neutralizar un protón adicional, y ello incrementaba en una unidad la carga positiva del núcleo, lo cual era como agregar una unidad al número atómico, y por tanto, el elemento pasaba a ocupar la posición inmediatamente superior en la tabla periódica de los elementos. ¡Maravilloso!

¿Cómo se explica que cuando el torio se descompone en radiotorio después de sufrir no una, sino tres desintegraciones, el producto siga siendo torio? Pues bien, en este proceso el átomo de torio pierde una partícula alfa, luego una partícula beta, y más tarde una segunda partícula beta. Si aceptamos la teoría sobre el bloque constitutivo de los protones, ello significa que el átomo ha perdido cuatro electrones (dos de ellos contenidos presuntamente en la partícula alfa) y cuatro protones. (La situación actual difiere bastante de este cuadro, aunque en cierto modo, esto no afecta al resultado).
El núcleo de torio constaba inicialmente (según se suponía) de 232 protones y 142 electrones. Al haber perdido cuatro protones y otros cuatro electrones, quedaba reducido a 228 protones y 138 electrones. No obstante, conservaba todavía el número atómico 90, es decir, el mismo de antes.

El torio en estado natural
Así pues, el radiotorio, a semejanza del torio, posee 90 electrones planetarios, que giran alrededor del núcleo. Puesto que las propiedades químicas de un átomo están sujetas al número de sus electrones planetarios, el torio y el radiotorio tienen el mismo comportamiento químico, sea cual fuere su diferencia en peso atómico (232 y 228 respectivamente).
Los isótopos de un elemento se identifican por su peso atómico, o número másico. Así, el torio corriente se denomina torio 232, y el radiotorio, torio 228. Los isótopos radiactivos del plomo se distinguen también por estas denominaciones: plomo 210 (radio D), plomo 214 (radio B), plomo 212 (torio B) y plomo 211 (actinio B).

Se descubrió que la noción de isótopo podía aplicarse indistintamente tanto a los elementos estables como a los radiactivos. Por ejemplo, se comprobó que las tres series radiactivas anteriormente mencionadas terminaban en tres formas distintas de plomo. La serie del uranio acababa en plomo 206, la del torio en plomo 208 y la del actinio en plomo 207. cada uno de estos era un isótopo estable y corriente del plomo, pero los tres plomos diferían por su peso atómico.
Mediante un dispositivo inventado por cierto ayudante de J. J. Thomson, llamado Francis William Aston, se demostró la existencia de los isótopos estables. En 1.919, Thomson, empleando la versión primitiva de aquel artilugio, demostró que el neón estaba constituido por dos variedades de átomos: una cuyo número de masa era 20, y otra con 22. El neón 20 era el isótopo común; el neón 22 lo acompañaba en la proporción de un átomo cada diez. Más tarde se descubrió un tercer isótopo, el neón 21, cuyo porcentaje en el neón atmosférico era de un átomo por cada 400.

distintos isótopos
Entonces fue posible, al fin, razonar el peso atómico fraccionario de los elementos. El peso atómico del neón (20, 183) representaba el peso conjunto de los tres isótopos, de pesos diferentes, que integraban el elemento en su estado natural. Cada átomo individual tenía un número másico entero, pero el promedio de sus masas (el peso atómico) era un número fraccionario.
Aston procedió a mostrar que varios elementos estables comunes eran, en realidad, mezclas de isótopos. Descubrió que el cloro, con un peso atómico fraccionario de 35’453, estaba constituido por el cloro 35 y el cloro 37, en la proporción de cuatro a uno. En 1.922 se le otorgó el premio Nobel de Química.
En el discurso pronunciado al recibir el premio, Aston predijo la posibilidad de aprovechar la energía almacenada en el núcleo atómico, vislumbrando ya las futuras y nefastas bombas y centrales nucleares. Allá por 1.935, el físico canadiense Arthur Jeffrey Dempster empleó el instrumento de Aston para avanzar sensiblemente en esa dirección; demostró que 993 de cada 1.000 átomos de uranio eran de uranio 238 (no válido para combustible nuclear). Y muy pronto se haría evidente el profundo significado de tal descubrimiento.

Sí, sólo el 7 por 1000 del uranio existente en la Tierra, es combustible nuclear, es decir, Uranio 235. El resto, es Uranio 238 que hay que reciclarlo en un Acelerador Generador para convertirlo en Plutonio 239 que nos sirva como combustible nuclaer de fisión.
Así, después de estar siguiendo huellas falsas durantes un siglo, se reivindicó definitivamente la teoría de Prout. Los elementos estaban constituidos por bloques estructurales uniformes; si no átomos de hidrógeno, sí, por lo menos, unidades con masa de hidrógeno.
¿Qué no será capaz de inventar el hombre para descubrir los misterios de la naturaleza?
emilio silvera
Jul
28
Las Sinfonías de los Agujeros Negros binarios
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (24)
Comments (24)
Lo que nos cuentan Kip S. Thorne y otros especialistas en Agujeros negros nos posibilitan para entender algo mejor los mecanismos de estos extraños objetos que aún esconden misterios que no hemos sabido resolver. Está claro que muchas de las cosas que sobre agujeros negros podemos leer, son en realidad, especulaciones de cosas que se deducen por señales obervadas pero que, de ninguna manera, se pueden tomar como irrefutables verdades, más bien, las tomaremos como probables o muy probables de acuerdo a los resultados obtenidos de muchos experimentos y, ¿por qué no? de muchas horas de prácticas teóricas y pizarras llenas de ecuaciones que tratan de llegar al fondo de un saber que, desde luego, nos daría la clave de muchas cuestiones que en nuestro Universo son aún desconocidas.

En el corazón de una galaxia lejana, a más de 1.000 millones de años-luz de la Tierra y hace 1.000 millones de años, se acumuló un denso aglomerado de gas y cientos de millones de estrellas. El aglomerado se contrajo gradualmente, a medida que algunas estrellas escapaban y los 100 millones de estrellas restantes se hundían más hacia el centro. Al cabo de 100 millones de años, el aglomerado se había contraído hasta un tamaño de varios años-luz, y pequeñas estrellas empezaron, ocasionalmente, a colisionar y fusionarse, formando estrellas mayores. Las estrellas mayores consumieron su combustible y luego implosionaron para formar agujeros negros; y, en ocasiones, cuando dos de estos agujeros pasaban uno cerca del otro, quedaban ligados formando pares en los que cada agujero giraba en órbita alrededor del otro.
Cuando se forma un par de agujeros negros binarios semejantes, cada agujero crea un pozo profundo (intensa curvatura espacio-temporal) en la superficie insertada y, a medida que los agujeros giran uno en torno al otro, los pozos en órbita producen ondulaciones de curvatura que se propagan hacia afuera a la velocidad de la luz. Las ondulaciones forman una espiral en el tejido del espacio-tiempo en torno al sistema binario, muy semejante a la estructura espiral del agua que procede de un aspersor de cesped que gira rápidamente. Los fragmentos de curvatura forman un conjunto de crestas y valles en espiral en el tejido espacio-temporal.

Puesto que la curvatura-espaciotemporal es lo mismo que la gravedad, estas ondulaciones de curvatura son realmente ondas de gravedad, u ondas gravitatorias. La Teoría de la Relatividad General de Einstein predice, de forma inequívoca, que tales ondas gravitatorias deben producirse siempre que dos agujeros negros orbiten uno en torno al otro.
Cuando parten hacia el espacio exterior, las ondas gravitacionales producen una reacción sobre los agujeros de la misma forma que una bala hace retroceder el fusil que la dispara. El retroceso producido por las ondas aproxima más los agujeros y les hace moverse a velocidades mayores; es decir, hacen que se muevan en una espiral que se cierra lentamente y hace que se vayan acercando el uno hacia el otro. Al cerrarse la espiral se genera poco a poco energía gravitatoria, una mitad de la cual va a las ondas y la otra mitad va a incrementar las velocidades orbitales de los agujeros.
Jul
27
¿Quién nos observa?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en ¡No estamos sólos! ~
Clasificado en ¡No estamos sólos! ~
 Comments (0)
Comments (0)

En galaxias lejanas de cientos de miles de millones de estrellas y en otras de menor volumen pero no por ello menos interesantes, existen extraños mundos que, aunque diferentes al nuestro, también viven y se nutren de la radiación y la luz estelar que les llega. Unos tienen soles azules y otros blancos, también los hay amarillos como el nuestro y muchos de ellos son rojos. Cada una de esas estrellas, configuran el color de sus respectivos mundos y los hace de color mortecino, de un azulado brillante o incluso, en ocasiones, de un color que influye en la atmósfera del planeta hasta hacerlo parecer de sangre. También los hay, como el nuestro, son luminosos y están alumbrados por estrellas blanco-azuladas que le dan un tono de exquisita presencia.

No todos los planetas que alberguen alguna clase de vida, ni en nuestra Galaxia ni en otras lejanas, tienen que ser como la Tierra. Existen planetas en los que se nos encogería el corazón por su aspectos terrorífico y de inabitable naturaleza, mientras que otros, nos parecerían una fantasía sacada de esos cuentos de hadas que de ñinos podíamos leer, tal es su belleza natural. En la Tierra tenemos muchas imágenes de lugares que hacen honor a ese pensamiento.

De la misma manera que existen estrellas de mil tipos diferentes, así ocurre con los mundos que podemos encontrar repartidos por el universo orbitando estrellas que los configuran de mil diferentes maneras. Si nos fijamos en nuestro planeta que ha hecho posible nuestra presencia aquí, en el que junto a miles de otras especies hemos evolucionado, veremos que se han dado unas condiciones específicas para que todo eso sea posible.
Hemos podido llegar a un estado de evolución “aceptable” y alcanzado un nivel tecnológico que va más allá de lo que, hace sólo 200 años nos pudiéramos haber imaginado. Desde comienzo de la década de 1960, los programas de TV han emitido desde la Tierra hacia el espacio a un nivel de medio millón de watios. En la actualidad, la energía total emitida por las emisoras de televisión de todo el mundo es muy superior a los mil millones de watios. Durante los últimos quince años, esa cobertura expansiva de las emisoras de televisión, emitiendo desde la Tierra a la velocidad de la luz, ha podido llegar hasta centenares de estrellas y de mundos.

Enormes radares situados por todo el mundo lanzando ondas han podido ser la evidencia inequívoca de que aquí, en la Tierra, existen seres inteligentes que tratan de captar señales venidas del espacio exterior, de vigilar los posibles peligros que nos puedan llegar de mñás allá de los confines del Sistema solar, o, de captar esas señales que denoten la presencia de otros seres inteligentes que, situados en otros mundos lejanos, nos quieren decir alguna cosa o transmitir algún mensaje. Nosotros ya lo hemos intentado y continuamos haciendolo.
¿Cómo serán ellos?
Lo cierto es que hemos llegado a comprender que la vida en la Tierra, toda sin excepción está basada en el Carbono y, como también sabemos que las leyes del Universo son las mismas en todas partes, es lógico pensar que lo que pasó aquí habrá podido pasar allí, en cualquier planeta lejano situado en nuestra Galaxia o en cualquiera de la multitud de galaxias que conforman nuestro universo en el que cientos de miles de millones de mundos, no pueden estar vacíos y carentes de vida.

Todas esas señales y las que emitimos con nuestro quehacer diario, hacen que nuestro planeta brille hasta parecer un ascua encendida en la oscuridad . Las frecuencias de televisión y las bandas de FM de las emisoras de radio nos delatan ante posibles inteligencias en otros mundos. Radioastrónomos situados en otros sistemas solares notarán, al enfocar sus antenas en nuestra dirección, una emisión de energía y advertirán que, en esta estrella amararilla, existe una sociedad científicamente avanzada.

El gráfico de AbstruseGoose (después del salto) nos muestra lo que las civilizaciones extraterrestres estarían viendo en este momento si pudieran monitorear trasmisiones de televisión de la Tierra, de esas trasmisiones del pasado que ingresaron al espacio y se propagan a la velocidad constante de c (la velocidad de la luz en el vacío).
Claro que nuestras señales televisivas le dicen a los extraterrestres mucho más que todo eso. A partir de sutiles cambios en las frecuencia de las señales provocados por la rotación de la Tierra, podrían deducir la distancia que hay entre la Tierra y el Sol, la probable temperaturta de la superficie de nuestro planeta y, a partir de aquí, que clase de vida puede haber en la Tierra. ¡Sabrían de nosotros mucho más que nosotros sabemos de ellos! Bueno, en realidad, de ellos no sabemos nada.

Si los astrónomos extraterrestres de otros sistemas solares han estado haciendo un seguimiento de nuestros progresos, tienen ya prueba de que esta vida ha atravesado ya un importante umbral tecnológico, el umbral de las comunicaciones de radio. Los científicos extraterrestres pueden deducir a partir de su propia experiencia que esa conquista puede verse pronto continuada por un dominio de los viajes por el espacio que es la siguiente escala perseguida. Primero de un planeta a otro cercano. En nuestro caso, digamos a Marte, y, a continuación, y no mucho después. Comenzarán los viajes que nos llevarán a los confines del Sistema Solar en busca de otras fronteras. Sin que nos demos cuenta, ya hemos enviado el mensaje de nuestra presencia que es el precursor de nuestra entrada en la Comunidad Galáctica.

Si realmente existen esos seres que imaginamos en otros mundos y, si como es lógico pensar, al igual que nosotros han podido evolucionar hasta alcanzar aceptables niveles del saber sobre la Naturaleza y los secretos del Universo, también habrán podido alcanzar una avanzada tecnología que, más o menos como la nuestra, les posibilite para enviar señales y hacer viajes espaciales que (no me extrañaría nada) estuvieran ya camino hacia nosotros.

Millones de mundos que, como el nuestro, brillaran en la noche delatando la presencia de Sociedades avanzadas que, situadas en grandes ciudades dejan transcurrir sus vidas mientras, también como nosotros, no dejan de investigar y de hacerse preguntas que, tampoco ellos, saben contestar. El saber del mundo, de los mundos, está repartido por todo el Universo que es, en definitiva, el que tiene todas esas respuestas que buscamos.

Muchas veces me hago esta pregunta: ¿De qué estrella vendrá esa primera señal de inteligencia que esperamos? Las civilizaciones que la envíe ¿a qué distancia estará, cómo será su mundo, cuánto tiempo ha tardado en llegar a nosotros, y, cuando la podamos descifrar, y contestemos, cuánto tardarán en tener la respuesta? Incluso es posible -seguramente lo normal-, que esas señales hayan sido enviadas ya por ambas partes y que, ni ellos ni nosotros, debido a las distancias que nos separan, la hemos podido recibir. ¡Qué frustración, pensar que eso es así y no poder hacer nada por remediarlo!
Ya hablamos el otro día de las estrellas cercanas, las que estaban situadas dentro de un radio de unos doce años-luz y de las posibilidades que podían existir de que, en alguna de ellas (de sus planetas), pudiera existir alguna clase de vida. La presencia de vida inteligente en el inmenso universo, debe ser una cosa cotidiana, nada excepcional. Sin embargo, tal como están dispuestas las cosas, lo que no parece tan cotidiano es, el hecho de que, entre civilizaciones inteligentes nos podamos encontrar, las inconmensurables distancias que nos pueden separar son… ¡casi inaccesibles! y, el tiempo necesario para recorrerlas, vería pasar ante él a muchas generaciones de individuos antes de que, entre ellos, pudiera darse ese contacto tantas veces imaginado.


Es poco probable que los que, ilusionados, lanzaron la señal hacia otros mundos. El mensaje que les hermanaría gracias a la inteligencia, pudiera ver realizados sus sueños de recibir una respuesta. El Proyecto OZMA y SETI son un buen ejemplo de ello. Y, por otra parte, no todas las estrellas están en disposición de poder dar a sus planetas lo que estos necesitan para albergar la vida. Pensemos que una estrella si es muy joven, digamos de unos cientos de millones de años, radiará en el ultravioleta con tal virulencia que, encontrar vida en sus inmediaciones sería imposible. Si por el contraria es una estrella vieja que, al final de su vida está a punto de explotar como supernova… tampoco parece que su entorno sea el adecuado.
Las estrellas y los mundos que puedan ser idóneas para que la vida esté presente, tendrán que tener esas condiciones mínimos exigidas para que, el agua esté presente, para que una atmósfera aceptablemente importante configure el planeta, que éste tenga una serie de parámetros de magnetismo, tectónica, oceános y otros que lo haga un planeta vivo, que la luz de la estrella lo caliente sin achicharrarlo… Si todo eso y algunas cosas más están presentes… La vida también lo estará.
Pero lo cierto es que, aunque la lógica nos dice que están ahí… ¡Seguimos sin recibir señales de que la vida está ahí fuera! El principal problema de que así sea, está en las distancias que nos separan y, simplemente tenemos que pensar que cualquier estrella orbitada por planetas está a muchos años-luz de nosotros y, las que puedan tener alguna posible forma de vida inteligente, no sabemos uán lejos podrán estar situadas y, para llegar a nosotros, esas señales, necesitan recorrer el espacio que nos separa a la máxima velocidad que el universo permite, es decir, la velocidad de la luz de 299.792,458 km/s. Un viaje algo lento para que llegue a nosotros en un tiempo prudencial.
Seguramente, para cuando ese contacto se pueda producir, las civilizaciones que se encuentren, tendrán otros medios más avanzados que el de los viajes clásicos de las naves viajeras tal como las conocemos y, serán otras naves y otros caminos los que serán recorridos para viajar entre las estrellas. El Hiperespacio y los agujeros de gusano son dos buenas opciones pero… ¡habrá tántas!
emilio silvera
















 Totales: 74.379.513
Totales: 74.379.513 Conectados: 21
Conectados: 21

























