¡La Física! Que nos dice como es la Naturaleza

Hay una anécdota que se cuenta y que ilustra la dificultad de muchos para reconciliar el trabajo de Eddington sobre las constantes fundamentales con sus monumentales contribuciones a la relatividad general y a la astrofísica. La historia la contaba Sam Goudsmit referente a él mismo y al físico holandés Kramers:

                                                                             Samuel Abraham Goudsmit, George Uhlenbeck y Hendrik Kramers

“El gran Arthur Eddington dio una conferencia sobre su derivación de la constante de estructura fina a partir de una teoría fundamental. Goudsmit y Kramers estaban entre la audiencia.  Goudsmit entendió poco pero reconoció que era un absurdo inverosímil. Kramers entendió mucho y reconoció que era un completo absurdo. Tras la discusión, Goudsmit se acercó a su viejo amigo y mentor Kramers y le preguntó: ¿Todos los físicos se vuelven locos cuando se hacen mayores? Tengo miedo. Kramers respondió, “No Sam, no tienes que asustarte. Un genio como Eddington quizá puede volverse loco pero un tipo como tú sólo se hace cada vez más tonto”.

“La historia es la ciencia de las cosas que no se repiten”.

Paul Valéry

Arthur Stanley Eddington (1882-1944)

El mayor misterio que rodea a los valores de las constantes de la naturaleza es sin duda la ubicuidad de algunos números enormes que aparecen en una variedad de consideraciones aparentemente inconexas. El número de Eddington es un ejemplo notable. El número total de protones que hay     dentro del alcance del universo observable esta próximo al número

10⁸⁰

Si preguntamos ahora por la razón entre las intensidades de las fuerzas electromagnéticas y gravitatoria entre dos protones, la respuesta no depende de su separación, sino que es aproximadamente igual a

10⁴⁰

En un misterio. Es bastante habitual que los números puros que incluyen las constantes de la naturaleza difieran de 1 en un factor del orden de 10², ¡pero 10⁴⁰, y su cuadrado 10⁸⁰, es rarísimo! Y esto no es todo. Si seguimos a Max Planck y calculamos en valor estimado para la “acción” del universo observable en unidades fundamentales de Planck para la acción, obtenemos.

10¹²⁰

Algunos llegan a afirmar que, el Universo es plano e indican que la energía oscura es probablemente la constante cosmológica de Einstein…¡Vivir para ver!

Ya hemos visto que Eddington se inclinaba a relacionar el número de partículas del universo observable con alguna cantidad que incluyera la constante cosmológica. Esta cantidad ha tenido una historia muy tranquila desde esa época, reemergiendo ocasionalmente cuando los cosmólogos teóricos necesitan encontrar una manera de acomodar nuevas observaciones incómodas.  Recientemente se ha repetido este escenario. Nuevas observaciones de alcance y precisión sin precedentes, posibilitadas por el telescopio espacial Hubble trabajando en cooperación con telescopios sensibles en tierra, han detectado supernovas en galaxias muy lejanas. Su pauta de brillo y atenuación característica permite deducir su distancia a partir de su brillo aparente. Y, sorprendentemente, resulta que están alejándose de nosotros mucho más rápido de lo que cualquiera esperaba. La expansión del universo ha pasado de ser un estado de deceleración a uno de aceleración. Estas observaciones implican la existencia de una constante cosmológica positiva (Λ⁺). Si expresamos su valor numérico como número puro adimensional medido en unidades del cuadrado de la longitud de Planck, entonces obtenemos un número muy próximo a

10^-120

                                                            Nunca se ha encontrado un número más pequeño en una investigación física real.

Hablar del Universo en todo su conjunto…No es nada fácil. Podemos hablar de parcelas, de elementos por separado y, una vez individualizados, juntarlos para tener una perspectiva de su conjunto que…No siempre podemos comprender. ¡Es tanto lo que nos quiere decir! que, comprenderlo, nos llevará algún tiempo.

¿Qué vamos a hacer con todos estos grandes números? ¿Hay algo cósmicamente significativo en 10⁴⁰ y sus cuadrados y cubos?

Hermann Weyl

La aparición de algunos de estos grandes números ha sido una fuente de sorpresas desde que fue advertida por vez primera por Hermann Weyl en 1.919. Eddington había tratado de construir una teoría que hiciera comprensible su aparición, pero no logró convencer a un número significativo de cosmólogos de que estaba en la vía correcta. Pero sí convenció a la gente de que había algo que necesitaba explicación. De forma inesperada, fue precisamente uno de sus famosos vecinos de Cambridge quien escribió a la revista Nature la carta que consiguió avivar el interés por el problema con una idea que sigue siendo una posibilidad viable incluso hoy.

Paul Dirac

Paul Dirac ocupó la cátedra lucaciana de matemáticas en Cambridge durante parte del tiempo en que Eddington estuvo viviendo en los observatorios. Las historias que se cuentan de Paul Dirac dejan muy claro que era un tipo con un carácter peculiar, y ejercía de matemático las 24 h. del día. Se pudo saber que su inesperada incursión en los grandes números fue escrita durante su viaje de novios (Luna de miel), en febrero de 1937.

Aunque no muy convencido de las explicaciones de Eddington, escribió que era muy poco probable que números adimensionales muy grandes, que toman valores como 10⁴⁰ y 10⁸⁰, sean accidentes independientes y no relacionados: debe existir alguna fórmula matemática no descubierta que liga las cantidades implicadas. Deben ser consecuencias más que coincidencias.

Esta es la hipótesis de los grandes números según Dirac:

“Dos cualesquiera de los números adimensionales muy grandes que ocurren en la naturaleza están conectados por una sencilla relación matemática, en la que los coeficientes son del orden de la unidad”.

Los grandes números de que se valía Dirac para formular esta atrevida hipótesis salían del trabajo de Eddington y eran tres:

N₁ = (tamaño del universo observable) / (radio del electrón)

= ct (e²/m_ec²) ≈ 10⁴⁰

N₂ = Razón fuerza electromagnética-a-gravitatoria entre protón y electrón

= e²/Gm_e m_p ≈ 10⁴⁰

N = número de protones en el universo observable

= c³t/Gm_p ≈ 10⁸⁰

Aquí t es la edad actual del universo, m_e es la masa de un electrón, m_p es la masa de un protón, G la constante de gravitación, c la velocidad de la luz y e la carga del electrón.

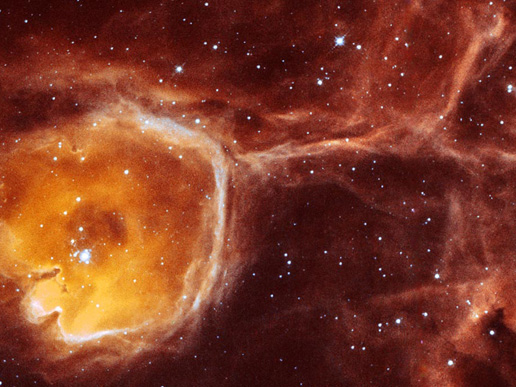
El Universo no puede ser estático

Según la hipótesis de Dirac, los números N₁, N₂y raizN eran realmente iguales salvo pequeños factores numéricos del orden de la unidad. Con esto quería decir que debe haber leyes de la naturaleza que exijan fórmulas como N₁ = N₂, o incluso N₁ = 2N_2. Un número como 2 ó 3, no terriblemente diferente de 1 está permitido porque es mucho más pequeño que los grandes números implicados en la fórmula; esto es lo que él quería decir por “coeficientes….  del orden de la unidad”.

Esta hipótesis de igualdad entre grandes números no era en sí misma original de Dirac. Eddington y otros habían escrito antes relaciones muy semejantes, pero Eddington no había distinguido entre el número de partículas del universo observable, que se define como una esfera centrada en nosotros con un radio igual a la velocidad de la luz multiplicada por la edad actual del universo, o lo que es lo mismo:

Trayectoria del Universo observable.

La trayectoria del llamado Universo Observable (y del cual somos su centro al recorrer su geodésica en la geometría espacio-temporal) tiene la forma perimetral de una gota (forma de media lemniscata; cosa curiosa, lemniscata: figura curva ∞ usada como el símbolo de infinito ¿?) que al girarla 45 ° y desarrollar un cuerpo de revolución, se obtienen dos campos toroidales cual si fuesen imágenes antagónicas (una reflejada) de una fuente (surtidor – sumidero cada uno), correspondiendo uno al campo material y el otro al antimaterial.

Lo están ocupando en su totalidad, se retroalimentan a sí mismos en la Hipersingularidad (punto de contacto de los dos campos, principio y fin de ambos flujos donde reacciona la materia y la antimateria con la finalidad de mantener separados ambos universos con el adicional resultado de impulsar nuevamente a los fluidos universales de ambos campos a recorrer la finita trayectoria cerrada (geodésica) siendo el motor propulsor universal de dos volúmenes dinámicos, finitos pero continuos).

Universo observable: R = 300.000 × 13.500.000.000

El cambio radical expuesto por Dirac en su hipótesis de grandes números es que nos exige que creamos que un conjunto de constantes tradicionales de la naturaleza, como N₂, debe estar cambiando a medida que el universo envejece en el tiempo, t:

N₁ ≈ N₂ ≈ raizN α t

Puesto que Dirac había incluido dos combinaciones que contenían la edad del universo, t, en su catálogo de grandes números, la relación que él propone requiere que una combinación de tres de las constantes de la naturaleza tradicionales no sea constante en absoluto, sino que su valor debe aumentar continuamente a medida que el universo se hace más viejo, de modo que

e²/Gm_p α t

Dirac decidió acomodar este requisito abandonando la constancia de la constante de gravitación de Newton, G. Sugirió que estaba decreciendo en proporción directa a la edad del universo en escalas de tiempo cósmicas, como

G α 1/t

Así pues, en el pasado G era mayor y en el futuro será menor que lo que mide hoy. Ahora veremos que N₁ ≈ N₂ ≈ raizN α t y la enorme magnitud de los tres grandes números es una consecuencia de la gran edad del universo: todas aumentan con el paso del tiempo.

                                                           Que a estas alturas no sepamos a ciencia cierta en qué clase de universo estamos…

La propuesta de Dirac provocó un revuelo entre un grupo de científicos vociferantes que inundaron las páginas de las revistas especializadas de cartas y artículos a favor y en contra. Dirac, mientras tanto, mantenía su calma y sus tranquilas costumbres, pero escribió sobre su creencia en los grandes números cuya importancia encerraba la comprensión del universo con palabras que podrían haber sido de Eddington, pues reflejan muy estrechamente la filosofía de la fracasada “teoría fundamental”.

“¿No cabría la posibilidad de que todos los grandes sucesos presentes correspondan a propiedades de este Gran Número [10⁴⁰] y, generalizando aún más, que la historia entera del universo corresponda a propiedades de la serie entera de los números naturales…? Hay así una posibilidad de que el viejo sueño de los filósofos de conectar la naturaleza con las propiedades de los números enteros se realice algún día”.

Edward Teller

La propuesta de Dirac levantó controversias entre los físicos, y Edward Teller en 1.948, demostró que si en el pasado la gravedad hubiera sido como dice Dirac, la emisión de la energía del Sol habría cambiado y la Tierra habría estado mucho más caliente en el pasado de lo que se suponía normalmente, los océanos habrían estado hirviendo en la era precámbrica, hace doscientos o trescientos millones de años, y la vida tal como la conocemos no habría sobrevivido, pese a que la evidencia geológica entonces disponible demostraba que la vida había existido hace al menos quinientos millones de años. Sin embargo, más tarde con más datos y estudios realizados, se comprobó que la vida, era casi tan antigüa como la misma Tierra, lleva aquí con nosotros 4.000 millones de años.

Claro que, eso es así (que lo es) porque las Constantes Cosmológicas son eso, “Constantes” y, no han variado a lo largo de los miles de millones de años que el Universo existe. Si alguna de ellas, pongamos por caso el electrón, variará su carga en sólo una diezmillonésima, la vida no podría exisitr. Los átomos, como sabeis, están compuestos por el núcleo masivo formado por necleones -protones y neutrones- y, los protones tienen una carga eléctrica positiva. Ese núcleo es rodeado por el mismo número de electrones que tiene el núcleo de protones y, como la carga eleéctrica del electrón es negativa y similar en valor a la del protón, el átomo queda equilibrado y estable haciendo posible que se junen para formar células, moléculas, sustancias y cuerpos…es decir, desde un grano de arena hasta una montaña, una estrella, una galaxia o los seres vivos como nsootros que, de ser las constantes fundamentales del Universo distintas, no estaríamos aquí.

emilio silvera

[?]