Sep
5
¿Cuántas Dimensiones existen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Un Universo con dimensiones extra ~
Clasificado en Un Universo con dimensiones extra ~
 Comments (30)
Comments (30)
La pregunta de arriba tiene una clara respuesta para casi todo el mundo: “Tres: alto, ancho y profundo”. Desde finales del siglo XIX y principios del XX sabemos que a esas tres tenemos que añadir una cuarta, el tiempo, íntimamente ligada a las tres espaciales mediante las leyes de la relatividad especial, en ausencia de campos gravitatorios, o la relatividad general en presencia de estos.
Leyendo como es habitual la Revista Española de Física que me envían como Socio Numerario, uno de los artículos me llamó la atención, lo escribe D. José Santiago (CAFPE y Departamento de Física Teórica y del Cosmos) de la Universidad de Granada, en este trabajo trata de mostrar al lector que el número de dimensiones espacio-temporales podría ser mayor que esas cuatro.
La existencia de dichas dimensiones extra pueden ayudarnos a comprender algunas de las misteriosas propiedades de la física de las partículas elementales, en cuyo caso, su descubrimiento experimental estaría a la vuelta de la esquina.
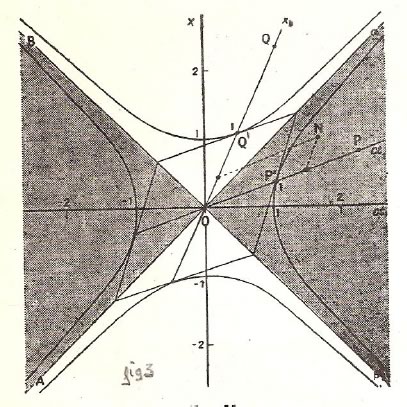
Representación de Minkowski en el que obviamos explicar el galimatias de letras, números y coordenadas que están ahí implicados.
La idea de nuevas dimensiones espaciales no es nueva. De hecho, pocos años después de que Einstein presentase la teoría de la relatividad general, Kaluza primero, y Klein después que la perfeccionó, propusieron una teoría cinco-dimensional (con una dimensión espacial extra) para unificar las interacciones gravitatorias y electromagnética. La idea consistía en que el fotón, la partícula que media las interacciones electromagnéticas, podría ser una componente a lo largo de la quinta dimensión del gravitón, mediador de interacciones gravitatorias. Así, la invariancia gauge asociada a la electrodinámica no es más que un remanente de la invariancia bajo reparametrizaciones propia de la relatividad general.
Nosotros, los Humanos, estamos conformados con una mente tridimensional y, hacernos una idea de ese universo de más dimensiones se nos hace muy cuesta arriba, hasta tal punto es así que, ni en nuestra imaginación podemos modelar la imagen que nos lleve hasta ese universo decadimensional del que hablan las nuevas teorías. No podemos oir ese mundo, menos lo podemos describir y, verlo es sólo un suelo de la imaginación.

La teoría de Kaluza-Klein no consigue reproducir con éxito los datos experimentales y fue esencialmente abandonada hasta finales de los setenta y principio de los ochenta, en la que estudios de supersimetría y supergravedad y sobre todo la formulación de teoría de cuerdas, que requiere al menos nueve dimensiones espaciales para para ser consistente, supusieron un revulsivo en el que modelos con dimensiones extra volvieron a considerarse una seria posibilidad.
Esas dimensiones extra de las que hablan tendrían que encontrarse en el orden de la eslacala de Planck, es decir, Lp ≈ 1,6 x 10 -35 m., lo que garantiza que no estuviesen excluidas experimentalmente, pero al mismo tiempo las hacía totalmente irrelevantes desde el punto de vista denomenológico.
A finales de los noventa se produjo una revolución liderada por los artículos seminales de Arkani-Hamed, Dimopoulos y Dvali por un lado y Randall y Sandrum por otro. A consecuencia de estos trabajos, la comunidad se dio cuenta de que dimensiones extra de tamaño macroscópico, e incluso infinitas, no están necesariamente excluidas experimentalmente. También se vio que dimensiones extra más pequeñas, del tamaño de la escala electrodébil e incluso de la escala de Planck podían tener consecuencias espectaculares en los experimentos de partículas en funcionamiento actualmente (o planeados para un futuro cercano) y al mismo tiempo explicar, de manera satisfactoria, muchos de los minterios actuales de la física de partícula.

Nuestro Universo, además de las tres dimensiones conocidas, tendría seis dimensiones más ocultas, según un modelo matemático que ha recreado las condiciones iniciales de la formación del Universo.
¿En qué nos pueden ayudar las dimensiones extra?
Uno de los mayores misterios de la física de partículas es el mecanismo por el que la simetría electrodébil se rompe espontáneamente. En dicha rotura -que distinque entre la simetría débil, espontáneamente rota y por tanto con interacciones de corto alcance, y la simetría electromagnética, que no se rompe y por tanto involucra intercciones de alcance infinito- radica origen de la masa de las partículas elementales. Ignoramos por qué esta rotura ocurre a una escala de energía mucho menor (unos quince órdenes de magnitud) que la masa de Planck, que sería su valor natural. A esta enorme diferencia de escalas se le conoce como el problema de la jerarquía y es uno de los argumentos más sólidos para esperar la aparición de nueva física en los experimentos actuales de partículas como el Tevatron en Fermilab o el LHC en el CERN. Otro aspecto que no sabemos explicar de manera satisfactoria es el patrón observado de masas y ángulos de mezcla de los fermiones (las partículas de materia). Se han observado seis “sabores” de quarks con masas que van desde los ~4 x 10-3 GeV de los quarks up y down (un GeV o gigaelectronvoltio es aproximadamente la masa del protón) hasta los 170 GeV del quark top. Si incluimos el sector de leptones, la diferencia de masas es incluso mayor puesto que el más ligero de los leptones cargados, el electrón, posee una masa de 0.5 x 10-3 GeV y los neutrinos son aún más ligeros, con una masa menor que 10-10 GeV. Las mezclas entre distintos sabores son pequeñas y jerárquicas en el sector de quarks y grandes en el sector leptónico. La replicación de familias (quarks y leptones se distribuyen en tres copias o familias, idénticas excepto por el valor de sus masas), la asimetría bariónica del universo o la existencia de materia oscura son ejemplos de otras propiedades que no tienen explicación ene le contexto del odelo estándar de partículas. La existencia de dimensiones extra podrían explicar muchas de estas propiedades de manera natural, siendo compatible con las cotas experimentales y prediciendo una rica fenomenología en colisionadores de partículas.

Observación de dimensiones extra
La manera más sencilla de responder la pregunta “Si existen las dimensiones extra, ¿por qué no las hemos visto todavía?” es que éstas son demasiado pequeñas. Una simple analogía sería cómo la cuerda de un equilibrista puede parecer uni-dimensional para un observador que mira desde lejos mientras que una homriga que camina sobre la misma cuerda la aprecia como una superficie bi-dimensional. ¿Cómo podemos “acercarnos” en experimentos e física de partículas para ver las dimensiones extra? Los experimentos de física de partículas son fundamentalmente experimentos de colisión, en los que aceleramos haces de partículas hasta que tienen una energía determinada y los hacemos colisionar, estudiando el resultado de dicha colisión. La manera de hacer más potente nuestro “microscopio” es pues aumentar la energía de dichas colisiones. Efectivamente energía (o más propiamente momento) y distancia son variables conjugadas de manera que cuanto mayor es el momento de una partícula, menor es su longitud de onda asociada y por tanto más sensible es a los detalles a cortas distancias del espacio-tiempo. Los principales aceleradores de partículas funcionando actualmente alcanzan una energía máxima de 1960 GeV (Tevatrón) y 7000 GeV (LHC) aunque la mayor parte de las colisiones ocurren a energías algo menores.

Para ver cómo experimentos a suficiente energía nos permitirían observar las dimensiones extra, imaginemos un modelo con una dimensión extra circular de radio R. Una partícula de masa cero en dicho espacio viene representada por un campo cinco-dimensional (por simplicidad consideramos una partícula escalar),
Φ (t, x, y, z, ω),
donde hemos denotado con un ω la dimensión extra y la condición de capa de masas es
p2t – p2x – p2y – p2z – p2ω = 0.
El hecho de que la dimensión extra sea periódica implica que el momento a lo largo de dicha dirección está cuantizado (recordemos que el momento es el generador de las traslaciones y traslaciones relacionadas por un múltiplo entero de 2πR tienen que dar la misma configuración)
Pω= n/R, n=0,1,2… .
La ecuación (2) puede ser interpretada como la condición de capa de masas de una partícula cuatri-dimensional, con una masa igual al momento (cuatizado) en la dimensión extra
mn = √p2t – p2x – p2y – p2z = n/R.
De hecho, el campo de cinco-dimensional se puede expandir en serie de Fourier. Es decir, lo que no podemos explicar con palabras lo podemos hacer con números, un lenguaje que, desgraciadamente, no todos dominamos.

Es entonces fácil ver que cada uno de los coeficientes de la serie de Fourier es un campo cuatri-dimensional, que podemos interpretar como una partícula con masa dada por (4). El resultado es que un campo extra-dimensional se puede ver como una torre infinita de campos cuatri-dimensionales, los modos de KK, con masas crecientes, proporcionales al inverso del tamaño de las dimensiones extra. Las partículas conocidas corresponderían a los modos con n=0 (sin masa antes de la rotura espontánea de la simetría electrodébil) y el efecto de las dimensiones extra son los modos de KK que sólo se pueden producir si nuestro experimento tiene una energía del orden de su masa. Es decir, que dimensiones extra suficientemente pequeñas tienen modos de KK demasiado pesados para producirse experimentalmente y por tanto las dimensione extra no son observables. Aunque esta imagen es bastante genérica, los detalles pueden variar de unos modelos a otros. Por ejemplo, si el espacio-tiempo extra-dimensional tiene curvatura, las masas de los modos KK no tienen por qué ser proporcionales al inverso del tamaño de las dimensiones extra (sino tal vez a dicho tamaño convenientemente corrido al rojo debido a los efectos gravitatorios).

Dimensiones extra alabeadas.
El modelo de Randall-Sundrum (RS) [9,10], prototipo de modelos con dimensiones extra alabeadas, consiste en una sección de espacio de Anti-de-Sitter cinco-dimensional. La dimensión extra acaba en dos subespacios cuatridimensionales, denominados branas ultravioleta e infrarroja, respectivamente. La principal asunción que justifica la naturalidad del modelo, es que existe una única escala fundamental, del orden de la escala de Planck. Todos los parámetros dimensionales fundamentales, incluyendo la curvatura del espacio-tiempo o el tamaño de la dimensión extra, son del mismo orden. La escala electrodébil, sin embargo, está naturalmente suprimida con respecto a la escala fundamental debido al enorme corrimiento al rojo que induce la curvatura, resolviendo así el problema de la jerarquía. Este modelo es un ejemplo en el que la curvatura hace que los modos de KK no tengan masas proporcionales al inverso del tamaño de la dimensión extra, sino a su valor corrido al rojo por el efecto de la gravedad que es del orden de la escala electrodébil. Esto quiere decir que, pese a su ínfimo tamaño, las dimensiones extra alabeadas pueden ser descubiertas en el LHC.

No podemos negar que estamos haciendo todo lo posible, sin parar en nada, para encontrar los secretos de la Naturaleza de la Materia y del Universo que nos acoge. ¡Son tántas las cosas que no sabemos! El ser humano, al que le tocó ser poseedor de cierta racionalidad, no debe dejar pasar la oportunidad de, al menos, intentar saber el por qué estamos aquí, como es, ese aquí y, si realmente hay algún destino
Una propiedad general de modelos con dimensiones extra que los hace especialmente atractivos es la localidad en la dimensión extra. Campos cuatridimensionales (los modos de KK) pueden estar localizados en puntos diferentes de la dimensión extra, lo que automáticamente suprime, en ocasiones exponencialmente, los acoplamientos entre ellos. Esto nos permite por ejemplo explicar de forma sencilla la gran diferencia de masas entre unos fermiones y otros o sus patrones de mezcla. La localidd en la dimensión extra, combinada con la fuerte curvatura en el modelo de RS produce un patrón de nueva física extremadamente interesante. En estos modelos, los primeros modos de KK -los más accesibles experimentalmente- están localizados cerca de la brana infrarroja, en la que también se produce la rotura de simetría electro débil y por tanto la masa de los fermiones. Los fermiones ligeros, cuyas propiedades han sido estudiadas experimentalmente con gran detalle sin observar ninguna anomalía, son ligeros porque están localizados lejos de la brana infrarroja y acomplan por tanto débilmente a los primeros modos de KK. Esto explica que sus propiedades no se vean modificadas apreciablemente por las dimensiones extra. El quark top, por contra, es mucho más pesado porque está localizado cerca de la brana infrarroja y por tanto su acomplamiento a los modos de KK es mucho myor. Como resultado, una predicción de estos modelos es que las propiedades del quark top -que aún no han sido medidas con precisión pero que serán objeto de profundo estudio en el LHC- serán modificadas por las dimensiones extra y que los modos de KK asociados a dichas dimensiones se mostrarán fundamentalmente en forma de producción anómala de quarks top.
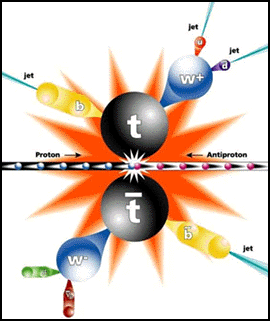
Todas estas propiedades hacen los modelos con dimensiones extra alabeadas muy atractivos, pero cobran una relevancia aún mayor cuando nos damos cuenta de que la famosa conjetura de Maldacena, aplicada a modelos con dimensiones extra alabeadas implica que estos modelos son duales a teorías cuatri-dimensionales fuertemente acopladas. Esto quiere decir que, incluso si las dimensiones extra no existiesen realmente, modelos tipo RS o sus generalizaciones aún pueden serútiles. En efecto, debido a la dualidad nos permiten hacer cálculos cuantitativos que aplican a toerías cuatri-dimensionales en las que, debido al acoplamiento fuerte, no resulta sencillo calcular de otra forma. Usando esta dualidad se han hecho estudios relevantes tanto para cromodinámica cuántica como para teorías de rotura de la simetría electrodébil mediante acoplamiento fuerte, como para modelos de tecnicolor o de Higgs compuesto, por ejemplo.
Es fácil intuir que, si estos modelos están relacionados con modelos fuertemente acoplados, sus restricciones experimentales serán bastante estrictas. Efectivamente, un estudio cuidadoso muestra que, aun usando ciertas simetrías que protegen los observables más sensibles, los modos de KK de los bosones de gauge (las partículas que median las interacciones) tienen que tener una masa del orden de 3500 GeV o mayor, haciéndolos más dificilmente observables en el LHC de lo que originalmente se pensó. Los modos de KK de los fermiones, por otro lado, pueden ser mucho más ligeros y fácilmente observables en el LHC.
Otros modelos de dimensiones.
1.-Dimensiones extra planas a la escala electrodébil.
Otra posibilidad, cuyo interés es fundamentalmente fenomenológico, es que existan dimensiones extra planas de un tamaño un poco inferior a la escala electrodébil. Aunque dichos modelos no resuelvan de por sí el problema de la jerarquía, predicen una fenomenología excitante en el LHC, en ocasiones con señales que pueden simular modelos supersimétricos. La localidad en las dimensiones extra también pueden ser utilizada en dimensiones planas para suavizar comportamientos en rotura espontánea de simetrías gauge o de supersimetría.

2.-Dimensiones accesibles sólo a gravedad.
La interacción gravitatoria, debido a que su intensidad es mucho menor que las otras tres interacciones fundamentales (la fuerte, la débil y la electromagnética) sólo ha podido ser estudiada a distancias del orden de 0.1 mm o mayores. A raíz de esta cota tan poco restrictiva Arkani-Hamed, Dimopoulos y Dvali (ADD) hicieron en 1998 la atrevida propuesta de que podrían existir dimensiones extra hasta de 0.1 mm de tamaño. Para que esta propuesta fuese permitida experimentalmente, las interacciones fundamentales aparte de la gravitatoria, los fermiones y el sector de rotura espontánea de la simetría tenían que estar confinados a un sub-espacio cuatri-dimensional, una brna, de manera que sólo la interacción gravitatoria pudiese propagarse por las dimensiones extra. Con dos dimensiones extra del tamaño máximo permitido se conseguía explicar la debilidad de la interacción gravitatoria comparada con el resto de interacciones (que está relacionado con el problema de la jerarquía) debido a un efecto de dilución de la interacción gravitatoria en el gran volumen (desde el punto de vista microscópico) de las dimensiones extra. Estos modelos abren la puerta a una plétora de descubrimientos, desde la creación de agujeros negros, desaparición de estados en las dimensiones extra o efectos de gravedad cuántica en colisionadores de partículas hasta nuevos efectos en interacciones gravitatorias o experimentos de neutrinos. Un número mayor de dimensiones extra también es posible, aunque si queremos explicar la intensidad de la interacción gravitatoria, su tamaño ha de ser menor y por tanto sus implicaciones experimentales menos relevantes.

Poco después de la propuesta de ADD, se descubrió que si las dimensiones extra son accesibles sólo a la interacción gravitatoria, estas dimensiones no solo pueden tener un tamaño macroscópico, sino que pueden ser incluso infinitas. Una manera de hacer dimensiones extra infinitas compartibles con las restricciones experimentales es asumir que el espacio-tiempo está fuertemente curvado. De hecho, una simple modificación del modelo original de RS, en el que la brana infrarroja es llevada a infinito, predice la siguiente forma del potencial de Newton:
V(r) ~1/r (1+ l2p/r).
El primer término coincide con el potencial de Newton cuatri-dimensional. La fuerte curvatura apantalla el efecto de la dimensión extra infinita, de manera que su presencia no sólo tiene el efecto mostrado por el segundo término, relevante a distancias menores que la longitud de Planck.
Otra posibilidad de tener dimensiones extra infinitas, incluso en espacio plano, fue propuesta por Dvali, Gabadadze y Porrati (DGP). La idea parte de nuevo de modelos en los que el resto de materia e interacciones está confinado a una brana cuatri-dimensional dentro del espacio cinco-dimensional. Si en dicha brana se induce (por efectos cuánticos, por ejemplo) un término de Einstein-Hilbert localizado, con una constante de Planck (l4) diferente de la cinco-dimensional (l5), se forma una nueva escala efectiva
l0= l25/ 2l25
que de nuevo apantalla la dimensión extra. El comportamiento del potencial de Newton pasa de cuatri-dimensional a distancias más cortas que l0 a cinco dimensional a distancias mayores,
V(r)~{1/r, r«l0, l0/r2, r» l0.
Si asumimos que la escala l0 es del orden del tamaño del Universo observable, podríamos usar la transición al comportamiento cinco-dimensional para explicar la actual expansión acelerada del universo. La propuesta original de DGP parece tener ciertos problemas fenomenológicos que inducen inestabilidades aunque todavía se discute si extensiones sencillas de dicho modelo podrían ser compatibles con las observaciones experimentales.
El trabajo se publicó en el Blog de emilio silvera el 24/10/2011.
















 Totales: 75.399.847
Totales: 75.399.847 Conectados: 4
Conectados: 4























el 3 de agosto del 2016 a las 15:11
Pero quedamos en lo mismo, no hay forma de establecer experimentalmente esas supuestas dimensiones por mucho que las matemáticas sean posibles.
el 4 de agosto del 2016 a las 7:50
Si esas dimensiones extra existen, nosotros, seres tridimensionales, no las podemos ver. Algunos, se buscaron el “truco” de decir que, cuando aquel suceso que llamamos Big Bang aconteció, el universo tenía 10 dimensiones, y, cuatro de ellas se expandieron desde ese momento y, las otras seis, quedaron compactas en la dimensión de Planck. Están ahí pero no las podemos ver, y, ellos, los matemáticos, las utilizan como herramienta para elucubrar sus terias. Claro que, de momento, nuestro Universo sigue siendo de 4 dimensiones, tres espaciales y una temporal.
el 14 de enero del 2017 a las 2:19
decian los antiguos cientificos, que el aire es probocado por los arboles al agitar sus ramas, que las moscas nacian espontaneamente de la carne y los frutos de los arboles incluian pajaros y abejas. que todo estaba formado por tierra aire agua y fuego…
lo que se van a reir las futuras generaciines a nuestra costa!
a las 4 dimensiones conocidas, sumen las dimensiones de masa, opacidad, vida, ficcion y temperatura y appa, ya no estan ocultas! pero que si aun les falta aguna dimension, q ya se la localizo yo!
el 14 de enero del 2017 a las 7:24
Amigo Jorge, es cierto que, si miramos hacia atrás en el Tiempo, podemos ver cómo aquellos grandes pensadores del momento atribuían el origen de las cosas a lo que ahora nos parece irrisorio. Sin embargo, no podemos dejar de admitir que, de alguna manera, señalaban a lo que sería la realidad futura y, aunque de manera algo grosera, ellos, nos señalaron el camino de los elementos y del átomo.
En relación a esas dimensiones ocultas… ¡Qué puedo decir! Lo único que se me ocurre es que no podemos negarlas, ya que, nuestra ignorancia es infinita y nuestros conocimientos son muy limitados, quizás algún día, podamos despejar muchas de las dudas que ahora nos hacen pensar en lo que podría ser.
Siempre ha sido así, las teorías del presente tienen que ser cambiadas en el futuro, los nuevos conocimientos así lo exigen.
Saludos cordiales.
el 19 de enero del 2017 a las 0:40
amigo Emilio Silvera:
la ciencia de hoy empieza a parecerse demasiado a la religion de antaño, donde partiendo de verdades evidentes se desarrollan historias poco menos que extrañas, (por no decir absurdas)
la palabra “dimension” hace referencia a algo mesurable, medible, acotable. biene siendo algo asi como una cita. 01/01/2019, 8:49:36, sr. pepito, calle pedrito, numero x, planta y, puerta #, distrito, ciudad, provincia, pais.
eso son 11 dimensiones. que se podrian resumir en 3 de espacio y una de tiempo. y tendriamos 7 dimensiones “ocultas” o quizas mas
pues eso no es una teoria, solo una ipotesis. deberiamos tratar de acostumbrarnos a dar menos bombo a la palabra “teoria” ya que el mero hecho de que algo sea irrebatible no lo hace cierto. por mucho que toda teoria sea cierta mientras no se demuestre lo contrario.
si tenemos que inventarnos numeros para que cuadren las matematicas, quiza solo sea que no se midio bien de un principio
el 19 de enero del 2017 a las 6:53
Amigo mío:
No cabe la menor duda de que, muchas de las “teorías” que hoy salen a la luz, en realidad, no son más que conjeturas e hipótesis que deben ser comprobadas una y mil veces por científicos diferentes, en distintos lugares, y, desde luego bajo diversos métodos y, cuando todo eso ocurra y el resultado sea el mismo cada vez… ¡Será una Teoría! Mientras tanto, sólo sueños son.
Claro que, no debes perder de vista la imaginación que siempre ha demostrado tener la gente de nuestra especie. Podemos recordar que Thales de Mileto ya vió la importancia que tenía el agua para la vida, Empédocles atisbó la existencia de elementos (Agua, tierra, fuego y aire), y, el filósofo sonriente, Demócrito de Abdera, nos habló del a-tomo o átomo, la parte invisible e indestructible más pequeña de la materia, y, pasados algunos miles de años, ya vez hasta donde han llegado auquellas primeras ideas que, aunque “groseras” y poco pulidas ya apuntaban a algo mucho mayor.
Siempre estaremos lanzando conjeturas que, más tarde, serán o no serán pero, de todas esas ideas siempre algo queda y, algunas llegan a converger con la realidad de la Naturaleza, se hacen teorías que al ser comprobadas llegan a la categoría de leyes.
Sigamos especulando.
Un abrazo.