Oct
1
¿Teoría de Cuerdas? ¡Qué extraña resulta!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (2)
Comments (2)
Todos los que nos asomamos por la ventana de la Física, sabemos, más o menos que, después de más de treinta años de historia con la Teoría de dimensiones extra, no es aún, nada fácil encontrar una respuesta sencilla a una sencilla pregunta: ¿Qué es, la Teoría de Cuerdas? Y, lógicamente, muchos científicos del ámbito de la física, están verdaderamente escandalizados con todo este movimiento del que ellos, hablan como de un montaje circense, una comedia en la que, expertos malabaristas de las matemáticas topológicas, hacen trucos de magia para que parezca lo que no es.
Sin embargo, la cosa no parece que sea tan fácil de despachar, cientos y miles de artículos avalan esa Teoría que, en muchos aspectos, parece ser la esperanza futura de la Física y la única que nos puede abrir caminos ahora cerrados que, nos llevarán más lejos, a lugares que ahora, con la física actual, no podemos visitar.

Claro que no todo son críticas, en un artículo publicado en Ciencia Kanija nos dicen: “La teoría ha sido elogiada por algunos físicos debido a su potencial para forjar el largamente buscado vínculo entre la gravedad y las fuerzas que dominan en el núcleo atómico. Pero la teoría – que propone que todas las partículas subatómicas son en realidad diminutas “cuerdas” que vibran de diferentes formas – también ha arrastrado críticas por ser incomprobable en el laboratorio, y tal vez imposible de conectar con los fenómenos del mundo real.
Sin embargo, los investigadores de Princeton han descubierto una nueva prueba matemática de que alguna de las predicciones de la Teoría de Cuerdas se entrelazan estrechamente con un cuerpo de la física muy respetable llamado “Teoría Gauge”, el cual se ha demostrado que subyace en las interacciones entre quarks y gluones, los menudos objetos que se combinan para formar protones, neutrones y otras partículas subatómicas más exóticas. El descubrimiento, dicen los físicos, podría dar lugar a una gran cantidad de usos de la Teoría de Cuerdas atacando problemas de la física práctica.”

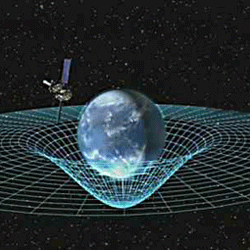
Es cierto que la Física está dominada por los paradigmas impuestos desde hace cien años por la mecánica cuántica y la relatividad que son dos teorías fundamentales que parten de principios rectores a partir de los cuales las teorías se construyen de una manera casi sistemática. En estos ejemplos es fácil de identificar ese principio rector:
En la Relatividad el principio es la constancia de la velocidad de la luz o, lo que es equivalente, que la velocidad de la luz determina una cota máxima sobre la velocidad de transmisión de información. Una vez aceptado este principio, el resto se da casi por añadidura. La constancia de la velocidad de la luz implica un espacio tiempo con una determinada geometría, la equivalencia entre masa y energía, así como el resto de los resultados de la Dinámica y la Cinemática Relativistas.
No podemos perder de vista el hecho cierto de que, la razón por la que la Relatividad se convierte en una auténtica Teoría autónoma es precisamente porque eleva la constancia de la velocidad de la luz a principio rector, a postulado. No se trata de explicar o modelar dinámicamente por qué la velocidad de la luz es la velocidad máxima sino que, muy por el contrario, se trata de derivar toda una cinemática, de hecho la propia naturaleza geométrica del espacio y el tiempo, a partir de dicho postulado.


El Universo de la Mecánica Cuántica nos es fantasmagórico e irreal, es un mundo aparte en el que, podemos ver cosas inusuales y sorprendentes, allí no rigen las mismas leyes que podemos constatar a nuestro alrededor en el mundo macroscópico, o, si están presentes, funcionan de otra manera que, alejada de nuestro propio mundo, no hemos llegado a comprender…del todo.
Nos decía el filósofo Karl Popper:
“La Ciencia será siempre una búsqueda, jamás un descubrimiento real. Es un viaje, nunca una llegada.”
El hombre llevaba toda la razón toda vez que, emprendemos la aventura de la Ciencia y tratamos de buscar “cosas” y “comportamientos” que nos digan por qué, la Naturaleza, funciona de esta o de aquella otra manera. Vamos desvelendo escenarios y obteniendo algunas respuestas pero, el viaje no acaba nunca, a cada puerta abierta, nos encontramos con otro nuevo espacio en el que también, existen muchas puertas cerradas cuyas llavez tendremos que encontrar y, siempre será, de esa manera: ¡Un viaje intermivnable!

Cada uno de estos cuatro espacios de Hilbert tiene un análisis de Fourier asociado con el.
L2([a,b]) → Series de Fourier
ℓ2([0,n−1]) → Transformada Discreta de Fourier
L2(R) → Transformada de Fourier
ℓ2(Z) → Transformada Discreta de Fourier en Tiempo
Pero los cuatros están basados en el mismo principio (Espacio de Hilbert).
Nota Importante:
no todos los espacios normalizados son espacios de Hilbert
El espacio de Hilbert es una pura construcción matemática pero responde a la perfección a lo que hacía falta para elaborar la teoría cuántica. De no haberse descubierto habría habido que inventarlo para las necesidades de la teoría. El espacio de Hilbert es un espacio vectorial infinitamente grande. En su momento, esto fue una idea revolucionaria, en virtud de que todos los espacios vectoriales, inclusive los espacios matemáticos abstractos, eran finitos. Pero afortunadamente en su trabajo sobre ecuaciones integrales llevado a cabo en 1912 David Hilbert tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Y quince años después correspondió a otro matemático igualmente brillante, el matemático húngaro John Neumann, el darle en 1927 una definición axiomática al espacio vectorial de Hilbert en su ya famosa obra Mathematische Grundlagen der Quantenmechanik. Pero Hilbert no solo propuso un espacio vectorial infinitamente grande. Propuso también que los componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores para que dicho producto pudiese seguir siendo un número real con significado físico.
En el caso de la Mecánica Cuántica el principio rector es el Principio de Incertidumbre de Heisenberg. De nuevo este principio se postula como principio básico y a partir de allí se deduce como tiene que ser el espacio de estados físicos, que se convierte en un espacio de naturaleza completamente nueva como lo es un espacio de Hilbert.
Esto da lugar a fenómenos tan sorprendentes como el entrelazamiento cuántico o la estabilidad atómica.

Sí, el camino ha sido largo. En la serie de artículos Fundamentos de una teoría general de las ecuaciones integrales, Hilbert analizó las técnicas introducidas para estudiar estas ecuaciones por Poincaré y Fredholm a finales del XIX, mejorando sus resultados. En el cuarto artículo de esta serie, publicado en 1906, Hilbert prueba que las ecuaciones integrales pueden resolverse como un sistema de infinitas ecuaciones lineales con infinitas incógnitas.

Todos los objetos situados en el mismo campo gravitatorio caen con la misma aceleración si y sólo si la proporción entre masa gravitacional e inercial es igual a una constante. Por eso precisamente decimos que, en Relatividad General, el principio rector es el principio de equivalencia entre masa inercial y masa gravitatoria.
En la Teoría de Cuerdas la situación es completamente distinta. Se desconoce cual pueda ser el principio rector, si en realidad existe algún principio rector en esta teoría, y es, precisamente este desconocimiento el qure genera en nosotros perplejidad cuando se nos pide una respuesta sencilla a: ¿Qué es la Teoría de Cuerdas?
Recordemos que el nacimiento de la teoría fue, esencialmente modesto. Aquel momento en el que proliferaban los experimentos de resonancias en interacciones fuertes con espines altos resultaba desconcertante, se observó que una manera de hacer consistente la mediación de la interacción con partícuals de espín alto consistía en imponer a las amplitudes de colisión una simetría particular que se denominó dualidad. Desde entonces las cosas han cambiado de manera exponencial y se habla de otra manera y de otras cosas. Veámos que nos dice, por ejemplo, uno de los padres de la teoría de cuerdas:
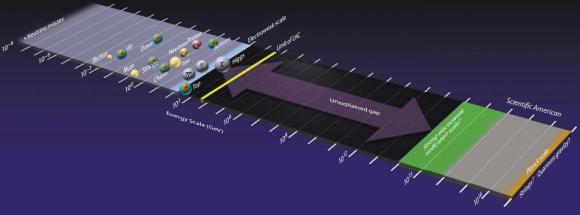
“Me gusta esta figura porque muestra muy claramente lo que conocemos en física de partículas, lo que esperamos explorar en las próximas décadas, y lo que creemos conocer, aunque nunca llegaremos a explorar de forma directa. La partícula con más masa conocida tiene menos de 200 GeV y todavía se sigue explorando entre 10 a 200 GeV en busca de nuevas partículas. Basta recordar que se acaba de descubrir una partícula con 125 GeV de masa, el bosón de Higgs, y que muchos físicos creen que la partícula responsable de la materia oscura tiene una masa en este rango. El LHC y sus sucesores en las próximas décadas explorarán las energías entre 100 y 5000 GeV (difícilmente podrán llegar más lejos). Sin embargo, hay un desierto hasta energías de 10 000 000 000 GeV (la escala de Planck) que no hemos explorado, que no podremos explorar en el siglo XXI y del que no conocemos absolutamente nada, aunque imaginamos muchas cosas.”
Como facilmente podemos deducir de lo que arriba se dice, estamos muy lejos aún de llegar a un autoconsistente final en la teoría de cuerdas que, posiblemente necesite disponer de la energía de Planck (1019 GeV), para verificarla de manera que no dejara ningún lugar a dudas. Hemos podido verificar la Teoría Cuántica y tambien, las dos versiones de la Teoría de la Relatividad. Sin embargo… Las cuerdas están lejos de ser una teoría que podamos aceptar y, sólo esperanzas podemos volcar en ella, con la idea de que, en un futuro más o menos lejano, nos pudiera dar aquellas respuestas que, de momento, no encontramos.

No podemos negar que algunos resultados en esta teoría han sido sobresalientes: Las resonancias, que habían actuado como motivación, se acomodaban como modos de vibración de las cuerdas y la democracia nuclear adquiría un status más sólido al reflejar una manera de unificar partículas, con espines arbitrariamente altos, como distintos modos de vibración de un mismo objeto fundamental. Aunque estos avances fueron destacados, la teoría empezó pronto a hacer aguas. En primer lugar, las cuerdas eran tan solo una manera de modelar la física subyacente a las amplitudes duales, pero por otra parte esta estructura de objetos extendidos fundamentales producía una serie de consecuencia que no iban a encajar con los futuros resultados experimentales en interacciones fuertes.

Las amplitudes duales, aunque implementaban la idea de democracia nuclear, daban ineludiblemente lugar a un comportamiento de las amplitudes a altas energías mucho más suave del que se observaba en la realidad. Por otro lado los avances formales habían mostrado que la consistencia de la teoría exigía un espacio tiempo de dimensión 26 y que el espectro contenía al menos un taquión (una partícula con masa imaginaria). Estos defectos fueron pronto, parcialmente subsanados, dando lugar a conceptos que han ocupado un papel crucial en la Física de los últimos lustros; estoy hablando de la supersimetría y al renacimiento de las ideas de Kaluza y Klein sobre espacio-tiempo con más de cuatro dimensiones.
Seguiremos hablando de la Teoría de Cuerdas y llegaremos hasta la actual posición que ocupa ésta compleja idea que algunos físicos han venido desarrollando en los últimos cuarenta años y que, nadie sabe en qué pueda desembocar. Muchas han sido las teorías que han sido desarrolladas y, siempre, nos dieron respuestas a cuestiones que, en un principio, ni podíamos imaginar.
¿Os acordáis de la Teoría del Caos?

El efecto mariposa, un atractor extraño
El orden lleva asociado un grado importante de predicción, al caos le sucede lo contrario. Los sistemas lineales, representan el orden, son predecibles y cómodos de manejar, de ahí nuestra tendencia a generalizarlos. Ante un sinfín de situaciones generalizamos, proyectamos los datos del presente para tratar de averiguar un comportamiento futuro y casi siempre nos va bien. Pero existen sistemas que se resisten: pequeñas variaciones, incertidumbres, en los datos iniciales desembocan en situaciones finales totalmente descontroladas e impredecibles. Son los llamados sistemas caóticos.
Pues, de la misma manera, estamos tratando de desarrollar una teoría que, de alguna manera, nos pueda responder a cuestiones que son presentidas e intuidas pero que, hasta el momento, nadie ha podido explicar y, es precisamente con la Teoría de Cuerdas con lo que se quiere buscar esas respuestas profundamente escondidas en las entrañas de la naturaleza: ¡La Teoría de Cuerdas! Que podría ser una quimera o una gran solución.
emilio silvera















 Totales: 75.386.559
Totales: 75.386.559 Conectados: 48
Conectados: 48

























el 3 de enero del 2015 a las 10:22
Las matemáticas en La Teoría de Cuerdas
el 4 de enero del 2015 a las 8:23
¡Hola, Domingo!
¿Querías decir alguna cosa?