Riemann y Euclides

La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas.

Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.

Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.

Pero volvamos al trabajo de Riemann. Su propósito era introducir un nuevo objeto en las matemáticas que le capacitase para describir todas las superficies, por complicadas que fueran. Ésto le condujo inevitablemente a reintroducir el concepto de campo de Faraday.

El campo de Faraday, recordémoslo, era como un campo de granjero que ocupa una región de un espacio bidimensional. El campo de Faraday ocupa una región de un espacio tridimensional; a cualquier punto del espacio le asignamos una colección de números que describe la fuerza eléctrica o magnética en dicho punto. La idea de Riemann consistía en introducir una colección de números en cada punto del espacio que descubriera cuánto estaba torcido o curvado.

Por ejemplo, para una superficie bidimensional ordinaria, Riemann introdujo una colección de tres números en cada punto que describe completamente la curvatura de dicha superficie. Riemann descubrió que en cuatro dimensiones espaciales se necesita una colección de diez números en cada punto del espacio para describir sus propiedades. Por muy retorcido o distorsionado que esté el espacio, esta colección de diez números en cada punto es suficiente para codificar toda la información sobre dicho espacio. Hoy, esta colección de números se denomina el Tensor métrico de Riemann.  Hablando crudamente, cuanto mayor es el valor del tensor métrico, mayor es el arrugamiento de la superficie, digamos de una hoja de papel, y el tensor métrico nos da un medio sencillo para medir la curvatura en cada punto.  Si alisamos completamente la hoja arrugada, entonces recuperamos la fórmula de Pitágoras.

El tensor métrico de Riemann le permitió erigir un potente aparato para describir espacios de cualquier dimensión con curvatura arbitraría. Para su sorpresa, encontró que todos estos espacios están bien definidos y son autoconsistentes. Previamente, se pensaba que aparecerían terribles contradicciones al investigar el mundo prohibido de dimensiones más altas. Riemann no encontró ninguna. De hecho, resultaba casi trivial extender su trabajo a un espacio N-dimensional. El tensor métrico se parecía ahora a un tablero de ajedrez de N x N casillas.

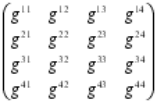
El tensor de Riemann contiene toda la información necesaria para poder describir un espacio curvo en N-dimensiones. Se necesita dieciséis números para describir el tensor métrico en un espacio tetradimensional. Estos números pueden disponerse en una matriz cuadrada (seis de dichos números son realmente redundantes; de modo que el tensor métrico tiene diez números independientes).

De hecho, en las nuevas teorías de supercuerdas, planteadas en diez y veintiséis dimensiones, tendríamos que hablar del supertensor métrico de Riemann y de cientos de componentes.

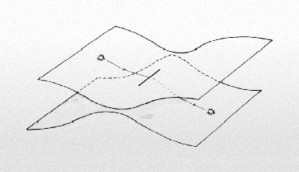
Gráfico: Un corte de Riemann, con dos hojas conectadas a lo largo de una línea.  Si caminamos alrededor del corte, permanecemos dentro del mismo espacio.  Pero si atravesamos el corte, pasamos de una hoja a la continua.  Esta es una superficie múltiplemente conexa

De la lección de Riemann se deduce que en espacios multidimensionales se crea el principio de que el espacio múltiple (de más dimensiones) unifica las leyes de la naturaleza encajándolas en el tensor métrico como piezas de un rompecabezas N-dimensional.

Riemann anticipó otro desarrollo de la física; fue uno de los primeros en discutir espacios múltiples y conexos, o agujeros de gusano.

Topológicamente hablando, el dibujo adjunto es equivalente a lo que sería un agujero de gusano con boca de entrada y de salida en regiones que nos llevarían a otro tiempo (así lo aseguró en 1.988, el físico Kip S. Thorne, del MIT ­- Instituto Tecnológico de Massachuse en California -).

El legado de Riemann (a pesar de su muerte prematura) fue extenso y en general muy valioso. En 1958, anunció incluso que finalmente había logrado una descripción unificada de la luz y la electricidad. Escribió: “Estoy completamente convencido de que mi teoría es la correcta, y de que en pocos años será reconocida como tal“. Aunque su tensor métrico le proporcionó un medio poderoso de describir cualquier espacio curvo en cualquier dimensión, él no conocía las ecuaciones exactas a que obedecía el tensor métrico; es decir, no sabía quçe es lo que hacía que la hoja se arrugase, eso lo vio seis décadas más tarde Einstein que se dio cuenta de que, en presencia de grandes masas, tales como planetas o estrellas – entre otros -, el espacio se “arruga” o “distorsiona”, se curva. Sin embargo Einstein sabía el origen de las arrugas y le faltaba el tensor métrico que, finalmente, le permitió legar al mundo su magnifica teoría.

El trabajo de Riemann, al utilizar el espacio multidimensional, logró simplificar las leyes de la naturaleza, es decir, para él, la electricidad y el magnetismo y también la gravedad eran simplemente los efectos causados por el arrugamiento o distorsión del hiperespacio.

Su asombroso trabajo (que no terminó), fue rematado por dos genios como Maxwell (electricidad y magnetismo) y Einstein (gravedad).

El mensajero de la cuarta dimensión, un pintoresco matemático inglés llamado Charles Howard Hinton que atravesó el Atlántico y la llevó a Norteamérica, formó bastante ruido a cuenta de la cuarta dimensión y se presentaba como experto en ella; tenía respuesta para cualquier pregunta.

Si le preguntaban ¿dónde está la cuarta dimensión?, su respuesta era invariable: “Está aquí, con nosotros, pero es tan pequeña que no la podemos ver“.

Básicamente, la respuesta de Hinton fue la misma que después dieron Kaluza y Klein para su quinta dimensión (la famosa teoría que unía el electromagnetismo de Maxwell y la gravedad de Einstein mediante la ocurrencia de elevar la teoría einsteniana en una dimensión más) y las que han dado otros físicos y matemáticos para explicar las teorías decadimensionales. En todas, cuando nació el tiempo y el espacio, en el Big Bang, resultó que tres dimensiones espaciales y una de tiempo se expandieron con el universo; las otras dimensiones se quedaron compactados en minúsculos círculos en la longitud de Planck, es decir una distancia de 10^-33 cm que se formula mediante ,  donde G,  es la constante gravitacional de Newton, ħ es la constante de Planck racionalizada, y c es la velocidad de la luz en el vacío. Esa es una distancia que, hoy por hoy, nuestros aparatos tecnológicos (microscópicos electrónicos, etc), no están capacitados para alcanzar.

Hay asuntos que en física, matemáticas o astronomía, están esperando una respuesta urgente.

emilio silvera

[?]