Algunos  creen que que Einstein sacó a la luz su relatividad especial, las leyes de Newton habían quedado olvidadas en un cuarto oscuro y, nada más lejos de la realidad. La física newtoniana siguen utilizándose ampliamente en la vida cotidiana, en la mayoría de los campos de la ciencia y en la mayor parte de la tecnología. No atención a la dilatación del tiempo cuando hacemos un viaje en avión, y los ingenieros no se preocupan  por la contracción de la longitud cuando diseña la nave. La dilatación y la contracción son demasiado pequeñas para que sean tomadas en consideración.

Por supuesto, podríamos utilizar, si quisoéramos, las leyes de Einstein  en lugar de las leyes de Newton en la vida de día. Las dos dan casi exactamente las mismas predicciones para todos los efectos físicos, puesto que la vida diaria implica velocidades relativas que son muy pequeñas comparadas con la velocidad de la luz.

Las predicciones de Einstein y Newton comienzan a diferir fuertemente sólo cuando las velocidades relativasd se aproximan a la velcoidad de la luz, Entonces, y sólo entonces debemos abandonar las predicciones de Newton y atenernos estrictamente a las de Eonstein. Este es un ejemplo de una pauta muy general. Es una pauta que se ha repetido una y otra vez a lo largo de la historia de la física del siglo XX: un conjunto de leyes (en este caso las leyes newtonianas) es ampliamente aceptado al principio, porque concuerda muy bien con el experimento.

Pero los experimentos vez se hacen más prcisos y este conjunto de leyes resultan funcionar bien sólo en un dominio limitado, su dominio de validez (para las leyes de Newton) el dominio de velocidades pequeñas comparadas con la velocidad de la luz en el vacío. Entonces los físicos se esfuerzan, experimental y teóricamente, para comprender qué está pasando en el límite de dicho dominio de validez, finalmente formulan un conjunto de leyes que es muy acertado dentro, cerca y más allá del límite (en el caso de Newton, la relatividad especial de Einstein, que sí es válida a velocidades próximas a las de la luz tanto a más bajas velocidades.

Hoy día, el mundo moderno de la física se funda notablemente en dos teorías principales, la realtividad general y la mecánica cuántica, aunque ambas teorías parecen contradecirse mutuamente. Los postulados que definen la teoría de la realtividad de Einstein y la teoría del quántum estan incuestionablemente apoyados por rigurosa y repetida evidencia empiríca. Sin embargo, ambas se resisten a ser incorporadas dentro de un mismo modelo coherente.

Nuevas maneras de sondear la Naturaleza y desvelar sus secretos están en marcha y, más adelante en el futuro, saldrán a la luz nuevas formas y nuefvas teorías que, entonces, sí que se podrán comprobar de manera experimental. Pero sigamos con la relatividad ede Einstein que, en su primera fase, la relatividad especial comienza a fracasar cuando se hace presente la Gravedad dde una manera importante, entonces, tiene que ser reemplazada por un conjunto de leyes que llamamos relatividad general; ésta fracasa en presencia de una singularidad interna de un agujero negro y, entonces, debe ser reemplazada por otro conjunto de leyes que conocemos como Gravedad Cuántica y que aún, no hemos podido dominar.

Einstein  nos decía que el espacio se curva en presencia de grandes masas

Lo cierto que es que, se ha dado una carqacterística sorprendente en cada transición de un viejo conjunto de leyes a otro : en casa caso, los físicos (si demostraban ser suficientemente inteligentes) no necesitaban ninguna guía experimental que les dijera dónde empezaría a fallar el viejo conjunto, es decir, que les indicara el límite de su dominio de validez. Ya hemos podido ver eso para la física newtoniana: las leyes de la electrodinámica de Maxwell no encajaban bien con el espacio absoluto de la física newtoniana. En reposo en el espacio absoluto (en aquel sistema del éter), las leyes de Maxwell eran simples y bellas -por ejemplo, las lineas de campo magnético no tienen extremo. En los sistmas en movimiento se vuelven complicadas y feas- las lineas de campo magnético tienen a vedces extremos. Sin embargo, las complicaciones tienen una influencia despreciable sobre el resultado de los experimentos cuando los sistmas se mueven., con relación al espacio absoluto, a velocidades pequeñas comparadasd con la de la luz; entonces casi nuinguna linea de campo tiene extremos. Sólo a velocidades que se aproximan a la de la luz era previsible que las feas complicaciones tuvierqan una influencia suficientemente grande como para ser medidas con facilidad: montenes de extremos. De este modo,  eera razonable sospechar, incluso en ausencia del experimento de Michelson-Morley, que el dominio de validez de la física newtoniana podría ser el de las velocidades pequeñas comparadas con la de la Luz, y que las leyes newtonianas podrían venirse abajo a velocidades cercanas a la de la luz.

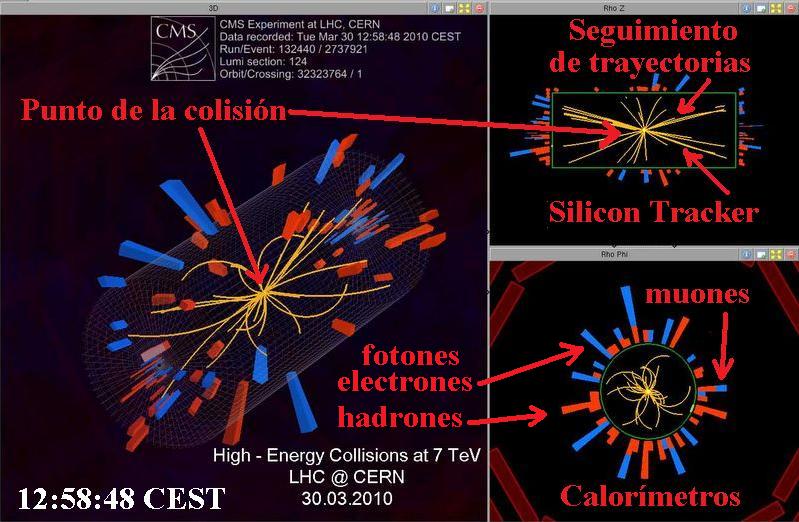
El LHC es un esfuerzo internacional, donde participan alrededor de siete mil físicos de 80 países. Consta de un túnel en de anillo, con dimensiones interiores parecidas a las del metro subterráneo de la Ciudad de México, y una circunferencia de 27 kilómetros. Está ubicado entre las fronteras de Francia y Suiza, cerca de la ciudad de Ginebra, a profundidades que van entre los 60 y los 120 metros debido a que una parte se encuentra bajo las montañas del Jura.

Claro que, hablando de lo quen nos ocupa, al contemplar la secuencia anterior de conjuntos de leyes (física newtoniana, relativisdata especial, relativista general, gravedad cuántica), y una secuencia similar de leyes que gobiernan la estructura de la materia y las partículas elementales, la mayoría de los físicos tienen a creer que estas secuencias están convergiendo un conjunto de leyes últimas que verdaderamente gobiernan el Universo, leyes que obligan al Universo a mostrarse como es y comportarse como nosotros vemos que lo hace, que obligan a la lluvia a condensarse en las cristaleras de las ventanas, obliga al Sol a quemar combistible nuclear convertir lo elemental y sencillo en más complejo que, más tasrde tendrá su función determinada, obliga a los agujeros negros a producir ondas gravitatorias cuando colisionan ellos, a que las estrellas masivas, al final de sus vidas explotan como supernovas para formar hermosas Nebulosas y conformar nuevos objetos masivos como púlsares, estrellas de neutrones y agujeros negros… Y, por eso…

¡La Gravedad! Siempre está presente e incide en los comportamientos de la materia

Todo esto ha podido ser comprendido con el paso del tiempo y a medida que se sumaban los descubrimientos y los pensamientos de unos y otros, y, por ejemplo, Einstein también concluyó que si un cuerpo pierde una energía L, su masa disminuye en L/c2. Einstein generalizó conclusión al importante postulado de que la masa de un cuerpo es una medida de su contenido en energía, de acuerdo con la ecuación m=E/c2 ( o la más popular E=mc2).

Otras de las conclusiones de la teoría de Einstein en su modelo especial, está en el hecho de que quien viaje a velocidades cercanas a c (la velocidad de la luz en el vacío), el tiempo transcurrirá más lento. Dicha afirmación también ha sido experimentalmente comprobada.

Todos estos conceptos, por nuevos y revolucionarios, no fueron aceptados por las buenas y en un primer , algunos físicos no estaban preparados para comprender cambios tan radicales que barrían de un plumazo, conceptos largamente arraigados.

      Todo lo grande está hecho de cosas pequeñas

Claro que, podríamos objetar que, cada conjunto de leyes en la secuencia “tiene un aspecto” muy diferente del conjunto precedente. (Por ejemplo, el tiempo absoluto de la física newtoniana tiene un aspecto muy diferente de los muchos flujos de tiempos diferentes de la relatividad especial.) ¿Por qué,  entonces, deberíamos esperar una convergencia? La respuesta es que hay que distinguir claramente entre las predicciones hechas a partir de un conjunto de leyes y las imágenes mentales que las leyes transmiten (lo que las leyes “aparentan”). Yo espero la convergencia en términos  de predicciones, pero esto es todo lo que finalmente . Las Imágenes mentales (un tiempo absoluto en la Física newtoniana frente a los muchos flujos de tiempo en la física relativista) no son importantes para la naturaleza última de la realidad.

Se podría objetar que cada conjunto de leyes en la secuencia, tiene su propio su aspecto y que, no tienen porque converger. El mismo conjunto de leyes de Newton tiene un aspecto muy diferente de los muchos flujos de tiempos diferentes de la relatividad especial. En los aspectos de las leyes no existe ningún de convergencia y, desde luego, las caracteristicas de cada conjunto de leyes, aunque sean diferentes,  no son importantes esas diferencias para el resulta último final de la realidad última a la que la Naturaleza quiere llegar.

Un agujero negro es lo definitivo en distorsión espaciotemporal, según las ecuaciones de Einstein: está hecho única y exclusivamente a partir de dicha distorsión. Su enorme distorsión está causada por una inmensa cantidad de energía compactada: energía que reside no en la materia, sino en la propia distorsión. La distorsión genera más distorsión sin la ayuda de la materia. Esta es la esencia del agujero negro.relatividad/”>

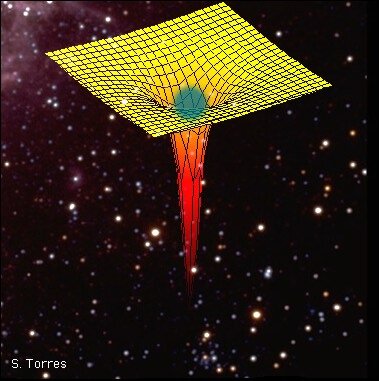
En cuanto a la distorsión del espacio y el tiempo, tenekos que Hermann Mynkowski unificaba el espacio y el Teimpo y Einstein lo distorsionaba.

“Las ideas de espacio u tiempo que deseo exponer ante ustedes han brotado del suelo de la física experimental, y en ello reside su fuerza. Son radicales. En lo sucesio, el espacio por sí mismo, y el tiempo por sí mismo, están condenados a desvanecerse en meras sombras, y sólo un de unión de ambos conservará una realidad independiente: ¡El Espaciotiempo!”

Con esas palabras proféticas Minkiwski reveló al mundo, en septiembre de 1908, un descuberimiento sobre la naturaleza del espacio y el tiempo. Einstein había demostrado que el espacio u el tiempo eran “relativos”. La longitud de un objeto y el flujo del tiempo eran diferentes cuando se miran diferentes sistemas de referencia.

Minkouski comprendió, de manera perfecta, la profundidad y el verdadero mendaje que la teoría de Eisntein llevaba consigo y, habiéndola entendido a la pefección, le expuso al mundo el nacimiento del espaciotiempo: Ambos, Tiempo y Espacio conformados como un todo.

Hay una historia (adaptada de Tauylor y Wheeler (1992) que ilusta la ideqa subyacente al descubrimiento de Minkowski pero, la dejaré para otra ocasión. El tema de las leyes de Newton, las dos versiones relativistas y la no hallada gravedad cuántica, nos daría para glunos abultados tomos que, no pueden ser escritos aquí

emilio silvera

La ciencia (del latín scientĭa ‘conocimiento‘) es el conjunto de conocimientos estructurados sistemáticamente. La ciencia es el conocimiento obtenido mediante la observación de patrones regulares, de razonamientos y de experimentación en ámbitos específicos, a partir de los cuales se generan preguntas, se construyen hipótesis, se deducen principios y se elaboran leyes generales y sistemas organizados por medio de un método científico. (Wikipedia)

Lo cierto es que la curiosidad del Ser Humano fue siempre la impulsora de que pudiéramos ir avanzando en el saber del mundo, de la Naturaleza, del Universo mismo. Siempre hemos buscado el cómo el cuando y el por qué de las cosas que podíanmos observar a nuestro alrededor sin comprenderlas. Ya desde los tiempos primitivos, nuestros ancestros, de alguna manera rústica, hicieron y dieron los primeros pasos en Ciencia, cuando llegaron a manejar el fuego o construyeron la rueda.

Cuando nos ponemos a hablar de Ciencia en relación a su historia y los orígenes de la misma, la mayoría de las veces nos perdemos por vericuetos que nos llevan hasta callejones sin salida situados muy lejos en el tiempo y que no podemos ver con claridad. Así las cosas, nos vemos obligados a ser menos ambiciosos y mirar más cerca poder obtener algunos resultados más fiables de lo que pudo pasar en esos pueblos del mundo que, como Sumer, India, Egipto, China y más tarde Grecia, nos dejaron una buena colección de señales del saber que pudieron llegar hasta nuestros días. De todo eso hemos hablado aquí en diversos  trabajos presentados.

Sin imaginación nunca habriamos avanzado

La ciencia y el pensamiento proceden de la necesidad de investigar, de indagar, y su fin es la investigación. Ésta nace de una insatisfacción frente a las respuestas que proporciona la tradición las preguntas fundamentales de la existencia humana y material. El fundamento de la primera ciencia de que se tiene noticia, la filosofía, consiste en que el hombre no posee las respuestas a las cuestiones que se le plantean, sino que debe buscarlas para alcanzar la sabiduría: no es “sophias” (sofía) o sabiduría en sí, sino “philosophia”, es decir, amor por la sabiduría, deseo de poseer la sabiduría, indagación directa para rastrear la verdad más allá de las costumbres, de las tradiciones y de las apariencias.

Se han realizado algunos estudios en los que, finalmente, se reconocía que entre el siglo IX y el siglo XV “el flujo de la ciencia y la tecnología entró en Europa sobre todo procedente del Islam”. Expertos de la Revista Sciencie informa de que las contribuciones del Islam y de China figuran entre los acontecimientos que “representan los innumerables giros, vueltas, paradojas, contradicciones, tragedias y otros detalles históricos deshilvanados que se han sintetizado en esa realidad mucho más compleja y variada que es la aventura científica”. Otros acontecimientos de este que figuran en la lista son la práctica de la Alquimia por parte de Newton, el falso descubrimiento de los “rayos N” y las negativas de los geólogos a aceptar la teoría de la deriva continental.

Nos quedamos con lo último pero… El origen está más lejos.

Por lo general, cuando oímos hablar de Isaac Newton nos vienen a la cabeza sus aportaciones a la ciencia, y en especial a la física y las matemáticas. Sin embargo, Newton no sólo fue uno de los más importantes científicos de todos los tiempos, sino que a lo largo de su vida dedicó gran de sus esfuerzos a cuestiones como la Alquimia o la teología, interesándose, por ejemplo, en descifrar lo que interpretó como un código oculto en la Biblia –lo que le llevó al estudio de la cábala hebrea–, o en intentar determinar el probable aspecto del Templo de Salomón, además de muchas otros intereses que hoy pueden resultarnos insólitos un científico.

No existe una buena definición de la Ciencia. Después de muchas tentativas, la American Physical Society, se decidió finalmente por una definición pero, consideraba que si la definición era muy larga, se podrían colar en ella alguna pseudociencias tales como ; si la hacían demasiado estricta, podrían quedar exclídos temas como la teoría de cuerdas, la biología evoluctiva e incluso la Astronomía.

Es una Ciencia por derecho propio, nos habla del Universo, del espacio-tiempo, de todo lo que existe y que está conformado por la materia y, de las fuerzas que lo rigen todo.

Así que definir lo que la Ciencia es, ser realistas, no es una tarea fácil si tenemos en su diversidad, su complejidad, su maravillosa y extensa estructura que hace un recorrido que abarca todo el saber del mundo y, sintetizar eso, en unas pocas palabras…aparte de ser una difícil tarea, tiene el peligro de no decir lo que pretende expresar. “La ciencia es un estudio lógico y sistemático de la naturaleza y del mundo físico que, generalmente incluye tanto experimento como teoría”. En verdad es una definición bastante floja. La Ciencia, eas mucho más que eso y, para esa incompletitud, mejor me quedaría con: “La Ciencia es la que nos lleva hacia la Sabiduría, hacia el conocimiento del “mundo”, del Universo y todo lo que en él está presente”.

En la primera definición (no la mía), el autor ha puesto generalmente en cursiva, y explica: “porque se planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recreqar nuevas estrellas o galaxias en el laboratorio, ni escenificar la formación del Sistema solar. Sin embargo, en astronomía las observaciones son a menudo tan valiosas como el experimento. El cometa Halley regresa con una regularidad sorprende; el Sol sale mañana”.

El Filósofo Kal Popper añadió el rerquisito de la “refutación”. La Ciencia es refutable; la religión no es. Una teoría o una ley científica munca pueden ser demostradas de una manera absoluta; de ahí que sea posible refutarlas. Por ejemplo, Newton dijo que la fuerza es igual al producto de la masa por la aceleración ( F= ma). No podemos demostrar que todos los objetos de todas las galaxias obedecen ley o que todos los objetos obedecerán siempre esta ley. Sin embargo, para demostrar la falsedad de esta ley bastaría un sólo experimento. (Albert Einstein y algunos expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos). Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal afirmó Popper. Estas teorías han de ser comprobables. No existe tal requisito en el caso de la religión.

Dicho esto, sigue habiendo problemas con la definición de lo que la Ciencia es. , por ejemplo, es refutable. Si un astrólogo nos dice que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse. Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría de todo”, requeriría un acelerador de partículas de diez años-luz de diámetro para poder refutarla. La mayor parte de la biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una nueva especie, ni recrear los dinosaurios comenzando con un animal unicelular. Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas y quizá incluso la astronomía.

En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la refutación de Popper. De otro modo, podríamos vernos obligados a excluir toda la ciencia de los antiguos griegos. Éstos no sólo eludían los experimentos, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.

Algo que no se debe tomar en considración es el pragmatismo de la ciencia o la motivación del científico. Estas cuestiones se han utilizado a menudo desacreditar las ciencias no occidentales:  sí,  es un bien hecho , pero no es “puro”; o, a la inversa, no resulta práctico. En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por motivos religiosos: los matemáticos árabes perfeccionaron el álgebra en para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas. En estos casos, la ciencia estuvo al servicio de la religión.

La ley de los opónimos de Stigler, formulada por el experto en estadística Stephen Stigler (arriba), afirma que ningún descubrimiento científico lleva el de su descubridor original. Él mismo admite que “su Ley”, en realidad, fue descubierta por Robert K. Merton, un especialista en sociología de la ciencia.

todos los casos en los que se cumple la Ley Stigler, el más famoso es el del Teorema de Pitágoras, según el cual la suma de los cuadrados de los dos lados perpendiculares de un triángulo rectángulo es igual al cuadrado de la hipotenusa de dicho triángulo. O bien en lenguaje matemático, a² + b² = c², donde a y b son los lados perpendiculares y c es la hipotenusa. Jacob Bronowski escribe lo siguiente:

“Hasta la , el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse a planetas de otros sistemas solares a modo de test, para comprobar si en estos planetas existe vida racional”.

Claro que, los hindúes, los egipcios y los babilonios utilizaban “tríos pitágóricos” determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. Pitágoras “inventó” su teorema hacia el año 550 a. C. Los babilonios habían catalogados cientos de tríos antes del año 2000 a. C., en una época en la que Pitágoras ni había nacido.

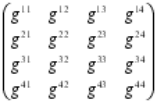
Lo mismo se podría decir de Riemann y Einstein, cuando éste último utilizó el Tensor métrico de aquel (formulado 60 años antes) poder formular su teoría de la relatividad general.

Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

                                                                 Los espacios curvos de Riemann

El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Eintein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la realtivdad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina relatividad general, y las ecuaciones de campo de Einstein se sitúan las ideas más profundas de la historia de la ciencia.

                                    Sí, dudas hemos tenido todos

Hay otras muchas cuestiones de las que podríamos hablar y, la Física y la Astronomía, siendo mi gran Pasión, ocupa mucho de mi tiempo

1. Una simetría unificadora.
2. La capacidad de explicar grandes cantidades de experimentales con las expresiones matemáticas más económicas.

El Modelo Estándar falla en ambos aspectos, mientras que la relatividad general los exhibe, ambos, de manera bien patente. Nunca una teoría dijo tanto con tan poco; su sencillez es asombrosa y su profundidad increíble.De hecho, que se publicó en 1.915, no ha dejado de dar frutas, y aún no se han obtenido de ella todos los mensajes que contiene.

El principio director del modelo estándar dicta que sus ecuaciones son simétricas. De igual modo que una esfera ofrece el mismo aspecto cualquier punto de vista, las ecuaciones del modelo estándar subsisten sin variación al cambiar la perspectiva desde la que son definidas. Las ecuaciones permanecen invariables, además, cuando esta perspectiva se desplaza en distinta magnitud a diferentes puntos del espacio y el tiempo.

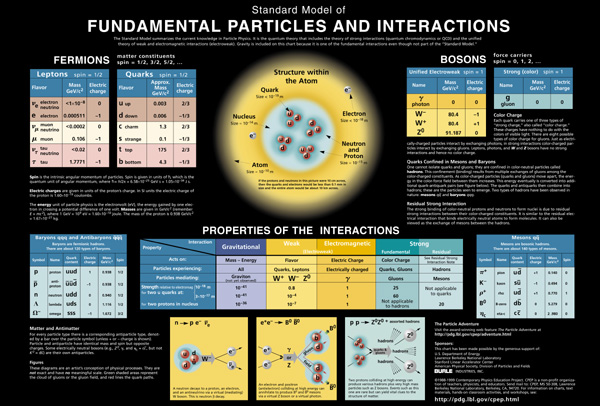
Al contrario de la relatividad general, la simetría del Modelo Estándar, está realmente formada empalmando tres simetrías más pequeñas, una por cada una de las fuerzas; el modelo es espeso e incómodo en su forma. Ciertamente no es económica en modo alguno. Por ejemplo, las ecuaciones de Einstein,  escritas en su totalidad, sólo ocupan unos centímetros y ni siquiera llenaría una línea de esta página. A partir de esta escasa línea de ecuaciones, podemos ir más allá de las leyes de Newton y derivar la distorsión del espacio, el Big Bang y otros fenómenos astronómicos importantes como los  Agujeros Negros.  Por el contrario, sólo escribir el Modelo Estándar en su totalidad requeriría, siendo escueto, un par de páginas  y parecería un galimatías de símbolos complejos sólo entendibles por expertos.

Claro que, todo esto es, otroa historia.

emilio silvera