Ene
6
El pensamiento asombroso: ¡Las ideas!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Ludwig Boltzmann será el protagonista de hoy
Hay ecuaciones que son aparentemente insignificantes por su reducido número de exponentes que, sin embargo, ¡dicen tántas cosas…! En la mente de todos están las sencillas ecuaciones de Einstein y de Planck sobre la energía-masa y la radiación de cuerpo negro. Esa es la belleza de la que hablan los físicos cuando se refieren a “ecuaciones bellas”.

Maxwell
 Las ecuaciones de Maxwell…, “y se hizo la luz”
Las ecuaciones de Maxwell…, “y se hizo la luz”
La identidad de Euler: Algunos dijeron de su ecuación: “la expresión matemática más profunda jamás escrita”, “misteriosa y sublime”, “llena de belleza cósmica”, “una explosión cerebral”.

Newton y su segunda ley que, aunque no funcione cuando nos acercamos a velocidades relativistas, rompió la marcha hacia la Gravedad.

Pitágoras y “su” teorema, también debe estar presente como lo está su teorema en las construcciones de todo el mundo y… mucho más.

Schrödinger y su función de onda que tampoco se queda atrás (aunque como la ecuación de Newton, si hablamos de velocidades relativistas…)

Bueno, E = mc2, nos lleva a profundidades de la materia antes jamás vistas y nos permite sacar conclusiones como que, en un gramo de materia está encerrada toda la energíaconsumida por la Humanidad durante un minuto. ¡Masa y Energía son la misma cosa! Einstein, con esa ecuación de arriba de la relatividad especial, vino a cambiar el mundo y, cuando quince años más tarde desarrolló la segunda parte, relatividad general, a partir de entonces, nació la verdadera cosmología. ¡Nos habla de tántas cosas!
¿Qué decir de la maravillosa fórmula de la entropía de Boltzman?
S = k log W
Creo que ahora, hablaremos de ella. Boltzman con su trabajo e ingenio, le dio a la Humanidad la herramienta para que pudiera seguir avanzando en el difícil laberinto de la Cienca, es, sin duda, uno de los físicos más ilustres del siglo XIX.
El trabajo científico desarrollado por Boltzmann en su época crítica de transición que puso el colofón a la física “clásica” –cuya culminación podríamos situar en Maxwell– y antecedió (en pocos años) a la “nueva” física, que podemos decir que comenzó con Max Planck y Einstein. Aunque ciertamente no de la importancia de los dos últimos, la labor científica de Boltzmann tiene una gran relevancia, tanto por sus aportaciones directas (creador junto con “su amigo” Maxwell y Gibbs de la mecánica estadística, aunque sea el formulismo de éste último el que finalmente haya prevalecido; esclarecedor del significado de la entropía, etc.) como por la considerable influencia que tuvo en ilustres físicos posteriores a los que sus trabajos dieron la inspiración, como es el caso de los dos mencionados, Planck y Einstein.
Cuando algo nos gusta y nos atrae, cuando es la curiosidad la que fluía nuestros deseos por saber sobre las cosas del mundo, del Universo y las fuerzas que lo rigen, cuando la Física se lleva dentro al poder reconocer que es el único camino que nos dará esas respuestas deseadas, entonces, amigos míos, los pasos te llevan a esos lugares que, por una u otra razón tienen y guardan los vestigios de aquellas cosas que quieres y admiras. Así me pasó cuando visité el Fermilab, la tumba de Hilbert y, también en Viena, donde no pude resistir la tentación de ver, con mis propios ojos esa imagen de arriba y, desde luego, pensar en lo mucho que significaba la escueta S = k log W que figura en la cabecera de la lápida de Boltzmann como reconocimiento a su ingenio.
La sencilla ecuación (como todas las que en Física han tenido una enorme importancia, es la mayor aportaciópn de Boltzmann y una de las ecuaciones más importantes de la Física. El significado de las tres letras que aparecen (aparte la notación para el logaritmo es el siguiente: S es la entropía de un Sistema; W el número de microestados posibles de sus partículas elementales y k una constante de proporcionalidad que hoy día recibe el nombre de constante de Boltzmann y cuyo valor es k = 1,3805 x 10-23 J(K (si el logaritmo se toma en base natural). En esta breve ecuación se encierra la conexión entre el micromundo y el macromundo, y por ella se reconoce a Boltzmann como el padre de la rama de la Física comocida como Mecánica Estadistica.

La entropía de un sistema es el desgaste que el sistema presenta por el transcurso del tiempo o por el funcionamiento del mismo. Los sistemas altamente entrópicos tienden a desaparecer por el desgaste generado por su proceso sistémico. Es una medida de desorden o incertidumbre de un sistema.
Como todas las ecuaciones sencillas de gran trascendencia en la física, hay un antes y un después de su formulación: sus consecuencias son de un calado tan profundo que han cambiado la forma de entender el mundo y, en particular, de hacer Física, a partir de ellas.De hecho, en este caso al menos, la sutileza de la ecuación es tal que hoy, más de cien años después de la muerte de su creador, se siguen investigando sus nada triviales consecuencias.

Boltzmann fue un defensor a ultranza del atomismo, polemizando sobre todo con Mach y Ostwald, antiatomistas partidarios de la energética y claros exponentes de la corriente idealista de la física alemana. Tuvo que abandonar su ambiciosa idea de explicar exactamente la irreversibilidad en términos estrictamente mecánicos; pero esta “derrota”, no ocultaré que dolorosa desde el punto de vista personal, le fue finalmente muy productiva, pues de alguna manera fue lo que le llevó al concepto probabilista de la entropía. Estas primeras ideas de Boltzmann fueron reivindicadas y extendidas, en el contexto de la teoría de los sistemas dinámicos inestables, sobre todo por la escuela de Prigogine, a partir de la década de 1970.
La personalidad de Boltzmann era bastante compleja. Su estado de ánimo podía pasar de un desbordante optimismo al más negro pesimismo en cuestión de unas pocas horas. Era muy inquieto; él decía – medio en serio, medio en broma – que eso se debía a haber nacido en las bulliciosas horas finales de los alegres bailes del Martes de Carnaval, previas a los “duelos y quebrantos” (entonces) del Miércoles de Ceniza.

Boltzmann at age 31 with his wife, Henrietta, in 1875
Su lamentable final, su suicidio en Duino (Trieste) el 5 de septiembre de 1906, muy probablemente no fue ajeno a esa retorcida personalidad, aunque su precaria salud física fue seguramente determinante a la hora de dar el trágico paso hacia el lado oscuro.
Uno de los problemas conceptuales más importantes de la física es cómo hacer compatible la evolución irreversible de los sistemas macroscópicos (el segundo principio de la termodinámica) con la mecánica reversible (las ecuaciones de Hamilton o la ecuación de Schrödinger) de las partículas (átomos o moléculas) que las constituyen. Desde que Boltzmann dedujo su ecuación en 1872, este problema ha dado lugar a muy amplios debates, y el origen de la irreversibilidad es, aún hoy en día, controvertido.
En una de sus primeras publicaciones, Boltzmann obtuvo en 1866 una expresión de la entropía, que había sido definida un año antes por Clausius, basado en conceptos mecánicos. Las limitaciones de este trabajo eran que su aplicación se restringía al estudio de los gases y que el sistema era periódico en el tiempo. Además, Boltzmann no pudo deducir de su definición de entropía la irreversibilidad del segundo principio de la termodinámica de Clausius. En 1868, basándose en las ideas probabilísticas de Maxwell, obtuvo la distribución de equilibrio de un gas de partículas puntuales bajo la acción de una fuerza que deriva de un potencial (distribución de Maxwell-Boltzmann).

En el Universo, considerado como sistema cerrado, la entropía crece y…
En 1.872 publicó la denominada ecuación de Boltzmann para cuya deducción se basó, aparentemente, en ideas mecánicas. Esta ecuación contiene, sin embargo, una hipótesis no mecánica (estadística) o hipótesis del caos molecular, que Boltzmann no apreció como tal, y cuya mayor consecuencia es que, cualquiera que sea la distribución inicial de velocidad de un gas homogéneo diluido fuera del equilibrio, ésta evoluciona irreversiblemente hacia la distribución de velocidad de Maxwell. A raíz de las críticas de Loschmidt (paradoja de la reversibilidad) y Zermelo (paradoja de la recurrencia), Boltzmann acabó reconociendo el carácter estadístico de su hipótesis, y en 1877 propuso una relación entre la entropía S de un sistema de energía constante y el número de estados dinámicos W accesibles al sistema en su espacio de fases; esto es, la conocida ecuación S = kB ln W, donde kB es la constante de Boltzmann. En esta nota, se hace una breve descripción de la ecuación de Boltzmann y de la hipótesis del caos molecular.

El comportamiento de los gases siempre dio a los físicos en qué pensar
La ecuación de Boltzmann describe la evolución temporal de un gas diluido de N partículas puntuales de masa m contenidas en un volumen V que interaccionan a través de un potencial de par central repulsivo V(r) de corto alcance a. Como simplificación adicional, considérese que sobre las partículas no actúan campos externos. Si f1(r,v,t) indica la densidad de partículas que en el tiempo t tienen un vector de posición r y velocidad v, que está normalizada en forma:
∫dr ∫dvƒ1(r,v,t) = N
Su evolución temporal es la suma de dos contribuciones. En ausencia de interacción, las partículas que en el tiempo t tienen vector de posición r y velocidad v se encuentran, después de un intervalo de tiempo Δt, en r + v Δt y tiene la misma velocidad. Como
f1(r + vΔt,v,t + Δt) = f1(r,v,t)
en el límite Δt → 0 (2) se escribe:
∂1 f1(r,v,t) = – v∂r f1(r,v,t)
Que es una ecuación invariante bajo el cambio t → – t y v → – v. La evolución es, por tanto, mecánica.

Se cumplieron más de cien años desde la muerte de Boltzmann y su trabajo sigue siendo recordado. No pienso que Boltzmann creyera en la existencia real de los átomos, pero sí en su utilidad e incluso en su necesidad para comprender las leyes macroscópicas y la evolución irreversible de los fenómenos macroscópicos desde una base más fundamental que el nivel fenomenológico. Pero había quien (con autoridad) no creía ni en la existencia ni en su utilidad. Este debate no era ajeno a las tendencias ideológicas, religiosas y usos sociales de aquella época porque, en general, la ciencia es parte de la cultura y depende del momento histórico que viven los científicos, al fin y al cabo, seres humanos como los demás, influenciables por su entorno en una gran medida.
Por el siglo XIX, e incluso antes, ya se hablaba de “átomos”* y una rudimentaria teoría cinética de los gases gozaba de aceptación y utilidad científica (recordemos los trabajos de Benoulli, Dalton, Laplace, Poisson, Cauchy, Clausius, Krönig… y Maxwell). Pero fue Boltzmann quien definitivamente profundizó en la cuestión, para el estudio del equilibrio y, sobre todo, intentando explicar mecánicamente (mecano-estadísticamente) la evolución termodinámica irreversible y la descripción de los procesos de transporte ligados a ella. Y, nuevamente (por su enorme importancia) no podemos dejar de mencionar la muy singular labor que hicieron Gibbs, Einstein, Planck, Fermi y otros. Sin la motivación ideológica de Boltzmann, Gibbs elaboró una bellísima, útil y hoy dominante formulación (cuerpo de doctrina) de la termodinámica y física estadística.
Lorentz
Fue Lorentz quien primero utilizó la ecuación de Boltzmann y lo hizo para describir la corriente eléctrica en sólidos dando un paso significativo por encima del pionero Drude. Lorentz introdujo un modelo opuesto al browniano donde partículas ligeras como viento (electrones) se mueven chocando entre sí y con árboles gordos (tales como iones en una red cristalina); un modelo del que se han hecho estudios de interés tanto físico como matemático. Enskog (inspirándose en Hilbert) y Chapman (inspirándose en Maxwell) enseñaron cómo integrar la ecuación de Boltzmann, abriendo vías a otras diversas aplicaciones (hidrodinámica, propagación del sonido, difusión másica, calor, fricción viscosa, termoelectricidad, etc.). Recordemos que Boltzmann encontró como solución de equilibrio de su ecuación una distribución de velocidades antes descubierta por Maxwell (hoy, como reseñé anteriormente, de Maxwell-Boltzmann), por lo que concluyó que así daba base microscópica mecánica (teorema H mecano-estadístico) al segundo principio de la termodinámica (estrictamente, evolución de un sistema aislado hacia su “desorden” máximo).
Está claro que ningún físico que se precie de serlo puede visitar Viena sin visitar el parque Zentralfriedhof para ver la tumba de Boltzmann. Yo sí me pasé por allí. Me senté junto a la tumba; el lugar estaba desierto, y cerrando los ojos traté de conectar con la conciencia del genio. La sensación, extraña y agradable, seguramente fue creada por mi imaginación, pero creo que charlé con él en el interior de mi mente – la fuerza más potente del universo– y aquellos sentimientos, aquel momento, compensaron el esfuerzo del viaje.
En la tumba, sobre una gran lápida de mármol de color blanco con los nombres Ludwig Boltzmann y de los familiares enterrados con él, sobre el busto de Boltzmann, se puede leer la inscripción, a modo de epitafio:
Esta sencilla ecuación es la mayor aportación de Boltzmann y una de las ecuaciones más importantes de la física. El significado de las tres letras que aparecen (aparte la notación del logaritmo) es el siguiente:
- S es la entropía de un sistema.
- W es el número de microestados posibles de sus partículas elementales.
- k es una constante de proporcionalidad que hoy recibe el nombre de Constante de Boltzmann, de valor 1’3805 × 10-23 J/K (si el logaritmo se toma en la base natural)

¿Qué secretos se encierran aquí? ¿Cómo nos lleva a estos pensamientos?
En esta breve ecuación se encierra la conexión entre el micromundo y el macromundo, y por ella se reconoce a Boltzmann como el padre de la rama de la física conocida como mecánica estadística.
Como todas las ecuaciones sencilla de gran trascendencia en la física (como la famosa E = mc2), hay un antes y un después de su formulación: sus consecuencias son de un calado tan profundo que cambiaron la forma de entender el mundo, y en particular, de hacer física a partir de ellas. De hecho, la sutileza de la ecuación es tal que hoy, cien años después de la muerte de su creador, se siguen investigando sus nada triviales consecuencias. Creo que lo mismo ocurrirá con α = 2πe2/ħc que, en tan reducido espacio y con tan pocos símbolos, encierra los misterios del electromagnetismo (el electrón), de la constante de Planck (la mecánica cuántica), y de la luz (la relatividad de Einstein), todo ello enterrado profundamente en las entrañas de un número: 137.
Bueno, a pesar de todo lo anterior, Schrödinger nos decía:
“La actitud científica ha de ser reconstruida, la ciencia ha de rehacerse de nuevo”

¡Lo grande y lo pequeño! ¡Son tantos los secretos de la Naturaleza!
Siempre hemos tenido consciencia de que en física, había que buscar nuevos paradigmas, nuevos caminos que nos llevaran más lejos. Es bien conocida la anécdota de que a finales del siglo XIX un destacado físico de la época William Thomson (1824-1907) conocido como Lord Kelvin, se atrevió a decir que solo dos pequeñas “nubecillas” arrojaban sombras sobre el majestuoso panorama de conocimiento que había construido la física clásica desde Galileo y Newton hasta ese momento: el resultado del experimento de Michelson-Morley, el cual había fallado en detectar la existencia del supuesto éter luminífero; y la radiación del cuerpo negro, i.e la incapacidad de la teoría electromagnética clásica de predecir la distribución de la energía radiante emitida a diferentes frecuencias emitidas por un radiador idealizado llamado cuerpo negro. Lo que Lord Kelvin no puedo predecir es que al tratar de disipar esas dos “nubecillas”, la física se vería irremediablemente arrastrada a una nueva física: la física moderna fundada sobre dos revoluciones en ciernes: la revolución relativista y la revolución cuántica con dos científicos como protagonistas: Planck y Albert Einstein. Sin embargo, ha pasado un siglo y seguimos con esas dos únicas guías para continuar el camino y, resultan insuficientes para llegar a la meta que… ¡Está tan lejos!
emilio silvera
Ene
6
Moléculas vivas sorprendentes
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Biologia ~
Clasificado en Biologia ~
 Comments (1)
Comments (1)
En matemáticas se pueden trazar líneas precisas y concretas que dividan en dos clases entes de naturaleza matemática. Una estructura geométrica se puede suporponer o no a su imagen especular. Una estructura asimétrica puede tener una lateralidad a la derecha o bien a la izquierda.
Cualquier número entero positivo es par o impar, y no hay ninguno de tales números para el cual su situación a este respecto ofrezca la menor duda. Pero en el mundo, si exceptuamos el nivel subatómico de la teoría cuántica, las lineas divisortias son casi siempre difusas. El alquitrán, ¿es sólido o líquido?. Lo cierto es que, la mayoría de las propiedades físicas se “mueven” en un espectro continuo que hace que vayan cambiando de manera imperceptible de un extremo a otro del mismo.

El paso del tiempo convierte en líquido, gas o sólido algunos materiales y, a otros, los deforma hasta perder su estructura original para convertirmos en lo que antes no eran. Nada permanece, todo cambia. Sea cual fuere la línea de división, habrá algunos casos en los que no podamos definirla y, en otros, habrá objetos tan próximos a ella que el lenguaje ordinario no será lo suficientemente preciso como para poder afirmar a qué lado pertenece. Y, la propiedad de la vida, está, precisamente, en uno de esos continuos.
Para porbar esto basta que consideremos los virus: son las estructuras biológicas más pequeñas que se conocen con la propiedad de poder “comer” (absorber sustancias situadas en sus proximidades), crecer y fabricar copias exactas de sí mismas.
Son mucho más pequeños que una bacteria (en realidad, algunos virus infectan las bacterias) y pasan sin dificultad a través de un filtro de porcelana fina que, aunque a nosotros nos parezca que está completamente sellada y su superficie es totalmente hermética y lisa, para ellos, tan “infinitamente” pequeños, ofrece miles de huecos por los que poder colarse.
Nuevas grabaciones en vídeo de un virus que infecta a las células sugiere que los virus se expanden mucho más rápido de lo que pensábamos. El descubrimiento de este mecanismo permitirá crear nuevos fármacos para hacer frente a algunos virus. En la punta de un alfiler caben millones de ellos. De hecho, los virus tienen el tamaño de una décima de micrómetro (diezmillonésima parte del metro).
El mundo de lo muy pequeño es fascinante y, por ejemplo, si hablamos de átomos, se necesitarían aproximadamente una cantidad para nosotros inconmensurable de átomos (602.300.000.000.000.000.000.000) para lograr un solo gramo de materia. Fijáos que hablamos de lo pequeño que pueden llegar a ser los virus y, sin embargo, el Hidrógeno con un sólo protón es el átomo más ligero y su masa es 400.000 veces menor que la masa de un virus, como antes dije, el organismo vivo más pequelo que se conoce. El virus más diminuto conocido mide unos o,00000002 m; su tamaño es 2.000 veces mayor que el del átomo. Y, en la punta del algiler que antes mencionamos cabrían 60.000.000.000 (sesenta mil millones) de átomos.

Como los virus son menores que la longitud de onda de la luz, no pueden observarse con un microscopio luminoso ordinario, pero los bioquímicos disponen de métodos ingeniosos que les permiten deducir su estructura, ya que pueden verlos mediante bombardeos con rayos X u otras partículas elementales.
En ralidad, se puede decir que un cristal “crece”, pero lo hace de un modo ciertamente trivial. Cuando se encuentra en una solución que contiene un compuesto semejante a él, dicho compuesto se irá depositando sobre su superficie; a medida que esto ocurre, el cristal se va haciendo mayor, pero el virus, igual que todos los seres vivos, crece de una manera más asombrosa: toma elementos de su entorno, los sintetiza en compuestos que no están presentes en el mismo y hace que se combinen unos con otros de tal manera que lleguen a dar una estructura compleja, réplica del propio virus.

(imagen modificada de: “Diagnostic Microbiology” – Bailey & Scotts)
Los virus sólo se multiplican en células vivientes. La célula huésped debe proporcionar la energía y la maquinaria de síntesis, también los precursores de bajo peso molecular para la síntesis de las proteínas virales y de los ácidos nucleicos. El ácido nucleico viral transporta la especificidad genética para cifrar todas las macromoléculas específicas virales en una forma altamente organizada.

El poder que tienen los virus de infectar, e incluso matar, un organismo, se debe precisamente a esto. Invade las células del organismo anfitrión, detiene su funcionamiento y lo sustituye, por decirlo de alguna manera, por otros nuevos. Ordena a la célula que deje de hacer lo que normalmente hace para que comience a fabricar las sustancias necesarias para crear copias de sí mismo, es decir, del virus invasor.
El primer virus que se descubrió, y uno de los más estudiados, es el virus sencillo que produce la “enfermedad del mosaico” en la planta del tabaco. Cristaliza en forma de barras finas que pueden observarse a través del microsopio electrónico. Recientemente se ha descubierto que cada barra es, en realidad, una estructura helicoidal orientada a la derecha, formada por unas 2.000 moléculas idénticas de proteína, cada una de las cuales contiene más de 150 subunidades de aminoácidos.

Ene
5
Los Genes marcan lo que somos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Biologia ~
Clasificado en Biologia ~
 Comments (0)
Comments (0)
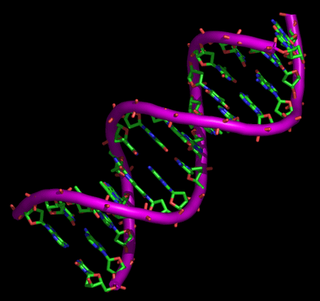
Existen “claves” que son diagramas , trazados a escala, de cuatro moléculas (bases del nucleótido) cuya excepcional interrelación interna, inserta bajo la cremallera del ácido desoxirribonucleico (ADN), contiene el código de toda la vida en la Tierra. Se ha llegado a explicar con precisión cómo miles de características únicas, que varían de un individuo a otro, se tramsmiten intactas de generación en generación. Este descubrimiento fue el prtogreso más grande del siglo XX en el campo del conocimiento biológico.

Situación del ADN dentro de una célula
En el interior de cada célula de nuestro cuerpo tenemos cadenas de ADN increíblemente largas. Es la materia prima de los genes. Almacena, reproduce y transmite todas nuestras características personales y únicas, nuestra herencia genética. Estas cadenas de ADN contienen las plantillas codificadas de las proteínas, que son los ladrillos de nuestros cuerpos.
Esta codificación es una serie de combinaciones de cuatro moléculas llamadas bases de los nucleótidos (y representadas por las letras A, G, C y T), que dan todas las instrucciones necesarias para fabricar nuestro cuerpo. Heredamos ADN de nuestros dos progenitores y, puesto que recibimos una mezcla única de ambos, la cadena de ADN de cada uno de nosotros es ligeramente distinta de la de los demás. Nuestro ADN es como una huella dactilar molecular.


Durante la reproducción sexual humana, el ADN de los progenitores se copia y se transmite en proporciones iguales. Es importante saber que, aunque casi todo el ADN de cada progenitor se separa durante la reproducción, en cada generación se barajan y se mezclan pequeños fragmentos de las dos aportaciones. Por mezcla no se entiende la distribución aleatoria y masiva, sino pequeños intercambios, duplicaciones y permutas entre el lote materno y el lote paterno de ADN. Este fenómeno se llama técnicamente “recombinación”. Afortunadamente para los fines de los investigadores genéticos, hay dos pequeñas porciones de nuestro ADN que no se recombinan. El ADN no recombinante es más fácil de rastrear, dado que su información no se altera durante su transmisión de una generación a otra. Las dos pequeñas porciones son el ADN mitocondrial (ADNmt) y la parte no recombinante del cromosoma Y (YNR).
Así que, el ADN mitocondrial es útil para el estudio evolutivo, en primer lugar, porque su variabilidad depende exclusivamente de las mutaciones, ya que no sufre el ya mencionado proceso de recombinación durante la concepción. En segundo lugar, permite un seguimiento de la línea materna evolutiva, pero solamente se podría estudiar en zonas que se saben estuvieron habitadas por mujeres, por lo que poría traer fallas, en caso de que la población femenina fuera mayor a la masculina. Aquellas regiones donde el ADN m. presnetan mayor variabilidad, significaran que allí se han producido mayores mutaciones en el tiempo, por tanto serán más antigua, rastreándose así nuestra posible zona de origen. El número de genes en el ADN mitocondrial es de 37, frente a los 20.000 – 25.000 genes del ADN cromosómico nuclear humano.
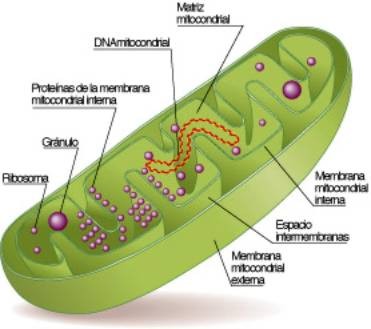
Así que, decir que recibimos el 50% de nuestro ADN de nuestro padre y el otro 50% de nuestra madre no es totalmente verdadero. Un pequeño fragmento de nuestro ADN se hereda sólo a través de la madre. Es al que antes nos referíamos como el ADN mitocondrial porque se trata de filamentos circulares individuales contenidos en pequeñas cápsulas tubulares llamadas mitocondrias que funcionan un poco como baterias en el interior del citoplasma celular.

Algunos biólogos moleculares dicen que, cuando el mundo era joven, la mitocondria era un organismo autónomo con su propio ADN y poseía el secreto de generar muchísima energía. Invadió organismos unicelulares nucleados y allí sigue desde entonces, dividiéndose, como la levadura, por fusión binaria. Aunque los varones reciben y usan el ADN mitocondrial de la madre, no pueden transmitirlo a los hijos. El esperma tiene mitocondrias propias para propulsar el largo viaje desde la vagina hasta el óvulo, pero al entrar en éste, las mitocondrias masculinas se marchitan y se mueren.

Así pues, cada cual hereda el ADNmt de la madre, quer a su vez lo ha heredado intacto de su madre y ésta de la suya, hasta el infinito; de ahí que el nombre popular del ADNmt, “el gen EVA”. En última instancia, todas las personas que viven hoy en el mundo han heredado su ADN mitocondrial de una única antepasada que vivió hace casi 200.000 años. Este ADNmt nos proporciona un raro punto de estabilidad en las arenas movedizas de la transmisión del ADN. Sin embargo, si todos los cromosomas EVA del mundo actual fueran una reproducción exacta del primer gen Eva, todos serían idénticos. Sería algo prodigioso, pero significaría que el ADNmt tiene poco que decirnos sobre nuestra prehistoria. Saber que todas las mujeres descienden de una remota EVA común resulta emocionante, pero no nos ayuda a reconstruir la vida de cada una de sus hijas. Necesitamos un poco de variedad.
Los genes pueden mutar (transformarse) de diferentes formas. La forma más sencilla de mutación implica un cambio en una base individual a lo largo de la secuencia de bases de un gen en particular–muy parecido a un error tipográfico en una palabra que ha sido mal escrita. En otros casos, se pueden agregar o eliminar una o más bases. Y algunas veces, grandes segmentos de una molécula de ADN se repiten, se eliminan o se traslocan accidentalmente.
Así, aparecen mutaciones puntuales del ADN. Al heredar el ADNmt de nuestra madre, a veces hay un cambio en una o más “letras” del código del ADNmt, aproximadamente una mutación cada mil generaciones. La nueva letra, llamada “mutación puntual”, se transmitirá desde entonces a todas las descendientes. Aunque otra mutación es un fenómeno raro dentro de una sóla línea familiar, la probabilidad total de las mutaciones aumenta de manera visible a causa de la cantidad de mujeres que tienen hijas. Así, en una generación, un millón de mujeres podrían tener más de mil hijas con una mutación personal e intransferible. Por este motivo, y salvo que hayamos tenido una antepasada común en los últimos 10.000 años, cada cual tiene un código que es ligeramente distinto del de los demás.

Sí, aunque pequeñas, existen esas probabilidades de mutaciones del genéticas
Claro que, también existe el “Gen Adán”. A semejanza del ADNmt de transmisión materna y que reside fuera del núcleo de la célula, dentro del núcleo hay un paquete de genes que sólo se transmite por línea masculina. Es el cromosoma Y, el cromosoma definidor de la masculinidad. Exceptuiando un pequeño segmento, el cromosoma Y no desempeña ningún papel en el promiscuo intercambio de ADN que se permiten otros cromososmas, esto significa que, al igual que el ADNmt, la parter no recombinable del cromosoma Y pasa intacta a cada generación y puede ser rastreado, siguiendo una linea ininterrumpida, hasta nuestro primer antepasado masculino.
Los cromosomas Y se utilizan desde hace menos tiempo que el ADNmt en la reconstrucción de árboles genéticos y existen problemas para estimar el alcance cronológico. Cuando se solucionen, el método YNR podría tener una resolución cronológica y geográfica mucho mayor que el ADNmt, tanto para el pasado reciente como para el remoto. Esto se debe sencillamente a que el YNR es mucho mayor que el ADNmt y en consecuencia tiene mayor viabilidad potencial.
Bueno, tanto este artículo, o, pasaje (de una parte de nosotros) como el del día anterior que llamé: Estamos señalados por muchos dones pero…¡El habla!, nos viene a confirmar que, la vida, no es sólo “la materia evolucionada”. ¡La Vida! es mucho más que todo eso y, seguramente, como nos dice el amigo Kike, sea una parte sustancial del Universo que, a través de su sabia Naturaleza, nos ha creado para poder contemplarse (también lo decía Nelson) como nos dijo el sabio.
emilio silvera
Fuente: Los Senderos del Edén de Stephen Oppeheimer.
Ene
5
El sorprendente Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo asombroso ~
Clasificado en El Universo asombroso ~
 Comments (0)
Comments (0)

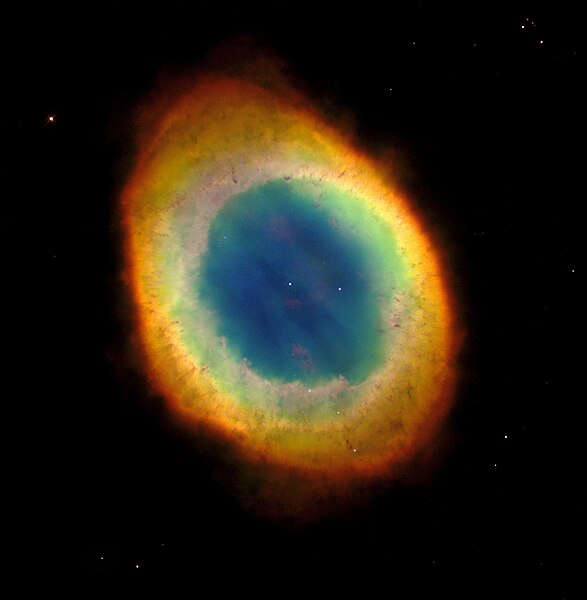
Aquí tenemos a la Nebulosa del Huevo, una nebulosa protoplanetaria en la costellación de Cygnus
La nebulosa del huevo es una nebulosa protoplanetaria que fue identificada en 1975 por un grupo de investigación del Observatorio Palomar, esta nebulosidad de reflexión asociada a una simétrica fuente altamente polarizada fue identificada como una posible nebulosa planetaria muy joven.
Aparece formado por una serie de círculos concéntricos de luz alrededor de la estrella central, una densa capa de gas y polvo se extiende alrededor de la estrella, bloqueando sus rayos en nuestra dirección. Sin embargo, la luz llega a nosotros de una manera indirecta por la reflexión de la nube de gas. Los polvos tienen un interior oscuro se ve como un disco; chorros bipolares fuera de la nube de indicar que el sistema tiene un momento angular, probablemente generada por un disco de acreción.

Nosotros empleamos el término de nebulosa protoplanetaria para la etapa temprana de la formación de una nebulosa planetaria. En esta fase, la estrella central ha expulsado sus capas exteriores, dajando al caliente núcleo estelar expuesto. La luz ultravioleta del núcleo comienza a ionizar la nube de gas y polvo circundante, y durante una breve fase la envoltura circunestelar contiene a la vez material ionizado y muy caliente cerca de la estrella y material molecular frío lejos de la misma.

Identificados discos protoplanetarios en la Nebulosa de Orión
Cuanto hablamos de nebulosa protoplanetaria, también nos estamos refiriendo a la nube a partir de la cual se forman los planetas alrededor de una estrella recien nacida , como ocurrió en nuestra propia nebulosa solar. En estas inmensas nebulosas se forman remolinos creados por la gravedad al juntarse una ingente cantidad de gas y polvo que rota y atrae más material que en el centro se va compromiendo hasta llegar al punto de generar tanta temperatura que se forma una protoestrella a punto de comenzar la fusión del hifrógeno en helio. El material que expulsa esa futura estrella es lanzado a diferentes distancias y, como el material de la propia estrella, también está girando. Cuando se enfrían, se convierten en planetas que orbitan al cuerpo principal: La estrella nueva que ha formado así, su propio sistema planetario.


En repetidas ocasiones hemos tenido aquí las imágenes de nebulosas planetarias de muy distintas figuras, son una familia muy rica por su diversidad y extraña belleza. Arriba podemos contemplar el halo de la Nebulosa conocida con el nombre Ojo de gato, y, abajo, la Nebulosa en sí misma que conforma una imagen muy pecular de volutas de gases que nos hablan de las distintas eyecciones de la estrella central al expulsar sus capas exteriopres al espacio interestelar.
Como nuestro Sol en el futuro será una de estas bellas nebulosas, me extenderé un poco más en explicarlas. Hablamos de una brillante nube de gas y polvo luminoso que rodea a una estrella altamente evolucionada en los últimos instantes de su larga vida de 10.000 millones de años. Una Nebulosa planetaria se forma cuando una gigante roja (que es el destino del Sol dentro unos 4.000 millones de años), arroja sus capas exteriores al espacio a una velocidad de unos diez kilómetros por segundo.

Cada estrella en función de sus masas, tienen marcado sus destinos

Decíamos que al llegar a la fase de gigante roja, el Sol expulsará sus capas exteriores que formaran una envoltura alrededor de la estrella y, ese gas, en las cercanías del núcleo será ionizado por la inmensa radiación ultravioleta que irradia la estrella que ha alcanzado temperaturas muy grandes. A medida que pierde materia, el núcleo queda progresivamente expuesto hasta convertirse en una estrella enana blanca. Las nebulosas planetarias suelen tener típicamente un diámetro de unos o,5 años-luz.

Otro ejemplo de Nebulosa planetaria con la enana blanca expuesta a la vista
Este tipo de Nebulosas son muy brillantes debido a la altísima temperatura del núcleo que, como he dicho antes, ioniza todo el material que la circunda. La Nebulosa planetaria dura unos 100.000 años, tiempo durante el cual una fracción apreciable de la masa de la estrella es devuelta al espacio interestelar. Gracias a los modernos telescopios hemos podido captar una gran variedad de este tipo de nebulosas que cubren una amplia gama de tipos diferentes, incluyendo las que tienen forma de anillo.
La de arriba es la Nebulosa Planetaria conocida como del Anillo
Los procesos que siguen al final de la vida de las estrellas están supeditados a sus masas. Una estrella con la masa de nuestro Sol, cuando consume todo su combustible nuclear de fusión, se resiste a morir y se convierte en una Gigante roja que, termina (como hemos dicho) expulsando sus capas exteriores al espacio para crear una nebulosa planetaria y convertirse en una estrella enana blanca. Es decir, para convertirse en una pequeña y densa estrella que es el resultado de la evolución de todas las estrellas excepto de las más masivas.

Para que os hagáis una idea de como se compactará la masa del Sol cuando se convierta en una enana blanca, ahí tenéis una imagen a escala de lo que sería en relación al planeta Tierra. Sabemos que el Sol tiene un diámetro de 1 392 530 Km, que el de la Tierra es de 12 756 Km. Sin embargo, cuando el Sol se conviertew en una enana blanca, tendrá un diámetro muy similar al de la Tierra como consecuencia de su inemnsa densidad (5 x 108 Kg/m3).
Al finalizar la intensa radiación que producía la fusión en el núcleo de la estrella y que la hacía expandirse para quedar sujeta por la fuerza de gravedad que tendía a contraerla, las estrellas como el Sol, después de convertirse dn gigantes rojas y soltar parte de su masa al espacio, quedan a merced de la fuerza gravitatoria que generan sus propias masas, lo que da lugar a que comiencen a contraerse sobre sí mismas más y más.
Llegados a este punto no tenemos más remedio que recordar aquí al físico W. Pauli que vaticinó la existencia de un principio de exclusión para los fermiones que, según la mecánica cuántica, dos partículas nunca podrían ocupar el mismo lugar por no permitirlo un principio de exclusión al que dieron su nombre. Es decir, para partículas idénticas en un sistema, como por ejemplo los electrones, no pueden estar muy juntos y se repelen de manera violenta. Así, cuando la Gravedad comprime la masa de la estrella y los electrones se ven cada más juntos, llega un momento en el cual se sienten enclaustrados y se produce lo que se llama degeneración de los electrones que, en ese momento, comienzan a moverse con velocidades relativistas, hasta tal punto que son capaces de detener a la fiuerza gravitatoria que los comprime y, de esa manera, se estabiliza la estrella enana blanca y queda frenada la contracción gravitacional.
La temperatura inicial, con el paso del tiempo se va enfriando gradualmente, volviéndose más débiles y rojas. Las enanas blancas pueden constituir el 30% de la vecindad solar, aunque debido a sus bajas luminosidadesde unas 10-3/10-4 veces la del Sol pasan inadvertidas. La masa máxima posible para una enana blanca es de 1,44 masas solares, el límite de Chandrasekhar. Un objeto de masa mayor se contraería aún más para convertirse en estrella de neutrones (al degenerarse los neutrones en lugar de los electrones que no pueden detener esa inmensa gravedad), o, si la masa de la estrella es muy alta, sigue contrayéndose hasta convertirse en un Agujero Negro.
También existen las enanas negras, marrones y rojas pero… ¡Esas son otras historias!
emilio silvera
Ene
4
¿Podría ser el valor de G decreciente?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Lo que creemos que sabemos ~
Clasificado en Lo que creemos que sabemos ~
 Comments (0)
Comments (0)
La fuerza gravitatoria que se produce en presencia de masas… ¡No parece variar!
Nadie ha sabido responder a la pregunta de si las constantes de la naturaleza son realmente constantes o llegará un momento en que comience su transformación. Hay que tener en cuenta que para nosotros, la escala del tiempo que podríamos considerar muy grande, en la escala de tiempo del universo podría ser ínfima. El universo, por lo que sabemos, tiene 13.700 millones de años. Antes que nosotros, el reinado sobre el planeta correspondía a los dinosaurios, amos y señores durante 150 millones de años, hace ahora de ello 65 millones de años. Mucho después, hace apenas 2 millones de años, aparecieron nuestros antepasados directos que, después de una serie de cambios evolutivos desembocó en lo que somos hoy.

Mucho tiempo ha pasado desde que esta imagen era el presente, y, sin embargo, para el Universo supone una ínfima fracción marcada por el Tic Tac cósmico de las estrellas y galaxias que conforman la materia de la que provenimos. Es un gran misterio para nosotros que sean las estrellas las que fabrican los materiales que, más tarde, llegan a conformar a seres vivos que, en algunos caso, tienen consciencia.
“La ciencia no puede resolver el misterio final de la Naturaleza. Y esto se debe a que, en el último análisis, nosotros somos parte del misterio que estamos tratando de resolver”.
Max Planck
De acuerdo con su perspectiva universal, en 1.899 Planck propuso que se construyeran unidades naturales de masa, longitud y tiempo a partir de las constantes más fundamentales de la naturaleza: la constante de gravitación G, la velocidad de la luz c y la constante de acción h, que ahora lleva el nombre de Planck. La constante de Planck determina la mínima unidad de cambio posible en que pueda alterarse la energía, y que llamó “cuanto”. Las unidades de Planck son las únicas combinaciones de dichas constantes que pueden formarse en dimensiones de masa, longitud, tiempo y temperatura. Se conocen como las Unidades de Planck.

Planck con sus unidades nos llevo al extremo de lo pequeño
| Mp = | (hc/G)½ = | 5’56 × 10-5 gramos |
| Lp = | (Gh/c3) ½ = | 4’13 × 10-33 centímetros |
| Tp = | (Gh/c5) ½ = | 1’38 × 10-43 segundos |
| Temp.p = | K-1 (hc5/G) ½ = | 3’5 × 1032 ºKelvin |
Estas formulaciones con la masa, la longitud, el tiempo y la temperatura de Planck incorporan la G (constante de gravitación), la h (la constante de Planck) y la c, la velocidad de la luz. La de la temperatura incorpora además, la K de los grados Kelvin.
“Estas cantidades conservarán su significado natural mientras la Ley de Gravitación y la de Propagación de la luz en el vacío y los dos principios de la termodinámica sigan siendo válidos; por lo tanto, siempre deben encontrarse iguales cuando sean medidas por las inteligencias más diversas con los métodos más diversos.”

Planck, en sus palabras finales alude a la idea de observadores en otro lugar del universo que definen y entienden estas cantidades de la misma manera que nosotros, ya que, al ser números naturales que no inventaron los hombres, todos los seres inteligentes del Universo tendrían que hallar el mismo resultado. No importa en qué planeta pudieran habitar, si son seres inteligentes, empleando los grafos más extraños que a nosotros nada nos pudiera decir, lo cierto es que hay un lenguaje universal: ¡Las matemáticas! que, independientemente de los guarismos empleados, al final de todo 2 x 5 = 10 y 2 + 2 + 2 + 2 + = 10. Empleen las ecuaciones o fórmulas que puedan con los números que puedan utilizar, no podrán variar los resultados de los números puros y adimensionales creados por la Naturaleza: Esas constantes que persisten en el tiempo y nunca cambian y que hacen de nuestro universo el que podemos observar, además de hacer posible la vida. A esos extraterrestres, también, la constante de estructura fina le daría 1/137.
“La creciente distancia entre la imagen del mundo físico y el mundo de los sentidos no significa otra cosa que una aproximación progresiva al mundo real.” Nos decía Planck. Su intuición le llevaba a comprender que, con el paso del tiempo, nosotros estaríamos adquiriendo por medio de pequeñas mutaciones, más amplitud en nuestros sentidos, de manera tal que, sin que nos diéramos cuenta nos estábamos acercando más y más al mundo real.

Una de las paradojas de nuestro estudio del universo circundante es que a medida que las descripciones de su funcionamiento se hacen más precisas y acertadas, también se alejan cada vez más de toda la experiencia humana.Nuestros sentidos nos traicionan y nos hacen ver, a través de nuestras mentes, un mundo distinto al real, es decir, nosotros configuramos nuestra propia “realidad” de esa otra realidad verdadera que está presente en la Naturaleza y que no siempre podemos contemplar y, cuando llegamos a contemplarla, no llegamos a comprenderla… del todo.
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.

Grandes cúmulos de galaxias
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Extraños mundos que pudieran ser
Después llegó Dirac (el que predijo la existencia del positrón) y, por una serie de números y teorías propuestas Eddintong en aquellos tiempos, decidió abandonar la constancia de la constante de gravitación de Newton, G. Sugirió que estaba decreciendo en proporción directa a la edad del universo en escalas de tiempo cósmicas. Es decir, la Gravedad en el pasado era mucho más potente y se debilitaba con el paso del tiempo.
Así pues, en el pasado G era mayor y en el futuro será menor que lo que mide hoy. Ahora veremos que la enorme magnitud de los tres grandes números (1040, 1080 y 10120) es una consecuencia de la gran edad del universo: todas aumentan con el paso del tiempo.
La propuesta de Dirac provocó un revuelo entre un grupo de científicos vociferantes que inundaron las páginas de las revistas especializadas de cartas y artículos a favor y en contra. Dirac, mientras tanto, mantenía su calma y sus tranquilas costumbres, pero escribió sobre su creencia en los grandes números cuya importancia encerraba la comprensión del universo con palabras que podrían haber sido de Eddington, pues reflejan muy estrechamente la filosofía de la fracasada “teoría fundamental”.

“¿No cabría la posibilidad de que todos los grandes sucesos presentes correspondan a propiedades de este Gran Número [1040] y, generalizando aún más, que la historia entera del universo corresponda a propiedades de la serie entera de los números naturales…? Hay así una posibilidad de que el viejo sueño de los filósofos de conectar la naturaleza con las propiedades de los números enteros se realice algún día”.
La propuesta de Dirac levantó controversias entre los físicos, y Edward Teller en 1.948, demostró que si en el pasado la gravedad hubiera sido como dice Dirac, la emisión de la energía del Sol habría cambiado y la Tierra habría estado mucho más caliente en el pasado de lo que se suponía normalmente, los océanos habrían estado hirviendo en la era precámbrica, hace doscientos o trescientos millones de años, y la vida tal como la conocemos no habría sobrevivido, pese a que la evidencia geológica entonces disponible demostraba que la vida había existido hace al menos quinientos millones de años.
George Gamow

Edward Teller
El eufórico George Gamow era buen amigo de Teller y respondió al problema del océano hirviente sugiriendo que podía paliarse si se suponía que las coincidencias propuestas por Dirac eran debidas a una variación temporal en e, la carga del electrón, con e2 aumentando con el tiempo como requiere la ecuación.
Por desgracia, la propuesta de Gamow de una e variable tenía todo tipo de consecuencias inaceptables para la vida sobre la Tierra. Pronto se advirtió que la sugerencia de Gamow hubiera dado como resultado que el Sol habría agotado hace tiempo todo su combustible nuclear, no estaría brillando hoy si e2 crece en proporción a la edad del universo. Su valor en el pasado demasiado pequeño habría impedido que se formaran estrellas como el Sol. Las consecuencias de haber comprimido antes su combustible nuclear, el hidrógeno, hubiera sido la de convertirse primero en gigante roja y después en enana blanca y, por el camino, en el proceso, los mares y océanos de la Tierra se habrían evaporado y la vida habría desaparecido de la faz del planeta.
Gamow tuvo varias discusiones con Dirac sobre estas variantes de su hipótesis de G variable. Dirac dio una interesante respuesta a Gamow con respecto a su idea de la carga del electrón, y con ello la constante de estructura fina, pudiera estar variando.
Recordando sin duda la creencia inicial de Eddington en que la constante de estructura fina era un número racional, escribe a Gamow en 1.961 hablándole de las consecuencias cosmológicas de su variación con el logaritmo de la edad del universo.
“Es difícil formular cualquier teoría firme sobre las etapas primitivas del universo porque no sabemos si hc/e2 es constante o varía proporcionalmente a log(t). Si hc/e2 fuera un entero tendría que ser una constante, pero los experimentadores dicen ahora que no es un entero, de modo que bien podría estar variando. Si realmente varía, la química de las etapas primitivas sería completamente diferente, y la radiactividad también estaría afectada. Cuando empecé a trabajar sobre la gravedad esperaba encontrar alguna conexión entre ella y los neutrinos, pero esto ha fracasado.”
En mecánica cuántica, el comportamiento de un electrón en un átomo se describe por un orbital, que es una distribución de probabilidad más que una órbita. En la figura, el sombreado indica la probabilidad relativa de «encontrar» el electrón en este punto cuando se tiene la energía correspondiente a los números cuánticos dados. Pensemos que si la carga del electrón variara, aunque sólo fuese una diezmillonésima parte, los átomos no se podrían constituir, las moléculas consecuentemente tampoco y, por ende, ni la materia… ¡Tampoco nosotros estaríamos aquí! ¡Es tan importante el electrón!
Dirac no iba a suscribir una e variable fácilmente, como solución al problema de los grandes números. Precisamente, su trabajo científico más importante había hecho comprensible la estructura de los átomos y el comportamiento del electrón, y dijo que existía el positrón. Todo ello basado en la hipótesis, compartida por casi todos, de que e era una verdadera constante, la misma en todo tiempo y todo lugar en el universo, un electrón y su carga negativa eran exactas en la Tierra y en el más alejado planeta de la más alejada estrella de la galaxia Andrómeda. Así que Gamow pronto abandonó la teoría de la e variable y concluyo que:
“El valor de e se mantiene en pie como el Peñón de Gibraltar durante los últimos 6×109 años.”

El Peñón de Gibraltar, tan familiar e inamovible como decía Dirac
Pero lo que está claro es que, como ocurre siempre en ciencia, la propuesta de Dirac levantó una gran controversia que llevó a cientos de físicos a realizar pruebas y buscar más a fondo en el problema, lo que dio lugar a nuevos detalles importantes sobre el tema.
Alain Turing, pionero de la criptografía, estaba fascinado por la idea de la gravedad variable de Dirac, y especuló sobre la posibilidad de probar la idea a partir de la evidencia fósil, preguntando si “un paleontólogo podría decir, a partir de la huella de un animal extinto, si su peso era el que se suponía”.
El gran biólogo J.B.S. Haldane se sintió también atraído por las posibles consecuencias biológicas de las teorías cosmológicas en que las “constantes” tradicionales cambian con el paso del tiempo o donde los procesos gravitatorios se despliegan de acuerdo con un reloj cósmico diferente del de los procesos atómicos (¿será precisamente por eso que la relatividad general – el cosmos –, no se lleva bien con la mecánica cuántica – el átomo –?).
Tales universos de dos tiempos habían sido propuestos por Milne y fueron las primeras sugerencias de que G podría no ser constante. Unos procesos, como la desintegración radiactiva o los ritmos de interacción molecular, podrían ser constantes sobre una escala de tiempo pero significativamente variables con respecto a la otra. Esto daba lugar a un escenario en el que la bioquímica que sustentaba la vida sólo se hacía posible después de una particular época cósmica, Haldane sugiere que:

“Hubo, de hecho, un momento en el que se hizo posible por primera vez vida de cualquier tipo, y las formas superiores de vida sólo pueden haberse hecho posibles en una fecha posterior. Análogamente, un cambio en las propiedades de la materia puede explicar algunas de las peculiaridades de la geología precámbrica.”
Este imaginativo escenario no es diferente del que ahora se conoce como “equilibrio interrumpido”, en el que la evolución ocurre en una sucesión discontinua de brotes acelerados entre los que se intercalan largos periodos de cambio lento. Sin embargo, Haldane ofrece una explicación para los cambios.

Lo que tienen en común todas estas respuestas a las ideas de Eddington y Dirac es una apreciación creciente de que las constantes de la naturaleza desempeñan un papel cosmológico vital:
Existe un lazo entre la estructura del universo en conjunto y las condiciones locales internas que se necesitan para que la vida se desarrolle y persista. Si las constantes tradicionales varían, entonces las teorías astronómicas tienen grandes consecuencias para la biología, la geología y la propia vida.
No podemos descartar la idea ni abandonar la posibilidad de que algunas “constantes” tradicionales de la naturaleza pudieran estar variando muy lentamente durante el transcurso de los miles de millones de años de la historia del universo. Es comprensible por tanto el interés por los grandes números que incluyen las constantes de la naturaleza. Recordemos que Newton nos trajo su teoría de la Gravedad Universal, que más tarde mejora Einstein y que, no sería extraño, en el futuro mejorará algún otro con una nueva teoría más completa y ambiciosa que explique lo grande (el cosmos) y lo pequeño (el átomo), las partículas (la materia) y la energía por interacción de las cuatro fuerzas fundamentales.
¿Será la teoría de Supercuerdas ese futuro?
emilio silvera
















 Totales: 75.005.148
Totales: 75.005.148 Conectados: 1
Conectados: 1