« ¡El Universo y la Vida!

No sería descabellado decir  que las simetrías que vemos a nuestro alrededor, un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia. Por ejemplo, la fuerza de Gravedad generada por la presencia de la materia, determina la geometría del espacio-tiempo.

Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física.  De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

                         Geometría → teoría de campos → teoría clásica → teoría cuántica.

Contrariamente, la teoría de supercuerdas ha evolucionando hacia atrás desde su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.

La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.

Función beta. Representación de la función valores reales positivos de x e y.

Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de descubrir, prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.

Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.

            Gabriele Veneziano es un físico italiano          Mahiko Suzuki

En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, la teoría de cuerdas fue descubierta hacia atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades. El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.

    Así, Witten dice:

“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos c del siglo XX no deberían haber tenido el privilegio de estudiar teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”

 

Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.

Ni con colección de llaves podremos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la Teoría M, la más moderna versión de la cuerdas expuesta por E. Witten y que, según contaron los que estuvieron presentes en su presentación, Witten les introdujo en un “universo” fascinante de inmensa belleza que, sin embargo, no puede ser verificado por el experimento.

El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de esta teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

¿Por qué diez dimensiones?

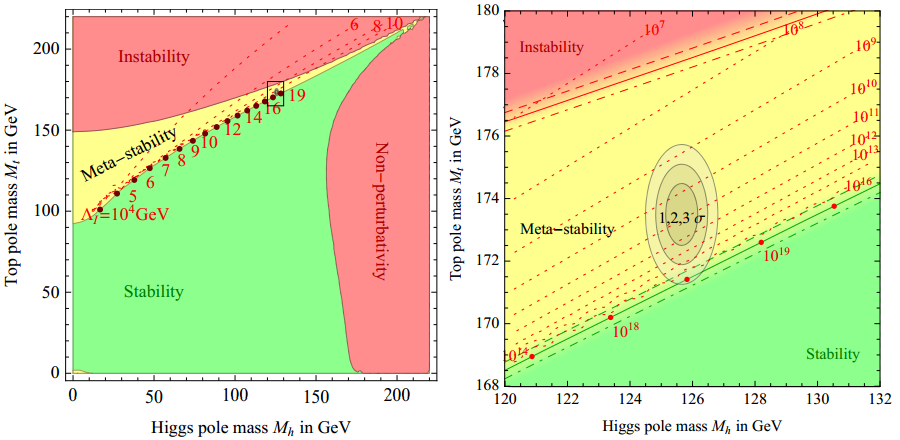
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un número único, el diez.

Por desgracia, los teóricos de cuerdas están, por el , completamente perdidos para explicar por qué se discriminan las diez dimensiones.  La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.

Al manipular los diagramas de lazos1 de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

nos asomamos a la Teoría de cuerdas, entramos en un “mundo” lleno de sombras en los que podemos ver brillar, a lo lejos, un resplandor cegador. Todos los físicos coinciden en el hecho de que es una teoría muy prometedora y de la que parece se podrán obtener buenos rendimientos en el futuro pero, de momento, es imposible verificarla.

El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió de cumplir cuarenta años, y como Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.

Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

       La magia esconde una realidad

El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende.   Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas.  En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista A_µ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell.  Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones.  Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.

               Godfrey Harold Hardy

G. H. Hardy, el mentor de Ramanujan,  trató de estimar la capacidad matemática que poseía Ramanujan.   Concedió a David Hilbert, universalmente conocido y reconocido uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80.   A Ramanujan le asignó una puntuación de 100.  Así mismo, Hardy se concedió un 25.

Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando diluvio material brotaba de sus sueños con semejante frecuencia.   Hardy señaló:

“Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena día, de nuevos teoremas”.

 

           Ramanujan

Hardy recordaba vivamente:

-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney.  Yo había tomado el taxi 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”

– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.

(Es la suma de 1 x 1 x 1  y 12 x 12 x 12, y la suma de 9 x 9 x 9  y  10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.

En 1.919 volvió a casa, en la India, donde un año más tarde murió  enfermo.

El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración.  En 1.976, sin embargo, se hizo un nuevo descubrimiento.   Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage.   Esto se conoce ahora con el de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:

“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”.  Lo que él consiguió era increíble.  Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.

 

Por mi creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna,   la única capaz de unir la mecánica quántica y la Gravedad.

   Fórmula de Ramanujan determinar los decimales de pi

Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie.   Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro.   Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.

saben los físicos, los “accidentes” no aparecen sin ninguna razón.  Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente.  Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego.  Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

                           Nuestro mundo asimétrico hermosas simetrias

Aquí es precisamente donde entra el trabajo de Ramanujan.  Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan.  ¡Increíble!   , cierto.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan su punto más débil.  Cualquier teoría, afirman, debe ser verificable.   Puesto que ninguna teoría definida a la energía de Planck de 10¹⁹ miles de millones de eV es verificable, ¡La teoría de cuerdas no es realmente una teoría!

El principal problema, es teórico más que experimental.  Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría.  Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

Volviendo a Ramanujan…

Es innegable lo sorprendente de su historia, un muchacho pobre con escasa preparación y arraigado pocos a sus creencias y tradiciones, es considerado como una de los mayores genios de las matemáticas del siglo XX. Su legado a la teoría de números, a la teoría de las funciones theta y a las series hipergeométricas, además de ser invaluable aún sigue estudiándose por muchos prominentes matemáticos de todo el mundo. Una de sus fórmulas más famosas es

utilizada realizar aproximaciones del número Pi con más de dos millones de cifras decimales. Otra de las sorprendentes fórmulas descubiertas por Ramanujan es un igualdad en que era “casi” un entero (la diferencia era de milmillonésimas). De hecho, durante un tiempo se llegó a sospechar que el número era efectivamente entero. No lo es, pero este hallazgo sirvió de base para la teoría de los “Cuasi enteros”. A veces nos tenemos que sorprender al comprobar hasta donde puede llegar la mente humana que, prácticamente de “la nada”, es capaz de sondear los misterios de la Naturaleza para dejarlos al descubierto ante nuestros asombros ojos que, se abren como platos ante tales maravillas.

Publica: emilio silvera

”Algunas personas buscan un significado a la vida a través del beneficio , a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida”.

Me refiero al Modelo estándar y, algunos han llegado a creer que sólo faltan algunos detalles técnicos y, con ellos, la física teórica está acabada. Tenemos un modelo que engloba todo lo que deseamos saber acerca de nuestro mundo físico. ¿Qué más podemos querer?

Bueno, lo que hasta el hemos logrado no está mal del todo pero, no llega, ni con mucho, a la perfección que la Naturaleza refleja y que nosotros perseguimos,  sin llegar a poder agarrar sus múltiples entrecijos y parámetros que conforman ese todo en el que, sin niguna clase de excusas, todo debe encajar y, de momento, no es así.

Es cierto que, el Modelo estándar es casi (en algunos momentos), pero no permanentemente, perfecto. En primer lugar, podríamos empezar a quejarnos de las casi veinte constantes que no se pueden calcular. Pero si esta fuese la única queja, habría poco que hacer. luego, se han sugerido numerosas ideas para explicar el origen de estos números y se han propuesto varias teorías para “predecir” sus valores. El problema con todas estas teorías es que los argumentos que dan nunca llegan a ser convincentes.

¿Por qué se iba a preocupar la Naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental , tal como el proncipio de la relatividad, pero nos resistimos a abandonar todos los demás principios que ya conocemos; ¡esos, después de todo, han sido enormemente útiles en el descubrimiento del Modelo estándar! una herramienta que ha posibilitado a todos los físicos del mundo, construir sus trabajos en ese fascinante mundo de la mecánica cuántica, donde partículas infinitesimales interactúan con las fuerzas y podemos ver, como se comporta la materia en determinadas circunstancias. El mejor lugar buscar nuevos principios es precisamente donde se encuentran los puntos débiles de la presente teoría.

La regla universal en la física de partículas es que cuando las partículas chocan con energías cada vez mayores, los efectos de las colisiones están determinados por estructurtas cada vez menores, más pequeñas en el espacio y en el tiempo. Supongamos por un momento que tenemos a nuestra disposición un Acelerador de Partículas 10.000 veces más potente que el LHC, donde las partículas pueden adquirir esas tantas veces más energías de las alcanzadas actualmente. Las colisiones que tendrían lugar nos dirían algo acerca de los detalles estructurales de esas partículas que no conocemos, que serían mucho más pequeños que los que ahora podemos contemplar. En este punto se me ocurre la pregunta: ¿Seguiría siendo correcto el Modelo estándar? 0, por el contrario, a medida que nos alejemos en las profundidades de lo muy pequeño, también sus normas podrían variar al mismo tiempo que varían las dimensiones de los productos hallados. Recordad que, el mundo no funciopna de la misma manera ante lo grande que ante lo infinitesimal.

bosón W⁺, que hasta los científicos tardaban meses en conseguir con  el LHC obtiene en menos de un mes.

¿Podeis imaginar conseguir colisiones a 70.000 TeV? ¿Que podrías ver? Y, entonces, seguramente, las protestas de algunas de que “ese monstruo” podría abrir un agujero de gunsano en el espacio tiempo…¡tendría algún fundamento! No sabemos lo que pasar si andamos con fuerzas que no podemos dominar.

Hoy, el Modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero tenemos algunas razones sospechar que tales predicciones resultan estar muy alejadas de la realidad, o, incluso, ser completamente falsas.

Encendamos nuestro supermicroscopio imaginario y enfoquemosló directamente en el centro de un protón o de cualquier otra partícula. Veremos hordas de partículas fundamentales desnudas pululando. Vistas a través del supermicroscopio, el modelo estándar que contiene veinte constantes naturales, describen las fuerzas que rigen la forma en que se mueven. Sin embargo, esas fuerzas no sólo son bastante fuertes sino que también se cancelan entre ellas de una forma muy especial; están ajustadas para conspirar de tal manera que las partículas se comportan como partículas ordinarias cuando se vuelven a colocar el microscopio en la escala de ampliación ordinaria. Si en nuestras ecuaciones matemáticas cualquiera de estas constantes fueran reemplazadas por un ligeramente diferente, la mayoría de las partículas obtendrían inmediatamente masas comparables a las gigantescas energías que son relevantes en el dominio de las muy altas energías. El hecho de que todas las partículas tengan masa que corresponden a energías mucho menores repentinamente llega a ser bastante poco natural.

¿Implica el ajuste fino un diseño con propósito? Hay tantos parámetros que deben tener un ajuste fino y el grado de ajuste fino es tan alto, que no parece posible ninguna otra conclusión.

Bueno, quizá en la imagen y el comentario que lleva abajo, me he podido pasar un poco. Lo que decía: “El hecho de que todas las partículas tengan masa que corresponden a energías mucho menores repentinamente llega a ser bastante poco natural”, es lo que se llama el “problema del ajuste fino”. Vistas a través del microscopio, las constantes de la Naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. un punto de vista matemático, no hay nada que objetar, pero la credibilidad del Modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas o, lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas.

¿Y por qué debería ser el modelo válido hasta ahí? Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables, e ellas podrían modificar completamente el mundo que Gulliver planeaba visitar. Si deseamos evitar la necesidad de un delicado ajuste fino de las constantes de la Naturaleza, creamos un problema:

La masa del bosón de Higgs y del quark top (cima) apuntan a que el vacío del modelo estándar es metaestable, aunque no estamos del todo seguros porque está en el borde estable y metaestable. Además, los errores son muy grandes, tanto los experimentales, sobre todo en la masa del quark top, como los teóricos, hay que extrapolar los cálculos hasta la escala de Planck y las correcciones de mayor orden podrían ser importantes. Quizás sea por puro azar, o quizás haya algo profundo oculto, pero las masas del Higgs y del quark top parecen ajustadas en un punto crítico doble en relación a la estabilidad del vacío.

¿Cómo podemos modificar el modelo estándar de tal manera que el ajuste-fino no sea necesario? Está claro que las moficiaciones son necesarias , lo que implica que muy probablemente hay un límite más allá del cual ewl modelo deja de ser válido. El Modelo estándar no será más que una aproximación matemática que hemos sido capaces de crear, tal que todos los fenómenos observados hasta el presente están de acuerdo con él, pero vez que ponemos en marcha un aparato más poderoso, debemos esperar que sean necesarias nuevas modificaciones para ir ajustando el modelo, a la realidad que descubrimos.

¿Cómo hemos podido pensar de otra manera? ¿Cómo hemos tenido la “arrogancia” de pensar que podemos tener la teoría “definitiva”? Mirando las cosas de esta manera, nuestro problema puede muy bien ser el opuesto al que plantea la pregunta de dónde acaba el modelo estándar: ¿cómo puede ser que el modelo estándar funcione tan extraordinariamente bien? y ¿por qué aún no hemos sido capaces de percibir nada parecido a otra generación de partículas y fuerzas que no encajen en el modelo estándar?

Asistentes escuchan la presentación de los resultados del experimento ATLAS, el seminario del Centro Europeo de Física de Partículas (CERN) para presentar los resultados de los dos experimentos paralelos que buscan la prueba de la existencia de la “partícula de Higgs”, base del modelo estándar de física, hoy miércoles 4 de julio en Meyrin, Suiza.

La pregunta “¿Qué hay más allá del Modelo estándar”? ha facinando a los físicos durante años. Y, desde luego, todos sueñan con llegar a saber, qué es lo que realmente es lo que conforma el “mundo” de la materia, qué partículas, cuerdas o briznas vibrantes. En realidad, lo cierto es que, la Física que conocemos no tiene que ser, necesariamente, la verdadera física que conforma el mundo y, sí, la física que conforma “nuestro mundo”, es decir, el mundo al que hemos podido tener acceso hasta el momento y que, no necesariamente tiene que tratarse del mundo real.

O, decía aquél: ¡Que mundo más hermoso, parece de verdad!

No todo lo que vemos es, necesariamente, un reflejo de la realidad de la Naturaleza que, puede tener escondidos más allá de nuestras percepciones, otros escenarios y otros objetos, a los que, por , no hemos podido acceder, toda vez que, físicamente tenemos carencias, intelectualmente también, y, nuestros conocimientos avanzar despacio para conseguir, nuevas máquinas y tecnologías nuevas que nos posibiliten “ver” lo que ahora nos está “prohibido” y, para ello, como ocurre siempre, necesitamos energías de las que no disponemos.

Hay dos direcciones a lo largo de las cuales se podría extender el Modelo estándar, tal lo conocemos actualmente, que básicamente se caraterizan así:

– Nuevas partículas raras y nuevas fuerzas extremadamente débiles, y

– nuevas partículas pesadas y nuevas estructuras a muy altas energías.

Podrían existir partículas muy difíciles de producir y de detectar y que, por esa razón, hayan pasado desapaercibidas ahora.  La primera partícula adicional en la que podríamos  pensares un neutrino rotando a derecha. Recordaremos que si se toma el eje de rotación aparalelo a la dirección del movimiento los neutrinos sólo rotan a izquierdas , esa sería otra historia.

En un artículo editado en Ciencia Kanija, pude leer: “Los interferómetros atómicos tienen ahora la sensibilidad para observar nuevas fuerzas más allá del modelo estándar de la física de partículas. “Las nuevas fuerzas a corta distancia son una predicción frecuente de las teorías más allá del Modelo Estándar y la búsqueda de estas nuevas fuerzas es un canal prometedor para una nueva física”, dice Jay Wackerdel Laboratorio del Acelerador Nacional SLAC en California. La pregunta es cómo encontrarlas”

Los neutrinos siempre me han fascinado. Siempre se han manifestado como si tuvieran masa estrictamente nula. Parece como si se movieran exactamente con la velocidad de la luz. Pero hay un límite la precisión de nuestras medidas. Si los neutrinos fueran muy ligeros, por ejemplo, una cienmillonésima de la masa del electrón, seríamos incapaces de detectar en el laboratorio la diferencia éstos y los neutrinos de masa estrictamente nula. , para ello, el neutrino tendría que tener una componente de derechas.

En punto, los astrónomos se unen a la discusión. No es la primera vez, ni será la última, que la astronomía nos proporciona información esencial en relación a las partículas elementales. Por ejemplo, debido a las interacciones de corriente neutra (las interacciones débiles originadas por un intercambio Zº), los neutrinos son un facto crucial en la explosión  supernova de una estrella. sabemos que debido a las interacciones por corriente neutra, pueden colisionar con las capas exteriores de la estrella y volarlas con una fuerza tremenda.

En realidad, los neutrinos nos tienen mucho que decir, todavía y, no lo sabemos todo acerca de ellos, sino que, al contrario, son muchos los y fenómenos que están y subyacen en ellos de los que no tenemos ni la menor idea que existan o se puedan producir. Nuestra ignorancia es grande, y, sin embargo, no nos arredra hablar y hablar de cuestiones que, la mayoría de las veces…ni comprendemos.

Aquí lo dejar´ñe por hoy, el tema es largo y de una fascinación que te puede llevar a lugares en los que no habías pensado al comenzar a escribir, lugares maravillosos donde reinan objetos exóticos y de fascinante porte que, por su pequeñez, pueden vivir en “mundos” muy diferentes al nuestro en los que, ocurren cosas que, nos llevan el asombro y también, a ese mundo mágico de lo fascinante y maravilloso.

emilio silvera

 « ¡Qué bonito es saber!

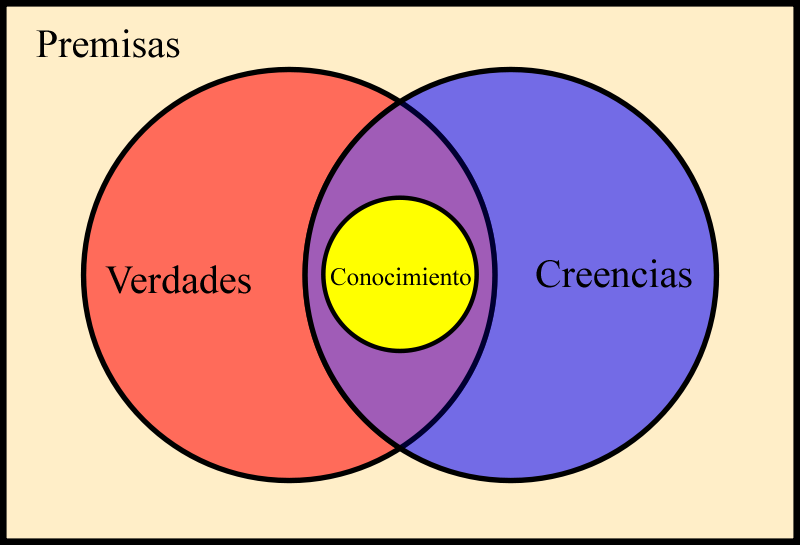
Nuestra realidad es que uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”     Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.

Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, ello, encontramos las maneras de aproximarnos a esa realidad “presentida”.

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado y sobre ese objetivo en particular.

Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas  y conceptos conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un concreto.

                                   En aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado.

Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:

1 – 1/3 + 1/5 – 1/7 ….

Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente,  se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que  independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y  entre otros temas. Si hablamos de  “Pi” mos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN, el efecto mariposa y la Torah, entre otras muchísimas cosas que  se escriben con Pi. Es un misterioso que lo podemos ver por todas partes reopresentado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.

No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada , que deducir el mundo. Yo no dejaría de lado, en todo esto la teoría del Caos  que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus iniciales. El ejemplo más común es conocido como “el efecto mariposa “. La teoría supone que el batir de alas de una mariposa en la China un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.

El escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.

Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han buscando un patrón en el cordón interminable de números.

Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.

¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la /patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.

3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th

Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra , existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejmplo:

Roger Penrose dedicó bastante más tinta en defender  los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.

Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos  lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

                     ¿Es la verdad inalcanzable?

Sin embargo, Roger Penrose, piensa que no, y demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.

Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos , somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos  y dispares pensamientos:

• Los Computadores nunca podrán reemplazar la estupidez humana.
• El hombre nace ignorante,  la educación lo idiotiza.
• Una persona inteligente resuelve problemas, el genio los evita.
• Las consideran que guardar un secreto, es no revelar la fuente.
• Todas las mujeres tienen algo bonito… así sea una prima lejana.
• La felicidad es una lata de atún, con el abrelatas un poco distante.
• El único animal que no resiste aplausos es el mosquito.
• El amor está en el cerebro, no en el corazón.
• Definición de nostalgia “es la alegría de estar triste”.
• “Mi segundo órgano favorito es el cerebro”.

En qué se parecen los hombres a una computadora: En que cuando más lo necesitas, se les cae el sistema.

Vale, ¿y qué consecuencias tiene eso? la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos.

De misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!

Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?

     Todo eso está bien pero, ¿Quien es PI?

Desde hace aproximadamente unos 5000 años, el hombre ha utilizado  objetos que ruedan para ayudarse en sus tareas, por eso es muy probable que haya descubierto ese “3 y pico” hace muchos años, pues es imprescindible para calcular y resolver problemas que involucraran estos cuerpos. la historia, que los antiguos egipcios en el 1600 a. de C. ya sabían que existía una relación entre la longitud de la circunferencia y su diámetro; y entre el área del círculo y el diámetro al cuadrado (seguramente de intuitiva). En el Papiro de Rhind puede leerse lo siguiente:

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. cuadrado tiene el mismo área que el circulo”.

Si llamamos A al área del círculo, ésta será igual a 8/9 del diámetro al cuadrado

     A=(8/9 d)^2

  d=2r entonces   A= 2r^2 x 64/81  = 4r2 x 64/81  = r2 x 256/81

Así vemos como  π adoptaba el valor 256/81, aproximadamente 3,16.  En Mesopotamia, más o menos por la misma época, los babilonios utilizaban el valor 3,125 (3+1/8) según  la Tablilla de Susa.

Mientras que los geómetras de la Grecia clásica sabían que la razón entre la longitud de una circunferencia cualquiera y su diámetro es siempre una constante (el al que ahora llamamos pi). También conocían y habían conseguido demostrar que tanto la razón entre el área de un círculo y su diámetro al cuadrado, como la del volumen de una esfera y el cubo de su diámetro eran constantes (desconocidas en aquel momento, libro XII de “Los Elementos” de Euclides).

Fue Arquímedes en el siglo III a. de C. quien determinó que estas constantes estaban estrechamente relacionadas con π. Además, utilizó el método de exhaución, inscribiendo y circunscribiendo en una circunferencia, polígonos de hasta 96 lados y consiguiendo una magnífica aproximación la época.

Lo cierto es que, tiempos inmemoriales, vamos tras la huella del saber, tratando de adentrarnos en el conocimiento de las cosas que nos rodean, del mundo en el que vivímos, de la Galaxias que nos acoge y en fin, del Universo y la Naturaleza que guarda todos los secretos que deseamos desvelar y, como nosotros somos parte de esa Naturaleza, es posible, quer todas las respuestas que buscamos esté, desde el principio, gravada en nosotros y, sólo con el tiempo, podrán aflorar y llegar a nuestras mentes que tratamos de comprender a veces, con frustración y sufrimiento ante la impotencia de no saber…lo que pueda haber en el interios de tan complejo “universo”.

emilio silvera