Eninstein recibió una carta de un matemático deconocido llamado Kaluza que, elevando la teoría a la quinta dimensión, conseguía unificar la Relatividad con el electromagnetismo de Maxwll. Cuando leyó la carta y comprendió la interessante idea de Kaluza se entusiasmó con ella,  pero pronto comprendió que con esa teoría no se podía predecir nada y la abandonó. La característica esencial de este diagrama de abajo es que la materia, junto con las ecuaciones de Yang-Mills y de Einstein, está incluida en el mismo campo de supergravedad de 11 dimensiones. Veámosloas.

La materia con todas las fuerzas fundamentales de la naturaleza. Los bosones intermediarios o partículas portadoras de las fuerzas como el fotón el electromagnetismo, los gluones para la fuerza nuclear fuerte, las partículas W y Z para la nuclear débil y, en la partícula portadora de la gravedad, el gravitón, ponemos el signo de interrogación, ya que se sabe que esta ahí en algún sitio pero hasta la no ha sido detectado.

Los expertos en supergravedad redescubrieron idea de Kaluza y Klein.Una vez que hemos empezado a considerar muchas dimensiones extra, entramos en una especie de Valhalla de las matemáticas donde podemos enrollar las cosas de muchas maneras diferentes. Las componentes de los campos de fuerza gravitatorias en las direcciones enrolladas actúan como diferentes campos gauge. Obtenemos así, prácticamente por nada, no sólo electromagnetismo sino también otras fuerzas gauge. El mágico de dimensiones es 11, tres de las cuales forman el espacio ordinario, una el tiempo y las siete restantes están enrolladas. Haciendo ciertos trucos con los números, este sistema resulta tener una simetría mayor que nuestro viejo sistema espacio-temporal de cuatro dimensiones. Los campos y las partículas observadas ahora pueden ser fácilmente acomodados, ya que una simetría mayor significa que los indeseados infinitos se cancelan unos a otros con mayor perfección que antes.

Ciertamente esta idea, esta idea parece ser la contraria a la noción de que el espacio y el tiempo sean nada más que puntos aislados, ya que entonces la noción de “dimensión” deja de tener sentido. Pero los matemáticos no se sienten amenazados por tales contracciones aparentes. De acuerdo con ellos,  hay todo de relaciones entre los espacios enrollados y la matemática de los números enteros, “sueltos” (uno podría indicar los puntos aislados del espaciotiempo con enteros). ¿Podría ser que exitieran diferentes formas de describir nuestro espacio y el tiempo que todas fueran matemáticamente equivalentes? Simplemente no lo sabemos.

Lo que sospecho es que la Supergravedad de dimensión once que sólo sea, en el mejor de los casos, la punta de un amravilloso Iceberg, p que sea simplemente errónea.

                                          Se intenta y se utilizan energías inmensas pero, no siempre podemos ver todo lo que hay

No deberíamos olvidar en este  que estamos tratando de suposiciones y que los argumentos teóricos que la sustentan son aún, extremadamente débiles. ¿Por qué supersimetría? ¿Por qué Once Dimensiones? ¿Por qué en este mundo todo debería ser maravillosamente simétrico? Y, sobre todo, ¿por qué un continuo, si ya sabemos que el espacio y el tiempo han perdido su significado habitual a distancias ultracortas? Además está la dificultad persistente en clase de teorías de que las interacciones entre partículas son siempre tratadas como perturbaciones que afectan a sus trayectorias las cuales, de otra manera, serían perfectamente rectilineas.

Pero entonces habrá nuevas (y diferentes) perturbaciones sobre esas trayectorias perturbadas, y perturbaciones sobre ellas, y así sucesivamente. esta serie de perturbaciones no acaba nunca y este es un problema que se impone en cualquier proceso de formulación exacta.

Es cierto que este problema también afecta al viejo “modelo estándar”, pero al menos allí se podría argüir que, donde realmente importaba, las fuerzas podrían mantenerse pequeñas  y que la serie de perturbaciones convergía rápidamente. Esto no se mantener así en nuestra teoría de la (super)  Gravedad, ya que a distancias pequeñas las interacciones se hacen fuertes.

Los Quarks permacen confinados dentro del núcleo formando protones y neutrones y, tratan de separase, la fuerza nuclear fuerte aumenta, en cambio, cuando los Quarks están juntos, se mueven con facilidad y la fuerza disminuye: Libertad asintótica de los Quarkas.

Es cierto que fue un alivio aquellas primeras dificultades serias en esta teoría, u resultó que no era posible tener infinitos que se cancelasen en diagramas con más de siete lazos cerrados. La teoría, o mejor dicho, la especulación de que esto fuese una “teoría de todo” se abandonó (como otras veces ocurrió) porque algo mñás interesante apareció en el horizonte de la Física. ¡Las Supercuerdas!

Aunque hemos hablado mucho de ellas, creo que debemos profundizar algo más en prometedora teoría y, aunque de momento es sólo una especulación avanzada…¿quién sabe? lo que nos podría traer. Hablaremos de ella en próximos trabajos.

emilio silvera

 « Nuestras Mentes…¡que no comprendemos!

Debido al principio de exclusión de Pauli, es imposible que dos fermiones ocupen el mismo cuántico (al contrario de lo que ocurre con los bosones). La condensación Bose-Einstein es de importancia fundamental explicar el fenómeno de la superfluidez. A temperaturas muy bajas (del orden de 2×10^-7º K) se formar un condensado de Bose-Einstein, en el que varios miles de átomos forman una única entidad (un superátomo). efecto ha sido observado con átomos de rubidio y litio. Como ha habréis podido suponer, la condensación Bose-Einstein es llamada así en honor al físico Satyendra Nath Bose (1.894 – 1.974) y a Albert Einstein. Así que, el principio de exclusión de Pauli tiene aplicación no sólo a los electrones, sino también a los fermiones; pero no a los bosones.

Las reglas de la mecánica cuántica tienen que ser aplicadas si queremos describir estadísticamente un sistema de partículas que obedece a reglas de ésta teoría en vez de las de la mecánica clásica.  En estadística cuantica, los estados de energía se considera que están cuantizados.  La estadística de Bose-Einstein se aplica si cualquier de partículas puede ocupar un estado cuántico dado. Dichas partículas (como dije antes) son los bosones que, tienden a juntarse.

         Los bosones tienen un angular n h / 2p, donde n es cero o un entero y h es la constante de Planck.  bosones idénticos, la función de ondas es siempre simétrica.  Si solo una partícula puede ocupar un cuántico, tenemos que aplicar la estadística Fermi-Dirac y las partículas (como también antes dije) son los fermiones que tienen momento angular (n+½) h/2p y cualquier función de ondas de fermiones idénticos es siempre antisimétrica.

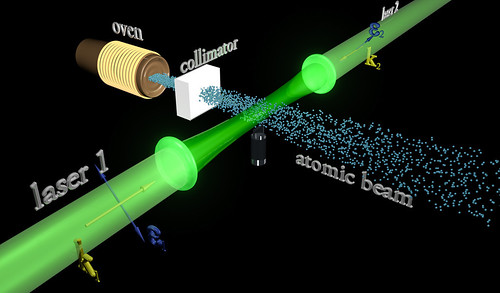
La mejor teoría explicar el mundo subatómico nació en 1928 cuando el teórico Paul Dirac combinó la mecánica cuántica con la relatividad especial para explicar el comportamiento del electrón. El resultado fue la mecánica cuántica relativista, que se transformó en un ingrediente primario en la teoría cuántica de campos. Con unas pocas suposiciones y ajustes ad-hoc, la teoría cuántica de campos ha probado ser suficientemente poderosa para formar la base del modelo estándar de las partículas y las fuerzas.

La relación el espín y la estadística de las partículas está demostrada por el teorema espín-estadística. En un espacio de dos dimensiones es posible que existan partículas (o cuasipartículas) con estadística intermedia entre bosones y fermiones.  Estas partículas se conocen con el de aiones; para aniones idénticos la función de ondas no es simétrica (un cambio de fase de+1) o antisimétrica (un cambio de fase de -1), sino que interpola continuamente entre +1 y -1.  Los aniones pueden ser importantes en el análisis del efecto Hall cuántico fraccional y han sido sugeridos como un mecanismo para la superconductividad de alta temperatura.

Resulta  fácil comprender cómo  un campo magnético la partícula cargada que gira, pero ya no resulta tan fácil saber por qué ha de hacer lo mismo un neutrón descargado. Lo cierto es que cuando un rayo de neutrones incide sobre un hierro magnetizado, no se comporta de la misma forma que lo haría si el hierro no estuviese magnetizado. El magnetismo del neutrón sigue siendo un misterio; los físicos sospechan que contiene cargas positivas y negativas equivalente a cero, aunque por alguna razón desconocida, logran crear un campo magnético cuando gira la partícula.

Particularmente creo que, si el neutrón masa, si la masa es energía (E = mc²), y si la energía es electricidad y magnetismo (según Maxwell), el magnetismo del neutrón no es tan extraño, sino que es un aspecto de lo que en realidad es materia. La materia es la luz, la energía, el magnetismo, en definitiva, la fuerza que reina en el universo y que está presente de una u otra forma en todas partes (aunque no podamos verla).

Sea fuere, la rotación del neutrón nos da la respuesta a esas preguntas:

           La primera demostración efectiva de antimateria se tuvo en Brookhaven en 1.965

¿Qué es el antineutrón? Pues, simplemente, un neutrón cuyo movimiento rotatorio se ha invertido; su polo sur magnético, por decirlo así, está arriba y no abajo. En realidad, el protón y el antiprotón, el electrón y el positrón, muestran exactamente el mismo fenómeno de los polos invertidos. Es indudable que las antipartículas pueden combinarse para formar la antimateria, de la misma que las partículas corrientes forman la materia ordinaria.

La primera demostración efectiva de antimateria se tuvo en Brookhaven en 1.965, donde fue bombardeado un blanco de berilio con 7 protones BeV y se produjeron combinaciones de antiprotones y antineutrones, o sea, un antideuterón. entonces se ha producido el antihelio 3, y no cabe duda de que se podría crear otros antinúcleos más complicados aún si se abordara el problema con más interés.

Pero, ¿existe en realidad la antimateria? ¿Hay masas de antimateria en el universo? Si las hubiera, no revelarían su presencia a cierta distancia. Sus efectos gravitatorios y la luz que produjeran serían idénticos a los de la materia corriente. Sin embargo, cuando se encontrasen las masas de las distintas materias, deberían ser claramente perceptibles las reacciones masivas del aniquilamiento mutuo resultante del encuentro. Así pues, los astrónomos observan especulativamente las galaxias, tratar de encontrar alguna actividad inusual que delate interacciones materia-antimateria.

…, ¿Hay masas de antimateria en el Universo? ¿Galaxias de antimateria?

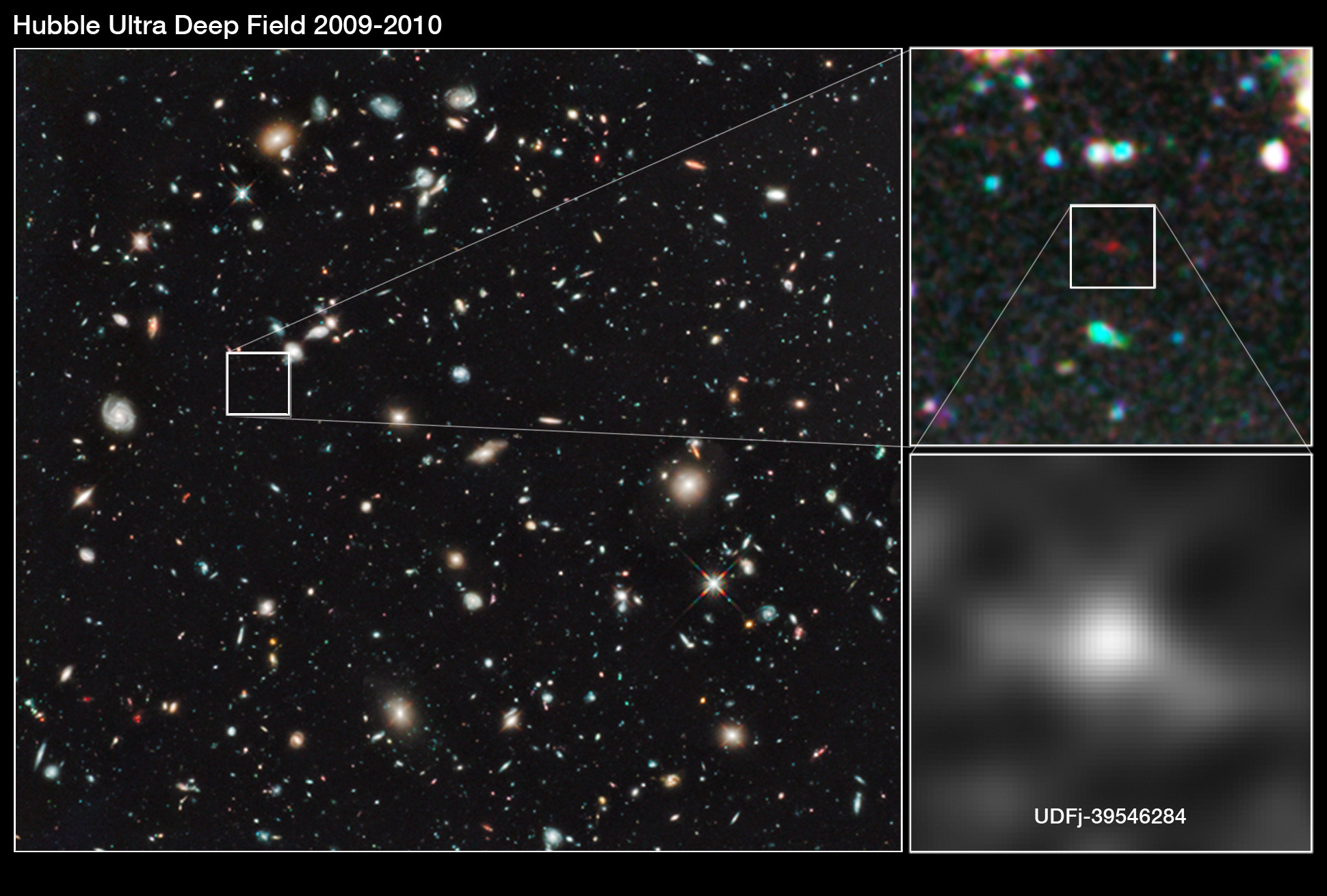
Bueno, sabemos que no son las galaxias las que se alejan, sino que es el espacio el que se expande. Lo que no sabemos es encontrar antimateria en el espacio interestelar y, si la hay y está presente… ¡Aún no la hemos podido localizar! Algunos dicen que hay galaxias de antimateria y, yo digo que tengo un pariente en la galaxia Astrinia del cúmulo Ultramón a diez mil millones de años-luz de nuestra región.

         No parece que dichas observaciones, al menos hasta el , hayan sido un éxito.

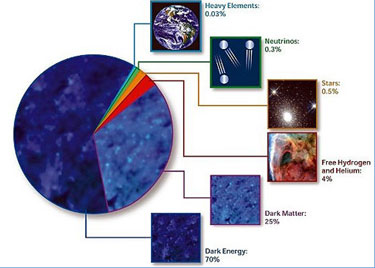
Según estimaciones recientes, resumidas en gráfico de la NASA, alrededor del 70% del contenido energético del Universo consiste en energía oscura, cuya presencia se infiere en su efecto sobre la expansión del Universo pero sobre cuya naturaleza última no se sabe casi nada.

         ¿Es posible que el Universo este formado casi enteramente por materia, con muy poca o ninguna antimateria? Y si es así, ¿por qué? dado que la materia y la antimateria son equivalentes en todos los aspectos, excepto en su oposición electromagnética, cualquier fuerza que crease una originaria la otra, y el Universo debería estar compuesta de iguales cantidades de la una y de la otra.

         Este es el dilema.  La teoría nos dice que debería haber allí antimateria, pero las observaciones lo niegan, no lo respaldan. ¿Es la observación la que falla? ¿Y qué ocurre con los núcleos de las galaxias activas, e incluso más aún, con los causares? ¿Deberían ser estos fenómenos energéticos el resultado de una aniquilación materia-antimateria? ¡No creo! Ni siquiera ese aniquilamiento parece ser suficiente, y los astrónomos prefieren aceptar la noción de colapso gravitatorio y fenómenos de agujeros negros como el único mecanismo conocido para producir la energía requerida.

      Estábamos hablando de mecánica cuántica y me pasé, sin que me diera , al ámbirto de la antimateria y el espacio del macro universo de las galaxias. Sin embargo, y aunque parezcan temas dispares, lo cierto es que, a medida que profundizamos en estas cuestiones, todas nos llevan, de una u otra manera,  a relacionar el “mundo de lo muy pequeño” con el “mundo” de lo muy grande que, al fín y al cabo, está hecho de lo que existe en el primero, es decir, partículas infinitesimales de materia y… ¡de antimateria! para que todo quede compensado.

emilio silvera

 « Todo es Universo… ¡También nosotros!

El propio Rutherford empezó a vislumbrar la respuesta a la pregunta que arriba hacemos. 1.906 y 1.908 (hace más de un siglo) realizó constantes experimentos disparando partículas alfa contra una lámina sutil de metal (como oro o platino), para analizar sus átomos. La mayor de los proyectiles atravesaron la barrera sin desviarse (como balas a través de las hojas de un árbol), pero no todos.

 

 

 

 

 

 

En la placa fotográfica que le sirvió de blanco tras el metal, Rutherford descubrió varios impactos dispersos e insospechados alrededor del punto central. Comprobó que algunas partículas habían rebotado. Era como si en vez de atravesar las hojas, algunos proyectiles hubiesen chocado contra algo más sólido. Rutherford supuso que aquella “balas” habían chocado contra una especie de núcleo denso, que ocupaba sólo una parte mínima del volumen atómico y ese núcleo de intensa densidad desviaban los proyectiles que acertaban a chocar contra él. Ello ocurría en muy raras ocasiones, lo cual demostraba que los núcleos atómicos debían ser realmente ínfimos, porque un proyectil había de encontrar por fuerza muchos millones de átomos al atravesar la lámina metálica.

 

 

 

Era lógico suponer, pues, que los protones constituían ese núcleo duro. Rutherford representó los protones atómicos elementos apiñados alrededor de un minúsculo “núcleo atómico” que servía de centro (después de todo eso, hemos podido saber que el diámetro de ese núcleo equivale a algo más de una cienmilésima del volumen total del átomo).

En 1.908 se concedió a Rutherford el premio Nobel de Química por su extraordinaria labor de investigación sobre la naturaleza de la materia. Él fue el responsable de importantes descubrimientos que permitieron conocer la estructura de los átomos en esa primera avanzadilla.

 

 

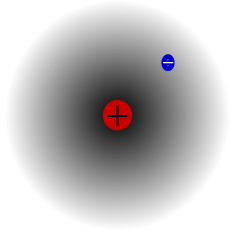
Átomo de hidrógeno, núcleo y electrón.

entonces se pueden describir con términos más concretos los átomos específicos y sus diversos comportamientos. Por ejemplo, el átomo de hidrógeno posee un solo electrón. Si se elimina, el protón restante se asocia inmediatamente a alguna molécula vecina; y cuando el núcleo desnudo de hidrógeno no encuentra por medio un electrón que participe, actúa un protón (es decir, una partícula subatómica), lo cual le permite penetrar en la materia y reaccionar con otros núcleos si conserva la suficiente energía.

 

El helio, que posee dos electrones, no cede uno con tanta facilidad. Sus dos electrones forman un caparazón hermético, por lo cual el átomo es inerte. No obstante, si se despoja al helio de ambos electrones, se convierte en una partícula alfa, es decir, una partícula subatómica portadora de dos unidades de carga positiva.

Hay un tercer elemento, el litio, cuyo átomo tres electrones. Si se despoja de uno o dos, se transforma en ión, y si pierde los tres, queda reducida a un núcleo desnudo, con una carga positiva de tres unidades.

Las unidades de carga positiva en el núcleo atómico deben ser numéricamente idénticas a los electrones que contiene por norma, pues el átomo suele ser un cuerpo neutro, y esta igualdad de lo positivo con lo negativo es el equilibrio. De hecho, los números atómicos de sus elementos se basan en sus unidades de carga positiva, no en las de carga negativa, porque resulta fácil hacer variar el de electrones atómicos dentro de la formación iónica, en cambio se encuentran grandes dificultades si se desea alterar el número de sus protones.

 

 

Apenas esbozado este esquema de la construcción atómica, surgieron nuevos enigmas. El de unidades con carga positiva en un núcleo no equilibró, en ningún caso, el peso nuclear ni la masa, exceptuando el caso del átomo de hidrógeno. Para citar un ejemplo, se averiguó que el núcleo de helio tenía una carga positiva dos veces mayor que la del núcleo de hidrógeno; pero como ya se sabía, su masa era cuatro veces mayor que la de este último. Y la situación empeoró progresivamente a medida que se descendía por la tabla de elementos, e incluso cuando se alcanzó el uranio, se encontró un núcleo con una masa igual a 238 protones, pero una carga que equivalía sólo a 92.

¿Cómo era posible que un núcleo que contenía cuatro protones (según se suponía el núcleo de helio) tuviera sólo dos unidades de carga positiva? Según la más simple y primera conjetura emitida, la presencia en el núcleo de partículas cargadas negativamente y con peso despreciable neutralizaba dos unidades de carga. es natural, se pensó también en el electrón. Se podría componer el rompecabezas si se suponía que en núcleo de helio estaba integrado por cuatro protones y dos electrones neutralizadores, lo cual deja libre una carga positiva neta de dos, y así sucesivamente, llegar al uranio, cuyo núcleo tendría, pues, 238 protones y 146 electrones, con 92 unidades libres de carga positiva. El hecho de que los núcleos radiactivos emitieran electrones (según se había comprobado ya, por ejemplo, en el caso de las partículas beta), reforzó idea general. Dicha teoría prevaleció durante más de una década, hasta que por caminos indirectos, llegó una respuesta mejor como resultado de otras investigaciones.

 

 

 

Pero entre tanto se habían presentado algunas objeciones rigurosas contra dicha hipótesis. Por lo pronto, si el núcleo estaba constituido esencialmente de protones, mientras que los ligeros electrones no aportaban prácticamente ninguna contribución a la masa, ¿cómo se explicaba que las masas relativas de varios núcleos no estuvieran representadas por enteros? Según los pesos atómicos conocidos, el núcleo del átomo cloro, por ejemplo, tenía una masa 35’5 veces mayor que la del núcleo de hidrógeno. ¿Acaso significaba esto que contenía 35’5 protones? Ningún científico (ni entonces ni ) podía aceptar la existencia de medio protón.

Este singular interrogante encontró una respuesta incluso antes de solventar el problema principal, y ello dio lugar a una interesante historia.

 

 

 

 

Los tres isótopos naturales del carbono: carbono-12 (6 protones y 6 neutrones), carbono-13 (6 protones y 7 neutrones) y carbono-14 (6 protones y 8 neutrones). En los tres casos es carbono, tiene el aspecto de carbono y se comporta químicamente como carbono, por tener seis protones (y parte de nuestro organismo, por ejemplo). Sin embargo, sus propiedades físicas varían. Por ejemplo, mientras que el carbono-12 y el carbono-13 son estables, el carbono-14 es inestable y radioactivo: emite radiación beta, uno de sus neutrones “extras” se transforma así en un protón y el núcleo se convierte en nitrógeno-14 (que tiene 7 protones y 7 neutrones), con el aspecto y las propiedades del nitrógeno (por tener 7 protones). Dado que la mitad de la masa del carbono-14 pasa a ser nitrógeno-14 cada 5.730 años aproximadamente (más o menos lo que llevamos de civilización humana), la presencia de este isótopo natural resulta especialmente útil la datación precisa de objetos históricos.

Isótopos; construcción de bloques uniformes

Allá por 1.816, el físico inglés William Prout había insinuado ya que el átomo de hidrógeno debía entrar en la constitución de todos los átomos. Con el tiempo se fueron desvelando los pesos atómicos, y la teoría de Prout quedó arrinconada, pues se comprobó que muchos elementos tenían pesos fraccionarios ( lo cual se tomó el oxígeno, tipificado al 16). El cloro, según dije antes, tiene un peso atómico aproximado de 35’5, o para ser exactos, 35’457. otros ejemplos son el antimonio, con un peso atómico de 121’75, el galio con 137’34, el boro con 10’811 y el cadmio con 112’40.

 

 

 

El Uranio 235 que es el único que de manera natural es apto para la fisión nuclear, es escaso, sólo el 7 por 1.000 es uranio 235, el resto, es uranio 238 que, no es combustible nuclear y, la madera mojada, no arde. Sin embargo, si se bombardea con neutrones lentos del uranio 235, resulta que se convierte en Plutonio 239 que sí, es combustible nuclear válido. ¡Qué no idearemos para conseguir los objetivos!

 

 

 

 

El Uranio es muy radiactivo y si está enriquecido… ¡Ya sabemos las consecuencias!

principios de siglo se hizo una serie de observaciones desconcertantes, que condujeron al esclarecimiento. El inglés William Crookes (el del tubo Crookes) logró disociar del uranio una sustancia cuya ínfima cantidad resultó ser mucho más radiactiva que el propio uranio. Apoyándose en su experimento, afirmó que el uranio no tenía radiactividad, y que ésta procedía exclusivamente de dicha impureza, que él denominó uranio X. Por otra , Henri Becquerel descubrió que el uranio purificado y ligeramente radiactivo adquiría mayor radiactividad con el tiempo, por causas desconocidas. Si se deja reposar durante algún tiempo, se podía extraer de él repetidas veces uranio activo X. decirlo de otra manera, por su propia radiactividad, el uranio se convertía en el uranio X, más radiactivo aún.

Por entonces, Rutherford, a su vez, separó del torio un torio X muy radiactivo, y comprobó también que el torio seguía produciendo más torio X. Hacia aquellas fechas se sabía ya que el más famoso de los elementos radiactivos, el radio, emitía un gas radiactivo, denominado radón. Por tanto, Rutherford y su ayudante, el químico Frederick Soddy, dedujeron que la emisión de sus partículas los átomos radiactivos se transformaron en otras variedades de átomos radiactivos.

 

 

 

El Radón, uno de los llamados gases nobles, es incoloro, inodoro e insípido, además de – nuestro mal- radioactivo. Suele presentarse según el tipo de suelos de determinadas zonas y con la descomposición de uranio, concentrándose en la superficie y siendo “arrastrado” en y por el aire que respiramos, y es en grandes cantidades es un gas  perjudicial para la salud… y que anticipa terremotos.

 

 

Varios químicos que investigaron tales transformaciones lograron obtener un surtido muy variado de nuevas sustancias, a las que dieron nombres tales como radio A, radio B, mesotorio I, mesotorio II y actinio C. Luego los agruparon todos en tres series, de acuerdo con sus historiales atómicos. Una serie se originó del uranio disociado; otra del torio, y la tercera del actinio (si bien más tarde se encontró un predecesor del actinio, llamado protactinio).

En total se identificaron unos cuarenta miembros de esas series, y uno se distinguió por su peculiar esquema de radiación. Pero los productos finales de las tres series fueron idénticos: en último término, todas las cadenas de sustancias conducían al mismo elemento, el plomo.

bien, esas cuarenta sustancias no podían ser, sin excepción, elementos disociados. Entre el uranio (92) y el plomo (82) había sólo diez lugares en la tabla periódica, y todos ellos, salvo dos, pertenecían a elementos conocidos.

 

 

 

En realidad, los químicos descubrieron que aunque las sustancias diferían sí por su radiactividad, algunas tenían propiedades químicas idénticas. Por ejemplo, ya en 1.907 los químicos americanos Herbert Newby McCoy y W. H. Ross descubrieron que el radiotorio (uno entre los varios productos de la desintegración del torio) mostraba el mismo comportamiento químico que el torio, y el radio D, el mismo que el plomo, tanto que a veces era llamado radioplomo. De todo lo cual se infirió que tales sustancias eran en realidad variedades de mismo elemento: el radiotorio, una de torio; el radioplomo, un miembro de una familia de plomos; y así sucesivamente.

En 1.913, Soddy esclareció idea y le dio más amplitud. Demostró que cuando un átomo emitía una partícula alfa, se transformaba en un elemento que ocupaba dos lugares más abajo en la lista de elementos, y que cuando emitía una partícula beta, ocupaba, después de su transformación, el lugar inmediatamente superior. Con arreglo a tal norma, el radiotorio descendía en la tabla hasta el lugar del torio, y lo mismo ocurría con las sustancias denominadas uranio X y uranio Y, es decir, que los tres serían variedades del elemento 90. Así mismo, el radio D, el radio B, el torio B y el actinio B compartirían el lugar del plomo como variedades del elemento 82.

 

 

 

 

Soddy dio el de isótopos (del griego iso y topos, “el mismo lugar”) a todos los miembros de una familia de sustancias que ocupaban el mismo lugar en la tabla periódica. En 1.921 se le concedió el premio Nobel de Química.

El modelo protón–electrón del núcleo concordó perfectamente con la teoría de Soddy sobre los isótopos. Al retirar una partícula alfa de un núcleo, se reducía en dos unidades la carga positiva de dicho núcleo, exactamente lo que necesitaba para dos lugares en la tabla periódica. Por otra parte, cuando el núcleo expulsaba un electrón (partícula beta), quedaba sin neutralizar un protón adicional, y ello incrementaba en una unidad la carga positiva del núcleo, lo cual era como agregar una unidad al atómico, y por tanto, el elemento pasaba a ocupar la posición inmediatamente superior en la tabla periódica de los elementos. ¡Maravilloso!

 

 

 

 

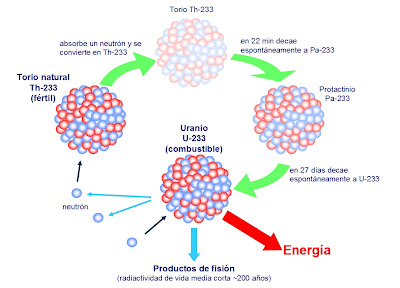
¿Cómo se explica que cuando el torio se descompone en radiotorio después de sufrir no una, sino tres desintegraciones, el producto siga siendo torio? Pues bien, en proceso el átomo de torio pierde una partícula alfa, luego una partícula beta, y más tarde una segunda partícula beta. Si aceptamos la teoría sobre el bloque constitutivo de los protones, ello significa que el átomo ha perdido cuatro electrones (dos de ellos contenidos presuntamente en la partícula alfa) y cuatro protones. (La situación actual difiere bastante de este cuadro, aunque en cierto modo, esto no afecta al resultado).

El núcleo de torio constaba inicialmente (según se suponía) de 232 protones y 142 electrones. Al haber perdido cuatro protones y otros cuatro electrones, quedaba reducido a 228 protones y 138 electrones. No obstante, conservaba todavía el atómico 90, es decir, el mismo de antes.

Así pues, el radiotorio, a semejanza del torio, posee 90 electrones planetarios, que giran alrededor del núcleo. Puesto que las propiedades químicas de un átomo están sujetas al número de sus electrones planetarios, el torio y el radiotorio tienen el mismo comportamiento químico, sea cual fuere su diferencia en peso atómico (232 y 228 respectivamente).

Los isótopos de un elemento se identifican por su peso atómico, o número másico. Así, el torio corriente se denomina torio 232, y el radiotorio, torio 228. Los isótopos radiactivos del plomo se distinguen por estas denominaciones: plomo 210 (radio D), plomo 214 (radio B), plomo 212 (torio B) y plomo 211 (actinio B).

 

 

Se descubrió que la noción de isótopo podía aplicarse indistintamente tanto a los elementos estables como a los radiactivos. Por ejemplo, se comprobó que las tres series radiactivas anteriormente mencionadas terminaban en tres formas distintas de plomo. La serie del uranio acababa en plomo 206, la del torio en plomo 208 y la del actinio en plomo 207. cada uno de estos era un isótopo estable y corriente del plomo, pero los tres plomos diferían por su peso atómico.

Mediante un dispositivo inventado por cierto ayudante de J. J. Thomson, llamado Francis William Aston, se demostró la existencia de los isótopos estables. En 1.919, Thomson, empleando la versión primitiva de aquel artilugio, demostró que el neón estaba constituido por dos variedades de átomos: una cuyo de masa era 20, y otra con 22. El neón 20 era el isótopo común; el neón 22 lo acompañaba en la proporción de un átomo cada diez. Más tarde se descubrió un tercer isótopo, el neón 21, cuyo porcentaje en el neón atmosférico era de un átomo por cada 400.

Entonces fue posible, al fin, razonar el peso atómico fraccionario de los elementos. El peso atómico del neón (20, 183) representaba el peso conjunto de los tres isótopos, de pesos diferentes, que integraban el elemento en su estado natural. Cada átomo individual tenía un número másico entero, pero el promedio de sus masas (el peso atómico) era un número fraccionario.

Aston procedió a mostrar que varios elementos estables comunes eran, en realidad, mezclas de isótopos. Descubrió que el cloro, con un peso atómico fraccionario de 35’453, estaba constituido por el cloro 35 y el cloro 37, en la proporción de cuatro a uno. En 1.922 se le otorgó el premio Nobel de Química.

 

 

 

Sabiendo todo lo anteriormente explicado, hemos llegado a comprender cómo de la Astronomía que estudia las características físicas y químicas de los cuerpos celestes, la astrofísica es la parte más importante de la astronomía en la actualidad debido a que, al avanzar la física moderna: Efecto Doppler-Fizeau, el efecto Zeeman, las teorías cuánticas y las reacciones termonucleares aplicadas al estudio de los cuerpos celestes han permitido que el campo magnético solar, el estudio de las radiaciones estelares y sus procesos de fusión nuclear, y determinar la velocidad radial de las estrellas, etc . radiación electromagnética de los cuerpos celestes permite realizar análisis de los espectros que nos dicen de qué están hechas las estrellas y los demás cuerpos del espacio interestelar y, de esa manera, hemos ido conociendo la materia y sus secretos que, cada vez, van siendo menos.

emilio silvera

 

« El saber ocupa un lugar en nuestras mentes

La partícula emitida por un núcleo radiactivo, por lo general lleva una considerable cantidad de energía. Y, ¿de dónde procede esa energía? Es el resultado de la conversión en energía de una pequeña Los físicos se vieron partícula beta emitida en una desintegración del núcleo no alberga energía suficiente electrones no eran igualmente deficitarios. Emergían con un amplio espectro de energías, y el máximo (corregido por muy pocos electrones) era casi correcto, pero todos los demás no llegaban a alcanzarlo en mayor o partículas alfa emitidas por un nucleido particular poseían iguales energías en cantidades inesperadas. En ese caso, ¿qué era erróneo en la emisión de partículas beta?, ¿qué había sucedido con la energía perdida?

En 1.922, Lise Maitner se hizo por primera vez partícula beta del núcleo se desprendía otra, que se llevaba la energía desaparecida. Esa misteriosa segunda partícula tenía propiedades bastante extrañas; no poseía carga ni masa. Lo único que llevaba mientras se movía a la velocidad de la luz era cierta cantidad de energía. A decir verdad, aquello parecía un cuerpo ficticio creado exclusivamente para equilibrar el contraste de energías.

 

Habitualmente aceptamos que la física es la ciencia que estudia la estructura y propiedades de la materia y la energía, las formas de existencia de las mismas en el espacio y el tiempo, así como las leyes de rigen sus interacciones. En este definición no hay limitaciones precisas Sin embargo, tan pronto como se propuso la posibilidad de su existencia, los físicos creyeron en ella ciegamente. Y neutrón y al saberse que se desintegraba en un protón y liberaba un electrón que, Fermi dio a esta partícula putativa el El neutrón dio a los físicos otra prueba palpable de la existencia del neutrino. Como ya he comentado en otra página de este trabajo, casi todas las partículas describen un movimiento rotatorio. Esta rotación se expresa, más o menos, en múltiplos de una mitad, según la dirección del giro. protón, el neutrón y el electrón tienen rotación de una mitad. Por tanto, si el neutrón con rotación de una mitad origina un protón y un electrón, cada uno con rotación de una mitad, ¿qué sucede con la ley sobre conservación del protón y el electrón totalizan una mitad con sus rotaciones (si ambas rotaciones siguen la misma dirección) o cero (si sus rotaciones son opuestas); pero sus rotaciones no pueden sumar jamás una mitad. Sin embargo, por otra neutrino viene a solventar la cuestión. Supongamos que la rotación del neutrón sea +½, y admitamos protón sea +½ y la del electrón -½, neutrino una rotación de +½ y la balanza quedará desequilibrada.

+½ (n) = +½ (p) – ½ (e) + ½ (neutrino)

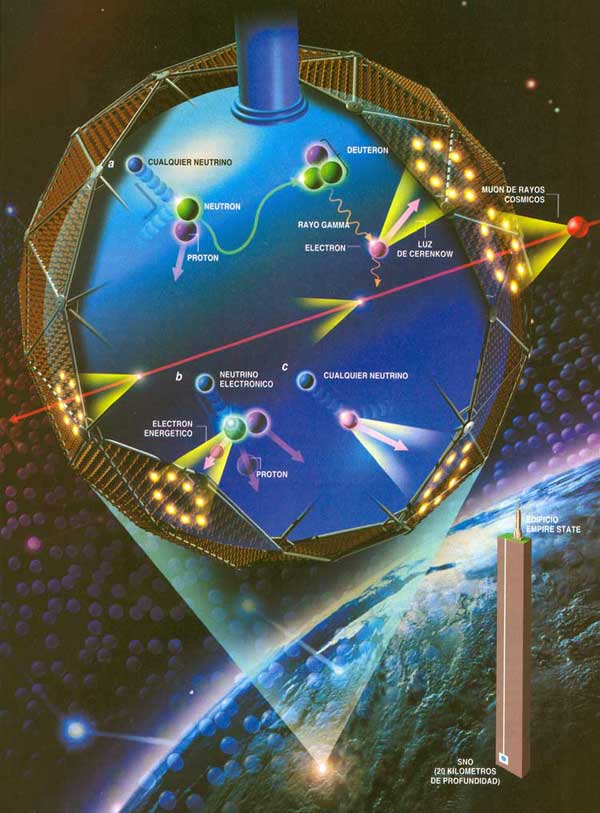
En otras palabras, la existencia de neutrinos y antineutrinos debería salvar no una, sino tres, importantes leyes de conservación: la conservación de la energía, la de conservación del espín y la de conservación de partícula/antipartícula.

neutrón) ha formado dos partículas (el protón y el electrón), y si incluimos el neutrino, tres partículas. Parece más razonable suponer que el neutrón se convierte en dos partículas y una antipartícula. En otras palabras: lo que realmente necesitamos equilibrar no es un neutrino, sino un antineutrino.

El propio neutrino surgiría de la conversión de un protón en un neutrón. Así pues, los productos serían un neutrón (partícula), un positrón (antipartícula) y un neutrino (partícula). Esto  

Impresionante vista de la Vía Láctea Es importante conservar esas leyes puesto que parece estar presentes en toda clase de relaciones nucleares que no impliques electrones o positrones, y sería muy útil si protón–neutrón son las relacionadas con las reacciones nucleares que se desarrollan en el Sol y en los astros. Por consiguiente, las estrellas emiten radiaciones rápidas de neutrinos, y se calcula que tal vez pierdan a causa de esto el 6 u 8% de su energía. Pero eso sería meternos en otra historia y, por mi Desde que puedo recordar, he sido un amante de la física. Me asombran cuestiones

Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales grandes o muy pequeños como las galaxias o los electrones, son materia. La luz, sin embargo, se cree que es inmaterial; dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo creo que la luz es simplemente una Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) Cuando la luz entra en un cristal o en alguna sustancia transparente, de una  

¿Nos suplirán un día? Seguro que en el futuro, serán otros los que hagan experimentos con la luz y busquen su verdadera naturaleza

Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta de las