Ago
4
El placer de Descubrir: Aventurarse por nuevos caminos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber: ¡Ese viaje interminable! ~
Clasificado en El saber: ¡Ese viaje interminable! ~
 Comments (0)
Comments (0)

“En física teórica, las D-branas son una clase especial de P-branas, nombradas en honor del matemático Johann Dirichlet por el físico Joseph Polchinski. Las condiciones de contorno de Dirichlet se han utilizado desde hace mucho en el estudio de líquidos y de la teoría del potencial, donde implican especificar una cierta cantidad a lo largo de toda una frontera. En la dinámica de fluidos, la fijación de una condición de límite de Dirichlet podía significar asignar una velocidad del fluido conocida a todos los puntos en una superficie; al estudiar electrostática, se puede establecer condiciones límite de Dirichlet por la fijación de los valores conocidos del voltaje en localizaciones particulares, como las superficies de los conductores. En cualquier caso, las localizaciones en las cuales se especifican los valores se llaman una D-brana. Estas construcciones adquieren importancia especial en teoría de cuerdas, porque las cuerdas abiertas deben tener sus puntos finales unidas a D-branas.
Las D-branas se clasifican típicamente por su dimensión, que es indicada por un número escrito después de la D. Una D0-brana es un solo punto, una D1-brana es una línea, una D2-brana es un plano, y una D25-brana llena el espacio hiper-dimensional considerado en la teoría de la cuerda bosónica.”
Es ampliamente sabido que el planeta Tierra actúa como un gran imán cuyas líneas de campo geomagnético surgen de un polo (el polo sur magnético) y convergen en el otro polo (polo norte magnético). El eje longitudinal de este imán tiene una desviación de aproximadamente 11^o con respecto al eje de rotación. Por ello, los polos del campo magnético generado no coinciden exactamente con los polos geográficos.
Este campo geomagnético es producido por la combinación de varios campos generados por diversas fuentes, pero en un 90% es generado por la exterior del núcleo de la Tierra (llamado Campo Principal o “Main Field”).
Por otra , la interacción de la ionosfera con el viento solar y las corrientes que fluyen por la corteza terrestre componen la mayor del 10% restante. Sin embargo, durante las tormentas solares (eventos de actividad solar exacerbada) pueden introducirse importantes variaciones en el campo magnético terrestre.
Las grandes tormentas solares inciden sobre nosotros y nuestras obras
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
![[stephan_quinteto_2009_hubble.jpg]](http://3.bp.blogspot.com/_xBXZbW6ivIs/SqpvjP3SBJI/AAAAAAAAEqc/fh3ULAFurbs/s1600/stephan_quinteto_2009_hubble.jpg)
Muchas veces he comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).
La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.

- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.
La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.

Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.

La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10–15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.
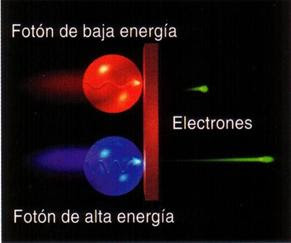
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.

Una de las fuentes productoras de rayos cósmicos es el Sol
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
emilio silvera
Ago
4
¡La perfección! ¿No serán simples rumores?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Belleza y la Ciencia ~
Clasificado en La Belleza y la Ciencia ~
 Comments (1)
Comments (1)


Inmersos en una complejidad que llamamos Universo, nosotros, los humanos, habiendo adquirido la consciencia de Ser hemos llegado a tener un concepto de nosotros que, a veces, sobrepasa los límites de la realidad, toda vez que, siendo entes vivos y pensantes, generadores de ideas y de pensamientos, de sentimientos también, no queremos percatarnos de que estamos supeditados a fuerzas y energías que no podemos dominar, y, es la Naturaleza la que rige en todos nustros actos y nos hace “bailar” al son que “ella” toca. Y, mientras tanto, hacemos cosas, aprendemos y nos equivocamos, tratamos de saber y, de nosotros surgen cosas hermosas.

Espíritu de belleza, que has consagrado
Con tus propios matices todo aquello sobre lo que brillas
Del pensamiento o la Humanos, ¿adonde has ido?
¿Por qué has desaparecido y abandonado nuestra existencia.

oscuro Valle de lágrimas, vacío y desolado.
El Universo está construido según un plan
cuya profunda simetría está presente de algún
modo en la estructura interna de nuestro intelecto.
El primero pretende ser un himno a la Belleza intelectual de Shelley y, en el segundo Paul Valery, nos transmite la idea de que, la belleza, forma de nuestro intelecto humano que, no simplemente valora lo material sino que, de alguna manera, deja un lugar para la excelencia del mundo.

Henry Poincaré
Algunas veces, los físicos teóricos, como los artistias (uno se siente tentado a decir: como otros artistas) se seguían en su trabajo por preocupaciones estéticas tanto como racionales. “Para ciencia, es necesario algo más que la pura lógica”, escribió Poincaré, quien identificaba este elemeto adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza” de los esquemas matemáticos que la Naturaleza nos presenta.
Usted debe hacer sentido esto -le dijo a Einstein, la casi temible simplicidad e integridad de la relación que la Naturaleza repentinamente extiende ante nosotros”. Paul Dirac, el físico teórico y enorme matemático, cuya descripción relativista del electrón está a la altura de las obras maestras de Einstein y Bohr, llegó sostemer que “más importante que nuestras ecuaciones se ajusten a los experimentos es que sean bellas”.

La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la Belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por ese sol central de la simetría.
La simetría es un concepto venerable y en modo alguno inescrutable, que tiene muchas implicaciones en la ciencia y el arte, mucho después de que el físico chino – norteamericano Chen Ning Yang ganase el Premio Nobel por su en el desarrollo de una teoría de campos basada en la simetría, aún afirmaba que “no comprendo todavía todo el alcance del concepto de simetría”.

Debajo de las manifestaciones visibles y audibles de simetría hay profundas invariancias matemáticas. Los esquemas espirales que se encuentran en el interior del nautilu, en la superficie de los girasoles, por ejemplo, pueden ser presentados por aproximación medianter la serie de Fibonacci, una operación aritmética en la que cada miembro es igual a la suma de los dos precedentes (, 1, 2, 3, 5, 8, 13, 21, 34, …). La razón creada dividiendo cada de la serie por el número que le sigue se aproxima al valor 0,618.
No es casual que esta sea la fórmula de la “sección aurea”, una proporción geométrica que aparece en el Partenón, La Mona Lisa y El nacimiento de Venus de Boticelli, y es la base de la octava que se emplea en la músuca occidental el tiempo de Bach. Toda la fecunda diversidad de esta simetría particular, expresada en infinidad de modos, desde conchas marinas y las piñas hasta el Clave buien temperado, deriva, por lo tanto, de una sola unvariancia, la de la serie de Fibonacci. La comprensión de que una sola simetria abstracta podría tener tantas frustíferas y diversas manifestaciones deleitó a los sabios del Renacimiento, quines la citaban como prueba de la eficacia de las matemáticas y de la sutileza de los designios de la Naturaleza sabia. Desde entonces, otras muchas simetías abstractas han sido identificadas en la naturaleza -algunas intactas y otras , “rotas” o estropeadas-, y sus efectos parecen incluso extenderse hasta los cimientos mismos de la materia y la energía.



El Partenón de Atenas. La Grecia clásica , fuente de simetría y canon, presente en todas las imágenes de arriba
La palbra simetría en griego, significa “la misma medida” (sun significa “juntos”, como en sinfonía, una unión de sonidos, metrón, “medición”); así, su etimología nos informa que la simetría para los griegos también significa la “debida proporción” , lo que sugiere que la repetición involucrada debe ser armoniosa y placentera; esto indica que una relación simétrica debe ser juzgada por un criterio estético superior. Pero en la ciencia del siglo XX se puso de relieve el primer aspecto de la vieja definición: se dice que hay simetría una cantidad medible permanece invariante (lo que significa que no cambia) bajo una transformación (que significa una alteración).
Nosotros, casi todos, hemos conocido la simetría en sus manifestaciones geométricas, o, en el Arte. Cuando decimos, por ejemplo, que una esfera tiene una simetrtía de rotación, lo que tratamos de indicar es que poseer unas características -en este caso, su perfil circular- que permanece invariante en las transformaciones producidas al hacerla rotar. Puede hacerso rotar la esfera en cualquier eje y cualquier grado sin que cambie su perfil, lo cual hace que sea más simétirca, por ejemplo, que un cilibro, que tiene una simetría similarsólo cuando rota alrededor de su eje largo; si rota alrededor de su eje corto, el cilindro se reduce a un círculo.

Las simetrías son comunes en las esculturas, empezamdo por el desnudo humano, que es (de modo aproximado) bilateralmente simétrico cuando se le contempla de frente o de atrás, y en arquitectura como en los planos de suelo en forma de cruz

Hay muchas simetrías en la música de Bach, en un pasaje de la Tocata y Fuga en Mi menor (mo he podido encontrar la partitura) traslada arrina y abajo del pentagrama pequeños trios de notas tiendas de campaña. Excepto con la ocasional diferencia de alguna que otra nota, la construcción tiene una simetría de traslación. Si quitamos un trío cualquiera y lo pusiéramos sobre otro, encajaría perfectamente.

Nos encontramos simetrías en el Universo, en el mundo que habitamos, también en nosotros y, nuestras Mentes, no son una excepción y en ellas subyace una simetría más profunda que trasciende a lo material.
emilio silvera
Ago
4
¿Convertir energía en materia? Será por soñar
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Cosas curiosas ~
Clasificado en Cosas curiosas ~
 Comments (0)
Comments (0)

En el pasado mes de mayo, algunos medios publicaron la noticia de que unos científicos habían logrado convertir Luz en Materia y, le ponían la coletilla de que… “El proceso recrea lo que ocurrió en los primeros 100 segundos del universo conocido”. La noticia decía:
“Científicos han logrado hacer materia a partir de luz pura, comprobando una teoría que fue descrita hace 80 años y en cierta forma llevando a cabo un principio universal de transformación. La idea de hacer materia con luz primero fue descrita por Gregory Breit y John Wheeler y en ese entonces creía que era imposible de realizar en el laboratorio, aunque evidentmente la famosa fórmula de Einsten E=mc2 indica que la materia y la energía son convertibles. Y ahora también, de manera empírica, la luz y la materia son intercambiables.
Para poder realizar esta asombrosa comprobación, físicos del Imperial College of London usaron lásers de alta energía y otros aparatos que existen en por lo menos en tres laboratorios en el mundo. Para materializar la luz, primero se disparan electrones a un bloque de oro, lo que produce un haz de fotones de alta energía. Luego se dispara un láser de alta energía a una cápsula llamada holhraum (“cuarto vacío” en alemán). Esto produce una luz tan brillante como la de las estrellas. En la etapa final, se dirige el primer haz de fotones al holhraum donde los flujos de fotones chocan: esto crea partículas subatómicas con masa. Suena como una especie de moderna receta de la piedra filosofal o un arma demiúrgica (aunque los científicos advierten que esto no permitirá materializar objetos de la nada y menos espadas de luz).”

“Sí, sería posible convertir energía en materia, hacerlo en grandes cantidades resulta poco práctico. Veamos por qué. Según la teoría de Einstein, tenemos que E = mc2, donde E representa la energía, medida en ergios, m representa la masa, medida en gramos, y c es la velocidad de la luz en centímetros por segundo. La luz se propaga en el vacío a una velocidad aproximada a los 30.000 millones (3×1010) de centímetros por segundo. La cantidad c2 representa el producto c×c, es decir: 3×1010 × 3×1010, ó 9×1020. Por tanto, c2 es igual a 900.000.000.000.000.000.000. Así pues, una masa de un gramo convertirse, en teoría, en 9×1020 ergios de energía.

Convertir la energía en materia requiere el poceso contrario al de converti la masa en energía, y, luego, se necesitaría una inmensa cantidad de energía para conseguir algo de masa. Fijémonos en que un fotón gamma, por ejemplo, aún siendo muy energético, sólo daría lugar a un electrón y un positrón (siendo la masa de ambos ridícula).
El ergio es una unida muy pequeña de energía que equivale a: “Unidad de o energía utilizado en el sistema c.g.s y actúa definida como trabajo realizado por una fuerza de 1 dina cuando actúa a lo largo de una distancia de 1 cm: 1 ergio = 10-7 julios”. La kilocaloría, de quizá mucho más conocido, es igual a unos 42.000 millones de ergios. Un gramo de materia convertido en energía daría 2’2×1010 (22 millones) de kilocalorías. Una persona sobrevivir cómodamente con 2.500 kilocalorías al día, obtenidas de los alimentos ingeridos. Con la energía que representa un solo gramo de materia tendríamos reservas para unos 24.110 años, que no es poco para la vida de un hombre.
O digámoslo de otro modo: si fuese posible convertir en energía eléctrica la energía representada por un solo gramo de materia, bastaría tener luciendo continuamente una bombilla de 100 vatios durante unos 28.200 años.

Claro que una cosa es convertir la masa en energía y otra muy distinta lo contrario, pero ¿ sería posible convertir energía en materia? Bueno, ya antes hemos dado la respuesta: Sí, pero a costa de un gasto ingente de energía que haría el poceso demasiado costoso y poco rentable. Fijémonos en estos ejemplos:
La energía que representa un gramo de materia equivale a la que se obtendría de quemar unos 32 millones de litros de gasolina. Nada tiene de extraño, por tanto, que las bombas nucleares, donde se convierten en energías cantidades apreciables de materia, desaten tanta destrucción.
La conversión opera en ambos sentidos. La materia se convertir en energía y la energía en materia. Esto último puede hacerse en cualquier momento en el laboratorio, donde continuamente convierten partículas energéticas (como fotones de rayos gamma) en 1 electrón y 1 positrón sin ninguna dificultad. Con ello se invierte el proceso, convirtiéndose la energía en materia.

De momento, no hemos podido conseguir gran cosa para fines pacíficos en lo que a las reacciones nucleares se refiere. Si acaso la energía de fisión de las Centrales nucleares que, en realidad, no es muy aconsejable, y, por otro lado, con fines armamentísticos con las bombas atómicas y de otro que utilizan la fusión.
Pero estamos hablando de una transformación de ínfimas cantidades de masa casi despreciable. ¿Pero podremos utilizar el mismo principio para conseguir cantidades mayores de materia a partir de energía?
Bueno, si un gramo de materia puede convertirse en una cantidad de energía igual a la que produce la combustión de 32 millones de litros de gasolina, entonces hará falta toda esa energía para fabricar un solo gramo de materia, lo que nos lleva al convencimiento de que no sería muy rentable el proceso”.
Fuente: Isaac Asimov
















 Totales: 75.487.510
Totales: 75.487.510 Conectados: 62
Conectados: 62
























