Ago
14
Buscando la Gravedad cuántica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo asombroso ~
Clasificado en El Universo asombroso ~
 Comments (1)
Comments (1)

Todo el ritmo del Universo está en nosotros que somos parte de él, la que piensa. Y, queremos buscar respuestas y desvelar secretos de la Naturaleza que nos somete a continuas pruebas que no podemos superar. Las preguntas son más que las respuestas y, a cada conocimiento nuevo, aparecen mil preguntas que no podemos contestar. Pero… ¡seguimos buscando!

¿Qué ingenio tecnológico haría falta para medir la fuerza de gravedad entre dos partículas?
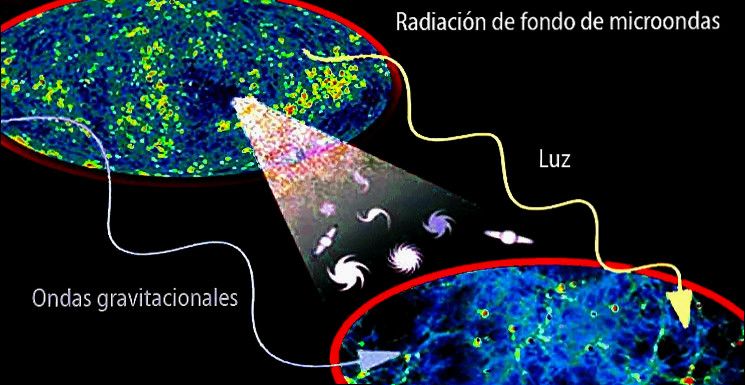
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “Teoría de Yodo o Gran Teoría Unificada”. Es decir, una Teoría en la que estuvieran todas las respuestas… ¡Un sueño! Los Físicos teóricos hablan de la Gravedad cuántica que trata de unificar el Modelo estándar que ya tiene dentro a tres de las cuatro fuerzas fundamentales, con la Gravedad mediante una buena estructura matemática unificada que describa el comportamiento de la Naturaleza sin dejar fuera a ninguna de sus fuerzas como ocurre ahora que, han dejado fuera del Modelo estándar a la Gravedad que se resiste a estar junto a las otras tres fuerzas. Así, continúan persiguiendo ese sueño llamado Teoría de Campo Unificado.
Claro que una teoría cuántica de la gravedad debe generalizar dos teorías de supuestos y formulación radicalmente diferentes:
- La teoría cuántica de campos que es una teoría no determinista (determinismo científico) sobre campos de partículas asentados en el espacio-tiempo plano de la relatividad especial (métrica de Minkowski) que no es afectado en su geometría por el momento lineal de las partículas.
- La teoría de la relatividad general que es una teoría determinista que modela la gravedad como curvatura dentro de un espacio-tiempo que cambia con el movimiento de la materia y densidades energéticas.

La geometría del espacio la determina la materia presente
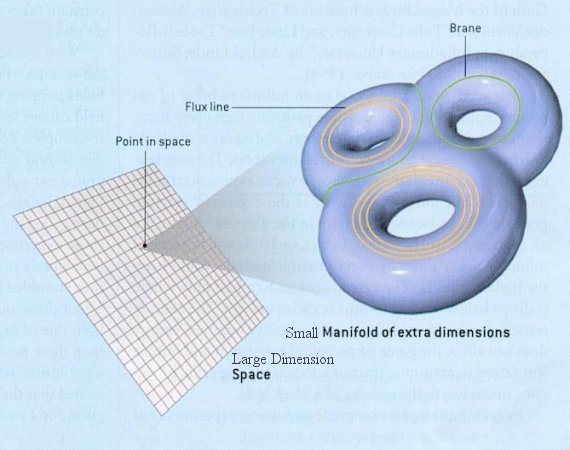
Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
¿Quién puede ir a la longitud de Planck para verlas?

Ni vemos la longitud de Planck ni las dimensiones extra
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?

Nuestro es tridimensional y no podemos ver otro más allá… ¡si existe!
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que con sus 14 TeV no llegaría ni siquiera a vislumbrar esas cuerdas vibrantes de las que tanto se habla.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.

Con sus 20 parámetros aleatorios (parece que uno de ellos ha sido hallado -el bosón de Higgs-), el Modelo estándar de la f´çisica de partículas que incluye sólo tres de las interacicones fundamentales -las fuerzas nucleares débil y fuerte y el electromagnetismo-, ha dado un buen resultado y a permitido a los físicos trabajar ampliamente en el conocimiento del mundo, de la Naturaleza, del Universo. Sin embargo, deja muchas preguntas sin contestar y, lo cierto es que, se necesitan nuevas maneras, nuevas formas, nuevas teorías que nos lleven más allá.
¡Necesitamos algo más avanzado!
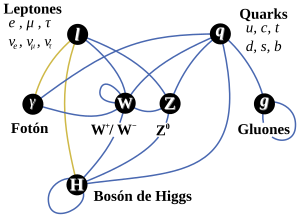
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que conocemos y están incluidas en el Modelo estándar, se nos ha dicho que ha sido encontrada pero, nada se ha dicho de cómo ésta partícula transmite la masa a las demás. Mucho mejor que los del LHC lo explica en su libro nuestro contertulio Ramón Máquez. Faltan algunas explicaciones.
El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
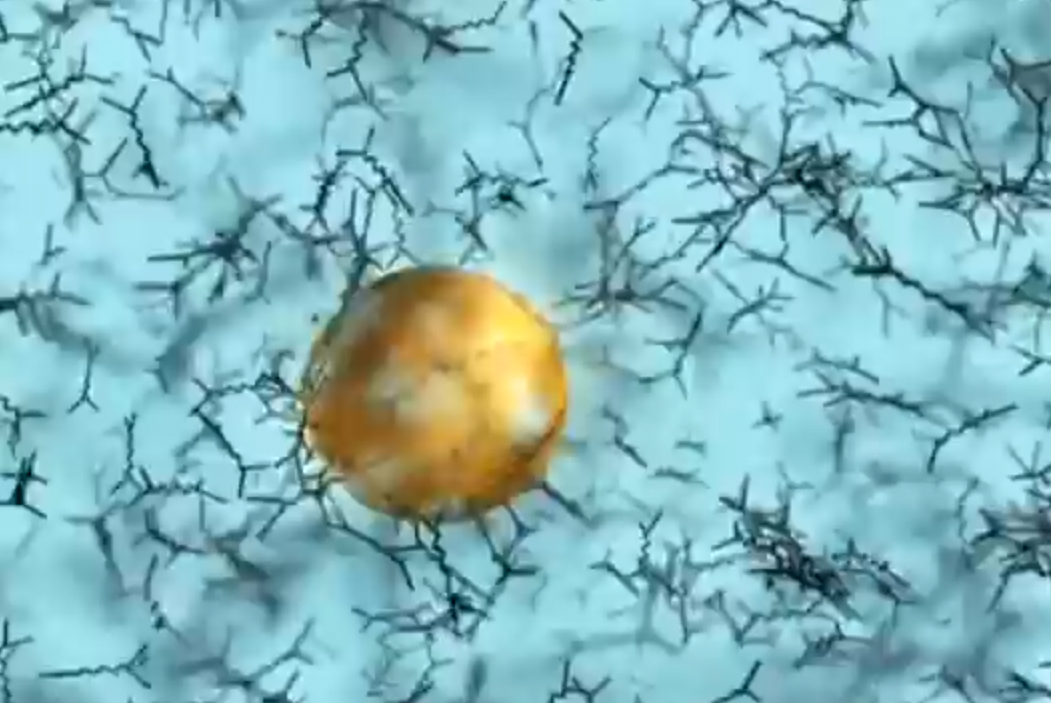
¿Acaso las partículas circulan por el campo de Higgs y se ven frenadas por éste que les adosa la masa?
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.

Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Peor la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más
apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.

La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas –Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

No dejamos de experimentar para saber ccómo es nuestro mundo, la Naturaleza, el Universo que nos acoge
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa –los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.

En esta última dirección ha publicado numerosos libros y artículos, donde aborda la asignatura pendiente de la unificación de la mecánica cuántica y la teoría del campo gravitatorio. El camino que ha seguido Penrose es encontrar una base común a ambas.
Para ello ha introducido dos modelos: los “spin networks” y los “twistors”, el primero discreto, con una métrica intrínseca, no relativista, previo al concepto de espacio, el segundo continuo, con una métrica extrínseca, relativista e inmerso en un espacio-tiempo dado.
Claro que son varias las corrientes que quieren abrirse camino hacia otras físicas nuevas.

“La charla inaugural del congreso anual Strings 2012, 23-28 Julio, MPI, Múnich, Alemania, a cargo de John H. Schwarz (Caltech), uno de los padres de la teoría de cuerdas, no tiene desperdicio. Según él, la teoría de cuerdas y la teoría M no son nada radicales, todo lo contrario, son la prolongación natural de las teorías cuánticas de campos. De hecho, la teoría de cuerdas y la teoría M son la misma cosa que la teoría cuántica de campos (pero escrita en un lenguaje más adecuado, en el sentido de la teoría de la matriz de dispersión (scattering) o matriz S). “

Según lo que podemos entender y hasta donde han podido llegar nuestros conocimientos actuales, ahora sabemos donde están las fronteras: donde las masas o las energías superan 1019 veces la masa del protón, y esto implica que estamos mirando a estructuras con un tamaño de 10-33 centímetros. Esta masa la conocemos con el nombre de masa de Planck y a la distancia correspondiente la llamamos distancia de Planck. La masa de Planck expresada en gramos es de 22 microgramos, que la es la masa de un grano muy pequeño de azúcar (que, por otra parte, es el único de Planck que parece más o menos razonable, ¡los otros números son totalmente extravagantes!). Esto significa que tratamos de localizar una partícula con la precisión de una longitud de Planck, las fluctuaciones cuánticas darán tanta energía que su masa será tan grande como la masa de Planck, y los efectos de la fuerza gravitatoria entre partículas, , sobrepasarán los de cualquier otra fuerza. Es decir, para estas partículas la gravedad es una interacción fuerte.

Sí, a nuestro alrededor podemos contemplar la simetría que en el Universo quedó rota. Que la imaginación que es libre de “volar” hacia espacios desconocidos e infinitos y hacia escenarios imposibles, también puede, no sólo escenificar el hiperespacio, sino que, llevando la fascinación aún más lejos, ¿quién sabe? (como tántas veces hemos comentado), si los teóricos no habrán dado en el blanco y, con su intuición creadora, han podido vislumbrar que toda la materia del universo está formada por cuerdas vibrantes y armónicas que se conjugan de diferentes maneras, produciendo con sus pulsos, nuevas partículas.

También en otras ocasiones hemos recordado que: “En griego, la simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría para los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en la figura que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.”

Buscamos ese Universo fascinante de luz y color en el que la armonía es total y se comprenden todas las cosas
La teoría de supercuerdas tiene tantas sorpresas fantásticas que cualquiera que investigue en el tema reconoce que está llena de magia. Es algo que funciona con tanta belleza… Cuando cosas que no encajan juntas e incluso se repelen, si se acerca la una a la otra alguien es capaz de formular un camino mediante el cual, no sólo no se rechazan, sino que encajan a la perfección dentro de ese sistema, como ocurre ahora con la teoría M que acoge con naturalidad la teoría de la relatividad general y la teoría mecánico-cuántica; ahí, cuando eso se produce, está presente la belleza.
Lo que hace que la teoría de supercuerdas sea tan interesante es que el marco estándar mediante el cual conocemos la mayor parte de la física es la teoría cuántica y resulta que ella hace imposible la gravedad. La relatividad general de Einstein, que es el modelo de la gravedad, no funciona con la teoría cuántica. Sin embargo, las supercuerdas modifican la teoría cuántica estándar de tal manera que la gravedad no sólo se convierte en posible, sino que forma parte natural del sistema; es inevitable para que éste sea completo.
¿Por qué es tan importante encajar la gravedad y la teoría cuántica? Porque no podemos admitir una teoría que explique las fuerzas de la naturaleza y deje fuera a una de esas fuerzas. Así ocurre con el Modelo Estándar que deja aparte y no incluye a la fuerza gravitatoria que está ahí, en la Naturaleza.
La teoría de supercuerdas se perfila como la teoría que tiene implicaciones si tratamos con las cosas muy pequeñas, en el microcosmos; toda la teoría de partículas elementales cambia con las supercuerdas que penetra mucho más; llega mucho más allá de lo que ahora es posible.

La topología es, el estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, ésto es, análisis de la posición.
De manera informal, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajarnos con homeomorfismos.

En cuanto a nuestra comprensión del universo a gran escala (Espacio-tiempo, galaxias, supercúmulos, el Big Bang…), creo que afectará a nuestra idea presente, al esquema que hoy rige y, como la nueva teoría, el horizonte se ampliará enormemente; el cosmos se presentará ante nosotros como un todo, con un comienzo muy bien definido y un final muy bien determinado.
Para cuando eso llegue, sabremos lo que es, como se genera y dónde están situados los orígenes de esa “fuerza”, “materia”, o, “energía” que ahora no sabemos ver para explicar el movimiento de las galaxias o la expansión del espacio mismo, y, dónde está el origen de todo, esa sustancia cósmica que puede ser la causante del universo que conocemos y también, de que podamos estar aquí para contarlo.
emilio silvera
Ago
13
Recordemos a un personaje, unos hechos.
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Personajes ilustres ~
Clasificado en Personajes ilustres ~
 Comments (1)
Comments (1)

Euclides nos presentaba un universo de espacios planos y, dos mil años más tarde, llegó Riemann y nos habló de un Universo curvo
Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.

Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.

Portada de la décimo primera edición de los “Eléments de Geométrie” de A. M. Legendre (1794)
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.
Cuando el director le preguntó: “¿hasta dónde has leído?”, el joven Riemann respondió: “este es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.
Universität Göttingen
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.


Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.
En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.
Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).
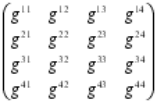
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.
Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere..
Ago
13
¡Aquellos primeros momentos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Algo de lo que pasó desde el Big Bang ~
Clasificado en Algo de lo que pasó desde el Big Bang ~
 Comments (0)
Comments (0)
Todo en el Universo tiene un principio y un final y, el mismo universo tuvo que nacer y evolucionar para que hoy podamos contemplar, mediante nuestros sofisticados telescopios, un universo en expansión lleno de galaxias que contienen estrellas nuevas y viejas estrellas, muchas de ellas rodeadas de mundos que, aún no hemos podido determinar de qué criaturas estarán poblados muchos de ellos.

¡El Universo!
Antes de alrededor de un minuto y cuarenta segundos desde el comienzo del tiempo, no hay núcleos atómicos estables. El nivel de energía en el ambiente es mayor que la energía de unión nuclear. Por consiguiente, todos los núcleos que se forman, se destruyen de rápidamente.
Alrededor de un segundo desde el comienzo del tiempo, llegamos a la época de desacoplamiento de los neutrinos. Aunque en esa época el Universo es más denso que las orcas (y tan caliente como la explosión de una bomba de hidrógeno), ya ha empezado a parecer vacío a los neutrinos. Puesto que los neutrinos sólo reaccionan a la fuerza débil, que tiene un alcance extremadamente corto, pueden escapar de sus garras y volar indefinidamente sin experimentar ninguna otra interacción.

Aunque parezca mentira, al día de hoy no sabemos, a ciencia cierta, como se formaron las galaxias
Así, emancipados, en lo sucesivo son libres de vagar por el Universo a su manera indiferente, volando a través de la mayor de la materia como sino existiese. (Diez trillones de neutrinos atravesarán sin causar daños el cerebro y el cuerpo del lector en el tiempo que le lleve leer esta frase. Y en el tiempo en que usted haya leído esta frase estarán más lejos que la Luna).
En menos de un siglo, el neutrino pasó de una partícula fantasma – propuesta en 1930 por el físico austríaco Wolfgang Pauli (1900-1958) a explicar el balance de energía en una forma de radioactividad, el llamado decaimiento beta, en una sonda capaz de escrutar el interior de estrellas y de la propia Tierra.

De esa manera, oleadas de neutrinos liberados en un segundo después del big bang persiste aún después, formando una radiación cósmica de fondo de neutrinos semejante a la radiación de fondo de microondas producida por el desacoplamiento de los fotones.
Si estos neutrinos “cósmicos” (como se los llama para diferenciarlos de los neutrinos liberados más tarde por las supernovas) pudiesen ser observador por un telescopio de neutrinos de alguna clase, proporcionarían una visión directa del Universo cuando sólo tenía un segundo.
A medida que retrocedemos en el tiempo, el Universo se vuelve más denso y más caliente, y el nivel de estructura que puede existir se hace cada vez más rudimentario.

Por supuesto, en ese tiempo, no hay moléculas, ni átomos, ni núcleos atómicos, y, a 10-6 (0.000001) de segundo después del comienzo del tiempo, tampoco hay neutrones ni protones. El Universo es un océano de quarks libres y otras partículas elementales.
Si nos tomamos el de contarlos, hallaremos que por cada mil millones de antiquarks existen mil millones y un quark. asimetría es importante. Los pocos quarks en exceso destinados a sobrevivir a la aniquilación general quark-antiquark formaran todos los átomos de materia del Universo del último día. Se desconoce el origen de la desigualdad; presumiblemente obedezca a la ruptura de una simetría materia antimateria en alguna etapa anterior.
Nos aproximamos a un tiempo en que las estructuras básicas de las leyes naturales, y no sólo las de las partículas y campos cuya conducta dictaban, cambiaron a medida que evolucionó el Universo.
La primera transición semejante se produjo en los 10-11 de segundo después del comienzo del tiempo, cuando las funciones de las fuerzas débiles y electromagnéticas se regían por una sola fuerza, la electrodébil. hay bastante energía ambiente para permitir la creación y el mantenimiento de gran de bosones w y z.


Estas partículas – las mismas cuya aparición en el acelerador del CERN verificó la teoría electrodébil – son las mediadoras intercambiables en las interacciones de fuerzas electromagnéticas y débiles, lo que las hace indistinguibles. En ese tiempo, el Universo está gobernando sólo por tres fuerzas: la gravedad, la interacción nuclear fuerte y la electrodébil.
Más atrás de ese tiempo nos quedamos en el misterio y envueltos en una gran nebulosa de ignorancia. Cada uno se despacha a su gusto para lanzar conjeturas y teorizar sobre lo que pudo haber sido. Seguramente, en el futuro, será la teoría M (de supercuerdas) la que contestará esas preguntas sin respuestas ahora.
En los 10-35 de segundo desde el comienzo del tiempo, entramos en un ámbito en el que las cósmicas son aún menos conocidas. Si las grandes teorías unificadas son correctas, se produjo una ruptura de la simetría por la que la fuerza electronuclear unificada se escindió en las fuerzas electrodébil y las fuertes. Si es correcta la teoría de la supersimetría, la transición puede haberse producido antes, había involucrado a la gravitación.
En el universo temprano la primera materia (hidrógeno y Helio) era llevada por la fuerza de gravedad a conformarse en grandes conglomerados de gas y polvo que interacioban, producían calor y formaron las primeras estrellas.
Elaborar una teoría totalmente unificada es tratar de comprender lo que ocurrió en ese tiempo remoto que, según los últimos estudios está situado entre 15.000 y 18.000 millones de años, cunado la perfecta simetría que, se pensaba, caracterizó el Universo, se hizo añicos para dar lugar a los simetrías rotas que hallamos a nuestro alrededor y que, nos trajo las fuerzas y constantes Universales que, paradójicamente, hicieron posible nuestra aparición para que , sea posible que, alguien como yo esté contando lo que pasó.
Pero hasta que no tengamos tal teoría no podemos esperar comprender lo que realmente ocurrió en ese Universo bebé. Los límites de nuestras conjeturas actuales cuando la edad del Universo sólo es de 10-43 de segundo, nos da la única respuesta de encontrarnos ante una puerta cerrada.
Del otro lado de esa puerta está la época de Plank, un tiempo en que la atracción gravitatoria ejercida por cada partícula era comparable en intensidad a la fuerza nuclear fuerte.

La fuerza nuclear fuerte hizo posible la existencia de los núcleos que atraían electrones para formar átomos
Así que, llegados a este punto podemos decir que la clave teórica que podría abrir esa puerta sería una teoría unificada que incluyese la gravitación, es decir, una teoría cuántica-gravitatoria que uniese, de una vez por todas, a Planck y Einsteins que, aunque eran muy amigos, no parecen que sus teorías (la Mecánica Cuántica) y (la Relatividad General) se lleven de maravilla.
emilio silvera
Ago
13
¡Nuestras Mentes!…¡ ¿Llegaremos a comprenderlas alguna vez?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y... ¿nosotros? ~
Clasificado en El Universo y... ¿nosotros? ~
 Comments (0)
Comments (0)

Una parte de la ciencia estudia la estructura y la evolución del Universo: La cosmología.
La cosmología observacional se ocupa de las propiedades físicas del Universo, como su composición física referida a la química, la velocidad de expansión y su densidad, además de la distribución de Galaxias y cúmulos de galaxias. La cosmología física intenta comprender estas propiedades aplicando las leyes conocidas de la física y de la astrofísica. La cosmología teórica construye que dan una descripción matemática de las propiedades observadas del Universo basadas en esta comprensión física.
La cosmología también tiene aspectos filosóficos, o incluso teológicos, en el sentido de que trata de comprender por qué el Universo tiene las propiedades observadas. La cosmología teórica se basa en la teoría de la relatividad , la teoría de Einstein de la gravitación. De todas las fuerzas de la naturaleza, la gravedad es la que tiene efectos más intensos a escalas y domina el comportamiento del Universo en su conjunto.
El espacio-tiempo, la materia contenida en el Universo con la fuerza gravitatoria que , los posibles agujeros de gusano y, nuestras mentes que tienen conocimientos de que todo esto sucede o puede suceder. De manera que, nuestro consciente (sentimos, pensamos, queremos obrar con conocimiento de lo que hacemos), es el elemento racional de personalidad humana que controla y reprime los impulsos del inconsciente, para desarrollar la capacidad de adaptación al mundo exterior.


Al ser conscientes, entendemos y aplicamos nuestra razón natural para clasificar los conocimientos que adquirimos mediante la experiencia y el estudio que aplicamos a la realidad del mundo que nos rodea. Claro que, no todos podemos percibir la realidad de la misma manera, las posibilidades existentes de que el conocimiento de esa realidad, responda exactamente a lo que ésta es en sí, no parece .

Descartes, Leibniz, Locke, Berkeley, Hume (que influyó decisivamente en Kant), entre otros, construyeron una base que tomó fuerza en Kant, para quien el conocimiento arranca o nace de nuestras experiencias sensoriales, es decir, de los datos que nos suministra nuestros cinco sentidos, pero no todo en él procede de esos datos. Hay en nosotros dos fuentes o potencias distintas que nos capacitan , y son la sensibilidad (los sentidos) y el entendimiento (inteligencia). Esta no puede elaborar ninguna idea sin los sentidos, pero éstos son inútiles sin el entendimiento.
A todo esto, para mí, el conocimiento está inducido por el . La falta y ausencia de interés aleja el conocimiento. El interés puede ser de distinta índole: científico, social, artístico, filosófico, etc. (La gama es tan amplia que existen conocimientos de todas las posibles vertientes o direcciones, hasta tal punto es así que, nunca nadie lo podrá saber todo sobre todo). Cada uno de nosotros puede elegir sobre los conocimientos que prefiere adquirir y la elección está adecuada a la conformación individual de la sensibilidad e inteligencia de cada cual.

Siempre sentimos curiosidad por saber como era el mundo y qué había en los cielos
También se da el caso de personas que prácticamente, por cuestiones genéticas o de otra índole, carecen de cualquier por el conocimiento del mundo que les rodea, sus atributos sensoriales y de inteligencia funcionan a tan bajo rendimiento que, sus comportamientos son casi-animales (en el sentido de la falta de racionalidad), son guiados por la costumbre y las necesidades primarias: comer, dormir…
El polo opuesto lo encontramos en múltiples ejemplos de la historia de la ciencia, donde personajes como Newton, Einstein, Riemann, Ramanujan y tantos otros (cada uno en su ámbito del conocimiento), dejaron la muestra al mundo de su genio .
Pero toda la realidad está encerrada en una enorme burbuja a la que llamamos Universo y que guarda todos los misterios y secretos que nosotros, seres racionales y conscientes, perseguimos para saber, ese preciado bien que no todos podemos alcanzar.


A la conciencia nos grita
Todo el mundo sabe lo que es la conciencia; es lo que nos abandona cada noche cuando nos dormimos y reaparece a la mañana siguiente cuando nos despertamos. Esta engañosa simplicidad me recuerda lo que William James escribió a finales del siglo XIX sobre la atención:”Todo el mundo sabe lo que es la atención; es la toma de posesión por la mente, de una forma clara e intensa, de un hilo de pensamiento de entre simultáneamente posibles”. Más de cien años más tarde somos muchos los que creemos que seguimos sin tener una comprensión de fondo ni de la atención, ni de la conciencia que, desde luego, no creo que se marche cuando dormimos, ella no nos deja nunca.
La falta de comprensión ciertamente no se debe a una falta de atención en los círculos filosóficos o científicos. Desde que René Descartes se ocupara del problema, pocos han los temas que hayan preocuado a los filósofos tan persistentemente como el enigma de la conciencia.
Para Descartes, como para más de dos siglos después, ser consciente era sinónimo de “pensar”: el hilo de pensamiento de James no era otra cosa que una corriente de pensamiento. El cogito ergo sum, “pienso, luego existo”, que formuló Descartes como fundamento de su filosofía en Meditaciones de prima philosophía, era un reconocimiento explícito del papel central que representaba la conciencia con respecto a la ontología (qué es) y la epistemología (qué conocemos y cómo le conocemos).

Claro que tomado a pie juntillas, “soy consciente, luego existo”, nos conduce a la creencia de que nada existe más allá o fuera de la propia conciencia y, por mi parte, no estoy de acuerdo. Existen muchísimas cosas y hechos que no están al alcance de mi conciencia. Unas veces por imposibilidad física y otras por imposibilidad intelectual, lo es que son muchas las cuestiones y las cosas que están ahí y, sin embargo, se escapan a mi limitada conciencia.
Todo el entramado existente alrededor de la conciencia es de una complejidad enorme, de hecho, conocemos mejor el funcionamiento del Universo que el de nuestros propios cerebros. ¿Cómo surge la conciencia como resultado de procesos neuronales particulares y de las interacciones entre el cerebro, el cuerpo y el mundo? ¿Cómo pueden explicar estos procesos neuronales las propiedades esenciales de la experiencia consciente ?
Cada uno de los estados conscientes es unitario e indivisible, pero al mismo tiempo cada persona puede elegir entre un ingente de estados conscientes distintos.

Sherrington
Muchos han los que han querido explicar lo que es la conciencia. En 1.940, el gran neurofisiólogo Charles Sherrington lo intento y puso un ejemplo de lo que él pensaba sobre el problema de la conciencia. Unos pocos años más tarde también lo intentaron otros y, antes, el mismo Bertrand Russell hizo lo propio, y, en todos los casos, con más o menos acierto, el resultado no fue satisfactorio, por una sencilla razón: nadie sabe a ciencia cierta lo que en verdad es la conciencia y cuales son sus verdaderos mecanismos; de hecho, Russell expresó su escepticismo sobre la capacidad de los filósofos para alcanzar una respuesta:
“Suponemos que un proceso fisico da comienzo en un objeto visible, viaja hasta el ojo, donde se convierte en otro proceso físico en el nervio óptico y, finalmente, produce algún efecto en el cerebro al mismo tiempo que vemos el objeto donde se inició el proceso; pero este proceso de ver es algo “mental”, de naturaleza totalmente distinta a la de los procesos físicos que lo preceden y acompañan. Esta concepción es tan extraña que los metafísicos han inventado toda suerte de teorías con el fin de sustituirla con algo menos increíble”.
Está claro que en lo más profundo de ésta consciencia que no conocemos, se encuentran todas las respuestas a las preguntas planteadas o requeridas mediante interrogantes que nadie ha sabido despejar. Cada cual sigue en “su mundo” que, necesariamente, no tiene que coincidir con el mundo real en el que estamos. No todos percibimos las cosas de la misma manera.

Al comienzo mencionaba el cosmos y la gravedad junto con la consciencia y, en realidad, con más o menos acierto, de lo que estaba tratando era de hacer ver que todo ello, es la misma cosa. Universo-Galaxia-Mente. Nada es independiente en un sentido global, sino que son de un todo y están estrechamente relacionados.

Una Galaxia es simplemente una parte pequeña del Universo, nuestro planeta es, una mínima fracción infinitesimal de esa Galaxia, y, nosotros mismos, podríamos ser comparados (en a la inmensidad del cosmos) con una colonia de bacterias pensantes e inteligentes. Sin embargo, todo forma parte de lo mismo y, aunque pueda dar la sensación engañosa de una cierta autonomía, en realidad todo está interconectado y el funcionamiento de una cosa incide directamente en las otras.
Pocas dudas pueden caber a estas alturas de que, el hecho de que podamos estar hablando de estas cuestiones, es un milagro en sí .
Después de millones y millones de años de evolución, se formaron las conciencias primarias que surgieron en los animales conciertas estructuras cerebrales de cierta (aunque limitadas) complejidad que, podían ser capaces de construir una escena mental, pero con capacidad semántica o simbólica muy limitada y careciendo de un verdadero lenguaje.
La conciencia de orden (que floreció en los humanos y presupone la coexistencia de una conciencia primaria) viene acompañada de un sentido de la propia identidad y de la capacidad explícita de construir en los estados de vigilia escenas pasadas y futuras. Como mínimo, requiere una capacidad semántica y, en su forma más desarrollada, una capacidad lingüística.

Los procesos neuronales que subyacen en nuestro cerebro son en realidad desconocidos y, aunque son muchos los y experimentos que se están realizando, su complejidad es tal que, de momento, los avances son muy limitados. Estamos tratando de conocer la máquina más compleja y perfecta que existe en el Universo.
Si eso es así, resultará que después de todo, no somos tan insignificantes como en un principio podría parecer, y solo se trata da tiempo. En su momento y evolucionadas, nuestras mentes tendrán un nivel de conciencia que estará más allá de las percepciones físicas tan limitadas. Para entonces, sí estaremos totalmente integrados y formando parte, como un todo, del Universo que ahora presentimos.
El carácter de la conciencia me hace adoptar una posición que me lleva a decidir que no es un objeto, sino un proceso y que, desde este punto de , puede considerarse un ente digno del estudio científico perfectamente legítimo.

Es tan comùn y abundante que no le damos la importancia que realmente tiene para la vida
La conciencia plantea un problema especial que no se encuentra en otros dominios de la ciencia. En la Física y en la Química se suele explicar unas entidades determinadas en función de otras entidades y leyes. Podemos describir el agua con el lenguaje ordinario, pero podemos igualmente describir el agua, al menos en principio, en términos de átomos y de leyes de la mecánica cuántica. Lo que hacemos es conectar dos niveles de descripción de la misma entidad externa (uno común y otro científico de extraordinario poder explicativo y predictivo. Ambos niveles de descripción) el agua líquida, o una disposición particular de átomos que se comportan de acuerdo con las leyes de la mecánica cuántica (se refiere a una entidad que está fuera de nosotros y que supuestamente existe independientemente de la existencia de un observador consciente.

En el caso de la conciencia, sin embargo, nos encontramos con una simetría. Lo que intentamos no es simplemente comprender de qué manera se puede explicar las conductas o las operaciones cognitivas de otro ser humano en términos del funcionamiento de su cerebro, por difícil que esto parezca. No queremos simplemente conectar una descripción de algo externo a nosotros con una descripción científica más sofisticada. Lo que realmente queremos hacer es conectar una descripción de algo externo a nosotros (el cerebro), con algo de nuestro interior: una experiencia, nuestra propia experiencia individual, que nos acontece en tanto que observadores conscientes. Intentamos meternos en el interior o, en la atinada ocurrencia del filósofo Tomas Negel, qué se siente al ser un murciélago. Ya sabemos qué se siente al ser nosotros mismos, qué significa ser nosotros mismos, pero queremos explicar por qué somos conscientes, saber qué es ese “algo” que no s hace ser como somos, explicar, en fin, cómo se generan las cualidades subjetivas experienciales. En suma, deseamos explicar ese “Pienso, luego existo” que Descartes postuló como evidencia primera e indiscutible sobre la cual edificar toda la filosofía.
Ninguna descripción, por prolija que sea, logrará nunca explicar cabalmente la experiencia subjetiva. Muchos filósofos han utilizado el ejemplo del color para explicar este punto. Ninguna explicación científica de los mecanismos neuronales de la discriminación del color, aunque sea enteramente satisfactorio, bastaría para comprender cómo se siente el proceso de percepción de un color. Ninguna descripción, ninguna teoría, científica o de otro tipo, bastará nunca para que una daltónica consiga experimentar un color.

En un experimento mental filosófico, Mary, una neurocientífica del futuro daltónica, lo sabe todo acerca del visual y el cerebro, y en particular, la fisiología de la discriminación del color. Sin embargo, cuando por fin logra recuperar la visión del color, todo aquel conocimiento se revela totalmente insuficiente comparado con la auténtica experiencia del color, comparado con la sensación de percibir el color. John locke vio claramente este problema hace mucho tiempo.
Pensemos por un momento que tenemos un amigo ciego al que contamos lo que estamos viendo un día soleado del mes de abril: El cielo despejado, limpio y celeste, el Sol allí arriba esplendoroso y cegador que nos envía su luz y su calor, los árabes y los arbustos llenos de flores de mil colores que son asediados por las abejas, el aroma y el rumor del río, cuyas aguas cantarinas no cesan de correr transparentes, los pajarillos de distintos plumajes que lanzan alegres trinos en sus vuelos por el ramaje que se mece movido por una brisa suave, todo esto lo contamos a nuestro amigo ciego que, si de pudiera ver, comprobaría que la experiencia directa de sus sentidos ante tales maravillas, nada tiene que ver con la pobreza de aquello que le contamos, por muy hermosas palabras que para hacer la descripción empleáramos.

La mente humana es tan compleja que, no todos ante la misma cosa, vemos lo mismo. Nos enseñan figuras y dibujos y nos piden que digamos (sin pensarlo) la primera cosa que nos sugiere. De entre personas solo coinciden tres, los otro siete divergen en la apreciación de lo que el dibujo o la figura les sugiere.
Esto nos viene a demostrar la individualidad de pensamiento, el libre albedrío para decidir. Sin embargo, la misma , realizada en grupos de conocimientos científicos similares y específicos: Físicos, matemáticos, químicos, etc. hace que el número de coincidencias sea más elevada, más personas ven la misma respuesta al problema planteado. Esto nos sugiere que, la mente, está en un estado virgen que cuenta con todos los elementos necesarios para dar respuestas pero que necesita experiencias y aprendizaje para desarrollarse.
¿ Debemos concluir entonces que una explicación científica satisfactoria de la conciencia queda para siempre fuera de nuestro alcance? ¿O es de manera posible romper esa barrera, tanto teórica como experimental, para resolver las paradojas de la conciencia?

Todavía no sabemos encajar las piezas
La respuesta a estas y otras preguntas, en mi opinión, radica en reconocer nuestras limitaciones actuales en este del conocimiento complejo de la mente, y, como en la Física cuántica, existe un principio de incertidumbre que, al menos de momento (y creo que en muchos cientos de años), nos impide saberlo todo sobre los mecanismos de la conciencia y, aunque podremos ir contestando a preguntas parciales, alcanzar la plenitud del conocimiento total de la mente no será nada sencillo, entre otras razones está el serio inconveniente que su nosotros mismos, ya que, con nuestro que hacer podemos, en cualquier momento, provocar la propia destrucción.
Una cosa si está clara: ninguna explicación científica de la mente podrá nunca sustituir al fenómeno real de lo que la propia mente pueda .

¿ Cómo se podría comparar la descripción de un con sentirlo, vivirlo física y sensorialmente hablando ?
Hay cosas que no pueden ser sustituidas, por mucho que los analistas y especialistas de publicidad y márketin se empeñen, lo auténtico siempre será único. Es curioso cómo funciona la Naturaleza. Si miramos unos millones de protones, electrones o neutrones, no podemos ver ninguna diferencia en ninguno de ellos, todos son exactamente iguales. Sin embargo, nosotros los Humanos, somos siete mil millones y, aunque parecidos, nunca podremos encontrar a dos seres iguales, ni físicamente ni mentalmente tampoco, Cada uno de nosotros tiene su propio mundo en su Mente.
emilio silvera
Ago
12
Nebulosas Planetarias y estrellas enanas blancas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Nebulosas y estrellas ~
Clasificado en Nebulosas y estrellas ~
 Comments (0)
Comments (0)

NGC 2392 es una nebulosa planetaria en la constelación de Gérminis
En la imagen del día del Blog, hoy aparece la Nebulosa del Esquimal o del Payaso, NGC 2392, que forma un conjunto vistoso. Por su curiosa apariencia, que recuerda a la cara de una persona rodeada por una capucha, recibe también los nombres de Nebulosa Esquimal. Se encuentra, según autores, a unos 3000 o 5000 años-luz de la Tierra.
La edad de NGC 2392 se estima en unos 10.000 años, y está compuesta por dos lóbulos elípticos de materia saliendo de la estrella moribunda. Desde nuestra perspectiva, unos de los lóbulos está delante del otro.

Se cree que la forma de la nebulosa se debe a un anillo de material denso alrededor del ecuador de la estrella expulsado durante la fase de gigante roja. Este material denso es arrastrado a una velocidad de 115.000 km/h., impidiendo que el viento estelar, que posee una velocidad mucho mayor, empuje la materia a lo largo del ecuador. Por el contrario, este viento de gran velocidad (1,5 millones de km/h) barre material por encima y debajo de la estrella, formando burbujas alargadas. Estas burbujas, de 1 año luz de longitud y la mitad de anchura, tienen filamentos de materia más densa. No obstante, las líneas que van de dentro a afuera en el anillo exterior (en la capucha) no tienen todavía explicación, si bien su origen puede deberse a la colisión entre gases de baja y alta velocidad.
La Nebulosa del Esquimal fue descubierta por William Herschel el 17 de enero de 1787.

La Nebulosa Reloj de Arena
Una nebulosa planetaria es una nebulosa de emisión consistente en una envoltura brillante en expansión de plasma y gas ionizado, expulsada durante la fase de rama asintótica gigante que atraviesan las estrellas gogantes rojas en los últimos momentos de sus vidas.
Las nebulosas planetarias son objetos de gran importancia en astronpmía, debido a que desempeñan un papel crucial en la evolución química de las Galaxias, devolviendo al medio interestelar metales pesados y otros productos de la nucleosíntesis de las estrellas (como Carbono, Nitrógeno, xígeno, Calcio… y otros). En galaxias lejanas, las nebulosas planetarias son los únicos objetos de los que se puede obtener información útil acerca de su composición química.
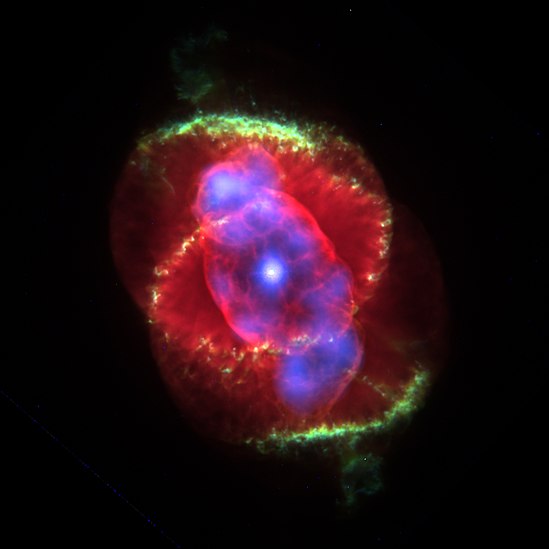
La gama y diseños de Nebulosas Planetarias es de muy amplio abanico y, en esa familia de Nubulosas podemos admirar y asombrarnos con algunas que, como la famosa Ojo de Gato (arriba), nos muestra una sinfonía de arquitectónica superpuesta que ni la mente del más avispado arquitecto habría podido soñar.

Una enana blanca es una pequeña y densa estrella que es el resultado final de la evolución de todas las estrellas (por el ejemplo el Sol), excepto las muy masivas. Según todos los estudios y observaciones, cálculos, modelos de simulación, etc., estas estrellas se forman cuando, al final de la vida de las estrellas medianas, agotan el combustible de fusión nuclear, se produce el colapso de sus núcleos estelares, y quedan expuestas, cuando las partes exteriores de la estrella son expulsadas al espacio interestelar formar una Nebulosa Planetaria. En el centro de la Nebulosa, queda denudo un puntito blanco que es, la estrella enana blanca.
El Núcleo se contrae bajo su propia gravedad hasta que, habiendo alcanzado un tamaño similar al de la Tierra , se ha vuelto tan densa (5 x 10 ^8 Kg/m3) que sólo evita su propio colapso por la preseión de degeneración de los electrones ( saben los electrones son fermiones que estando sometidos al Principio de exclusión de Pauli, no pueden ocupar niguno de ellos el mismo lugar de otro al tener el mismo número cuántico y, siendo así, cuando se juntan demasiado, se degeneran y comienzan una frenética carrera que, en su intensidad, , incluso frenar la implosión de una estrella -como es el caso de las enanas blancas).
Las enanas blancas se forman con muy altas temperaturas superficiales (por encima de los 10 000 K) debido al calor atrapados en ellas, y liberado por combustiones nucleares previas y por la intensa atracción gravitacional que sólo se ve frenada por la degeneración de los electrones que, finalmente, la estabilizan como estrella enana blanca.
tipo de estrellas, con el paso del tiempo, se enfrían gradualmente, volviéndose más débiles y rojas. Las enanas blancas pueden constituir el 30 por ciento de las estrellas de la vecindad solar, aunque debido a sus bajas luminosidades de 10 ^-3 – 10 ^-4 veces la del Sol, pasan desapercibidas. La máxima máxima posible de una enana blanca es de 1,44 masas solares, el límite de Shandrasekhar. Un objeto de masa mayor se contraería aún más y se convertiría en una estrella de neutrones o, de tener mucha masa, en un agujero negro.

Las enanas blancas son estrellas calientes y pequeñas, generalmente del tamaño de la Tierra, por lo que su luminosidad es muy baja. Se cree que las enanas blancas son los residuos presentes en el centro de las nebulosas planetarias. Dicho de otra manera, las enanas blancas son el núcleo de las estrellas de baja masa que quedan después de que la envoltura se ha convertido en una nebulosa planetaria.
El núcleo de una enana blanca consiste de material de electrones degenerados. Sin la posibilidad de tener nuevas reacciones nucleares, y probablemente después de haber perdido sus capas externas debido al viento solar y la expulsión de una nebulosa planetaria, la enana blanca se contrae debido a la fuerza de gravedad. La contracción hace que la densidad en el núcleo aumente hasta que se den las necesarias para tener un material de electrones degenerados. Este material genera presión de degeneración, el cual contrarresta la contracción gravitacional.
Al ser estudiadas más a fondo las propiedades de las enanas blancas se encontró que al aumentar su masa, su radio disminuye. A partir de esto es que se encuentra que hay un límite superior la masa de una enana blanca, el cual se encuentra alrededor de 1.4 masas solares (MS). Si la masa es superior a 1.4 MS la presión de degeneración del núcleo no es suficiente detener la contracción gravitacional. Este se llama el límite de Chandrasekhar.
Debido a la existencia de este límite es que las estrellas de entre 1.4 MS y 11 MS deben perder masa para poder convertirse en enanas blancas. Ya explicamos que dos medios de pérdida de masa son los vientos estelares y la expulsión de nebulosas planetarias. Sin embargo, existen otras posiblidades que se puedan dar en este tipo de estrellas que son muy densas. Por ejemplo, si cerca de alguna de ellas reside otra estrella que esté lo bastante cerca, la enana blanca, poco a poco, puede ir robándole masa a la estrela compañera hasta que, llegado a un punto, ella misma se recicla y se convierte en una estrella de Neutrones.

Después de que una estrella se ha convertido en enana blanca, lo más probable es que su destino sea enfriarse y perder brillo. Debido a que las enanas blancas tienen una baja luminosidad, pierden energía lentamente, por lo que pueden permanecer en etapa en el orden de años. Una vez que se enfrían, se vuelven rocas que se quedan vagando por el Universo. Este es el triste destino de nuestro Sol.
La detección de enanas blancas es difícil, ya que son objetos con un brillo muy débil. Por otro lado, hay ciertas diferencias en las enanas blancas según su masa. Las enanas blancas menos masivas sólo alcanzan a quemar hidrógeno en helio. Es decir, el núcleo de la estrella nunca se comprime lo suficiente como alcanzar la temperatura necesaria para quemar helio en carbono. Las enanas blancas más masivas sí llevan a cabo reacciones nucleares de elementos más pesados, es decir, en su núcleo podemos encontrar carbono y oxígeno.
Allá por el año 1908, siendo Chandrasekhar un avanzado estudiante de física, vivía en Madrás, en la Bahía de Bengala (En cuyo Puerto trabajó Ramanujan), y, estando en aquella ciudad el célebre científico Arnold Sommerfeld, le pidió audiciencia y se pudo entrevistar con él que, le vino a decir que la física que estudiaba estaba pasada, que se estaban estudiando nuevos caminos de la física y, sobre todo, uno a cuya teoría se la llamaba mecánica cuántica que podía explicar el comportamiento de lo muy pequeño.

Cuando se despidieron Sommerfeld dio a Chandrasekhar la prueba de imprenta de un artículo técnico que acaba de escribir. Contenía una derivación de las leyes mecanocuánticas que gobiernan grandes conjuntos de electrones comprimidos en volúmenes pequeños, por ejemplo ( este caso) en una estrella enana blanca.
A partir de aquel artículo, Chandrasekhar buscó más información y estudió estos fenómenos estelares que desembocaban en enanas blancas. Este tipo de estrella habían descuibiertas por las astrónomos a través de sus telescopios. Lo misterioso de las enanas blancas era su densidad extraordinariamente alta de la materia en su interior, una densidad muchísimo mayor que la de cualquier otra cosa que los seres humanos hubieran encontrado antes. Chandrasekhar no tenía forma de saberlo cuando abrió un libro de Eddintong que versaba sobre la materia, pero la lucha por desvelar el misterio de alta densidad le obligaría fibnalmente a él y a Eddintong a afrontar la posibilidad de que las estrellas masivas, cuando mueren, pudieran contraerse para formar agujeros negros.

De las enanas blancas más conocidas y cercanas, tenemos a Sirio B. Sirio A y Sirio B son la sexta y la séptima estrellas en orden de proximidad a la Tierra, a 8,6 años-luz de distancia, y Sirio es la estrella más brillante en nuestro cielo. Sirio B orbita en torno a Sirio de la misma manera que lo hace la Tierra alrededor del Sol, pero Sirio B tarde 50 años en completar una órbita a Sirio y la Tierra 1 año al Sol.
Eddintong describía como habían estimado los astrónomos, a partir de observaciones con telescopios, la masa y la circunferencia de Sirio B. La masa era de 0,85 veces la masa del Sol; la circunferencia media 118.000 km. Esto significaba que la densidad media de Sirio B era de 61.000 gramos por centímetro cúbico, es decir 61.000 veces mayor que la densidad del agua. “Este argumento se conoce ya hace algunos años -nos decía Eddintong-” Sin embargo, la mayoría de los astrónomos de aquel tiempo, no se tomaban en serio tal densidad, Sin embargo, si hubieran conocido la verdad que conocemos: (Una masa de 1,05 soles, una circunferencia de 31.000 km y una densidad de 4 millones de gramos por cm3), la habrían considerado aún más absurda.

Arriba la famosa Nebulosa planetaria ojo de Gato que, en su centro luce una estrella enana blanca de energéticas radiaciones en el ultravioleta y que, a medida que se vaya enfriando, serán de rayos C y radio que, dentro de unos 100 millones de años vieja y fria, será más rojiza y se habrá convertido en un cadáver estelar.
Aquellos trabajos de Chandraskar y Eddintong desembocaron en un profundo conocimiento de las estrellas de neutrones y, se llego a saber el por qué conseguian el equilibrio que las estabilizaba a través de la salvación que, finalmente encontraban, en la mecánica cuántica, cuando los electrones degenerados por causa del Principio de esclusión de Pauli, no dejaban que la fuerza gravitatoria continuara el proceso de contracción de la estrella y así, quedaba estabilizada como estrella de neutrones.
De la misma manera, se repetía el proceso estrellas más masivas que, no pudiendo ser frenadas en su implosión gravitatoria por la degeneración de los electrones, sí que podia frenarse la Gravedad, mediante la degeneración de los Neutrones. Cuando esa estrella más masiva se contraía más y más, el Principio de exclusión de pauli que impide que los fermiones estén juntos, comenzaba su trabajo e impedía que los neutrones (que son fermiones), se juntaran más, entonces, como antes los electrones, se degeneraban y comenzaban a moverse con velocidades relativistas y, tan hecho, impedía, por sí mismo que la Gravedad consiguiera comprimir más la masa de la estrella que, de manera, quedaba convertida, finalmente, en una Estrella de Neutrones.

Al formarse la estrella de neutrones la estrella se colapsa hasta formar una esfera perfecta con un radio de tan solo unos 10 kilómetros. En este punto la presión neutrónica de Fermi resultante compensa la fuerza gravitatoria y estabiliza la estrella de neutrones. Apenas una cucharilla del material que conforma una estrella de neutrones tendría una masa superior a 5 x 10 ^12 kilogramos.
Los modelos de estrellas de neutrones que se han logrado construir utilizando las leyes físicas presentan varias capas. Las estrella de neutrones presentarían una corteza de hierro muy liso de, aproximadamente, un metro de espesor. Debajo de corteza, prácticamente todo el material está compuesto por núcleos y partículas atómicas fuertemente comprimidos formando un “cristal” sólido de materia nucleica.

Son objetos extremadamente pequeños u densos que surgen cuando estrellas masivas sufren una explosión supernova del II, el núculeo se colapsa bajo su propia gravedad y puede llegar hasta una densidad de 10 ^17 Kg/m3. Los electrones y los protones que están muy juntos se fusionan y forman neutrones. El resultado final consiste solo en neutrones, cuyo material, conforma la estrella del mismo . Con una masa poco mayor que la del Sol, tendría un diámetro de sólo 30 Km, y una densidad mucho mayor que la que habría en un terrón de azúcar con una masa igual a la de toda la humkanidad. Cuanto mayor es la masa de una estrella de neutrones, menor será su diámetro. Está compuesta por un interior de neutrones superfluidos (es decir, neutrones que se comportan como un fluido de viscosidad cero), rodeado por más o menos una corteza sólida de 1 km de grosor compuesta de elementos como el hierro. Los púlsares son estrellas de neutrones magnetizadas en rotación. Las binarias de rayos X masivas también se piensan que contienen estrellas de neutrones.
Todos aquellos argumentos sobre el comportamiento de las enanas blancas vinieron a desembocar en la paradoja de Edddintong que, en realidad, fue resuelta por el Joven Chandrasekhar en el año 1925 al leer un artículo de R.H. Fowler “Sobre la materia densa”. La solución residía en el fallo de las leyes de la física que utilizaba Eddintong. Dichas leyes debían ser reemplazadas por la nueva mecánica cuántica, que describía la presión en el interior de Sirio B y otras enanas blancas como debida no al calor sino a un fenómeno mecanocuántico : los movimientos degenerados de los electrones, también llamado degeneración electrónica.
La degeneración electrónica es algo muy parecido a la claustrofia humana. Cuando la materia es comprimida hasta una densidad 10.000 veces mayor que la de una roca, la nube de electrones en torno a cada uno de sus núcleos atómicos se hace 10.000 veces más condensada, Así, cada electrón queda confinado en una “celda” con un volumen 10.000 veces menor que el volumen en el que previamente podía moverse. Con tan poco espacio disponible, el electrón, como nos pasaría a cualquiera de nosotros, se siente incómodo, siente claustrofobia y comienza a agitarse de manera incontrolada, golpeando con enorme fuerza las paredes de las celdas adyacentes. Nada puede deternerlo, el electrón está obligado a ello por las leyes de la mecánica cuántica. Esto está producido por el Principio de esclusión de Pauli que impide que dos fermiones estén juntos, así que, fuerza es, la que finalmente posibilita que la estrella que se comprime más y más, quede finalmente, constituida estable como una enana blanca.
emilio silvera
















 Totales: 75.354.217
Totales: 75.354.217 Conectados: 49
Conectados: 49