jueves, 21 de noviembre del 2024 Fecha
Ir a la página principal Ir al blog

IMPRESIÓN NO PERMITIDA - TEXTO SUJETO A DERECHOS DE AUTOR



 

«
»

Sep

21

De la vida y la muerte de las partículas y…otros

Autor por Emilio Silvera    ~    Archivo Clasificado en Física Cuántica    ~    Comentarios Comments (0)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

 «

 

 

Por aquel tiempo pudimos leer en la prensa de todo el mundo:  ESTOCOLMO, Suecia.- El premio Nobel de Física (2.008) fue atribuido hoy al norteamericano Yoichiro Nambu y a los japoneses Makoto Kobayashi y Toshihide Maskawa por sus trabajos separados sobre la física de las partículas que mejoraron la comprensión de la materia, Demos un repaso hoy aquí a esos componentes de la materia, y, profundicemos en sus propiedades., en sus “vidas”.

 

             Todo lo que vemos, está formado por partículas elementales

Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.

También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, ksi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales manera de desintegración, veríamos como difieren las unas de las otras.

Quarks Antiquarks
Nombre Símbolo[1] Generación Carga eléctrica
(e)		 Masa en reposo
(MeV/c²)		 Nombre Símbolo Generación Carga eléctrica
(e)		 Masa en reposo
(MeV/c²)
Arriba 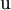\mathrm{u}\,\! Primera 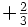\begin{matrix} +\frac{2}{3} \end{matrix} — Antiarriba 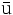\mathrm{\bar{u}}\,\! Primera 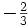\begin{matrix} -\frac{2}{3} \end{matrix} —
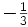Abajo \mathrm{d}\,\! Primera \begin{matrix} -\frac{1}{3} \end{matrix} — Antiabajo 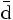\mathrm{\bar{d}}\,\! Primera \begin{matrix} +\frac{1}{3} \end{matrix} —
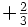Encanto \mathrm{c}\,\! Segunda \begin{matrix} +\frac{2}{3} \end{matrix} — Antiencanto 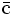\mathrm{\bar{c}}\,\! Segunda 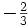\begin{matrix} -\frac{2}{3} \end{matrix} —
Extraño 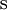\mathrm{s}\,\! Segunda 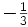\begin{matrix} -\frac{1}{3} \end{matrix} — Antiextraño 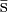\mathrm{\bar{s}}\,\! Segunda \begin{matrix} +\frac{1}{3} \end{matrix} —
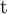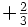Cima \mathrm{t}\,\! Tercera \begin{matrix} +\frac{2}{3} \end{matrix} — Anticima 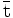\mathrm{\bar{t}}\,\! Tercera 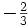\begin{matrix} -\frac{2}{3} \end{matrix} —
Fondo 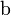\mathrm{b}\,\! Tercera 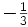\begin{matrix} -\frac{1}{3} \end{matrix} — Antifondo 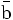\mathrm{\bar{b}}\,\! Tercera \begin{matrix} +\frac{1}{3} \end{matrix} —
Las iniciales de los símbolos los toma del inglés: u: up, arriba; d: down, abajo; c: charmed, encantado; s: strange, extraño; t: top, alto, superior, cima; b: bottom bajo, fondo.

Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.

Diagrama de partículas elementales

Todas las partículas elementales vistas hasta ahora en esta serie, incluido el neutrino. Claro que, aquí no está todavía el Bosón de Higgs que será confirmado en breve…al parecer. Esas son las últimas noticias, el Bosón de Higgs está “casi” localizado y sólo está a la espera de confirmar el hallazgo no una, sino miles de veces.

CMS detector
The CMS detector.Image © CERN
ATLAS detector
The ATLAS detector. Image © CERN

Por fin, los físicos empiezan a recoger los frutos de una búsqueda que dura ya casi cincuenta años. Dos de los principales detectores del LHC, el gran acelerador europeo de partículas (el Atlas y el muones“>CMS) han encontrado señales que podrían delatar la presencia del esquivo Higgs“>bosón de Higgs, la última particula subatómica que queda por descubrir para completar el Modelo Estandar de la Física y la que encierra, además, el secreto de por qué las demás partículas tienen masa.

Pero sigamos. ¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una colisión entre un prtón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.

 

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Leptones cargados Neutrinos
Nombre Símbolo Carga Masa en reposo Nombre Símbolo Carga Masa en reposo
1ª generación Electrón 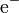\mathrm{e^-}\,\! −1 0,511
\mathrm{\nu_e}\,\! 0 < 3·10−6
Positrón 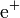\mathrm{e^+}\,\! +1 Neutrino electrónico
 \mathrm{\overline{\nu_e}} 0
2ª generación Muón 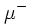\mathrm{\mu^-}\,\! −1 105,658 Neutrino muónico 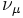\mathrm{\nu_\mu}\,\! 0 < 0,19
Antimuón \mathrm{\mu^+}\,\! +1 Antineutrino muónico 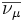\mathrm{\overline{\nu_\mu}} 0
3ª generación Tauón \mathrm{\tau^-}\,\! −1 1776,99 Neutrino tauónico \mathrm{\nu_\tau}\,\! 0 < 18,2
Antitauón \mathrm{\tau^+}\,\! +1 Antineutrino tauónico 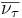\mathrm{\overline{\nu_\tau}} 0

En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas  experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.

Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Bariones

 

Partícula Símbolo[1] Quarks[2] Spin Masa en reposo
(MeV/c²)		 S C B Vida media
(s)		 Desintegraciones más importantes
Protón 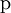\mathrm{p}\,\! \mathrm{uud}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 938,27 0 0 0 Estable [3] —
Neutrón 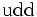\mathrm{n}\,\! \mathrm{udd}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 939,56 0 0 0 885,7 [4] \begin{matrix} {}_{n\,\rightarrow\,p + e^- + \bar{\nu}_e} & {}_{100%} \end{matrix}
Delta doble positiva 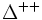\mathrm{\Delta^{++}}\,\! \mathrm{uuu}\,\! \begin{matrix} \frac{3}{2} \end{matrix} ≈1.232 0 0 0 6·10-24 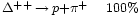\begin{matrix} {}_{\Delta^{++}\,\rightarrow\,p + \pi^+} & {}_{100%} \end{matrix}
Delta positiva \mathrm{\Delta^+}\,\! \mathrm{uud}\,\! \begin{matrix} \frac{3}{2} \end{matrix} ≈1.232 0 0 0 6·10-24 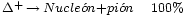\begin{matrix} {}_{\Delta^{+}\,\rightarrow\,Nucle\acute{o}n + pi\acute{o}n} & {}_{100%} \end{matrix}
Delta neutra 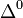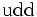\mathrm{\Delta^0}\,\! \mathrm{udd}\,\! \begin{matrix} \frac{3}{2} \end{matrix} ≈1.232 0 0 0 6·10-24 \begin{matrix} {}_{\Delta^{0}\,\rightarrow\,Nucle\acute{o}n + pi\acute{o}n} & {}_{100%} \end{matrix}
Delta negativa 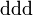\mathrm{\Delta^{-}}\,\! \mathrm{ddd}\,\! \begin{matrix} \frac{3}{2} \end{matrix} ≈1.232 0 0 0 6·10-24 \begin{matrix} {}_{\Delta^{-}\,\rightarrow\,n + \pi^-} & {}_{100%} \end{matrix}
Lambda neutra 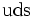\mathrm{\Lambda^0}\,\! \mathrm{uds}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.115,68 −1 0 0 2,63·10-10 \begin{matrix} {}_{\Lambda^{0}\,\rightarrow\,p + \pi^-} & {}_{63,9%} \\ {}_{\Lambda^{0}\,\rightarrow\,n + \pi^0} & {}_{35,8%} \end{matrix}
Sigma positiva 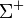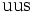\mathrm{\Sigma^+}\,\! \mathrm{uus}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.189,37 −1 0 0 8,01·10-11 \begin{matrix} {}_{\Sigma^{+}\,\rightarrow\,p + \pi^0} & {}_{51,57%} \\ {}_{\Sigma^{+}\,\rightarrow\,n + \pi^+} & {}_{48,31%} \end{matrix}
Sigma neutra 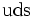\mathrm{\Sigma^0}\,\! \mathrm{uds}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.192,64 −1 0 0 7,4·10-20 \begin{matrix} {}_{\Sigma^{0}\,\rightarrow\,\Lambda^0 + \gamma} & {}_{100%} \end{matrix}
Sigma negativa 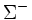\mathrm{\Sigma^-}\,\! \mathrm{dds}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.197,45 −1 0 0 1,48·10-10 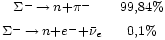\begin{matrix} {}_{\Sigma^{-}\,\rightarrow\,n + \pi^-} & {}_{99,84%} \\ {}_{\Sigma^{-}\,\rightarrow\,n + e^- + \bar{\nu}_e} & {}_{0,1%} \end{matrix}
Xi neutra 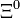\mathrm{\Xi^0}\,\! \mathrm{uss}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.314,83 −2 0 0 2,90·10-10 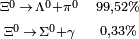\begin{matrix} {}_{\Xi^{0}\,\rightarrow\,\Lambda^0 + \pi^0} & {}_{99,52%} \\ {}_{\Xi^{0}\,\rightarrow\,\Sigma^0 + \gamma} & {}_{0,33%} \end{matrix}
Xi negativa 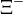\mathrm{\Xi^-}\,\! \mathrm{dss}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 1.321,31 −2 0 0 1,64·10-10 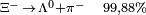\begin{matrix} {}_{\Xi^{-}\,\rightarrow\,\Lambda^0 + \pi^-} & {}_{99,88%} \end{matrix}
Omega 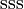\mathrm{\Omega^-}\,\! \mathrm{sss}\,\! \begin{matrix} \frac{3}{2} \end{matrix} 1.672,45 −3 0 0 8,21·10-11 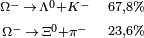\begin{matrix} {}_{\Omega^{-}\,\rightarrow\,\Lambda^0 + K^-} & {}_{67,8%} \\ {}_{\Omega^{-}\,\rightarrow\,\Xi^0 + \pi^-} & {}_{23,6%} \\ \end{matrix}
Omega encantada 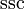\mathrm{\Omega^0_c}\,\! \mathrm{ssc}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 2.697,5 −2 +1 0 6,90·10-14 \begin{matrix} {}_{\Omega^0_c\,\rightarrow\,\Sigma^+ + K^- + K^- + \pi^+} & {}_{??\,%} \\ {}_{\Omega^0_c\,\rightarrow\,\Xi^0 + K^- + \pi^+} & {}_{??\,%} \\ \end{matrix}
Xi positiva encantada 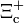\mathrm{\Xi^+_c}\,\! \mathrm{usc}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 2.468 −1 +1 0 4,42·10-13 \begin{matrix} {}_{\Xi^+_c\,\rightarrow\,\Xi^0 + \pi^+ + \pi^0} & {}_{??\,%} \\ {}_{\Xi^+_c\,\rightarrow\,\Xi^0 + e^+ + \nu_e} & {}_{??\,%} \\ \end{matrix}
Xi neutra encantada 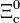\mathrm{\Xi^0_c}\,\! \mathrm{dsc}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 2.471 −1 +1 0 1,12·10-13 \begin{matrix} {}_{\Xi^0_c\,\rightarrow\,p + K^- + K^- + \pi^+} & {}_{??\,%} \\ {}_{\Xi^0_c\,\rightarrow\,\Lambda^0 + K^0_S} & {}_{??\,%} \\ \end{matrix}
Lambda encantada 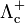\mathrm{\Lambda^+_c}\,\! \mathrm{udc}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 2.284,9 0 +1 0 2,00·10-13 \begin{matrix} {}_{\Lambda^+_c\,\rightarrow\,p + K^- + \pi^+} & {}_{??\,%} \\ {}_{\Lambda^+_c\,\rightarrow\,p + \bar{K^0} + \pi^0} & {}_{??\,%} \\ \end{matrix}
Xi doble encantada 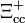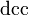\mathrm{\Xi^+_{cc}}\,\! \mathrm{dcc}\,\! \begin{matrix} ? \end{matrix} 3.519 0 +2 0 <3,30·10-14 —
Lambda inferior 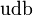\mathrm{\Lambda^0_b}\,\! \mathrm{udb}\,\! \begin{matrix} \frac{1}{2} \end{matrix} 5.624 0 0 −1 1,23·10-12 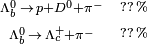\begin{matrix} {}_{\Lambda^0_b\,\rightarrow\,p + D^0 + \pi^-} & {}_{??\,%} \\ {}_{\Lambda^0_b\,\rightarrow\,\Lambda^+_c + \pi^-} & {}_{??\,%} \\ \end{matrix}
[1] El símbolo de los antibariones es el mismo pero con una barra superpuesta.
[2] Los antibariones están formados por los respectivos antiquarks.
[3] Debe ser superior a 1030 años.
[4] Vida media de los neutrones libres. En los núcleos atómicos son estables.
Se ha conseguido observar por primera vez la desintegración radiactiva del neutrón. Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutrones decaerían en todas esas partículas y además en un fotón.

Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según  la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.

Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.

Bosones

Nombre Símbolo Carga eléctrica
(e)		 Carga de color Spin Masa en reposo
(GeV/c²)		 Existencia Vida media Desintegraciones más importantes
Fotón \mathrm{\gamma}\,\! Neutra Neutra 1 Nula Confirmada Estable —
Bosón W 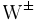\mathrm{W^{\pm}}\,\! ± 1 Neutra 1 80,425 Confirmada 3·10-25 \begin{matrix} {}_{W^{+}\,\rightarrow\,q + \bar{q}} & {}_{\approx67%} \\ {}_{W^{+}\,\rightarrow\,\ell^+ + \nu_\ell} & {}_{\approx33%} \end{matrix} [1]
Bosón Z \mathrm{Z^{0}}\,\! Neutra Neutra 1 91,187 Confirmada 3·10-25 —
Gluón \mathrm{g}\,\! Neutra Color + Anticolor 1 Nula Confirmada Estable —
Gravitón \mathrm{G}\,\! Neutra Neutra 2 Nula Hipotética Estable —
Higgs“>Bosón de Higgs \mathrm{H}\,\! Neutra Neutra 0 > 114 Hipotética Inestable \begin{matrix} {}_{H\,\rightarrow\,t + \bar{t}} & {}_{???\,%} \\ {}_{H\,\rightarrow\,b + \bar{b}} & {}_{???\,%} \end{matrix}

Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”

Foto

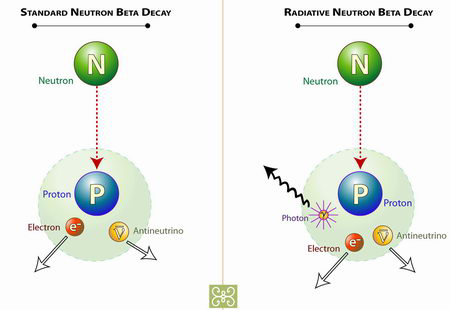
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation.  Fue difícil observar los fotones porque el haz está contaminado con fotones que fondo que producen mucho “ruido” en las medidas, por lo que era como buscar una aguja en un pajar. El decaimiento radiativo del neutrón es importante porque conecta directamente con el modelo estándar de partículas.

Si la vida de una partícula  es tan corta como 10ˉ²³ segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.

Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

            En el Universo existen muchas clases de resonancias…inesperadas

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.

Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:

∆⁺⁺→р + π⁺;  ∆⁰→р + πˉ; o п+π⁰

En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.

El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (materia), es aún limitado. Los cuadros que aparecen arriba, están referidos a las partículas más usuales como los Quarks y los Leptones (verdaderos componentes de la materia) que a su vez, son: Los Quarks los que forman a los Hadrones y los Leptones los que completan el núcleo atómico de la materia para conformar los átomos. He dejado a los mesones y a las supuestas partículas supersimétricas centrándome en las que me parecen principales en la conformación de la materia.

emilio silvera

hotmail correo[?]


Esta entrada fue publicada el domingo, 21 de septiembre de 2014 a las 8:49 y está clasificada bajo: Física Cuántica. Puede hacer un seguimiento de los comentarios de esta entrada gracias al feed RSS 2.0. Puede dejar un comentario, o enviar un trackback desde su sitio.
 


Deja un comentario



Comentario:

XHTML

Subscribe without commenting