Jun
30
¿Qué pasa con el Cambio Climático?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en EL DETERIORO DEL PLANETA tIOERRA ~
Clasificado en EL DETERIORO DEL PLANETA tIOERRA ~
 Comments (7)
Comments (7)
ENTREVISTA EN “EL MUNDO”
Richard Alley, experto en cambio climático y Premio BBVA Fronteras del Conocimiento
‘El riesgo del cambio climático para España es muy preocupante’

Richard Alley, experto en cambio climático y Premio BBVA Fronteras del Conocimiento. SERGIO ENRÍQUEZ-NISTAL
Richard Alley hace 20 años que no paga una plaza de aparcamiento. No se considera un activista ni un ejemplo de ciudadano que ha pasado a la acción, pero cada mañana acude a su puesto de catedrático de Geociencias de la Universidad de Pennsylvania en bicicleta. Alley ha pasado más de 30 años extrayendo testigos de hielo de Groenlandia o la Antártida y leyendo en ellos la historia del clima desde hace millones de años. Sus propias conclusiones le permiten hablar con la firmeza: «la huella dactilar del ser humano está en el cambio climático que estamos viviendo». Ha sido investigador principal de uno de los grupos del panel científico de Naciones Unidas para el Cambio Climático (IPCC, por sus siglas en inglés) y acaba de visitar Madrid para recoger el Premio Fundación BBVA Fronteras del Conocimientos en esa categoría.
- ¿Así que los testigos de hielo son el ADN de la Tierra?
- Sí, es fantástico. Es como leer su diario. Podemos volver atrás en el tiempo y leer lo que escribió nuestro tatarabuelo. En el día más cálido de mitad del verano en el centro de la Antártida hace -20ºC. Así que el hielo no se derrite, pero la nieve se acumula de manera diferente durante los veranos y los inviernos. Sólo con la nieve ya podemos contar los años. Pero además de nieve, también hay polvo y pequeños trozos de micrometeoritos y divertidos isótopos creados por los rayos cósmicos y hay burbujas de aire todo ello atrapado en la nieve año tras año. Así que podemos contar un relato maravilloso sobre el pasado del clima.
- ¿Hay diferencias entre el cambio climático actual y los que ha habido del pasado?
- Cuando miramos los testigos de hielo, vemos muchísimas cosas que afectan al clima. Está afectado por el Sol, por volcanes que bloquean la luz solar, por movimientos de placas geológicas que provocan cambios lentos en las corrientes marinas… Pero los cambios en la atmósfera parecen ser el factor más importante que controla el clima. Cuando la naturaleza aumenta el CO2 a través de las emisiones de los volcanes o de otros cambios, el clima se calienta. Pero también vemos que cuando el clima cambia, la vida cambia. Hay una línea y un montón de especies mueren en esa línea. Pero en el presente, hace cerca de 30 años que el Sol tiene una actividad baja, no hay volcanes que bloqueen el Sol y las órbitas del planeta no han cambiado demasiado. Hemos aumentado el CO2 y su efecto sobre el clima explica lo que ocurre. La naturaleza está cambiando y nuestra huella dactilar está en ello.
- P.- ¿Quiere decir que la vida que conocemos cambiará?
- Sí, con un muy alto grado de confianza, si cambiamos el clima, la vida también cambiará. Ya hemos visto como se están produciendo cambios en la época de floración de algunas plantas y que están ocurriendo algunas cosas raras. Pero el cambio climático que hemos causado hasta ahora está aún por debajo de 1ºC. Pero, si continuamos quemando fuentes fósiles, después de vendrán los 2ºC, y luego los 3ºC y luego los 4ºC… Podemos empezar a ver lugares que estarán más cálidos que cualquier lugar que conozcamos hoy en todo el planeta, y eso será muy duro.
- ¿Los dos grados centígrados son la última frontera o nos podemos permitir un aumento de 3ºC?
- Podemos realmente llegar a eso y mucho más si continuamos quemando fuentes fósiles. Y ésta es la media global, y debido a que la tierra se calienta mucho más que el océano, casi todos nosotros viviremos en condiciones más cálidas que esa cifra global. Pero podemos contener el calentamiento si realmente queremos hacerlo. Si somos serios en las negociaciones internacionales, podemos contener el aumento en dos grados. O, en caso contrario, nos podemos ir a tres, cuatro o más, sabiendo que cada uno de esos grados será más costoso y más peligroso que el anterior.
- ¿Confía en que en París se llegue a un acuerdo que logre controlar el aumento de temperatura en dos grados?
- No confío, ya veremos. Es posible. Estamos en un momento muy interesante, con la encíclica del Papa…
- ¿Son buenas señales?
- Sí, muy buenas. Es muy interesante el texto del Papa. La ciencia en la que se basa es muy sólida.
- ¿Qué quiere decir para España un aumento como el que estamos contemplando?
- Es muy preocupante. Acabamos de ver los efectos de las olas de calor en India y Paquistán. Las zonas secas alrededor de los trópicos se harán mayores y esto puede influir en España. Si continuamos por el mismo camino, en la mayoría de lugares de la Tierra el peor verano que se recuerda hoy en día estará por debajo de la media a finales de siglo.
- Abandonando los mensajes catastróficos, ¿qué podemos hacer como ciudadanos?
- Tenemos una larguísima tradición de quemar cosas para conseguir energía mucho más rápido de lo que la naturaleza crea otras nuevas. Quemábamos la grasa de las ballenas para tener luz por las noches y casi nos quedamos sin ballenas. Y se ha recuperado la población porque encontramos otra cosa que quemar: combustibles fósiles. Tenemos que crear un sistema energético sostenible que podamos permitirnos y que podamos construir. Dentro de 30 años tendremos un sistema que podrá abastecernos a todos prácticamente para siempre. Podremos dejar de preocuparnos por lo que vendrá después. Podremos abastecer a nuestros nietos y a los nietos de nuestros nietos.
Jun
26
En Física hablamos de masa, inercia…, ¡de tántas cosas! Pero, ¿son...
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Cuando hablamos de masa, nos estamos refiriendo a la medida de la inercia de un cuerpo, es decir, su resistencia a la aceleración. Todos sabemos la inmensa cantidad de combustible que se necesita para enviar al espacio exterior a esos transbordadores que llevan suministros y astronáutas al espacio exterior para el mantenimeinto de la Estación Espacial Internacional. El esfuerzo, es vencer la masa que se quiere transportar hasta que esta, alcanzando los 11 km/s de velocidad, pueda escapar de la fuerza de gravedad de la Tierra y poder así, cumplir con su cometido.

De acuerdo con las leyes de Newton del movimiento, si dos masas distintas, m1 y m2, son hechas colisionar en ausencia de cualquier otra fuerza, ambas experimentaran la misma fuerza de colisión. Si los dos cuerpos adquieren aceleraciones a1 y a2, como resultado de la colisión, entonces m1 a1 = m2 a2. Esta ecuación permite comparar dos masas. Si una de las masas se considera como una masa estándar, la masa de todas las demás puede ser medida comparándola con esta masa estándar. El cuerpo utilizado para este fin es un cilíndro de un kilógramo de una aleación de platino iridio. llamado el estándar internacional de masa. La masa definida de esta forma es llamada masa inercial del cuerpo.

Las masas también se pueden definir midiendo la fuerza gravitacional que producen. Por tanto, de acuerdo con la ley de gravitación de Newton, mg = Fd2 / MG, donde M es la masa de un cuerpo estándar situado a una distancia d del cuerpo de masa mg; F es la fuerza gravitacional entre ellos, y G es la constante gravitacional. La masa definida de esta forma es la masa gravitacional. En el siglo XIX, Roland Eötvös (1848-1919) demostró experimentalmente que las masas inerciales y gravitatorias son indistinguibles, es decir, m1 = mg.
Aunque la masa se define formalmente utilizando el concepto de inercia, es medida habitualmente por gravitación. El peso (W) de un cuerpo es la fuerza con la que un cuerpo es atraído gravitacionalmente a la Tierra, corregido por el efecto de la rotación, y es igual al producto de la masa del cuerpo y la aceleración en caída libre (g), es decir, W = mg.

Kilogramo patrón.
El kilogramo (unidad de masa) tiene su patrón en: la masa de un cilindro fabricado en 1880, compuesto de una aleación de platino-iridio (90 % platino – 10 % iridio), creado y guardado en unas condiciones exactas, y que se guarda en la Oficina Internacional de Pesos y Medidas en Sevres, cerca de París.
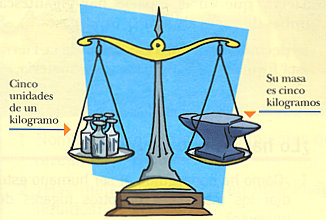 |
| Una balaza mide solo cantidad de masa. |
La masa es la única unidad que tiene este patrón, además de estar en Sevres, hay copias en otros países que cada cierto tiempo se reúnen para ser regladas y ver si han perdido masa con respecto a la original.
No olvidemos que medir es comparar algo con un patrón definido universalmente.
¿Y el peso?
De nuevo, atención a lo siguiente: la masa (la cantidad de materia) de cada cuerpo es atraída por la fuerza de gravedad de la Tierra. Esa fuerza de atracción hace que el cuerpo (la masa) tenga un peso, que se cuantifica con una unidad diferente: el Newton (N).
La UNIDAD DE MEDIDA DEL PESO ES EL NEWTON (N)
Entonces, el peso es la fuerza que ejerce la gravedad sobre una masa y ambas magnitudes son proporcionales entre sí, pero no iguales, pues están vinculadas por el factor aceleración de la gravedad.
En el lenguaje común, el peso y la masa son frecuentemente usados como sinónimos; sin embargo, para fines científicos son muy diferentes. La masa es medida en kilogramos; el peso, siendo una fuerza, es medido en newtons (símbolo N. Unidad del SI de la fuerza, siendo la fuerza requerida para comunicar a una masa de un kilogramo una aceleración de 1 m s –2). Es más, el peso depende de donde sea medido, porque el valor de g es distintos en diferentes puntos de la superficie de la Tierra. La masa, por el contrario, es constante donde quiera que se mida, sujeta a la teoría especial de la relatividad. De acuerdo con esta teoría, publicada por Albert Einstein en 1905, la masa de un cuerpo es una medida de su contenido total de energía.




Por tanto, si la energía del cuerpo crece, por ejemplo, por un aumento de su energía cinética o temperatura, entonces su masa también crece. De acuerdo con esta ley, un aumento de energía ΔE está acompañado de un aumento de masa Δm, en conformidad con la ecuación de masa-energía Δm = ΔE/c2, donde c es la velocidad de la luz. Por tanto, si un kilo de agua se eleva de temperatura en 100 K, su energía interna aumentará en 4 x 10 –12 kg. Este es, por supuesto, un incremento despreciable y la ecuación de masa-energía es sólo significativa para energías extremadamente altas. Por ejemplo, la masa de un electrón es siete veces mayor si se mueve con relación a un observador al 99% de la velocidad de la luz.
Ya sabemos que, se ha comprobado una y mil veces que, la teoría de Einstein de la relatividad especial es cierta en el sentido de que, al ser la velocidad de la luz el límite de velocidad del Universo, nada puede ir más rápido que la luz, cuando un cuerpo viaja a velocidades cercanas a la de la luz, a medida que se acerca a ella, puede ver como su masa aumenta, ya que, la energía de movimiento se convierte en masa al no poder conseguir su objetivo de marchar más rápido que la luz.

En los anillos enterrados en las entrañas de la Tierra, haces de partículas son lanzadas a la velocidad de la luz para que colisionen y, su peso aumenta conforme se van acercando a ese límite marcado por el universo.
La masa relativista de un cuerpo medida por un observador (un físico del LHC que mide el aumento de masa de los protones a medida que adquieren velocidad en el acelerador de partículas del CERN) con respecto al cual este cuerpo se mueve. De acuerdo con la teoría de Einstein, la masa m de un cuerpo moviendose a velocidad v está dada por m = m0/√ (1 – v2 / c2), donde m0 es su masa en reposo y c es la velocidad de la luz. La masa relativista solo difiere significativamente de la masa en reposo si su velocidad es una fracción apreciable de la velocidad de la luz. Si v = c/2, por ejemplo, la masa relativista es un 15% mayor que la masa en reposo.
Según las consecuencias obtenidas en el proyecto Manhattan, lo que sí es seguro es que, una pequeña fracción de materia, contiene una gran cantidad de energía. Según nos decía Asimov: “…un sólo gramo de materia se podría convertir en energía eléctrica que bastaría para mantener luciendo continuamente una bombilla de 100 vatios durante unos 28.200 años. O bien, la energía que representa un sólo gramo de materia es equivalente a la que se obtendría de quemar unos 32 millones de litros de gasolina”.

Una cosa si que nos puede quedar muy clara: Aunque sabemos algunas cosas sobre la masa y lo que entendemos por la energía, no podemos decir que, al día de hoy, “sepamos de verdad”, lo que la masa y la energía son.
Seguiremos aprendiendo. Sin embargo, nunca dejes de tener en cuenta que, lo que es cierto hoy, mañana será una verdad distinta. Todo dependen de la teoría aceptada en el momento, toda vez que, con el paso del tiempo las ideas evolucionan y todo es mejorables a medida que nuestros conocimientos avanzan. Así que la idea que podamos tener de Gravedad, masa, energía e inercia, mañana podría ser distinta a la que hoy podamos tener.
emilio silvera
Jun
26
Los grandes números distintivos del Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las constantes de la Naturaleza ~
Clasificado en Las constantes de la Naturaleza ~
 Comments (4)
Comments (4)
Si alguna de estas constantes de la Naturaleza, variaran tan sólo una millonésima, la vida no estaría presente
“En la Física existen una serie de magnitudes que contienen información que es independiente del sistema de medida que elijamos, lo cual es muy valioso no sólo en los cálculos. Además, estos parámetros que fija la naturaleza aparecen en las ecuaciones como parámetros que debemos ajustar lo más que podamos para que nuestras predicciones y nuestros modelos se ajusten a la realidad en la medida de lo posible.
Y aquí es donde viene el problema. Que son parámetros, es decir, su valor cuantitativo no es deducible de la teoría y por tanto hay que medirlo. Y esto añade la dificultad no sólo de idear un experimento, sino de hacerlo lo bastante preciso como para que el modelo sirva para algo.
El Modelo Estándar por ejemplo, que es el paradigma actual en el que se mueve la física de partículas y que recoge las interacciones fundamentales tiene unos 25 parámetros que se deben ajustar. Parámetros tales como la carga eléctrica, la masa, el espín, las constantes de acoplamiento de los campos, que miden la intensidad que éstos tienen, etcétera.
Ya no sólo se trata de averiguar el valor de cada una de ellas. Tampoco sabemos decir de antemano cuantas constantes fundamentales puede haber. Y es evidente que cuantas más constantes hay, más complicado se nos hace nuestro modelo.”
Si miramos hacia atrás en el Tiempo podemos contemplar los avances que la Humanidad logró en los últimos tiempos, caigo en la cuenta de que poco a poco hemos sido capaces de identificar una colección de números mágicos y misteriosos arraigados en la regularidad de la experiencia.
¡Las constantes de la naturaleza!
Dan al universo su carácter distintivo y lo hace singular, distinto a otros que podría nuestra imaginación inventar. Estos números misteriosos, a la vez que dejan al descubierto nuestros conocimientos, también dejan al desnudo nuestra enorme ignorancia sobre el universo que nos acoge. Las medimos con una precisión cada vez mayor y modelamos nuestros patrones fundamentales de masa y tiempo alrededor de su invarianza; no podemos explicar sus valores.

Nunca nadie ha explicado el valor numérico de ninguna de las constantes de la naturaleza. ¿Recordáis el 137? Ese número puro, adimensional, que guarda los secretos del electrón (e), de la luz (c) y del cuanto de acción (h). Hemos descubierto otros nuevos, hemos relacionado los viejos y hemos entendido su papel crucial para hacer que las cosas sean como son, pero la razón de sus valores sigue siendo un secreto profundamente escondido.
Buscar esos secretos ocultos implica que necesitamos desentrañar la teoría más profunda de todas y la más fundamental de las leyes de la naturaleza: descubrir si las constantes de la naturaleza que las definen están determinadas y conformadas por alguna consistencia lógica superior o si, por el contrario, sigue existiendo un papel para el azar.

Si estudiamos atentamente las constantes de la naturaleza nos encontramos con una situación muy peculiar. Mientras parece que ciertas constantes estuvieran fijadas, otras tienen espacio para ser distintas de las que son, y algunas no parecen afectadas por ninguna otra cosa del - o en el – universo.
¿Llegaron estos valores al azar?
¿Podrían ser realmente distintos?

¿Cuán diferentes podrían ser para seguir albergando la existencia de seres vivos en el universo?
En 1.986, el libro The Anthropic Cosmological Principle exploraba las diez maneras conocidas en que la vida en el universo era sensible a los valores de las constantes universales. Universos con constantes ligeramente alteradas nacerían muertos, privados del potencial para desarrollar y sostener la complejidad que llamamos vida.
En la literatura científica puede encontrarse todo tipo de coincidencias numéricas que involucran a los valores de las constantes de la naturaleza. He aquí algunas de las fórmulas propuestas (ninguna tomada en serio) para la constante de estructura fina.
Valor experimental: 1/α = 137’035989561…
- Lewis y Adams: 1/α = 8π (8π5 / 15)1/3 = 137’384
- Eddington: 1/α = (162 – 16) / 2 + 16 – 1 = 137
- Wiler: 1/α = (8π4 / 9)(245! / π5)1/4 = 137’036082
- Aspden y Eagles: 1/α = 108π (8 / 1.843)1/6 = 137’035915

Por supuesto, si la teoría M da al fin con una determinación del valor de 1/α podría parecerse perfectamente a una de estas fórmulas especulativas. Sin embargo ofrecería un amplio y constante edificio teórico del que seguiría la predicción.
También tendría que haber, o mejor, que hacer, algunas predicciones de cosas que todavía no hemos medido; por ejemplo, las siguientes cifras decimales de 1/α, que los futuros experimentadores podrían buscar y comprobar con medios más adelantados que los que ahora tenemos, a todas luces insuficientes en tecnología y potencia.
Todos estos ejercicios de juegos mentales numéricos se acercan de manera impresionante al valor obtenido experimentalmente, pero el premio para el ingeniero persistente le corresponde a Gary Adamson, cuya muestra de 137-logía se mostraron en numerosas publicaciones.
Estos ejemplos tienen al menos la virtud de surgir de algún intento de formular una teoría de electromagnetismo y partículas. Pero hay también matemáticos “puros” que buscan cualquier combinación de potencias de números pequeños y constantes matemáticas importantes, como π, que se aproxime al requerido 137’035989561… He aquí algún ejemplo de este tipo.
- Robertson: 1/α = 2-19/4 310/3 517/4 π-2 = 137’03594
- Burger: 1/α = (1372 + π2)1/2 = 137’0360157

Unidades naturales que no inventó el hombre
Ni siquiera el gran físico teórico Werner Heisenberg pudo resistirse a la ironía o irónica sospecha de que…
“En cuanto al valor numérico, supongo que 1/α = 24 33 / π, pero por supuesto es una broma.”
Arthur Eddington, uno de los más grandes astrofísicos del siglo XX y una notable combinación de lo profundo y lo fantástico, más que cualquier figura moderna, fue el responsable impulsor de poner en marcha los inacabables intentos de explicar las constantes de la naturaleza mediante auténticas proezas de numerología pura. Él también advirtió un aspecto nuevo y especular de las constantes de la naturaleza.
“He tenido una visión muy extraña, he tenido un sueño; supera el ingenio del hombre decir qué sueño era. El hombre no es más que un asno cuando tiene que exponer este sueño. Se llamará el sueño del fondo, porque no tiene fondo.”
A. S. Eddington
“El conservadurismo recela del pensamiento, porque el pensamiento en general lleva a conclusiones erróneas, a menos que uno piense muy, muy intensamente.”
Roger Scruton

Todo lo que existe… ¡Tiene una explicación!
Hay que prestar atención a las coincidencias. Uno de los aspectos más sorprendentes en el estudio del universo astronómico durante el siglo XX, ha sido el papel desempeñado por la coincidencia: que existiera, que fuera despreciada y que fuera recogida. Cuando los físicos empezaron a apreciar el papel de las constantes en el dominio cuántico y a explorar y explorar la nueva teoría de la gravedad de Einstein para describir el universo en conjunto, las circunstancias eran las adecuadas para que alguien tratara de unirlas.
Entró en escena Arthur Eddington; un extraordinario científico que había sido el primero en descubrir cómo se alimentaban las estrellas a partir de reacciones nucleares. También hizo importantes contribuciones a nuestra comprensión de la galaxia, escribió la primera exposición sistemática de la teoría de la relatividad general de Einstein y fue el responsable de verificar, en una prueba decisiva durante un eclipse de Sol, la veracidad de la teoría de Einstein en cuanto a que el campo gravitatorio del Sol debería desviar la luz estelar que venía hacia la Tierra en aproximadamente 1’75 segmentos de arco cuando pasaba cerca de la superficie solar, y así resultó.
“Arthur Eddington creyó en las teorías de Einstein desde el principio, y fueron sus datos tomados durante el eclipse solar de 1919 los que dieron la prueba experimental de la teoría general de la relatividad. La amplia cobertura informativa de los resultados de Eddington llevó a la teoría de la relatividad, y al propio Einstein, a unos niveles de fama sin precedentes.
Arthur Eddington está considerado uno de los más importantes astrónomos ingleses del siglo XX. Se especializó en la interpretación de las observaciones de los movimientos de las estrellas en el Observatorio de Greenwich. En 1913, fue uno de los primeros científicos no alemanes en entrar en contacto con las primeras versiones de la teoría general de la relatividad, e inmediatamente se convirtió en un declarado partidario.”
( http://www.experientiadocet.com)
Albert Einstein y Arthur Stanley Eddington se conocieron y se hicieron amigos. Se conservan fotos de los dos juntos conversando sentados en un banco en el jardín de Eddington en el año 1.930, donde fueron fotografiados por la hermana del dueño de la casa.
Aunque Eddington era un hombre tímido con pocas dotes para hablar en público, sabía escribir de forma muy bella, y sus metáforas y analogías aún las utilizan los astrónomos que buscan explicaciones gráficas a ideas complicadas. Nunca se casó y vivió en el observatorio de Cambridge, donde su hermana cuidaba de él y de su anciana madre.
Eddington creía que a partir del pensamiento puro sería posible deducir leyes y constantes de la naturaleza y predecir la existencia en el universo de cosas como estrellas y galaxias. ¡Se está saliendo con la suya!
Entre los números de Eddington, uno lo consideró importante y lo denominó “número de Eddington”, que es igual al número de protones del universo visible. Eddington calculó (a mano) este número enorme y de enorme precisión en un crucero trasatlántico concluyendo con esta memorable afirmación.
“Creo que en el universo hay
15.747.724.136.275.002.577.605.653.961.181.555.468.044.717.914.527.116.709.366.231.425.076.185.631.031.296
protones y el mismo número de electrones.”
Este número enorme, normalmente escrito NEdd, es aproximadamente igual a 1080. Lo que atrajo la atención de Eddington hacia él era el hecho de que debe ser un número entero, y por eso en principio puede ser calculado exactamente.
Durante la década de 1.920, cuando Eddington empezó su búsqueda para explicar las constantes de la naturaleza, no se conocían bien las fuerzas débil y fuerte, y las únicas constantes dimensionales de la física que sí se conocían e interpretaban con confianza eran las que definían la gravedad y las fuerzas electromagnéticas.

No siempre sabemos valorar la grandeza a la que puede llegar la mente humana: “… puedan haber accedido a ese mundo mágico de la Naturaleza para saber ver primero y desentrañar después, esos números puros y adimensionales …”
Eddington las dispuso en tres grupos o tres puros números adimensionales. Utilizando los valores experimentales de la época, tomó la razón entre las masas del protón y del electrón:
mp / me ≈ 1.840
La inversa de la constante de estructura fina:
2πhc / e2 ≈ 137
Y la razón entre la fuerza gravitatoria y la fuerza electromagnética entre un electrón y un protón:
e2 / Gmpme ≈ 1040
A éstas unió o añadió su número cosmológico, NEdd ≈ 1080.

¿No cabría la posibilidad de que todos los grandes sucesos presentes correspondan a propiedades de este Gran Número [1040] y, generalizando aún más, que la historia entera del universo corresponda a propiedades de la serie entera de los números naturales…? Hay así una posibilidad de que el viejo sueño de los filósofos de conectar la naturaleza con las propiedades de los números enteros se realice algún día.
Eddington a estos cuatro números los llamó “las constantes últimas”, y la explicación de sus valores era el mayor desafío de la ciencia teórica.
“¿Son estas cuatro constantes irreducibles, o una unificación posterior de la física demostrará que alguna o todas ellas pueden ser prescindibles?
¿Podrían haber sido diferentes de los que realmente son?”
De momento, con certeza nadie ha podido contestar a estas dos preguntas que, como tantas otras, están a la espera de esa Gran Teoría Unificada del Todo, que por fin nos brinde las respuestas tan esperadas y buscadas por todos los grandes físicos del mundo. ¡Es todo tan complejo! ¿Acaso es sencillo y no sabemos verlo? Seguramente un poco de ambas cosas; no será tan complejo, pero nuestras mentes aún no están preparadas para ver su simple belleza. Una cosa es segura, la verdad está ahí, esperándonos.
Para poder ver con claridad no necesitamos gafas, sino evolución. Hace falta alguien que, como Einstein hace 100 años, venga con nuevas ideas y revolucione el mundo de la física que, a comienzos del siglo XXI, está necesitada de un nuevo y gran impulso. ¿Quién será el elegido? Por mi parte me da igual quién pueda ser, pero que venga pronto. Quiero ser testigo de los grandes acontecimientos que se avecinan, la teoría de supercuerdas y mucho más.
emilio silvera
Jun
25
El fascinante “universo” de las partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
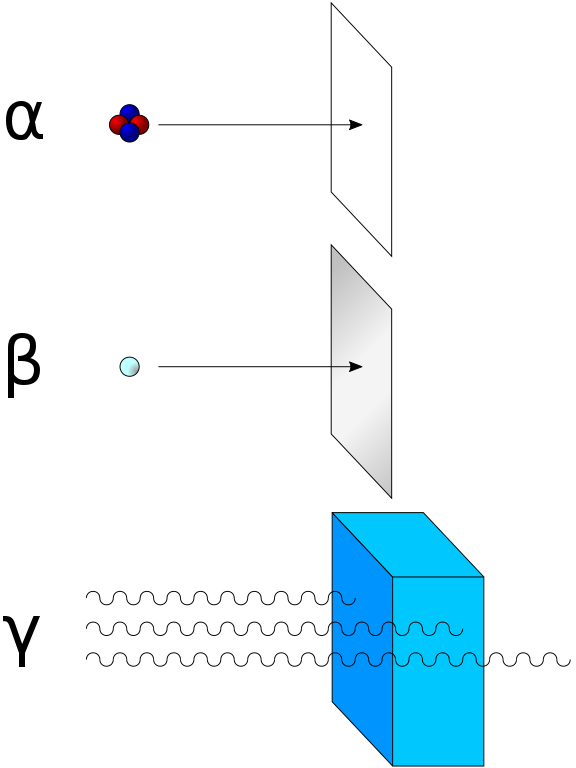
La radiación alfa consiste en núcleos de helio-4 (4He) y es detenida fácilmente por una hoja de papel. La radiación Beta que consiste en electrones, es detenida por una placa de aluminio. La radiación gamma es finalmente absorbida cuando penetra en un material denso. El plomo es bueno en la absorción de la radiación gamma, debido a su densidad.
¿Qué no será capaz de inventar el hombre para descubrir los misterios de la naturaleza?
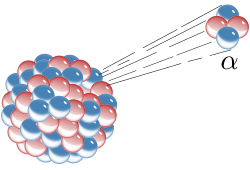
Ha pasado mucho tiempo desde que Rutherford identificara la primera partícula nuclear (la partícula alfa). El camino ha sido largo y muy duro, con muchos intentos fallidos antes de ir consiguiendo los triunfos (los únicos que suenan), y muchos han sido los nombres que contribuyen para conseguir llegar al conocimiento del átomo y del núcleo actual; los electrones circulando alrededor del núcleo, en sus diferentes niveles, con un núcleo compuesto de protones y neutrones que, a su vez, son constituidos por los quarks allí confinados por los gluones, las partículas mediadoras de la fuerza nuclear fuerte. Pero, ¿qué habrá más allá de los quarks?, ¿las supercuerdas vibrantes? Algún día se sabrá.
Partículas
El universo de las partículas es fascinante. Cuando las partículas primarias chocan con átomos y moléculas en el aire, aplastan sus núcleos y producen toda clase de partículas secundarias. En esta radiación secundaria (aún muy energética) la que detectamos cerca de la Tierra, por los globos enviados a la atmósfera superior, han registrado la radiación primaria.

El físico estadounidense Robert Andrews Millikan, que recogió una gran cantidad de información acerca de esta radiación (y que le dio el nombre de rayos cósmicos), decidió que debería haber una clase de radiación electromagnética. Su poder de penetración era tal que, parte del mismo, atravesaba muchos centímetros de plomo. Para Millikan, esto sugería que la radiación se parecía a la de los penetrantes rayos gamma, pero con una longitud de onda más corta.
Otros, sobre todo el físico norteamericano Holly Compton, no estaban de acuerdo en que los rayos cósmicos fuesen partículas. Había un medio para investigar este asunto; si se trataba de partículas cargadas, deberían ser rechazadas por el campo magnético de la Tierra al aproximarse a nuestro planeta desde el espacio exterior. Compton estudió las mediciones de la radiación cósmica en varias latitudes y descubrió que en realidad se curvaban con el campo magnético: era más débil cera del ecuador magnético y más fuerte cerca de los polos, donde las líneas de fuerza magnética se hundían más en la Tierra.
Las partículas cósmicas primarias, cuando entran en nuestra atmósfera, llevan consigo unas energías fantásticas, muy elevadas. En general, cuanto más pesado es el núcleo, más raro resulta entre las partículas cósmicas. Núcleos tan complejos como los que forman los átomos de hierro se detectaron con rapidez; en 1.968, otros núcleos como el del uranio. Los núcleos de uranio constituyen sólo una partícula entre 10 millones. También se incluirán aquí electrones de muy elevada energía.
Ahora bien, la siguiente partícula inédita (después del neutrón) se descubrió en los rayos cósmicos. A decir verdad, cierto físico teórico había predicho ya este descubrimiento. Paul Adrien Dirac había aducido, fundándose en un análisis matemático de las propiedades inherentes a las partículas subatómicas, que cada partícula debería tener su antipartícula (los científicos desean no sólo que la naturaleza sea simple, sino también simétrica). Así pues, debería haber un antielectrón, salvo por su carga que sería positiva y no negativa, idéntico al electrón; y un antiprotón, con carga negativa en vez de positiva.
En 1.930, cuando Dirac expuso su teoría, no llamó demasiado la atención en el mundo de la ciencia. Pero, fiel a la cita, dos años después apareció el antielectrón. Por entonces, el físico americano Carl David Anderson trabajaba con Millikan en un intento por averiguar si los rayos cósmicos eran radiación electromagnética o partículas. Por aquellas fechas, casi todo el mundo estaba dispuesto a aceptar las pruebas presentadas por Compton, según las cuales, se trataría de partículas cargadas; pero Millikan no acababa de darse por satisfecho con tal solución.

La existencia de los pòsitrones puede llegar a ser indefinida, lo que ocurre es que, al estar en un universo repleto de electrones, cuando apenas han iniciado su veloz carrera se encuentran con uno y, su carrera, dura apenas una millonésima de segundo y, el electrón y el positrón quedan asociados y giran alrededor de un centro de fuerza común

Anderson se propuso averiguar si los rayos cósmicos que penetraban en una cámara de ionización se curvaban bajo la acción de un potente campo magnético. Al objeto de frenar dichos rayos lo suficiente como para detectar la curvatura, si la había, puso en la cámara una barrera de plomo de 6’35 mm de espesor. Descubrió que, cuando cruzaba el plomo, la radiación cósmica trazaba una estela curva a través de la cámara; y descubrió algo más. A su paso por el plomo, los rayos cósmicos energéticos arrancaban partículas de los átomos de plomo. Una de esas partículas dejó una estela similar a la del electrón. ¡Allí estaba, pues, el antielectrón de Dirac! Anderson le dio el nombre de positrón. Tenemos aquí un ejemplo de radiación secundaria producida por rayos cósmicos. Pero aún había más, pues en 1.963 se descubrió que los positrones figuraban también entre las radiaciones primarias.
Abandonado a sus propios medios, el positrón es tan estable como el electrón (¿y por qué no habría de serlo si el idéntico al electrón, excepto en su carga eléctrica?). Además, su existencia puede ser indefinida. Ahora bien, en realidad no queda abandonado nunca a sus propios medios, ya que se mueve en un universo repleto de electrones. Apenas inicia su veloz carrera (cuya duración ronda la millonésima de segundo), se encuentra ya con uno.
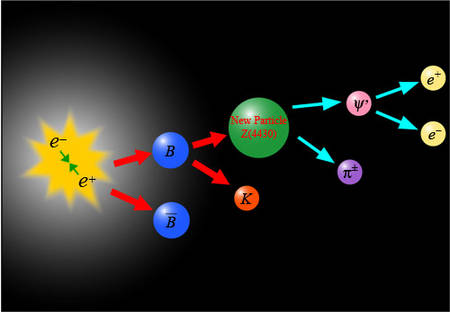
Así, durante un momento relampagueante quedaron asociados el electrón y el positrón; ambas partículas girarán en torno a un centro de fuerza común. En 1.945, el físico americano Arthur Edwed Ruark sugirió que se diera el nombre de positronio a este sistema de dos partículas, y en 1.951, el físico americano de origen austriaco Martin Deutsch consiguió detectarlo guiándose por los rayos gamma característicos del conjunto.
Pero no nos confundamos, aunque se forme un sistema positronio, su existencia durará, como máximo, una diezmillonésima de segundo. El encuentro del electrón-positrón provoca un aniquilamiento mutuo; sólo queda energía en forma de radiación gamma. Ocurre pues, tal como había sugerido Einstein: la materia puede convertirse en energía y viceversa. Por cierto, que Anderson consiguió detectar muy pronto el fenómeno inverso: desaparición súbita de rayos gamma para dar origen a una pareja electrón-positrón. Este fenómeno se llama producción en pareja. Anderson compartió con Hess el premio Nobel de Física de 1.936.
Poco después, los Joliot-Curie detectaron el positrón por otros medios, y al hacerlo así realizaron, de paso, un importante descubrimiento. Al bombardear los átomos de aluminio con partículas alfa, descubrieron que con tal sistema no sólo se obtenían protones, sino también positrones. Cuando suspendieron el bombardeo, el aluminio siguió emitiendo positrones, emisión que sólo con el tiempo se debilitó. Aparentemente habían creado, sin proponérselo, una nueva sustancia radiactiva. He aquí la interpretación de lo ocurrido según los Joliot-Curie: cuando un núcleo de aluminio absorbe una partícula alfa, la adición de los dos protones transforma el aluminio (número atómico 13) en fósforo (número atómico 15). Puesto que las partículas alfa contienen cuatro nucleones en total, el número masivo se eleva 4 unidades, es decir, del aluminio 27 al fósforo 31. Ahora bien, si al reaccionar se expulsa un protón de ese núcleo, la reducción en una unidad de sus números atómicos y masivos hará surgir otro elemento, o sea, el silicio 30.
Puesto que la partícula alfa es el núcleo del helio, y un protón es el núcleo del hidrógeno, podemos escribir la siguiente ecuación de esta reacción nuclear:
aluminio 27 + helio 4 = silicio 30 + hidrógeno 1
Nótese que los números másicos se equilibran:
27 + 4 = 30 + 1
Adentrarse en el universo de las partículas que componen los elementos de la tabla periódica, y en definitiva, la materia conocida, es verdaderamente fantástico.
Tan pronto como los Joliot-Curie crearon el primer isótopo radiactivo artificial, los físicos se lanzaron en tropel a producir tribus enteras de ellas. En realidad, las variedades radiactivas de cada elemento en la tabla periódica son producto de laboratorio. En la moderna tabla periódica, cada elemento es una familia con miembros estables e inestables, algunos procedentes de la naturaleza, otros sólo del laboratorio. Por ejemplo, el hidrógeno presenta tres variedades: en primer lugar, el corriente, que tienen un solo protón. En 1.932, el químico Harold Urey logró aislar el segundo. Lo consiguió sometiendo a lenta evaporación una gran cantidad de agua, de acuerdo con la teoría de que los residuos representarían una concentración de la forma más pesada del hidrógeno que se conocía, y, en efecto, cuando se examinaron al espectroscopio las últimas gotas de agua no evaporadas, se descubrió en el espectro una leve línea cuya posición matemática revelaba la presencia de hidrógeno pesado.
El núcleo de hidrógeno pesado está constituido por un protón y un neutrón. Como tiene un número másico de 2, el isótopo es hidrógeno. Urey llamó a este átomo deuterio (de la voz griega deutoros, “segundo”), y el núcleo deuterón. Una molécula de agua que contenga deuterio se denomina agua pesada, que tiene puntos de ebullición y congelación superiores al agua ordinaria, ya que la masa del deuterio es dos veces mayor que la del hidrógeno corriente. Mientras que ésta hierve a 100º C y se congela a 0º C, el agua pesada hierve a 101’42º C y se congela a 3’79º C. El punto de ebullición del deuterio es de -23’7º K, frente a los 20’4º K del hidrógeno corriente. El deuterio se presenta en la naturaleza en la proporción de una parte por cada 6.000 partes de hidrógeno corriente. En 1.934 se otorgó a Urey el premio Nobel de Química por su descubrimiento del deuterio.

El deuterio resultó ser una partícula muy valiosa para bombardear los núcleos. En 1.934, el físico australiano Marcus Lawrence Edwin Oliphant y el austriaco P. Harteck atacaron el deuterio con deuterones y produjeron una tercera forma de hidrógeno, constituido por un protón y dos neutrones. La reacción se planteó así:
hidrógeno 2 + hidrógeno 2 = hidrógeno 3 + hidrógeno 1
Este nuevo hidrógeno superpesado se denominó tritio (del griego tritos, “tercero”); su ebullición a 25º K y su fusión a 20’5º K.
Como es mi costumbre, me desvío del tema y sin poderlo evitar, mis ideas (que parecen tener vida propia), cogen los caminos más diversos. Basta con un fugaz recuerdo; lo sigo y me lleva a destinos distintos de los que me propuse al comenzar. Así, en este caso, me pasé a la química, que también me gusta mucho y está directamente relacionada con la física; de hecho son hermanas: la madre, las matemáticas, la única que finalmente lo podrá explicar todo.
emilio silvera
Jun
24
Conocer mejor el planeta Tierra
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Tierra y su energía ~
Clasificado en La Tierra y su energía ~
 Comments (1)
Comments (1)

Esta es nuestra casa y, debemos procurar mantenerla limpia (no por si viene una visita, que espero que no sea pronto), sino que, es vital para nosotros y para la vida en general. No siempre somos conscientes del daño que muchas de nuestras actividades pueden hacer al planeta que nos cobija. Pero veámos algunos detalles que definen a este planeta único en nuestro entorno espacial.
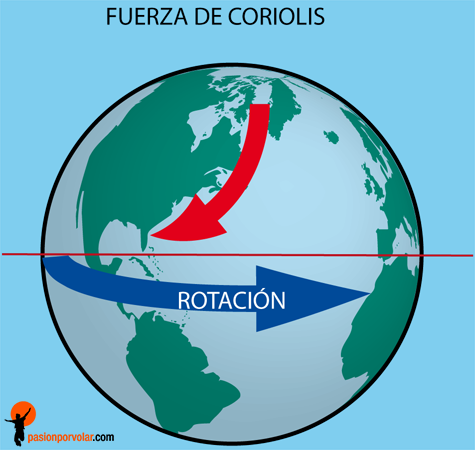
Las fuerzas que actúan sobre la Tierra, como planeta en el espacio, tiene profundas implicaciones energéticas. La gravitación ordena y orienta, y obstaculiza y facilita los flujos de energía cinética. La rotación genera la fuerza centrífuga y la de Coriolis: la primera achata el planeta por los polos ensanchándolo por el ecuador, y la segunda desvía los vientos y las corrientes de los océanos (a la derecha del hemisferio norte y a la izquierda en el hemisferio sur). La rotación es también la causa de los ritmos diarios de las plantas y animales, y de la desaceleración de la Tierra, que alarga el día un promedio de 1’5 ms cada siglo, lo que representa una pérdida de tres teravatios por fricción de mareas.

Pero ni la gravitación ni la rotación (fricción) hacen de la Tierra un planeta único entre los cuerpos celestes de nuestro entorno. Su exclusividad procede de sus propiedades térmicas internas, que causan los ciclos geotectónicos que modifican la superficie, y de su atmósfera, océanos y plantas que transforman la radiación solar que reciben. Los orígenes de estos procesos no están claros.
Podemos fijar la edad de la Tierra en algo más de los 4.000 millones de años por la desintegración de los isótopos radiactivos, pero poco podemos asegurar sobre la formación del planeta o sobre la energética de la Tierra primitiva. Sobre el tema circulan varias teorías, y es muy plausible que el origen del Sistema Solar planetario fuera una nube interestelar densa en la que el Sol se formó por una inestabilidad gravitatoria y que la posterior aglomeración del resto de esta materia dispersa, que giraba a distintas distancias, a su alrededor, diera lugar a los planetas. No está claro si al principio la Tierra estaba extremadamente caliente o relativamente fría. Me inclino por lo primero y estimo que el enfriamiento fue gradual con los cambios de atmósferas y la creación de los océanos.

Esta de arriba podría ser una imagen cotidiana en la Tierra primitiva

Las incertidumbres geológicas básicas se extienden hasta el presente. Diferentes respuestas a cuestiones como la cantidad de 40K en el núcleo terrestre o sobre la convección del magma en el manto (hay una o dos celdas) dan lugar a diferentes explicaciones para el flujo de calor y la geotectónica de la Tierra. Lo que sí está claro es que el flujo interno de calor, menos de 100 mW/m2, tiene un efecto pequeño comparado con la reflexión, absorción y emisión de la radiación solar.
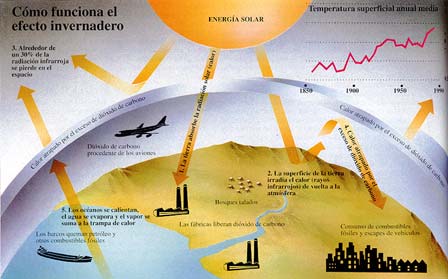
El balance de la radiación terrestre (Rp) en la capa alta de la atmósfera es la suma de la radiancia extraterrestre (la constante sola Q0) reducida por el albedo planetario y el flujo saliente de larga longitud de onda (Qi): Rp = Q0(1-ap) + Qi = 0. El flujo emitido es igual a la suma de la radiación atmosférica y la terrestre: Qi = Qea + Qes. Los balances de la radiación en la atmósfera (Ra) y en la superficie de la Tierra (Rs) son iguales, respectivamente, a la diferencia entre la correspondiente absorción y emisión: Ra = Qaa + Qea y Rs = Qas + Qes, de manera que Rp = Ra + Rs = 0. Hay que continuar explicando la radiación saliente con los flujos irradiados y emitidos por la superficie terrestre, el flujo de radiación medio absorbida, etc., etc., etc., con una ingente reseña de símbolos y tedioso esquemas que, a mi parecer, no son legibles para el lector normal y no versado en estos conocimientos. Así que, aunque sea mutilar el trabajo, desisto de continuar por ese camino y prosigo por senderos más amenos y sugestivos para el lector.

El impacto de la radiación solar en la atmósfera terrestre, en una gran tormenta solar de 2003. (Crédito: NASA / Goddard
La fuente más importante del calentamiento atmosférico proviene de la radiación terrestre de longitud de onda larga, porque el flujo de calor latente es una contribución secundaria y el flujo de calor sensible sólo es importante en las regiones áridas donde no hay suficiente agua para la evaporación. Los océanos y los continentes también reciben indirectamente, irradiadas por la atmósfera, la mayor parte de su calor en forma de emisiones de longitudes de onda larga (4 – 50 μm). En este flujo de radiación reenviado hacia la superficie terrestre por los gases invernadero, domina a la radiación del vapor de agua, que con una concentración variable, emite entre 150 y 300 W/m2, y al que también contribuye el CO2 con unos 75 W/m2.

El intercambio de radiación de longitud de onda larga entre la superficie y la atmósfera sólo retrasa temporalmente las emisiones de calor terrestre, pero controla la temperatura de la biosfera. Su máximo es casi 400 W/m2 en los trópicos nubosos, pero es importante en todas las estaciones y presenta significativas variaciones diarias. El simple paso de una nube puede aumentar el flujo en 25 W/m2. Las mayores emisiones antropogénicas de gases invernadero han aumentado este flujo en cerca de un 2’5 W/m2 desde finales del siglo XIX.

Como era de esperar, las observaciones de los satélites confirman que el balance de energía de la Tierra está en fase con la radiación solar incidente (Q0), pero la radiación media saliente (Qi) está desfasada con la irradiancia, alcanzando el máximo durante el verano en el hemisferio norte. La distribución asimétrica de los continentes y el mar explica este fenómeno. En el hemisferio norte, debido a la mayor proporción de masa terrestre, se experimentan mayores cambios estacionales que dominan el flujo global de la radiación saliente.
Quizás el resultado más sorprendente que se deriva de las observaciones por satélite sea que, estacionalmente, se observan cierto déficit y superávit de radiación y el balance de la radiación en el planeta no es igual a cero, pero sin embargo, en cada hemisferio la radiación anual está en equilibrio con el espacio exterior. Además, la contribución atmosférica por transporte de energía hacia los polos es asimétrica respecto al ecuador con valores extremos de unos 3 PW cerca de los 45º N, y -3 PW cerca de 40º S.
Podría continuar hablando sobre los vientos, los terremotos, las lluvias y otros fenómenos atmosféricos, sin embargo, no creo que, por ser estos fenómenos naturales muy conocidos de todos, pudieran tener gran interés. Pasemos pues a comentar sobre los océanos.

El agua de la vida
Agua, mejor que Tierra, habría sido el nombre adecuado para el tercer planeta, puesto que los océanos cubren más del 70 por ciento de la superficie terrestre, con una profundidad media de 3’8 Km. Debido a las especiales propiedades térmicas del agua, éstas constituyen un extraordinario regulador del balance energético del planeta.
Este líquido tiene cinco ventajas termodinámicas importantes: un punto de ebullición inusualmente alto, debido a su capacidad para formar enlaces de hidrógeno intermoleculares; un calor específico de 2’5 a 3’3 veces más elevado que el del suelo; una capacidad calorífica (calor específico por unidad de volumen) aproximadamente seis veces mayor que la tierra seca; un altísimo calor de vaporización que le permite transportar una gran cantidad de calor latente; y su relativamente baja viscosidad, que le convierte en un eficiente transportador de calor en los océanos mediante miríadas de remolinos y caudalosas corrientes.

Los océanos de la Tierra vistos desde el espacio
No es sorprendente, pues, que los océanos, que tienen cerca del 94 por ciento de toda el agua, sean determinantes en el balance energético del planeta. Cuatro quintas partes de la radiación solar que llega a la Tierra entra en la atmósfera que cubre los océanos, los cuales con un albedo superior al 6% absorben la energía con una tasa cercana a 65 PW, casi el doble de la absorción atmosférica total y cuatro veces mayor que la continental. Inevitablemente, los océanos también absorben la mayor parte, casi dos tercios, del calor rerradioirradiado hacia abajo por la atmósfera elevando su ritmo de calentamiento a los 175 PW.
Salvo en los océanos menos profundos, la interacción aire-mar no afecta directamente a las aguas profundas. Las oscuras y frías aguas de las profundidades marinas están aisladas de la atmósfera por la capa mixta, una capa de poca profundidad que va de pocos metros a pocos cientos de metros y que está afectada por los vientos y el oleaje.
A pesar de que el alto calor específico del agua limita el rango de variación, las temperaturas de esta capa sufren importantes fluctuaciones diarias y estacionales. Sin embargo, variaciones relativamente pequeñas de la temperatura de la superficie de los océanos tienen importantes consecuencias climáticas: quizás el mejor ejemplo de esta teleconexión climática sea el fenómeno del Niño, que consiste en una extensión en forma de lengua de las aguas superficiales calientes hacia el este, cuyos efectos se extienden desde Canadá hasta África del sur.

En esta “coreografía” acuática, también tiene un papel significativo el Estrecho de Dinamarca, que se alimentan de las aguas más profundas de la AMOC y las devuelve al sur a través de brechas en la cordillera de Groenlandia y Escocia. En este sentido, los científicos explican que, durante años, se ha pensado que el estrecho danés, que ha aumentado considerablemente su capacidad como consecuencia del deshielo, se abastecía de una corriente adyacente a Groenlandia.
Debido a que la conductividad térmica del agua es muy baja, la transferencia de energía de la capa mixta hacia las profundidades se realiza fundamentalmente mediante corrientes convectivas. Estas corrientes compensan la extremadamente baja fuerza ascensional de las aguas profundas, más calientes, que son desplazadas por el movimiento hacia el ecuador de las corrientes frías provenientes de los polos. En contraste con el gradual ascenso general de las aguas oceánicas, la convección hacia abajo se produce en corrientes bien delimitadas que forman gigantescas cataratas oceánicas. Seguramente la mayor es la que fluye hacia el sur bajo el estrecho de Dinamarca, entre Islandia y Groenlandia, y se sumerge unos 3’5 Km transportando 5 millones de m3/s, un caudal veinte veces mayor que el del Amazonas.
Miríadas de corrientes oceánicas, que a menudo viajan cientos de kilómetros a diferentes profundidades, transportan considerables cantidades de energía y sal. Quizás el ejemplo más importante de estas combinaciones de transportes sea la corriente de agua caliente y salada que sale del Mediterráneo a través del estrecho de Gibraltar. Este flujo caliente pero denso desciende sobre la pendiente de la plataforma continental hasta alcanzar el equilibrio entre el peso y el empuje ascensional a unos mil metros de profundidad. Aquí se separa en dos celdas lenticulares que se mueven durante siete años hacia el este y hacia el sur, respectivamente, hasta que decaen o chocan contra alguna elevación marina.

Si el Estrecho de Gibraltar pudiera contar su historia… Es la ruta maritima más transitada del mundo
Un mapa global de los flujos de calor desde la superficie oceánica hasta las capas profundas muestra claramente máximos longitudinales a lo largo del ecuador y a lo largo de aproximadamente 45º S en los océanos Atlántico e Índico. Esta transferencia es también importante en algunas áreas costeras donde se producen intensos flujos convectivos ascendentes que intercambian calor entre las aguas superficiales y las profundas, como ocurre en la costa de California y al oeste de África. Un flujo en dirección contraria, que calienta la atmósfera, se produce en las dos mayores corrientes oceánicas calientes, la corriente del Golfo en el Atlántico y la de Kuroshio en el Pacífico oriental.
Todas la regiones donde se produce este ascenso de aguas calientes (a lo largo de las costas del continente americano, África, India y la zona ecuatorial del Pacífico occidental) se distinguen fácilmente por los elevados niveles de producción de fitoplancton, causados por un importante enriquecimiento de nutrientes, comparados con los que, de otra manera, corresponderían normalmente a las aguas superficiales oligotrópicas.
La radiación transporta la mayor parte (casi 4/5) de la energía que fluye desde la capa mixta hasta la atmósfera, y el resto del flujo calorífico se produce por calor latente en forma de vapor de agua y lluvias.

Océano Atrlántico
Aún no se ha realizado una valoración cuantitativa del transporte total para cada latitud, pero en el océano Atlántico hay transferencia de calor hacia el norte a lo largo de toda su extensión, alcanzando en el trópico un valor aproximado de 1 PW, flujo equivalente al que se produce en el Pacífico norte. En el Pacífico sur, el flujo de calor hacia el polo a través del trópico es de 0’2 PW. La parte occidental del Pacífico sur puede constituir la mayor reserva de calor del Atlántico sur, de igual modo que es probable que el océano Índico sur constituya una reserva del Pacífico.
Ahora tocaría comentar algo sobre los ríos del planeta, sin embargo, lo obvio y me dirijo directamente a comentar sobre el calor de la Tierra.
Aunque la Tierra se formara inicialmente a partir de materia fría (material cósmico) que se contrajo por acción de la gravedad, durante la formación posterior del núcleo líquido y en los periodos de intensa actividad volcánica se ha liberado una enorme cantidad de calor. Los frecuentes impactos de objetos pesados también han contribuido al calentamiento de la superficie. Hay mucha incertidumbre sobre la historia térmica de la Tierra de los últimos 3.000 millones de años, durante los cuales el planeta se ha ido enfriando y una gran parte de este flujo de calor ha alimentado los movimientos geotectónicos globales, creando nueva corteza en las dorsales oceánicas; un proceso que ha ido acompañado de terremotos recurrentes y erupciones volcánicas de lava, cenizas y agua caliente.

Solamente hay dos posibles fuentes de calor terrestre, pero la importancia relativa de las respectivas contribuciones no está aún muy clara. El calor basal, liberado por un lento enfriamiento del núcleo terrestre debe representar una gran parte del flujo total, si bien cálculos basados en la desintegración radiactiva del U235, U238, Th232 y K40 sugieren que éste representa al menos la mitad y quizás hasta nueve décimos del flujo total de calor del planeta. Esta disparidad obedece a la incertidumbre en la concentración de K40 en la corteza terrestre. Pero sea cual sea la proporción, el flujo total, basado en miles de medidas realizadas desde los años cincuenta, está próximo a los 40 TW.
Aunque inicialmente se pensó que los flujos continentales y oceánicos eran aproximadamente iguales, en realidad difieren de forma sustancial. Las regiones del fondo oceánico más recientes contribuyen con más de 250 mW/m2, cantidad que supera hasta tres veces las zonas continentales más recientes. El flujo medio para todo el fondo marino es aproximadamente igual a 95 mW/m2, lo que representa un 70% más que el correspondiente a la corteza continental. El flujo medio global es de 80 mW/m2, unos tres órdenes de magnitud inferior al valor medio del flujo de calor de la radiación solar global.
Publica: emilio silvera
La fuente del presente trabajo, aunque variada en texto e imágenes, en su mayor parte está en una guía ilustrada de la biosfera y la civilización de Vaclav Smil.
















 Totales: 74.825.057
Totales: 74.825.057 Conectados: 37
Conectados: 37





















