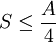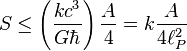“EL METODO DE LA CIENCIA, EL OBJETIVO DE LA RELIGION”    Aleister Crowley.Hoy día existe un debate fundamental acerca de la comprensión del Universo. Este debate tiene lugar entre los racionalistas y los metafísicos y sus maneras opuestas de contemplar el mundo. Se supone que sólo puede quedar uno; Que la explicación final del universo  ha de tener un resultado determinado. Por lo tanto la pregunta de si podría existir un punto de encuentro entre ambos es negativa, ya que es contrario a las creencias de unos y otros.

Desde muy antiguo hemos sido educados pensando que tan sólo puede existir una verdad y, como consecuencia de esta creencia, hemos inventado en cada época un modo adecuado para satisfacerla.
El modo que hemos empleado en cada momento se podría decir que es la herramienta conceptual, el criterio de veracidad para dar sentido a ese concepto tan difuso que denominamos verdad. Pero, en esta herramienta o modo de pensamiento hay algo que nunca ha cambiado y es que siempre hemos exaltado a una especie de divinidad imaginaria, algo que nos ha permitido entender (o dar sentido) por completo al mundo, aun cuando su argumento sea irracional.

Lo único que ha cambiado con el tiempo  es nuestro criterio o nuestra forma de validar lo que es o no cierto…. Pero no se nos ha permitido cambiar nunca la regla fundamental: la existencia de una divinidad.
Relativizando el asunto podemos entenderlo con un ejemplo. Hoy tildamos de irracionales a los metafísicos, con el pretexto de que no pueden demostrar ninguno de sus argumentos. En otros tiempos tildamos de irracionales a los nativos de otras culturas, al mismo tiempo que dábamos sentido a un Dios capaz de reencarnarse en forma humana. Parecen argumentos muy distintos, pero el sentido es el mismo.

Hoy día a esta divinidad imaginaria la denominamos teorema, y es la forma básica de condensar nuestra lógica matemática. Nunca nadie y en ningún momento de la historia ha podido contradecir la lógica de un teorema matemático. De hecho, es imposible hacerlo siempre que convengamos que sus reglas son ciertas en todo momento.

Por lo tanto, tienen razón los racionalistas. Jamás los metafísicos podrán demostrar ninguna de sus propuestas. La única forma de hacerlo sería incumpliéndolas. Ahora bien, esto supone ir contra una especie de regla universal, más antigua incluso que nuestra aceptación de la divinidad; Y es que, como todos sabemos, las matemáticas son perfectas para entender el Universo.

De acuerdo con Buckminster Fuller, no debemos intentar cambiar un sistema, tenemos que construir uno nuevo, que haga que el anterior se vuelva obsoleto. En otras palabras, si no puedes con tu enemigo únete a él, descubre cómo piensa y cambia sus creencias.

Einstein ya lo hizo. Este científico, con su teoría de la relatividad se saltó las reglas matemáticas y cambio el sistema. Él estaba convencido de que las matemáticas eran perfectas para describir todo cuanto sucede en su mundo lógico e imaginario, pero que eran incompletas para describir la realidad.

Este argumento se conoce como “incompletitud” y establece que ningún sistema  puede decir nada acerca de su propia existencia y que, en consecuencia, todo lo que diga sobre ella será simplemente una creencia, una fe irracional. Siempre habrá una respuesta por imposible que parezca que no podremos demostrar utilizando la herramienta matemática, una respuesta que (aunque exista) no podremos decir nada de ella.

Por eso los metafísicos también tienen razón en sus planteamientos. A esta posibilidad de que exista un plano inmaterial de la realidad, algo que no podemos detectar (aunque intuyamos que pertenece a la realidad) la denominamos una respuesta fuera del sistema. Se podrá estar en contra de ella, pero lo cierto es que no existe ningún criterio lógico de pensamiento que desmienta ninguna de sus afirmaciones. Prueba de ello es nuestra tendencia creciente a admitir (más allá de un argumento racional) que la mente crea la realidad.

Esto sucede porque los racionalistas se suponen exentos de la carga de la prueba. Según ellos es la otra parte la que debe demostrar de forma racional la existencia de su divinidad, ese plano metafísico o inmaterial de la realidad, ese plano en el que según ellos todos estamos conectados.

No podemos, por tanto, decir nada acerca de la existencia de un sistema, no podemos usar sus reglas para demostrar que son incorrectas, este es el método circular de pensamiento que hace que sea inútil el  enfrentamiento. Por lo tanto, debe de ser cierto que desde dentro no podemos hacer nada, tenemos que salirnos fuera de su sistema de creencias. Tenemos que crear un nuevo sistema.
El racionalista siempre te pedirá que demuestres la existencia de ese plano inmaterial de la realidad. El problema, por tanto, es: ¿quién pone las herramientas para hacer esto? Para el racionalista la única regla valida o herramienta son las matemáticas, básicamente porque establecen la presunción de que no puede haber otra.

Matemáticamente existen unos pocos métodos de demostración. Todos ellos solemos aprenderlos en la adolescencia, en un periodo en que pasamos de la infancia a la edad adulta y en el que solemos estar interesados en otras cosas. Realmente es el peor momento para pensar en contradecir la regla lógica. No la cuestionamos y de esta manera pasa a formar parte de nuestras creencias.

Todos los métodos de demostración matemática se basan en que será correcto todo lo que hagamos en matemáticas si nunca incumplimos las reglas…. Lo que representa realmente un absurdo en sí mismo: un sistema circular.

Alternativamente consideramos la “reducción al absurdo” o el contraejemplo, como una manera alternativa de demostración matemática. De acuerdo con este método de pensamiento es absurdo todo aquello que contradiga la regla matemática que, en su esencia, es ésta: “Una solución no puede ser nunca igual a su opuesta”

Realmente todos los métodos de demostración matemática tienen el mismo comportamiento: es una absurdidad todo lo que no se pueda demostrar siguiendo este criterio de veracidad.

Poner en cuestión la regla matemática pasa por contradecir su principal premisa lógica. Decir que una solución no puede ser igual a su opuesta, es algo equivalente (conceptualmente) a decir que una unidad matemática ha de ser a-dimensional, es ella y nada más: una única verdad. Por eso en matemáticas decimos que un punto no tiene dimensión, que no existe en realidad.

Pero, resulta que las matemáticas son profundamente contrarias al funcionamiento de la realidad. Físicamente una unidad nunca ha sido ni será a-dimensional. En la naturaleza no se da nunca una única respuesta, todo lo más que hemos podido decir de ella es que sus resultados siempre son indeterminados, dos posibles estados.

La relatividad es un ejemplo perfecto, pero es lo mismo que pasa en el mundo cuántico cuyo único principio básico es que nada puede ser estrictamente definido, que todo es indeterminado. La teoría del Big-Bang también ahonda en este concepto: todo nuestro universo puede ser reducido de forma conceptual (y, en consecuencia, matemática) a un punto inicial. Por lo tanto lo contrario también puede ser cierto: “Un punto puede contener todo un Universo”

Quizás el ejemplo más claro de la indeterminación, relatividad o probabilidad en que se basa el Universo sea el cuanto de Planck. Normalmente decimos de él que es la unidad mínima en que podemos cuantificar el Universo ¡Y es cierto!… Pero resulta que un cuanto de Planck, aunque sea una unidad, no es a-dimensional,  sino que es capaz de expresarse en varias dimensiones diferentes: longitud de Planck, tiempo de Planck, etc…

Realmente nuestra concepción matemática más básica es contraria a la percepción que tenemos del funcionamiento del Universo: la dualidad del espacio-tiempo o del futuro y el pasado.
Este plano inmaterial de la realidad ya ha sido puesto de relieve en múltiples experimentos, no sólo la mecánica cuántica es un ejemplo, también los agujeros negros, la energía oscura que permea el Universo, etc…

Bajo el criterio metafísico no tiene sentido tratar de detectar el plano inmaterial, esto es una absurdidad. No tiene sentido colisionar partículas fundamentales para tratar de encontrar patrones de comportamiento inmateriales. Para los racionalistas este criterio no es válido argumentando con el pretexto de qué es cuestión de tiempo que podamos hacerlo.  Siguiendo el método matemático al final obtendremos las respuestas que queremos o si no nos las inventaremos: tan sólo tenemos que cambiar el nombre para ello. Detrás de este razonamiento existe el convencimiento (irracional) de que todo tiene un principio y un final y, en consecuencia, todo es susceptible de ser calculado.

No pensamos que pueda haber otras explicaciones de la realidad, no damos sentido a su existencia, pero esto únicamente sucede como consecuencia de nuestras creencias. Nos sometemos a un criterio de verdad absoluta y pensamos que no puede haber otro método de demostrar la realidad. El pensamiento racional es éste, ¿cómo podría haber otro criterio más completo si las matemáticas son perfectas para describir la realidad y todas nuestras leyes físicas se basan en ellas?

¿Cómo podemos salir de un argumento circular? Lógicamente creando un nuevo paradigma de pensamiento, una forma de pensar absurda e irracional, y completamente opuesta a las creencias matemáticas.
El truco para hacerlo es el mismo que se ha empleado desde antiguo: Se trata de crear un sistema de pensamiento circular pero que sea consistente consigo mismo. Será irracional… ¡Y estamos de acuerdo! Pero… es que el método matemático también sigue el mismo principio. Tan sólo es racional lo que está dentro de su esfera de conocimiento.

La cuestión por tanto es… ¿Podemos crear otra esfera de conocimiento tan consistente como la esfera matemática, siendo a su vez opuesta a ella?

Lo cierto es que podemos hacerlo. La única condición que hemos de tomar en consideración es que dicha solución sea siempre opuesta a ellas. En esencia, este sería el razonamiento:

La reducción al absurdo matemática establece que una solución opuesta al sistema es irracional, dado que nunca será capaz de ofrecer una respuesta determinada. En oposición, el criterio opuesto (el metafísico) establece que todo es indeterminado y que, precisamente, ésta es la respuesta: la ausencia perpetúa o eterna en el Universo de un resultado determinado. La viabilidad de esta respuesta está fundamentada en la existencia del eterno movimiento. Es lo que conocemos como principio de indeterminación: dado que todo se está moviendo no podemos establecer nunca con absoluta precisión el movimiento y la posición de una partícula.

En el fondo el criterio metafísico también es irracional, dado que un sistema basado eternamente en la dualidad en el fondo sigue una regla, una regla determinada de comportamiento. Se trata de un sistema irracional.

Es decir, el criterio metafísico establece que no hay nada en el universo que sea independiente, y existe una ley que es universal, y esta ley es la relatividad o la ley del eterno movimiento.

Einstein incumplió las reglas, porque introdujo el movimiento como elemento necesario en sus ecuaciones. El movimiento es contrario a la existencia de un teorema matemático, dado que por definición es estático. Un teorema matemático como el cálculo de una fuerza no es más que un flash, una foto puntual, la condensación en un plano estático de un patrón de funcionamiento, o la comparación aritmética entre dos instantes diferentes de tiempo.

¿Cómo funciona, en esencia, nuestro criterio de veracidad?

Un teorema matemático establece que podemos “recorrer” dos caminos (o funciones matemáticas) diferentes para llegar a un mismo resultado. El teorema matemático presupone de inmediato que un resultado es algo unitario o determinado. El criterio metafísico establece que esto no es cierto, dado que no podemos establecer si el Universo tuvo un principio o un final. Y es matemáticamente no podemos ir más allá, todo lo que supongamos a partir de este punto no será racional. El criterio metafísico establece que no se acaban nunca estos caminos, que existe el perpetuo movimiento en el Universo y que, por lo tanto, todo resultado siempre será indeterminado.

El problema subyacente es que no entendemos el cambio de estado como un movimiento del Universo, dado que matemáticamente no es posible hacerlo. Matemáticamente tan sólo cuantificamos entre diferentes estados, que es exactamente lo que hacemos cuando calculamos una fuerza. Matemáticamente tan sólo trabajamos con un universo estático. Y es difícil advertir las limitaciones de este sistema de pensamiento.

Aún cuando somos conscientes de que podemos acotar una solución con infinitos términos, no consideramos que esto sea un criterio de veracidad.

Por ejemplo, la sucesión de Basilea (una de las sucesiones matemáticas más famosas) (una sucesión matemática es un continuo de infinitos términos que nunca se acaba) establece que la suma de los inversos de los cuadrados de los infinitos números enteros que componen la recta real tiende a la forma de una circunferencia. Este es un resultado impresionante y que hemos incorporado como base a algunas de nuestras más importantes conjeturas matemáticas. Pero, lamentablemente, debido al axioma de verdad matemática, lo cierto es que con ella no hemos podido demostrar nada de forma concluyente.

De hecho, muchas de las más importantes conjeturas ahondan en este concepto. No se pueden demostrar, porque precisamente su resultado es incompatible con las reglas matemáticas. Podemos entender esto con un ejemplo:

Una de nuestras más importantes conjeturas establece la posibilidad de que podamos expresar siempre la complejidad de forma simplificada. Podemos entender esto diciendo (en palabras de fuller) que el mejor diseño es hacer lo máximo con lo mínimo. El mejor diseño implica por tanto la máxima eficiencia. Y, curiosamente, así es como se expresa siempre la naturaleza. Tan sólo tenemos que observar la forma de una esfera.

Si esto fuera cierto ¿Cuál sería la forma más simplificada de hacerlo? Lógicamente el criterio de que todo ha sido siempre y será indeterminado es la mejor manera de lograrlo, dado que únicamente requiere la presencia de dos elementos: de forma genérica, un elemento y su opuesto. La regla de indeterminación es una regla genérica y, por lo tanto, es perfecta para describir un patrón de comportamiento. Como dije antes una regla infinitamente indeterminada en el fondo sigue una regla, es un sistema.

Tan sólo incumplimos una regla matemática, pero su más regla básica, cuando decimos que todo elemento en el Universo (real o matemático) tiene siempre su supuesto. Esto implica un universo súper-simétrico o equilibrado… el Universo como un reflejo de si mismo…. Un universo matemático y a la vez físico.

Observa que un patrón indeterminado la regla es ésta: la condición de inicio es igual a la condición final. Si nada puede contradecir esto como sistema de creencias, esta regla será universal. La podemos contemplar, por tanto, como si de un teorema se tratara. La parte irracional es que siempre tendremos el infinito como resultado. Pero es que para los metafísicos el infinito es la respuesta.

La cuestión final es ésta ¿Podemos compactificar un sistema irracional y basado siempre en el infinito o principio de la eterna dualidad, de tal manera que ésta sea siempre su regla de comportamiento?

Si podemos hacerlo habremos creado una respuesta que tendrá un resultado determinado, habremos creado un sistema, una unidad o un universo matemático geométrico e imaginario.  Este universo tendrá dos planos, un plano real y otro imaginario. Habremos creado un sistema opuesto al sistema matemático, pero sin violar el principio de relatividad, que siempre establece que necesitamos dos puntos de vista para entender la realidad.

Paradójicamente la que conocemos como la fórmula matemática más bella del Universo, la identidad de Euler, nos dice que esto es cierto. Podemos crear un sistema matemático completamente irracional que siempre tienda a una identidad. Y para ello tan sólo tenemos que dar sentidos a dos planos opuestos de la realidad. Y es que… genéricamente la identidad de Euler expresa la forma de condensar una realidad matemática infinitamente irracional en una forma acotada, algo que bajo nuestro punto de vista no deja de ser un resultado determinado.

La identidad de Euler nos da un patrón de entrelazamiento dimensional, nos dice que el Universo es un fractal que, en último término se puede sintetizar en la forma de una unidad. Esta unidad no es un punto de inicio ni un punto final (como el big-bang, o el big-crash) sino que tiene su propio movimiento. Ahora bien, este movimiento es opuesto al movimiento que observamos en el Universo, es un movimiento transversal, un movimiento que jamás podremos detectar porque opera en un plano diferente de la realidad.

Este plano inmaterial de la realidad es nuestro sentido del tiempo, y es la señal que nos indica que todo lo que es verdad se ha de basar en el movimiento. Lo contrario también es cierto, pero sólo puede explicar la parte más material de la realidad.

Porque…. ¿Cómo vamos a concebir un tiempo tridimensional, si desde pequeños nos han enseñado que el tiempo es lineal?  Siempre nos han enseñado la gran utilidad de comparar entre dos instantes diferentes de tiempo o cambios de estado, pero nunca nos han enseñado que tiene poco sentido hacerlo. El Universo es independiente de nuestros sistemas de medida, realmente hacer esto es irrelevante a nivel universal.

Siempre y en todo momento podemos condensar el movimiento del Universo de forma cíclica. Siempre podremos decir que cada ciclo es una unidad temporal, y que por tanto realmente tiene poco sentido referirnos a un tiempo lineal. La noción de tiempo lineal es un concepto que tan sólo está en nuestras mentes, una creencia implantada, pero que no se corresponde en global con la realidad. De hecho, como sabemos, siempre podemos transformar una escala espacial tridimensional en una medida temporal basada en ciclos o secuencias acotadas: hacemos esto cuando expresamos los números como ejes espaciales en forma polar.

Pero, aunque sea posible determinar una coordenada espacial en función de tres ciclos de tiempo, seguimos pensando que el tiempo es lineal. Al adoptar sistemas de medidas, sean los que sean, siempre hacemos esto, tratamos de acotar el tiempo de forma irracional. Las coordenadas GPS serían un ejemplo.

Como consecuencia de no adoptar un criterio absolutamente genérico, y utilizar uno arbitrario tratamos de detener el tiempo y el resultado que obtenemos siempre es éste: “Error del sistema, infinito, indeterminado”. Cualquier variable que introduzcamos para describir el Universo siempre ha acabado de la misma manera: no ha hecho falta, era innecesaria. El mundo cuántico, que tan sólo se basa en la probabilidad, sería un ejemplo perfecto: ningún criterio humano es necesario.

El “Libro de los Muertos” dice en el capítulo 112: “El Ojo de Horus es tu protección, Osiris, Señor de los Occidentales, constituye una salvaguarda para ti: rechaza a todos tus enemigos, todos tus enemigos son apartados de ti”. Un pasaje que recuerda realmente a la apertura del Mar Muerto; O ¿Por qué no?, a la regla roma de “Divide y vencerás”. Crea escalas y más escalas a fin de que no pueda verse nunca la realidad.

La leyenda dice que el libro de los muertos fue escrito por Thot, el dios de la escritura y el conocimiento. Contiene dos encantamientos, uno de los cuales, supuestamente, permite, a quien lo lea, percibir a los dioses por sí mismo.

La historia de la dualidad es la historia del eterno simbolismo egipcio. Y es que… de acuerdo con ellos, para conseguir la “vida eterna” los elementos opuestos han de estar siempre equilibrados. Es la eterna ley, es la regla. Y este es su símbolo: “la balanza”.

¿Podemos por tanto condensar la “vida eterna” de forma genérica, podemos condensar el infinito matemático de forma geométrica? Tanto la identidad de Euler como los egipcios nos dicen que es posible hacerlo, pero resulta que matemáticamente se nos cierra la puerta, porque el infinito no es respuesta. Y este…  es un error del sistema, una anomalía.

En consecuencia para romper la regla lo único que tenemos que hacer es tender a la unidad, crear todo un sistema basado en ella, y no sólo en la dualidad. ¿Cómo saber algo que no sabemos? ¿Cómo saber que no estamos manipulados, si desde que tenemos uso de razón siempre hemos estado gobernados?

Todo está en equilibrio, porque todo se basa en el permanente cambio de estado. Donde unos ven algo determinado, otros ven algo que nunca empieza y acaba. Pero supongo que estaremos de acuerdo en que no hay nada que pueda detener el movimiento de una onda.