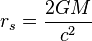Oct
3
Nuestra percepción y la realidad: Dos cosas distintas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (2)
Comments (2)

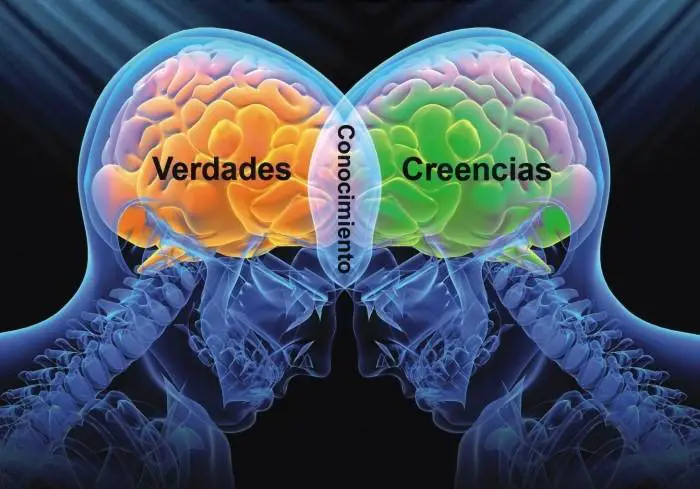
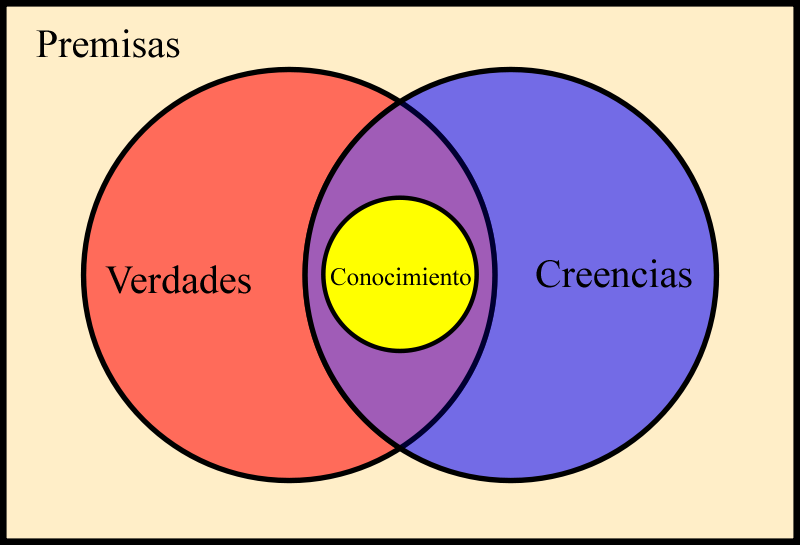
Nuestra realidad es que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno posee su propia realidad del mundo y de él mismo. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las “culpables” de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestra educación, nuestro entorno, nuesstra preparación, nuestra capacidad intelectual…

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”
Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.
Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarnos más y más a esa realidad que presentimos, y de esa manera encontramos la forma de aproximarnos a esa realidad intuida. En la vida cotidiana, en el hombre de la calle, se halla muy extendido el Practicismo o Realismo ingenuo, se admite, sin más reflexión, que la realidad existe y no se plantean el problema de cuestionar tal existencia. Sin embargo, para los filósofos, el problema de la existencia o no de la Realidad Metafísica y la certeza sobre el conocimiento que sobre ella extraen nuestros sentidos (Epistemología) ha sido, desde los primeros filósofos griegos (pre-socráticos), y continua siendo, uno de los grandes problemas filosóficos que todavía no ha sido resuelto. Es decir, una cuestión sobre la que no tenemos respuesta unánimemente aceptada por todos los pensadores.

Los humanos, desde que fuimos conscientes de nuestro Ser, hemos estado desarrollando diferentes corrientes de pensamientos filosóficos (o doctrinas) que han tratado de responder al problema de si existe o no la realidad fuera de nuestra mente. Películas actuales como “Matrix” es una buena muestra de que el problema de la realidad todavía nos tiene intrigados a los seres humanos de hoy.
La epistemología es una rama de la filosofía que se ocupa de la validez y fiabilidad de los conocimientos que obtenemos los humanos. Viene a ser como una teoría crítica del conocimiento. Desde el punto de vista epistemológico se han planteado cuestiones tales como:
- ¿Se corresponde la realidad con larepresentación mental que el hombre tiene? ¿O el mundo psíquico es un producto inventado por la mente humana?
- ¿Es fiable y válida la información que los órganos sensoriales captan? ¿O nos engañan nuestros sentidos?
- ¿Cómo llegamos a tener conciencia de la existencia de un espacio poblado de objetos y sujetos (mundo)?
- ¿Es realmente el Universo, como nosotros lo percibimos, o, siendo nuestros sentidos imperfectos nos muestra un universo diferente al que es?

No todos perciben “el mundo” de la misma manera. Tampoco resuelven sus problemas de igual forma

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado y sobre ese objetivo en particular.
Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas y conceptos conseguir sus teorías que están muy cercas de lo que el mundo es.
Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un concreto.
El eterno e irracional número Pi
Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:
1 – 1/3 + 1/5 – 1/7 ….
Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente, se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, No obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y entre otros temas. Si hablamos de “Pi” nos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN, el Efecto mariposa y la Torah, entre otras muchísimas cosas que se escriben con Pi. Es un número tan misterioso que lo podemos ver por todas partes representado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.
No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada , que deducir el mundo. Yo no dejaría de lado, en todo esto la teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus inicios. El ejemplo más común es conocido como “Efecto mariposa”. La teoría supone que el batir de alas de una mariposa en la China en un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.
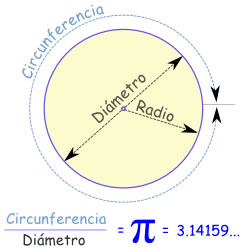
Pi (π) es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.
El escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.
Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han buscando un patrón en el cordón interminable de números.
Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece muy cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.
¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la /patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.
3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th
Muchos son los números mágicos que, como Phi, al que llaman ¡El Mágico Número del Oro! Están relacionados con las cosas del mundo, del universo y de nosotros mismos. Como decían enm la Escuela pitagórica: ¡Todo es número!
1, 2, 2+1= 3, 3+2= 5, 5+3= 8, 5+8= 13 , etc.


¿Por qué los huracanes, remolinos, galaxias y agujeros negros desarrollan su dinámica en base a la proporción aúrea?

¿Saben que las dimensiones físicas del cuerpo humano cumplen también las relaciones de aspecto dadas por 1,6180…?
¿Cómo es posible que el vuelo de una rapaz al acecho también describa la elipse marcada por esta serie?

¿Por qué la ciudad de La Meca está ubicada en la posición geográfica cuya distancia a los Polos y a los solsticios cumple la relación PHI?
Podemos incluso encontrar esta asombrosa serie en la relación de aspecto de la espiral de adn y en los latidos del corazón.


Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra , existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejmplo:
Roger Penrose dedicó bastante más tinta en defender los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.
Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos por lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

¿Es la verdad inalcanzable?
Sin embargo, Roger Penrose, piensa que no, y demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.
Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos , somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos y dispares pensamientos:
- Los Computadores nunca podrán reemplazar la estupidez humana.
- El hombre nace ignorante, la educación lo idiotiza.
- Una persona inteligente resuelve problemas, el genio los evita.
- Las consideran que guardar un secreto, es no revelar la fuente.
- Todas las mujeres tienen algo bonito… así sea una prima lejana.
- La felicidad es una lata de atún, con el abrelatas un poco distante.
- El único animal que no resiste aplausos es el mosquito.
- El amor está en el cerebro, no en el corazón.
- Definición de nostalgia “es la alegría de estar triste”.
- “Mi segundo órgano favorito es el cerebro”.

En qué se parecen los hombres a una computadora: En que cuando más lo necesitas, se les cae el sistema.
Vale, ¿y qué consecuencias tiene eso? la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos construir un modelo matemático, qué menos que intentar replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos.
De misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.
Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…
O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!
Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?
Todo eso está bien pero, ¿Qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. cuadrado tiene el mismo área que el circulo”.

Oct
3
De estrella masiva a Agujero Negro
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (0)
Comments (0)
Cuando hablamos de un agujero negro estamos hablando de un objeto con un campo gravitacional tan intenso que su velocidad de escape supera la velocidad de la luz. Los agujeros negros se forman cuando las estrellas masivas colapsan al final de sus vidas. Un objeto que se colapsa se convierte en un agujero negro cuando su radio se hace menor que un tamaño crítico, conocido como radio de Schwarzschild, y la luz no puede escapar de él.
La superficie que tiene este radio crítico se denomina horizonte de sucesos, y marca la frontera dentro de la cual esta atrapada toda la información. De esta forma, los acontecimientos dentro del agujero negro no pueden ser observados desde fuera. La teoría muestra que tanto el espacio como el tiempo se distorsionan dentro del horizonte de sucesos y que los objetos colapsan a un único punto del agujero, que se llama singularidad, situada en el propio centro del agujero negro. Los agujeros negros pueden tener cualquier masa.
Pueden existir agujeros negros supermasivos con cientos de miles de masas solares, verdaderos montruos, en los centros de las galaxias activas. En el otro extremo, miniagujeros negros con un radio de 10-10 m y masas similares a las de un asteroide pudieron haberse formado en las condiciones extremas que se dieron poco después del Big Bang.
El proceso comienza al final de la vida de las estrellas que, dependiendo de sus masas, serán enanas blancas, estrella de neutrones, o, en último lugar, Agujeros Negros, los más masivos y densos. Se habla ahora de la existencia de las estrellas de Quarks que, de existir, estarían en el punto intermedio entre las de neutrones y los agujeros negros.
Nunca se ha observado directamente un agujero negro. Kart Schwarzschild (1.837 – 1.916), dedujo la existencia de agujeros negros a partir de las ecuaciones de Einstein de la relatividad general de 1.915 que, al ser estudiadas en 1.916, un año después de la publicación, encontró en estas ecuaciones que existían tales objetos supermasivos.
Antes, en la explicación sobre las estrellas, queriendo dejarlo para este momento, deje de explicar lo que hace el equilibrio en la vida de una estrella. La estrella está formada por una inmensa nube de gas y polvo que a veces tiene varios años luz de diámetro. Cuando dicho gas (sus moléculas) se va juntando se produce un rozamiento que ioniza los átomos de la nube de hidrógeno que se juntan y se juntan cada vez más, formando un remolino central que gira atrayendo al gas circundante, que poco a poco va formando una inmensa bola. En el núcleo, la fricción es muy grande y las moléculas apretadas al máximo por la fuerza de gravedad, por fin produce una temperatura de varios millones de grados K que es la causante de la fusión de los protones que forman esos átomos de hidrógeno. La reacción que se produce es una reacción en cadena; comienza la fusión que durará todo el tiempo de vida de la estrella. Así nacen las estrellas cuyas vidas están supeditadas al tiempo que tarde en ser consumido su combustible nuclear, el hidrógeno que mediante la fusión es convertido en helio.
Es estas regiones comienza la historia de lo que muchos millones de años más tarde, será un agujero negro. Estrellas nuevas supermasivas, azuladas y de intensa radiación ultravioleta (como esa que vemos abajo a la derecha), un día lejano en el tiempo llegará a su final y se convertirá en supernova, eyectará las capas exteriores de su masa al espacio interestelar y, el resto de la estrella, quedando libre de la fuerza de radiación que producía la fusión nuclear, quedará a merced de la fuerza de Gravedad que, haciendo su trabajo, la comprimirá hasta extremos insispechados convirtiéndola en un Agujero Negro. Si la masa es más pequeña (2 – 3 masas solares) será una estrella de neutrones, ya que, al ser comprimido los protones y electrones allí presentes, se fusionaran para convertirse en neutrones que, al sentirse estrechamente enpaquetados, se degenerarán e impedirán que la masa de la estrella siga comprimiéndose.
Las estrellas muy grandes, conocidas como supermasivas, son devoradoras de hidrógeno y sus vidas son mucho más cortas que el de las estrellas normales. Una vez que se produce la fusión termonuclear, se ha creado el equilibrio de la estrella; veamos como. La inmensa masa que se juntado para formar la estrella genera una gran cantidad de fuerza de gravedad que tiende a comprimir la estrella bajo su propio peso. La fusión termonuclear generada en el núcleo de la estrella, hace que la estrella tienda a expandirse. En esta situación, la fusión que expande y la gravedad que contrae, como son fuerzas similares, se contrarresta la una a la otra y así la estrella continua brillando en equilibrio perfecto.

Pero, ¿qué ocurre cuando se consume todo el hidrógeno?
Pues que la fuerza de fusión deja de empujar hacia fuera y la gravedad continúa (ya sin nada que lo impida) hasta conseguir que la masa de la estrella implosiones, es decir, caiga sobre sí misma contrayendose más y más hasta llegar a tener una demnsidad enorme y un radio mucho más pequeño que el original. El resultado final dependerá de la masa inicial y conforme a ella se produce la transición de fase hacia una u otra clase de estrella.
Según sean estrellas medianas como nuestro Sol, grandes o muy grandes, lo que antes era una estrella, cuando finaliza el derrumbe o implosión, cuando la estrella es aplastada sobre sí misma por su propio peso, tendremos una estrella enana blanca, una estrella de neutrones o un agujero negro.
Como si fuera una mariposa, esta estrella enana blanca comienza su vida envolviéndose en un capullo. Sin embargo, en esta analogía, la estrella sería más bien la oruga y el capullo de gas expulsado la etapa verdaderamente llamativa y hermosa. La nebulosa planetaria NGC 2440 contiene una de las enanas blancas conocidas más calientes. La enana blanca se ve como un punto brillante cerca del centro de la fotografía. Eventualmente, nuestro Sol se convertirá en una “mariposa enana blanca”, pero no en los próximos 5 mil millones de años. Las estrellas conocidas como “enanas blancas” pueden tener diámetros de sólo una centésima del Sol. Son muy densas a pesar de su pequeño tamaño.

Hermosas Nebulosas planetarias con una enana blanca en su centro
Sí, en el Universo son muchas las cosas que existen para nuestro asombro y, no pocas veces, nuestras mentes tienen que hacer un alto en el camino, para pensar profundamente, hasta llegar a comprender lo que allí existe y como llegó a poder formarse.
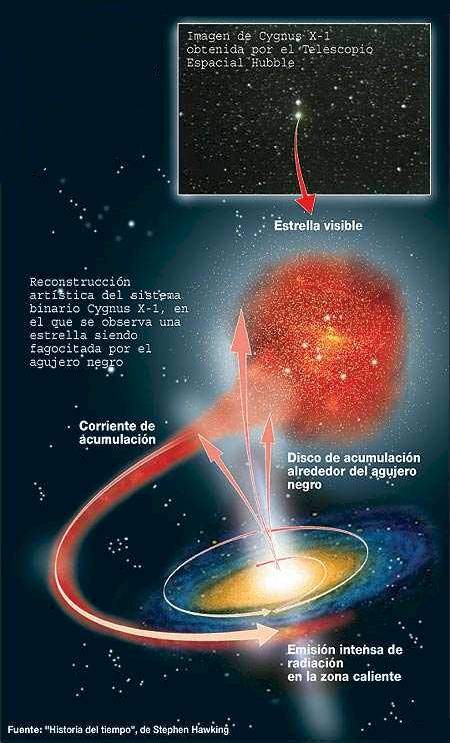
Alrededor del agujero negro puede formarse un disco de acreción cuando cae materia sobre él desde una estrella cercana que, para su mal, se atreve a traspasar el horizonte de sucesos. Es tan enorme la fuerza de gravedad que genera el agujero negro que, en tal circunstancias, literalmente hablando se come a esa estrella compañera próxima. En ese proceso, el agujero negro produce energía predominantemente en longitudes de onda de rayos X a medida que la materia está siendo engullida hacia la singularidad. De hecho, estos rayos X pueden ser detectados por satélites en órbita. Se ha localizado una enorme fuente de rayos X en el centro mismo de nuestra galaxia. En realidad han sido varias las fuentes localizadas allí, a unos 30.000 años luz de nosotros. Son serios candidatos a agujeros negros, siendo el más famoso Cygnus X-1.

Esta es una de las representaciones artísticas que nos hacen de Signus X-1. Es un ejemplo clásico de una Binaria de Rayos X, un sistema binario formado por un objeto compacto, que puede ser un agujero negro o una estrella de neutrones, y la estrella supergigante azul azul HDE 226868 de magnitud aparente 8,9. Como en toda binaria de rayos X, no es el agujero negro el que emite los rayos X, sino la materia que está a punto de caer en él. Esta materia (gas de plasma) forma un disco de acreción que orbita alrededor del agujero negro y alcanza temperaturas de millones de Kelvin que, quizás un día lejano aún en el futuro, podamos aprovechar como fuente de energía inagotable.

La técnica de la interferometría de muy larga base a longitudes de onda milimétricas (mm-VLBI) ha permitido obtener imágenes de los motores centrales de las galaxias activas con una resolución angular de decenas de microsegundos de arco. Para aquellos objetos más cercanos (M87, SgrA) se obtienen resoluciones lineales del orden de las decenas de Radios de Schwarzschild, lo que permite estudiar con detalle único la vecindad de los agujeros negros supermasivos.
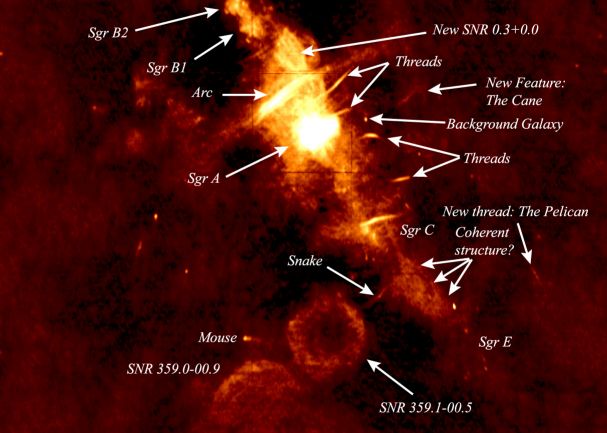
Al sintonizar hacia el centro de la Vía Láctea, los radioastrónomos exploran un lugar complejo y misterioso donde está SgrA que…¡Esconde un Agujero Nefro descomunal! Las observaciones astronómicas utilizando la técnica de Interferometría de muy larga base, a longitudes de onda milimétricas proporcionan una resolución angular única en Astronomía. De este modo, observando a 86 GHz se consigue una resolución angular del orden de 40 microsegundos de arco, lo que supone una resolución lineal de 1 año-luz para una fuente con un corrimiento al rojo z = 1, de 10 días-luz para una fuente con un corrimiento al rojo de z = 0,01 y de 10 minutos-luz (1 Unidad Astronómica) para una fuente situada a una distancia de 8 Kpc (1 parcec = 3,26 años-luz), la distancia de nuestro centro galáctico. Debemos resaltar que con la técnica de mm-VLBI disfrutamos de una doble ventaja: por un lado alcanzamos una resolución de decenas de microsegundos de arco, proporcionando imágenes muy detalladas de las regiones emisoras y, por otro, podemos estudiar aquellas regiones que son parcialmente opacas a longitudes de onda más larga.
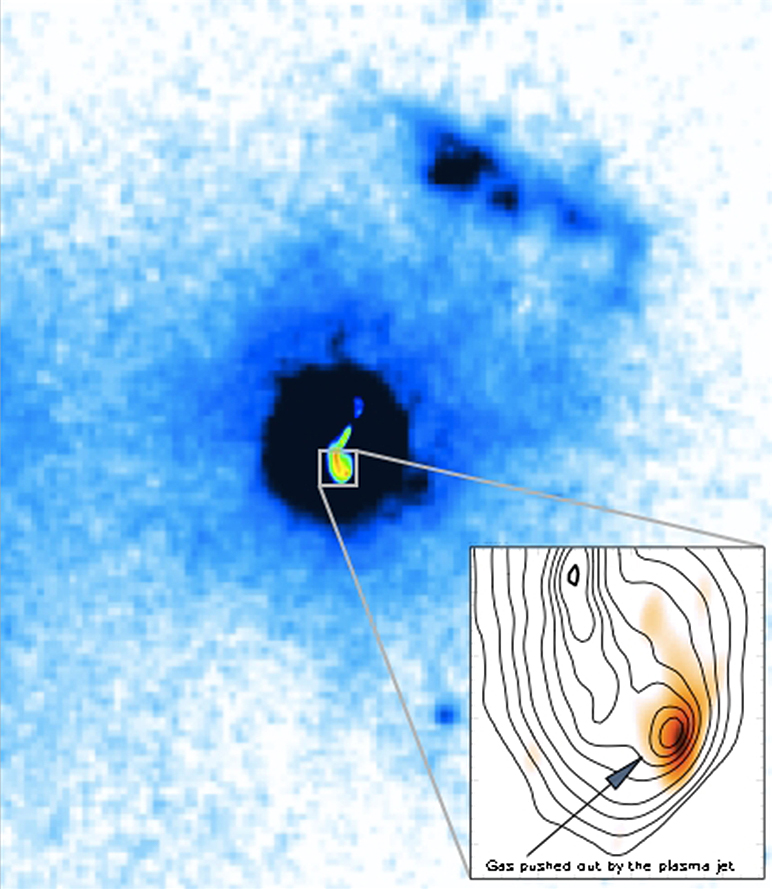
(EUROPA PRESS)
Astrónomos que utilizan una red mundial de radiotelescopios han encontrado pruebas sólidas de que un potente chorro de materia o jet impulsado a la velocidad de la luz por el agujero negro central de la galaxia está soplando grandes cantidades de gas fuera de la galaxia. Este proceso está limitando el crecimiento del agujero negro y la tasa de formación de estrellas en la galaxia, por lo que es una clave para entender cómo se desarrollan las galaxias, según estos científicos.
En los núcleos de las galaxias se han detectado las radiaciones que son propias de la existencia allí de grandes agujeros negros que se tragan toda la materia circundante de gas y polvo e incluso de estrellas vecinas. El espacio a su alrededor se curva y el tiempo se distorsiona.
Existen varias formas teóricamente posibles de agujeros negros.
- Un agujero negro sin rotación ni carga eléctrica (Schwarzschild).
- Un agujero negro sin rotación con carga eléctrica (Reissner-Nordström).
En la práctica es más fácil que los agujeros negros estén rotando y que no tengan carga eléctrica, forma conocida como agujero negro de Kerr. Los agujeros negros no son totalmente negros; la teoría sugiere que pueden emitir energía en forma de radiación Hawking.

La estrella supermasiva, cuando se convierte en un agujero negro se contrae tanto que realmente desaparece de la vista, de ahí su nombre de “agujero negro”. Su enorme densidad genera una fuerza gravitatoria tan descomunal que la velocidad de escape supera a la de la luz, por tal motivo, ni la luz puede escapar de él. En la singularidad, dejan de existir el tiempo y el espacio; podríamos decir que el agujero negro está fuera, apartado de nuestro universo, pero en realidad deja sentir sus efectos ya que, como antes dije, se pueden detectar las radiaciones de rayos X que emite cuando engulle materia de cualquier objeto estelar que se le aproxime más allá del punto límite que se conoce como horizonte de sucesos.
Con la explicación anterior he querido significar que, de acuerdo con la relatividad de Einstein, cabe la posibilidad de que una masa redujera sin límite su tamaño y se autoconfinara en un espacio infinitamente pequeño y que, alrededor de esta, se forme una frontera gravitacional a la que se ha dado el nombre de horizonte de sucesos.
Puesto que el tamaño de un agujero negro depende de la energía absorbida por el mismo, cuanto mayor es la masa del agujero negro, tanto mayor es el radio de Schwarzschild, que viene dada por:
donde:
Una explicación algo más precisa sería: Siguiendo la fórmula de arriba de la imagen: M es la masa del agujero negro, G es la constante gravitacional de Newton, y c2 es la velocidad de la luz elevada al cuadrado. Así, el radio de Schwarzschil para el Sol que tiene un diámetro de 1.392.530 Km, sería de sólo tres kilómetros, mientras que el de la Tierra es de 1 cm: si un cuerpo con la masa de la Tierra se comprimiera hasta el extremo de convertirse en una singularidad, la esfera formada por su horizonte de sucesos tendría el modesto tamaño de una bolita o canica de niños. Por otro lado, para una estrella de unas 10 masas solares el radio de Schwarzschild es de unos 30 kilómetros. Que para nuestro Sol, como he dicho antes, se quedaría en sólo tres kilómetros, tal es su grado de encogimiento sobre sí mismo.
Por otra parte, los acontecimientos que ocurren fuera del horizonte de sucesos en un agujero negro, tienen un comportamiento como cualquier otro objeto cósmico de acuerdo a la masa que presente. Por ejemplo, si nuestro Sol se transformara en un agujero negro, la Tierra seguiría con los mismos patrones orbitales que antes de dicha conversión del Sol en agujero negro.

Ahora bien, y en función de la fórmula anteriormente descrita, el horizonte de sucesos se incrementa en la medida que crece la masa del agujero a medida que atrae masa hacia él y se la traga introduciéndola en la singularidad. Las evidencias observacionales nos invitan a pensar que en muchos centros de galaxias se han formado ya inmensos agujeros negros supermasivos que han acumulado tanta masa (absorciones de materia interestelar y estrellas) que su tamaño másico estaría bordeando el millón de masas solares, pero su radio de Schwarzschil no supera ni las 20 UA (unidad astronómica = 150 millones de Km), mucho menor que nuestro sistema solar.

La singularidad es el pico de abajo que llega a desaparecer de la vista, la densidad adquirida por la materia es tan inmensamente grande que, parece como si hubiera entrado en otro mundo. Sin embargo, su infinita fuerza de gravedad se deja sentir y atrae a todos aquellos objetos que, en las cercanias de sus dominios, osen traspasar el horixonte de sucesos, es decir, la línea de irás y no volverás.
Comprender lo que es una singularidad puede resultar muy difícil para una persona alejada de la ciencia en sí.
Es un asunto bastante complejo el de la singularidad en sí misma, y para los lectores más alejados de los quehaceres de la física, será casi imposible aceptarla. En el pasado, no fue fácil su aceptación, a pesar de las conclusiones radicales que expuso Kart Schwarzschild en su trabajo inspirado en la teoría y ecuaciones de Einstein. De hecho, hasta el mismo Einstein dudó de la existencia de tales monstruos cosmológicos. Incluso durante largo tiempo, la comunidad científica lo consideró como una curiosidad teórica. Tuvieron que transcurrir 50 años de conocimientos experimentales y observaciones astronómicas para empezar a creer, sin ningún atisbo de duda, que los agujeros negros existían realmente.

Sí, es posible que una vez que hayamos representado la singularidad mediante las matemáticas de la relatividad general, la única otra manera de hacerlo sea en el interior de nuestras mentes, imaginando lo que puede ser. Claro que, también la imagen pueda estar refiriéndose a que, nuestras mentes también son singularidades de la materia que han llegado a ser conscientes.
El concepto mismo de “singularidad” desagradaba a la mayoría de los físicos, pues la idea de una densidad infinita se alejaba de toda comprensión. La naturaleza humana está mejor condicionada a percibir situaciones que se caracterizan por su finitud, cosas que podemos medir y pesar, y que están alojadas dentro de unos límites concretos; serán más grande o más pequeñas pero, todo tiene un comienzo y un final pero… infinito, es difícil de digerir. Además, en la singularidad, según resulta de las ecuaciones, ni existe el tiempo ni existe el espacio. Parece que se tratara de otro universo dentro de nuestro universo toda la región afectada por la singularidad que, eso sí, afecta de manera real al entorno donde está situada y además, no es pacífica, ya que se nutre de cuerpos estelares circundantes que atrae y engulle.
La noción de singularidad empezó a adquirir un mayor crédito cuando Robert Oppenheimer, junto a Hartlan S. Snyder, en el año 1.939 escribieron un artículo anexo de otro anterior de Oppenheimer sobre las estrellas de neutrones. En este último artículo, describió de manera magistral la conclusión de que una estrella con masa suficiente podía colapsarse bajo la acción de su propia gravedad hasta alcanzar un punto adimensional; con la demostración de las ecuaciones descritas en dicho artículo, la demostración quedó servida de forma irrefutable que una estrella lo suficientemente grande, llegado su final al consumir todo su combustible de fusión nuclear, continuaría comprimiéndose bajo su propia gravedad, más allá de los estados de enana blanca o de estrella de neutrones, para convertirse en una singularidad.
Un largo recorrido de estrella masiva a Agujero Negro
Estrellas de Neutrones que, con sus campos magnéticos influyen en todo el espacio circundante y, sus pulsos luminosos cuando se dejan ver como púlsares, son como los faros del cielo que avisan a seres de mundos lejanos, que maravillas como esa están ahí.
Los cálculos realizados por Oppenheimer y Snyder para la cantidad de masa que debía tener una estrella para terminar sus días como una singularidad estaban en los límites másicos de M =~ masa solar, estimación que fue corregida posteriormente por otros físicos teóricos que llegaron a la conclusión de que sólo sería posible que una estrella se transformara en singularidad, la que al abandonar su fase de gigante roja retiene una masa residual como menos de 2 – 3 masas solares.
Oppenheimer y Snyder desarrollaron el primer ejemplo explícito de una solución a las ecuaciones de Einstein que describía de manera cierta a un agujero negro, al desarrollar el planteamiento de una nube de polvo colapsante. En su interior, existe una singularidad, pero no es visible desde el exterior, puesto que está rodeada de un horizonte de suceso que no deja que nadie se asome, la vea, y vuelva para contarlo. Lo que traspasa los límites del horizonte de sucesos, ha tomado el camino sin retorno. Su destino irreversible, la singularidad de la que pasará a formar parte.

Alrededor de un agujero negro, y, en objetos cercanos a él, se pueden ver efectos extraordinarios que finalizan con su desaparición dentro del Agujero Negro que, los engulle y cada vez se hace más y más poderoso. Algunos son verdaderos monstruos del Universo y llegan a poseer miles de millones de masas solares. ¿Os imaginais dar un paseo por sus cercanias?
Desde entonces, muchos han sido los físicos que se han especializado profundizando en las matemáticas relativas a los agujeros negros. John Malher (que los bautizó como agujeros negros), Roger Reyrose, Stephen Hawking, Kip S. Thorne, Kerr y muchos otros nombres que ahora no recuerdo, han contribuido de manera muy notable al conocimiento de los agujeros negros, las cuestiones que de ellas se derivan y otras consecuencias de densidad, energía, gravedad, ondas gravitacionales, etc, que son deducidas a partir de estos fenómenos del cosmos.
Se afirma que las singularidades se encuentran rodeadas por un horizonte de sucesos, pero para un observador, en esencia, no puede ver nunca la singularidad desde el exterior. Específicamente implica que hay alguna región incapaz de enviar señales al infinito exterior. La limitación de esta región es el horizonte de sucesos, tras ella se encuentra atrapado el pasado y el infinito nulo futuro. Lo anterior nos hace distinguir que en esta frontera se deberían reunir las características siguientes:
- debe ser una superficie nula donde es pareja, generada por geodésicas nulas;
- contiene una geodésica nula de futuro sin fin, que se origina a partir de cada punto en el que no es pareja, y que
- el área de secciones transversales espaciales jamás pueden disminuir a lo largo del tiempo.
Todo esto ha sido demostrado matemáticamente por Israel, 1.967; Carter, 1.971; Robinson, 1.975; y Hawking, 1.978 con límite futuro asintótico de tal espaciotiempo como el espaciotiempo de Kerr, lo que resulta notable, pues la métrica de Kerr es una hermosa y exacta formulación para las ecuaciones de vacío de Einstein y, como un tema que se relaciona con la entropía en los agujeros negros.

El espacio se distorsiona en presencia de grandes masas. ¿Qué transformaciones no sufrirá en presencia de un Agujero Negro?
No resulta arriesgado afirmar que existen variables en las formas de las singularidades que, según las formuladas por Oppenheimer y su colaborador Snyder, después las de kerr y más tarde otros, todas podrían existir como un mismo objeto que se presenta en distintas formas o maneras.
Ahora bien, para que un ente, un objeto o un observador pueda introducirse dentro de una singularidad como un agujero negro, en cualquiera que fuese su forma, tendría que traspasar el radio de Schwarzschild (las fronteras matemáticas del horizonte de sucesos), cuya velocidad de escape es igual a la de la luz, aunque esta tampoco puede salir de allí una vez atrapada dentro de los límites fronterizos determinados por el radio. Este radio de Schwarzschild puede ser calculado usándose la ecuación para la velocidad de escape


Para el caso de fotones u objeto sin masa, tales como neutrinos, se sustituye la velocidad de escape por la de la luz c2. Para otros objetos mayores como naves espaciales, hay que cumplir los requisitos exigidos por la Ley de la Gravedad que habrá que vencer para escapar del objeto o planeta del que queramos salir.
La velocidad de escape está referida a la velocidad mínima requerida para escapar de un campo gravitacional. El objeto que escapa puede ser cualquier cosa, desde una molécula de gas a una nave espacial. Como antes he reflejado está dada por , donde G es la constante gravitacional, M es la masa del cuerpo y R es la distancia del objeto que escapa del centro del cuerpo del que pretende escapar (del núcleo). Un objeto que se mueva a velocidad menor a la de escape entra en una órbita elíptica; si se mueve a una velocidad exactamente igual a la de escape, sigue una órbita parabólica, y si el objeto supera la velocidad de escape, se mueve en una trayectoria hiperbólica.

Así hemos comprendido que, a mayor masa del cuerpo del que se pretende escapar, mayor será la velocidad que necesitamos para escapar de él. Veamos algunas:
| Objeto | Velocidad de escape |
| La Tierra | ………….11,18 Km/s |
| El Sol | ………….617,3 Km/s |
| Júpiter | ……………59,6 Km/s |
Saturno……………35,6 Km/sVenus………….10,36 Km/sAgujero negro….+ de 299.000 Km/s
Ponernos a comentar sobre objetos y fenómenos que en el Universo están presentes, puede llegar a sar fascinante. A medida que nos sumergimos en las complejidades de las cosas, los procesos mediante los cuáles cambian para convertirse en otras diferentes de las que en un principio eran, los ritmos y energías, las fuerzas fundamentales que actúan sobre ellos…Es una maravilla.
emilio silvera
















 Totales: 83.324.479
Totales: 83.324.479 Conectados: 75
Conectados: 75