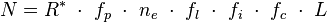Oct
16
¿El primer contacto? ¡Tendrá que esperar!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Vida ~
Clasificado en El Universo y la Vida ~
 Comments (9)
Comments (9)

Todo cambia en el universo, como si de la moda femenina se tratara
En temas científicos controvertidos de los que se tienen pocos datos empíricos, las opciones cambian constantemente, como si de la moda femenina se tratara. La falda se lleva larga durante una década y, ahora cambianmos a la falda corta, muy corta para las más jovencitas y, de esa manera se va de arriba abajo. De la misma manera pasa con los temas científicos cuando no se tienen nociones certeras sobre ellos y, hubo un tiempo en el que se creía que los planetas eran raros en el Universo. Para ello, los cientíicos se basaban en que la Tierra era el fruto de una colisión improbable o un acercamiento excesivo entre dos soles.
Cuando no se sabe, se especula y se emiten teorías que no siempre son las más acertadas. Con toda probabilidad (creían), la vida en el Cosmos estaba supeditada a nuestro Sistema solar, tal vez solamente a la Tierra -cosa que aún hoy, creen algunos “científicos” de pocas luces-. Sin embargo, las opiniones más autorizadas, se han decantado hacia el extremo contrario, es decir, que la vida, prolifera por el Cosmos al igual que los planetas, las estrellas y las galaxias.

Ahora sabemos que los planetas son comunes y su presencia alrededor de las estrellas es de lo más corriente y natural en el proceso de de los astros y los diversos objetos que los orbitan. Los planetas proliferan tanto y son tan comunes que se exhiben a miles de millones -solamente en nuestra propia galaxia- alrededor de sus estrellas rutilantes que les envía luz y calor para que, en aquellos que tengan las precisas condiciones, pueda surgir alguna clase de vida y, en algunos casos, alcanzaran la consciencia como lo hicimos aquí en la Tierra.

Bajo esa hipótesis se inició el Proyecto Ozma y se instaló un poderoso radiotelescopio en Green Bank, Virginia Occidental, apuntando hacia diversos soles de la Galaxia en una búsqueda sistemática de mensajes de radio procedentes e otros mundos. Frank Drake, el radioastrónomo, fue, desde siempre un admirador de L. Frank Baum y sus de Oz. Bautizó el Proyecto con el nombre de Ozma, el soberano de la utopía mítica de Baum. La localización de Oz es desconocida. Sus habitantes son “humanoides”, pero no necesariamente “gente de carne y hueso” como nosotros (como el Leñador de Hojalata y el Espantapájaros), Además Oz está rodeado por el infranqueable Desierto de la Muerte, que destruye a todo aquel que intente tocar un solo grano de su arena.

Siempre hemos imaginados mundos ¿imposible?, o, seguramente intuitivos, toda vez que algo dentro de nuestras mentes nos decía que ahí fuera, podrían estar esos mundos imaginarios. La realidad es a veces mucho más compleja de lo que podamos imaginar. Uno de los personajes de Baum, el Rey Gnomo, tiene un sirviente llamado Oidor Orejudo. Las orejas de este “gnomo” miden metros. Si coloca una de ellas sobre el suelo puede oir sonidos que se producen a miles de kilómetros.
Antes imaginábamos Ciudades Esmeraldas con extraños personajes de comportamientos atípicos y fantásticas criaturas que vivían en un mundo mágico en el que cualquier cosa podría ser cierta y, para nuestro asombro, algunos incluso podían aparecer y desaparecer de nuestra vista como si de duendecillos se tratara. Esos mundos imaginados que están fuera de este y que viven en nuestras mentes, ¿quién sabe?, si en nuestro futuro deambular por esos mundos pedidos por el espacio interestelar, no podremos encontrarnos con alguno de esos extraños mundos en los que existan criaturas que nunca pudimos imaginar.


Las historias que nos contaba Baum, en cierta manera, parecen paradojas de lo que podría ser nuestra realidad de hoy. Aquel desierto que rodeaba el Mundo de Hoz podría ser el Interestelar que nosotros, a pesar de nuestros adelantos, no podemos dominar y la radiación del medio nos puede llevar a la muerte como aquellos granos de arena. Por otra parte, las Orejas descomunales del Oidor Orejudo, son los modernos radiotelescopios que escuchan el sonido de los mundos situados a miles de millones de kilómetros de nosotros.
llevamos muchos años a la espera de captar esas señales codificadas, quizá una repetición de una sencilla secuencia de números, procedente exclusivamente de una fuente inteligente que fuera capaz de comprender las leyes universales de las matemáticas. La posibilidad de oir dicha señal ¡coincide, sin duda, con la del Oziano! Es difícil calcular el asombroso efecto de tal señal en nuestras estructuras mentales, centradas en nosotros mismos y limitadas por los confines de la Tierra.

¿Qué haríamos si recibiéramos una señal de ese tipo? El Chen Ning Yang ha hecho una sugerencia: “!No contestar!” Tal respuesta parece inverosímil. Hace tiempo que matemáticos y lógicos están ocupados en obtener, paso a paso, procedimientos por los cuales los habitantes de dos planetas lejanos pudieran desarrollar lentamente un lenguaje común para poder hablar entre sí. Ya en 1962, el matemártico neerlandés Hans Freudenthal publicó la parte 1 de un ambicioso titulado Lincos: Diseño de un lenguaje para la cópula cósmica.
De todas las maneras, si esos seres inteligentes de otros mundos conocen las leyes fundamentales de la Naturaleza, sin importar que nombres les puedan haber dado, podrían entender pulsaciones codificadas para una comunicación fluida. Una vez establecido el contacto , sería sencillo transmitir dibujos detallados. En su forma más rudimentaria, sería solamente necesario dividir un rectángulo en miles de unidades cuadradas minúsculas, igual que una hoja de papel milimetrado, y trasmitir entonces un código binario, con unos y ceros que indicaran los cuadrados que deben sombrearse (contando los cuadrados de arriba abajo y de izquierda a derecha). Posteriormente, una vez conseguido ese primer mensaje, se podrían transmitir mejores dibujos, incluso, quizá, algunas películas que reflejen la vida terrestre y esperar una corrspondencia igual desde la otra parte.

Claro que, en todo esto hay un fallo que no hemos querido ver hasta el momento: ¡Las inconmensurables distancias! ¿De qué sirve nuestra avanzada tecnología que puede transmitir mensajes a la velocidad de la luz, si resulta que la fuente y el receptor, están separados por decenas de años-luz? En el hipotético caso de que algún día, se reciba esa señal, ese mensaje, ¿cuándo fue enviado? No podemos estar supeditados a un hipotético contacto en el que el mensaje y su respuesta, estén separados por unidades de tiempo que hagan imposible que los que enviaron el mensaje sigan vivos cuando nosotros les podamos contestar.
La única razón por la que no hemos podido contactar todavía con seres inteligentes es esa: ¡La distancia! El Universo es un lugar de distancias que no siempre podemos comprender, y, en nuestra propia Galaxia, la Vía Láctea que tiene 100.000 años-luz de diámetro, existen más de cien mil millones de estrellas que, si están rodeadas de planetas en una media de dos cada estrella… ¿Cuántos planetas existirán? Un inmenso número de mundos están ahí fuera, hemos podido localizar más de mil y, algunos, parecen tener las condiciones precisas para contener en ellos la vida pero, las distancias que nos separan hace imposible que podamos llegar a ellos en un tiempo prudencial que permita ese contacto del que tanto hemos hablado.

Nuestro Sol es sólo una estrella solitaria en la abundancia de 7×1022 estrellas en el universo observable. La Vía Láctea es tan sólo una de entre las 500.000.000.000 galaxias del Universo. Parece que debería haber una gran diversidad de vida ahí fuera. El primero en hacer una estimación inicial fue el astrónomo Frank Drake. Éste concibió una ecuación, ahora conocida como Ecuación de Drake, basada en parámetros:
La ecuación de Drake identifica los factores específicos que, se cree, tienen un papel importante en el desarrollo de las civilizaciones. Aunque en la actualidad no hay suficientes para resolver la ecuación, la comunidad científica ha aceptado su relevancia como primera aproximación teórica al problema, y varios científicos la han utilizado como herramienta para plantear distintas hipótesis.
 es el ritmo anual de estrellas “adecuadas” en la galaxia.
es el ritmo anual de estrellas “adecuadas” en la galaxia. es la fracción de estrellas que tienen planetas en su órbita.
es la fracción de estrellas que tienen planetas en su órbita.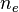 es el número de esos planetas orbitando dentro de la ecosfera de la estrella (las órbitas cuya distancia a la estrella no sea tan próxima como para ser demasiado calientes, ni tan lejana como para ser demasiado frías para poder albergar vida).
es el número de esos planetas orbitando dentro de la ecosfera de la estrella (las órbitas cuya distancia a la estrella no sea tan próxima como para ser demasiado calientes, ni tan lejana como para ser demasiado frías para poder albergar vida).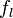 es la fracción de esos planetas dentro de la ecosfera en los que la vida se ha desarrollado.
es la fracción de esos planetas dentro de la ecosfera en los que la vida se ha desarrollado.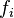 es la fracción de esos planetas en los que la vida inteligente se ha desarrollado.
es la fracción de esos planetas en los que la vida inteligente se ha desarrollado. es la fracción de esos planetas la vida inteligente ha desarrollado una tecnología e intenta comunicarse.
es la fracción de esos planetas la vida inteligente ha desarrollado una tecnología e intenta comunicarse. es el lapso, medido en años, durante el que una civilización inteligente y comunicativa puede existir.
es el lapso, medido en años, durante el que una civilización inteligente y comunicativa puede existir.
(Es obligado decir que, esta especie de fórmula estadística, estaba bien en aquel momento. Sin embargo, hoy se tienen conocimientos más avanzados que nos llevan a una precisión mayor en el tema y a pronosticar con mucha más fiabilidad).

Sabiendo como ahora sabemos, el sin fin de mundos que pueblan las “infinitas” galaxias del Universo, ¿cómo podemos negar la existencia de vida en muchos de esos mundos y que, algunas de esas formas evolucionaran hasta alcanzar la conciencia de Ser? No creo que tengamos argumentos sólidos para poder negar la existencia de vida en muchos de los mundos que son. Otra cuestión es la de poder contactar con ellos, no pocas veces hemos oido decir que “la Naturaleza es sabia”, y no se aparta de mi mente la idea de que es, esa “sabiduría” precisamente, la que hasta el momento ha impedido el encuentro. En la Naturaleza todo tiene un tiempo, las estrellas pueden vivir miles de millones de años que son necesarios para “fabricar” los materiales de la vida, la vida evoluciona en los mundos durante miles de millones de años para poder alcanzar la consciencia, los seres vivos están supeditados a un ciclo de vida limitado en el tiempo y, suplen su efímera existencia, mediante el “truco” de la replicación. De esa manera, se burla la destructiva Entropía y se consigue que la especie perdure.

Para “ellos” las dificultades físicas y tecnológicas son las mismas que para nosotros
No ha llegado el momento de que podamos contactar con seres de otros mundos que, como nosotros, estarán confinados en sus planetas y también, como nosotros, estarán explorando los alrededores de su mundo. El camino seguido por otras clases de vida debe ser muy similar al que se ha dado aquí en la Tierra, los procesos habrán muy similares y, siendo posible que puedan existir algunas civilizaciones algo más avanzadas que la nuestra, no es probable que tengan la posibilidad de llegar hasta nosotros, porque de ser así… ¿Dónde están?
¿El primer contacto ? ¡Tendrá que esperar!
“La astrofísica Jocelyn Bell Burnell realizó unas sorprendentes declaraciones en la conferencia de Euroscience Open Fórum en Dublín, la humanidad tendrá un contacto con seres extraterrestres, y sugirió que los gobiernos se deben preparar ante tal situación.“Sospecho que próximamente recibiremos señales de vida de otros mundos, muy posiblemente de vida inteligente, antes del próximo siglo. ¿Estamos bien preparados? ¿Sabemos como vamos ha realizar el contacto con ellos? ¿Los pondremos en un parque zoológico, nos los comeremos, o enviaremos a los soldados para hacerles saber lo que es la democracia?”
La predicción científica la realizó delante de los mejores científicos, además añadió que la vida extraterrestre podría encontrarse en planetas rocosos con atmósferas de dióxido de carbono o con capas de ozono. Pero también reconoció que actualmente es difícil comunicarse con “ellos”, ya que nada puede viajar más rápido que la velocidad de la luz. Así que una comunicación estelar no seria posible hasta dentro de 50 o 100 años.”
Está claro que los términos empleados por Jocelyn Bel no fueron muy afortunados, dado que, si son “ellos” los primeros en hacer ese contacto, es que han logrado algo que nosotros no hemos podido conseguir, es decir, serían más inteligentes que nosotros y, “meterlos en un zoo…” ¡No parece probable.
emilio silvera
Oct
16
¡Cuántas maravillas! Y, nuestra Mente, entre ellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Parafraseando a Hilbert: ¡Tenemos que saber, y sabremos!
En la tumba de David Hilbert (1862-1943), en el cementerio de Gotinga (Alemania), dice:
“Debemos saber. Sabremos”.
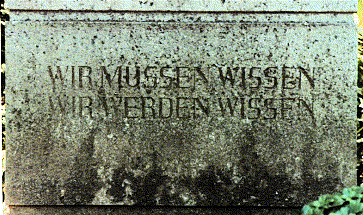
Hilbert nos hacía su planteamiento que era obtener la respuesta a tres importantes preguntas:
- ¿Son las matemáticas completas, es decir cualquier proposición puede ser probada o rechazada?
- ¿Son las matemáticas consistentes, es decir, no es posible demostrar algo falso?
- ¿Son las matemáticas decidibles, es decir, cualquier proposición se puede demostrar como cierta o falsa tras una secuencia finita de pasos?”


La importancia de la Simetría en la Naturaleza



No sería descabellado decir que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría decadimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia. Por ejemplo, la fuerza de Gravedad generada por la presencia de la materia, determina la geometría del espacio-tiempo.
Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física. De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.

Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

Geometría → teoría de campos → teoría clásica → teoría cuántica.
Contrariamente, la teoría de supercuerdas ha estado evolucionando hacia atrás su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.
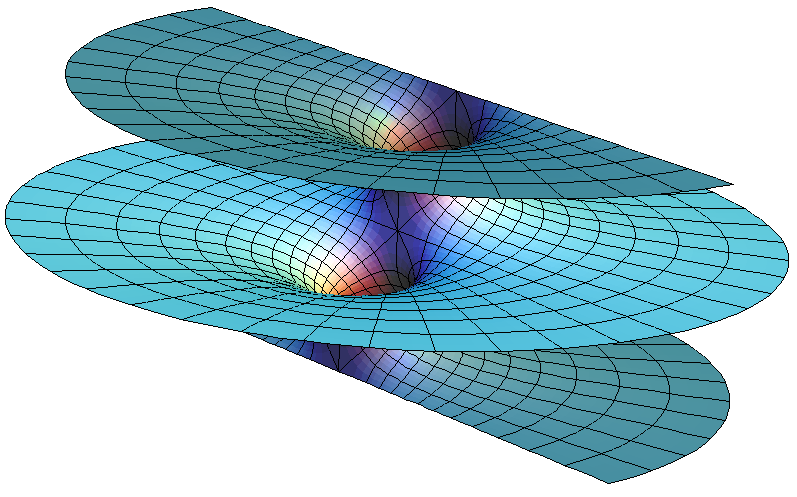
La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.
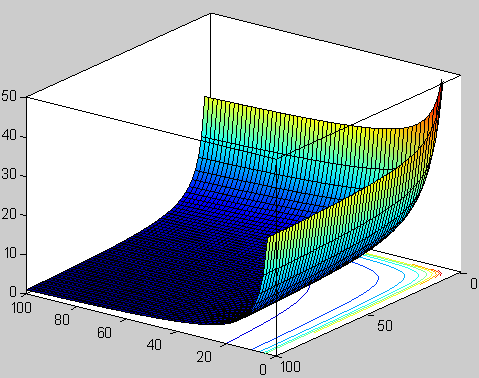
Función beta. Representación de la función valores reales positivos de x e y.
Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de , prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.
Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.


Gabriele Veneziano es un físico italiano Mahiko Suzuki
En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, como la teoría de cuerdas fue descubierta atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades. El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.
Así, Witten dice:
“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos c del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos ahora mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”
Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.
Ni con colección de llaves podremos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la Teoría M, la más moderna versión de la cuerdas expuesta por E. Witten y que, según contaron los que estuvieron presentes en su presentación, Witten les introdujo en un “universo” fascinante de inmensa belleza que, sin embargo, no puede ser verificado por el experimento.
El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.

¿Por qué diez dimensiones?
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.
Al manipular los diagramas de lazos1 de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

Cuando nos asomamos a la Teoría de cuerdas, entramos en un “mundo” lleno de sombras en los que podemos ver brillar, a lo lejos, un resplandor cegador. Todos los físicos coinciden en el hecho de que es una teoría muy prometedora y de la que parece se podrán obtener buenos rendimientos en el futuro pero, de , es imposible verificarla.
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. extraña función contiene un término elevado a la potencia veinticuatro.

La magia esconde una realidad
El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

“En matemática, la función theta de Ramanujan generaliza la forma de las funciones theta de Jacobi, a la vez que conserva sus propiedades generales. En particular, el producto triple de Jacobi se puede escribir elegantemente en términos de la función theta de Ramanujan. La función toma nombre de Srinivasa Ramanujan, y fue su última gran contribución a las matemáticas.”
Como un revoltijo de hilos entrecruzados que son difíciles de seguir, así son las matemáticas de la teoría de cuerdas
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Godfrey Harold Hardy
G. H. Hardy, el mentor de Ramanujan, trató de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló:
“Parecía ridículo importunarle sobre como había descubierto o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Ramanujan
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y la suma de 9 x 9 x 9 y 10 x 10 x 10).
Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Fórmula de Ramanujan determinar los decimales de pi
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Nuestro mundo asimétrico hermosas simetrias
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de cuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

Volviendo a Ramanujan…
Es innegable lo sorprendente de su historia, un muchacho pobre con escasa preparación y arraigado como pocos a sus creencias y tradiciones, es considerado como una de los mayores genios de las matemáticas del siglo XX. Su legado a la teoría de números, a la teoría de las funciones theta y a las series hipergeométricas, además de ser invaluable aún sigue estudiándose por muchos prominentes matemáticos de todo el mundo. Una de sus fórmulas más famosas es la que aparece más arriba en el lugar número 21 de las imágenes expuestas y utilizada para realizar aproximaciones del Pi con más de dos millones de cifras decimales. Otra de las sorprendentes fórmulas descubiertas por Ramanujan es un igualdad en que era “casi” un número entero (la diferencia era de milmillonésimas). De hecho, durante un tiempo se llegó a sospechar que el número era efectivamente entero. No lo es, pero este hallazgo sirvió de base la teoría de los “Cuasi enteros”. A veces nos tenemos que sorprender al comprobar hasta donde puede llegar la mente humana que, prácticamente de “la nada”, es capaz de sondear los misterios de la Naturaleza para dejarlos al descubierto ante nuestros asombros ojos que, se abren como platos ante tales maravillas.
Publica: emilio silvera
”Algunas personas buscan un significado a la vida a través del beneficio, a través de las relaciones personales, o a través de experiencias propias. Sin embargo, creo que el estar bendecido con el intelecto para adivinar los últimos secretos de la naturaleza da significado suficiente a la vida”.















 Totales: 75.604.220
Totales: 75.604.220 Conectados: 66
Conectados: 66