Oct
11
¿Que es el principio de exclusión de Pauli?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (2)
Comments (2)

El principio de exclusión de Pauli es un principio cuántico enunciado por Wolfgang Ernst Pauli en 1925. Establece que no puede haber dos fermiones con todos sus números cuánticos idénticos (esto es, en el mismo estado cuántico de partícula individual) en el mismo sistema cuántico ligado.1 Formulado inicialmente como principio, posteriormente se comprobó que era derivable de supuestos más generales: de hecho, es una consecuencia del teorema de la estadística del spin.
Debido al principio de exclusión de Pauli, es imposible que dos fermiones ocupen el mismo cuántico (al contrario de lo que ocurre con los bosones). La condensación Bose-Einstein es de importancia fundamental para explicar el fenómeno de la superfluidez. A temperaturas muy bajas (del orden de 2×10-7 K) se puede formar un condensado de Bose-Einstein, en el que varios miles de átomos dorman una única entidad (un superátomo). Este efecto ha sido observado con átomos de rubidio y litio.

Condensado de Bose-Einstein
Como ha habréis podido suponer, la condensación Bose-Einstein es llamada así en honor al físico Satyendra Nath Bose (1.894 – 1.974) y a Albert Einstein. Así que, el principio de exclusión de Pauli tiene aplicación no sólo a los electrones, sino también a los fermiones; pero no a los bosones.
Las reglas de la mecánica cuántica tienen que ser aplicadas si queremos describir estadísticamente un sistema de partículas que obedece a reglas de ésta teoría en vez de las de la mecánica clásica. En estadística cuantica, los estados de energía se considera que están cuantizados. La estadística de Bose-Einstein se aplica si cualquier de partículas puede ocupar un estado cuántico dado. Dichas partículas (como dije antes) son los bosones que, tienden a juntarse.
Los bosones tienen un momento angular n h / 2p, donde n es cero o un entero y h es la constante de Planck. bosones idénticos, la función de ondas es siempre simétrica. Si solo una partícula puede ocupar un cuántico, tenemos que aplicar la estadística Fermi-Dirac y las partículas (como también antes dije) son los fermiones que tienen momento angular (n+½) h/2p y cualquier función de ondas de fermiones idénticos es siempre antisimétrica.
La mejor teoría para explicar el mundo subatómico nació en 1928 cuando el teórico Paul Dirac combinó la mecánica cuántica con la relatividad especial para explicar el comportamiento del electrón. El resultado fue la mecánica cuántica relativista, que se transformó en un ingrediente primario en la teoría cuántica de campos. Con unas pocas suposiciones y unos ajustes ad-hoc, la teoría cuántica de campos ha probado ser suficientemente poderosa para formar la base del modelo estándar de las partículas y las fuerzas.


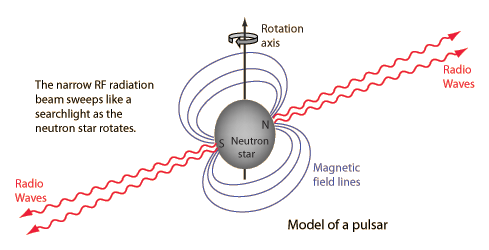
El campo magnético de las estrellas de neutrones
Si nos fijamos en todo lo que estamos hablando aquí, es fácil comprender cómo un campo magnético la partícula cargada que gira, pero ya no resulta tan fácil saber por qué ha de hacer lo mismo un neutrón descargado. Lo cierto es que cuando un rayo de neutrones incide sobre un hierro magnetizado, no se comporta de la misma que lo haría si el hierro no estuviese magnetizado. El magnetismo delneutrón sigue siendo un misterio; los físicos sospechan que contiene cargas positivas y negativas equivalente a cero, aunque por alguna razón desconocida, logran crear un campo magnético cuando gira la partícula.
Particularmente creo que, si el neutrón tiene masa, si la masa es energía (E = mc2), y si la energía es electricidad y magnetismo (según Maxwell), el magnetismo del neutrón no es tan extraño, sino que es un aspecto de lo que en realidad es materia. La materia es la luz, la energía, el magnetismo, en definitiva, la fuerza que reina en el universo y que está presente de una u otra forma en todas partes (aunque no podamos verla).
Sea fuere, la rotación del neutrón nos da la respuesta a esas preguntas:
¿Qué es el antineutrón? Pues, simplemente, un neutrón cuyo movimiento rotatorio se ha invertido; su polo sur magnético, por decirlo así, está arriba y no abajo. En realidad, el protón y el antiprotón, el electrón y el positrón, muestran exactamente el mismo fenómeno de los polos invertidos.
Es indudable que las antipartículas pueden combinarse formar la antimateria, de la misma que las partículas corrientes forman la materia ordinaria.
La primera demostración efectiva de antimateria se tuvo en Brookhaven en 1.965, donde fue bombardeado un blanco de berilio con 7 protones BeV y se produjeron combinaciones de antiprotones y antineutrones, o sea, un antideuterón. entonces se ha producido el antihelio 3, y no cabe duda de que se podría crear otros antinúcleos más complicados aún si se abordara el problema con más interés.

Pero, ¿existe en realidad la antimateria? ¿Hay masas de antimateria en el universo? Si las hubiera, no revelarían su presencia a cierta distancia. Sus efectos gravitatorios y la luz que produjeran serían idénticos a los de la materia corriente. Sin embargo, cuando se encontrasen las masas de las distintas materias, deberían ser claramente perceptibles las reacciones masivas del aniquilamiento mutuo resultante del encuentro. Así pues, los astrónomos observan especulativamente las galaxias, tratar de encontrar alguna actividad inusual que delate interacciones materia-antimateria.
La verdad es que, el momento, el éxito ha sido nulo y la antimateria, si existió alguna vez, quedó destruída en esos primeros momentos del Big Bang y, desapareció debido a que, la materia bariónica era algo mayor que la antimateria, es decir, había más protones que antiprotones.

Los físicos hablan de antipartícula y se están refiriendo a una partícula subatómica que tiene la misma masa que otra partícula y valores iguales pero opuestos de otra propiedad o propiedades. Por ejemplo, la antipartícula del electrón es el positrón, que tiene una carga positiva igual en módulo a la carga negativa del electrón. El antiprotón tiene una carga negativa igual al módulo de la carga positiva del protón. El neutrón y el antineutrón tienen momentos magnéticos con signos opuestos en relación con sus espines. La existencia de antipartículas es predicha por la mecánica cuántica relativista.
Cuando una partícula y su antipartícula colisionan ocurre la aniquilación. La antimateria consiste en materia hecha de antipartículas. Por ejemplo, el antihidrógeno consiste en un antiprotón con un positrón orbitando. El antihidrógeno ha sido creado artificialmente en laboratorio. El espectro del antihidrógeno debería ser idéntico al del hidrógeno y, precisamente por eso, es tan difícil para los astrónomos localizar antimateria (si es que la hay).

Parece que el Universo está formado mayoritariamente de materia (ordinaria) y la explicación de la ausencia de grandes cantidades de antimateria debe ser incorporada en modelos cosmológicos que requieren el uso de teorías de gran unificación de las partículas elementales.
Y, a todo esto, no debemos olvidarnos de la otra materia, esa que llamamos oscura y que, en realidad, deja al descubierto nuestra inmensa ignorancia, ya que, todo el Universo está empapado de ella, y, sin embargo, aún no hemos sido capaces de discernir lo que dicha materia oscura pueda ser, como se formó, o de qué está hecha y cómo se generó en el Universo, en verdad es un gran misterio qur todos los Astrónomos del mundo persiguen incansables.
Ahora se habla de otras dimensiones, y, nuestro cerebro está conformado en tres espaciales y una temporal ( la relatividad especial) y, desde luego, nos cuesta “ver” dimensiones más altas y no podemops crear en nuestras mentes imágenes que nos lleven a 5, 10, 11 o cualquier de dimensiones que están fuera de nuestro alcance mental pero, las matemáticas nos dicen que podrían muy bien existir y, para ello, han ideado una hermosa Teoría del Todo que llaman de supercuerdas o Teoría M.

Por mucho que esforzamos nuestra imaginación, visualizar esas dimensiones extra… ¡No será nada fácil! Nuestro muntro es tridimensional más el Tiempo que, desde Einstein, es la cuarta dimensión, Sin embargo, aunque con la numerología se trabaja con más dimensiones, y, los físicos de cuerdas logran que la Cuántica y la Relatividad (lo pequeño y lño grande) se junten sin alborotos, en la realidad cotidiana, donde las matemáticas quedan fuera, esas dimensiones más altas… ¡No se ven por ninguna parte!
Según los físicos, si es verdad que dichas dimensiones están ahí, ¿no podría esa materia y energía oscura estar alojada en alguna de ellas? Tengo un registrado en la Sociedad de Autores científicos que, precisamente se refiere a eso, a que la materia oscura pueda estar fuera de nuestra visión y que no la podamos detectar precisamente por no tenerla a la vista, y, mediante fluctuaciones del vacío, esa cantidad ingente de materia oscura deja pasar a los gravitones, los bosones intermediarios de la fuerza de Gravedad, que llegan a nuestro propio espacio, a nuestras dimensiones, y, se deja sentir haciendo que las galaxias se alejen las unas de las otras a mayor velociodad de lo que lo harían si la única materia presente fuese la Bariónica.
En fin, amigos, es tanto lo que no sabemos que, mejor será la búsqueda de éste y de otros misterios que, como el de la masa de las partículas, aún se nos escapa y tenemos que construir maravillas como el LHC para tratar de que responda a nuestras preguntas.

Una máquina gigantesca que quiere viajar hasta las cuerdas vibrantes
Pero, una cosa es cierta, nuestra osadía que nos lleva a comentar sobre cosas que no llegamos a comprender y, como por ejemplo, los taquiones, son simplemente objetos creados en nuestra inagotable imaginación. Los taquiones, si lo recordais, son partículas hipotéticas que viajan a mayor velocidad que la de la luz y, según la teoría electromagnética, una partícula cargada que viaja a través de un medio con velocidad mayor que la de la luz en ese medio emite radiación Cerenkov y, un taquión cargado emitirá radiación Cerenkov incluso en el vacío.
Claro que, por el momento no se han detectado partículas con esas caracterísiticas y, si llegan a hacer acto de presencia, ¿qué hacemos con la relatividad especial de Einstein que nos dice que nada en nuestro Universo podrá ir a más velocidad que la luz?
¡Es un serio problema! Mejor que el dichoso Taquión no aparezca.

Por otra parte, nunca podremos dejar de sorprendernos cuando nos sumergimos en el “universo” de la mecánica cuántica y en el mundo subatómico de las partículas. El 18 abril 2012, investigadores del Instituto Kavli de TU Delft y de la Fundación FOM han logrado una primera detección de partículas Majorana. Etore Majorana fue un brillante físico italiano que llevó a cabo sus investigaciones en los años treinta del siglo pasado, ahondando en la teoría cuántica y como una partícula especial que podría existir, una partícula que sería en sí misma su propia antipartícula: el fermion de Majorana. Eso sitúa a partícula en la frontera entre materia y antimateria.
¿Será cierto aquello de que, todo lo que podamos imaginar se puede convertir en realidad… ¡con el paso del tiempo!
emilio silvera
Oct
11
¡La Física! Siempre nos sorprende
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

 Diagrama de un microscopio de fuerza atómica
Diagrama de un microscopio de fuerza atómica
Las veloces computadoras cuánticas hechas con átomos atrapados por haces de luz pueden estar un poco más cerca, gracias a las primeras imágenes de átomos individuales obtenidas en una de estas grillas.
La velocidad de las computadoras cuánticas tiene que ver con el hecho de que sus componentes pueden ocupar una serie de estados en lugar de sólo dos como ocurre en una computadora binaria. Ciertos algoritmos especiales podrían explotar estos estados cuánticos para resolver problemas que derrotarían a una computadora convencional.
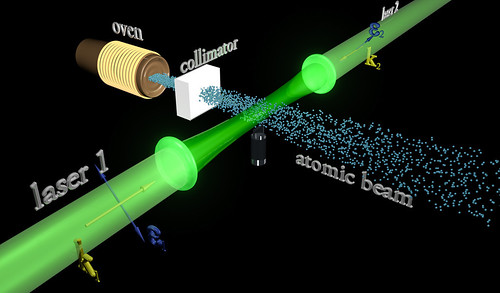
Una candidata a computadora de este tipo es la llamada “rejilla óptica”, en la que haces de rayos láser estratégicamente ubicados hacen que los átomos ultrafríos se coloquen en forma de grilla, como si fueran huevos en su envase de cartón. Pero antes de que uno pudiera leer o escribir sobre estos átomos, algo indispensable si la rejilla fuera a actuar como una computadora cuántica, haría falta determinar las posiciones exactas de los mismos.
Ahora dos equipos de investigadores, uno conducido por Stefan Kuhr del Instituto Max Planck de Óptica Cuántica de Garching, Alemania, y el otro por Markus Greiner de la Universidad de Harvard, han dado el primer paso al obtener imágenes de átomos individuales de rubidio en una rejilla óptica. Este es un reto no sólo porque los átomos son pequeños, sino también porque los fotones de los átomos cercanos pueden interferir unos con otros, enturbiando cualquier patrón.

Para superar esto, los equipos estudiaron el patrón de luz de un solo átomo. Luego crearon un algoritmo capaz de generar una combinación de este patrón a partir de diferentes disposiciones de una grilla de átomos. Cotejando estas simulaciones con el modelo real observado, el algoritmo podía determinar cuál era la distribución de los átomos.
Cada átomo en la grilla actúa como un bit cuántico. Kuhr dice que la rejilla óptica tiene muchos más de estos “qubits” que otros sistemas enfocados en la computación cuántica, por lo que puede ofrecer mayor velocidad.


Los láseres pueden volver reales las partículas virtuales. Los láseres de última generación tienen el poder de crear materia por medio de la captura de partículas fantasmales que, de acuerdo a la mecánica cuántica, permean el espacio aparentemente vacío
El principio de incertidumbre de la mecánica cuántica implica que el espacio nunca puede estar realmente vacío. En cambio, las fluctuaciones aleatorias causan el nacimiento de un caldero hirviente de partículas, como electrones y sus homólogos de antimateria, los positrones.
Las llamadas “partículas virtuales” normalmente se aniquilan entre sí demasiado rápido para que las veamos. Pero los físicos predijeron en los años 30 que un campo eléctrico muy fuerte transformaría las partículas virtuales en reales, y entonces las podríamos observar. El campo las impulsa en direcciones opuestas, porque tienen cargas eléctricas que se oponen, y las separándolos de modo que no puede destruirse mutuamente.


Los láseres son ideales para esta tarea, porque su luz posee campos eléctricos fuertes. En 1997, los físicos del Stanford Linear Accelerator Center (SLAC), en Menlo Park, California, utilizaron luz láser para crear unas pocas parejas de electrón-positrón. Ahora, nuevos cálculos indican que los láser de nueva generación serán capaces de crear pares por millones.
Reacción en cadena
En el experimento de SLAC, sólo se creó un par electrón-positrón a la vez. Pero con los láseres más potentes, es probable que se produzca una reacción en cadena.
El primer par es acelerado a gran velocidad por el láser, haciendo que emita luz. Esta luz, junto con la del láser, genera aún más pares, dice Alexander Fedotov de la Dirección Nacional de Investigaciones Nucleares de la Universidad de Moscú y sus colegas en un estudio que aparecerá en Physical Review Letters.
“Surgirá una gran cantidad de partículas del vacío”, dice John Kirk del Instituto Max Planck de Física Nuclear en Heidelberg, Alemania, que no participó en el estudio.
En los láseres que pueden concentrar cerca de 1026 vatios en un centímetro cuadrado, esta reacción desatada debería convertir de manera eficiente la luz del láser en millones de pares de electrones positrones, calcula el equipo.
Fábrica de antimateria

Ese nivel de intensidad lo podría alcanzar un láser que será construido por el proyecto Extreme Light Infrastructure en Europa. La primera versión del láser se podría construir en 2015, pero podría llevar un año más completar las actualizaciones necesarias para llegar a 1026 vatios por centímetro cuadrado, dice el coautor del estudio Georg Korn del Instituto Max Planck de Óptica Cuántica en Garching , Alemania.
La capacidad de generar una gran cantidad de positrones podría ser útil para los colisionadores de partículas, como el propuesto del Colisionador Lineal Internacional, que impactará electrones y positrones, dice Kirk McDonald de la Universidad de Princeton en Nueva Jersey.
Pero Pisin Chen, de la Universidad Nacional de Taiwan en Taipei, dice que el costo de los poderosos láseres puede hacer que este método sea más caro que el alternativo. En la actualidad, la manera estándar de crear una gran cantidad de positrones es disparar un haz de electrones de alta energía a una pieza de metal, para producir pares electrón-positrón. Vean la publicación siguiente:
La materia supera a la antimateria en un experimento que imita a la creación

El desequilibrio en el acelerador de partículas de Illinois podría presagiar grandes avances en Física
A menos de una billonésima de segundo después del Big Bang ocurrió otro evento tumultuoso. Aunque el Cosmos nació con partes iguales de materia y antimateria, que se destruyeron una a la otra al entrar en contacto, de alguna forma la materia comenzó a predominar. Los físicos han descubierto una nueva pista sobre la causa de este desequilibrio fortuito, que condujo a la existencia de galaxias, planetas y personas.

Circunferencia de 4 kilómetros de diámetro del Acelerador de Partículas del Laboratorio Fermi de Chicago
El nuevo hallazgo se basa en ocho años de estudio de la desintegración de partículas de vida corta, llamadas mesones B, que se produce durante las colisiones de alta energía en el acelerador de partículas Tevatrón del Laboratorio Fermi (Fermilab), ubicado en Batavia, Illinois. Los científicos del experimento DZero del Tevatrón han descubierto que los mesones B, cuando se desintegran, producen cerca del 1 % más de pares de muones (una versión pesada del electrón) que de pares de sus antipartículas, los antimuones. Los físicos se refieren a este fenómeno como una violación CP.
El desequilibrio, reportado el 14 de mayo en un seminario del Fermilab y publicado en Internet el 18 de mayo, podría servir para entender cómo fue que la materia superó a la antimateria en el Universo. También aumenta las posibilidades de que el Gran Colisionador de Hadrones, el acelerador de Suiza que sustituyó al Tevatrón como el colisionador de partículas más poderoso del mundo, encuentre nuevas partículas elementales o una nueva física. Hablamos del LHC que, de hecho, las ha encontrado.

El acelerador de partículas Tevatróndel Laboratorio Fermi (Fermilab),ubicado en Batavia, Illinois. Fue el primero en producir antimateria
“Aunque pequeño, este excedente del 1% es 50 veces más grande que la asimetría entre materia y antimateria prevista para la desintegración de mesones B por el modelo estándar de la Física de Partículas”, señala el portavoz del DZero, Stefan Söldner-Rembold, de la Universidad de Manchester en Inglaterra.
“Se nos puso la piel de gallina”, cuenta Söldner-Rembold acerca del momento en el que él y los 500 colaboradores del DZero comprendieron lo que habían descubierto. “Estábamos muy contentos porque significa que hay una nueva Física más allá del modelo estándar que tiene que estar a nuestro alcance para que la asimetría sea tan grande”.
“Aunque hay una probabilidad de menos del 0,1 % de que los resultados del DZero sean una casualidad, de acuerdo con las normas de la Física de Partículas hay que considerarlos como indicios aún por confirmar”, advierte el teórico Yuval Grossman de la Universidad de Cornell. Söldner-Rembold señala que los hallazgos del DZero son similares a una asimetría en la producción de materia-antimateria descubierta hace un año por otro experimento llevado a cabo en el Tevatrón, el CDF, pero los nuevos resultados tienen una precisión mayor.”
“Las teorías que podrían explicar las observaciones del DZero incluyen la supersimetría, que supone que cada partícula elemental en el modelo estándar de la Física de Partículas tiene una superpareja más pesada todavía por descubrir”, explica la teórica del Fermilab Marcela Carena, que no pertenece al equipo descubridor. “Otras teorías posibles incluyen un modelo en el que la gravedad y otras fuerzas operan en otras dimensiones ocultas, y la noción de que hay una cuarta familia de quarks más allá de las tres generaciones (arriba y abajo, encanto y extraño, y cima y fondo) que sirven como bloques de construcción de los núcleos atómicos y otras partículas.
“En los modelos que consideran una cuarta familia de quarks, la presencia de quarks nuevos y pesados y su interacción con las tres familias conocidas podrían dar lugar a un desequilibrio mayor entre materia y antimateria que el que se encuentra en el modelo estándar”, señala Carena. Y agrega: “En la teoría de la supersimetría, las superparejas pesadas jugarían un rol similar al de los quarks pesados, creando interacciones que podrían favorecer la producción de materia sobre la antimateria”.
No siempre la física lo puede explicar todo. Sin embargo… ¡Lo va consiguiendo!
En la teoría de las dimensiones extra, nuevas partículas mensajeras (portadoras de fuerzas previamente desconocidas) se moverían en dimensiones ocultas. Estas partículas transportadoras podrían alterar la carga y otra propiedad, llamada “sabor”, de las partículas elementales, causando el desequilibrio adicional entre materia y antimateria.
Carena añade: “Sin embargo, es difícil encontrar una teoría que pueda explicar esta asimetría sin contradecir otros resultados experimentales”.

La materia superó a la antimateria en el comienzo
Ulrich Nierste, de la Universidad de Karlsruhe en Alemania, advierte: “La conexión del resultado del DZero con el excedente de materia que existe en el Universo es vaga. Si bien el hallazgo insinúa una nueva fuente de asimetría en las propiedades del mesón B y de su antipartícula, el proceso que creó más partículas que antipartículas en el Universo primitivo podría involucrar un mecanismo físico muy diferente”.
“Sin embargo”, dice Carena, “hace falta alguna nueva fuente de asimetría para explicar el desequilibrio que hay entre la materia y la antimateria en el Universo, y, por lo tanto, nuestra existencia”. En cualquiera de los modelos propuestos “el Gran Colisionador de Hadrones debería ser la ventana directa para observar nuevas partículas”.
Uno de los experimentos más pequeños del Colisionador, diseñado para estudiar los mesones B, podría confirmar los hallazgos del DZero dentro de uno o dos años”, dice Yuval Grossman. Y agrega: “Los experimentos más grandes podrían entonces buscar nuevas partículas que serían el origen del desequilibrio cósmico entre materia y antimateria y determinar sus masas”.

El experimento Beauty (Belleza) es la matriz de investigación para la creación de antimateria. El choque de dos protones contra otro a la velocidad de la luz, ha tenido como resultado una partícula con 5 veces más masa que sus protones originales. A esa exótica partícula se le ha llamado B+ y está compuesta por un quark b-anti y un quark u. La partícula B+ se desintegra a una altísima velocidad pero le da tiempo a recorrer ¡¡2 mm!! antes de desintegrarse en dos partículas, el mesón J / ? y el Kaon K+. Esta distancia, comparada con los minúsculos tamaños que estamos tratando, es una auténtica pasada. Hemos tenido antimateria pura moviéndose a lo largo de dos extensos milímetros de “nuestro” espacio. Impresionante.
Lo revolucionario sin embargo es que de esta forma, los investigadores habrían demostrado la teoría de Albert Einstein. “Sí, podemos crear masa a partir de energía usando la famosa fórmula de Einstein, E=mc2, dicen los responsables del CERN. Aunque también hay que destacar que la confirmación de que existe la antimateria plantea muchas preguntas de difícil resolución puesto que esa sustancia no existe en nuestro universo. “Ya que la desaparición de antimateria primordial no puede ser explicada por el modelo tradicional, tendremos que comenzar a pensar en algo nuevo”, afirman los investigadores. “Los científicos están evaluando diferentes posibilidades pero, dado que sólo podemos observar un 4% de la energía y materia total del universo, podemos inferir que la respuesta al misterio de la antimateria se encuentra en la parte desconocida del mismo”, concluyen.


Como podéis ver, las preguntas son muchas y, las respuestas, son más escasas. Sin embargo, no dejamos de insistir y buscar con todos medios a nuestro alcance para saber sobre la Naturaleza no ya de la materia y la antimateria, sino sobre los muchos enigmas que tenemos planteados y a los que no sabemos dar una adecuada explicación. Parece que a lo lejos vemos una luz cegadora que nos inyecta la esperanza necesaria para seguir la búsqueda y tratar de llegar al corazón de todos esos secretos que el Universo esconde.
Hay cosas que… más que sorprendentes son… ¡Inclreibles! He leído por ahí que…
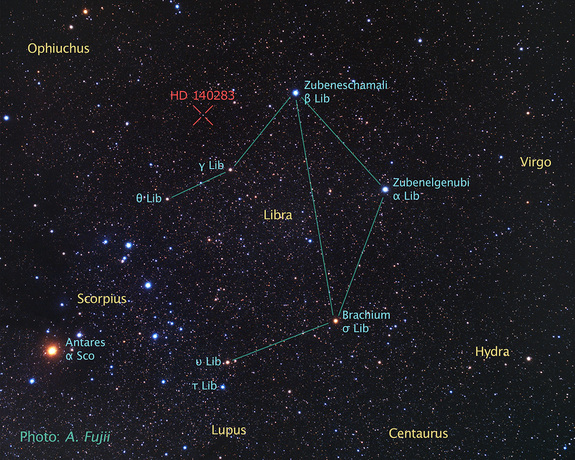
“Un grupo de astrónomos, usando datos del telescopio espacial Hubble, ha determinado la edad de la que es la estrella más vieja cuya edad puede medirse con precisión. El resultado ha sido que la edad de la estrella es de 14.500 ± 800 millones de años, mayor que la estimación de la edad del universo, unos 13.800 millones de años. La estrella en cuestión (HD 140283), también llamada “estrella Matusalén,” una gigante roja que se encuentra a una distancia de 190,1 años luz en la constelación de Libra (distancia medida con precisión mediante la técnica de paralaje). En el año 2000 se dató su edad en 16.000 millones de años. Sin embargo, existen algunas cuestiones que podrían aclarar la extrema edad de esta estrella. Nuevos modelos sobre la difusión de helio en el núcleo indican que la penetración del mismo podría ser mayor de la que se piensa, lo que provocaría un menor ritmo de combustión. También la relación oxígeno-hierro en esta estrella es anómala, demasiado grande, por lo que se cree que futuras observaciones que puedan determinar con mayor grado de precisión la abundancia de oxígeno podrían reducir nuevamente la estimación de la edad de la estrella.”

Oct
11
Racionalizar las cosas, asegurar decisiones
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Curiosidades ~
Clasificado en Curiosidades ~
 Comments (0)
Comments (0)

¿Os acordais de la Mars Climater Orbiter? Allá por el mes de Septiembre de 1998, la NASA preparaba a bombo y platillo la gran noticia que sacudiría el “mundo” de Prensa con una gran noticia. En breve (dijeron), saldría para el planeta Marte la nueva misión comocida como la Mars Climater Orbiter, diseñada para estudiar la atmósfera superior de Marte y, estaba acondicionada para poder enviarnos importantes sobre el clima y la atmósfera marciana. En lugar de ello, simplemente se estrelló contra la superficie marciana.
La distancia entre la nave espacial y la superficie del planeta Marte era de 96,6 kilómetros inferior de lo que pensaban los controladores de la misión, y 125 millones de dolares desaparecieron en el rojo polvo de la superficie de Marte. La pérdida ya era suficientemente desastrosa, pero aún, hubo que morder más el polvo cuando se descubrió la causa: Lockheed-Martin, la empresa que controlaba el funcionamiento diario de la nave espacial, estaba enviando datos al control de la misión en unidades imperiales -millas, pies y libras de fuerza- mientras que el equipo de investigación de la NASA estaba suponiendo, como el resto del mundo científico internacional, que recibián las instrucciones en unidades métricas. La diferencia entre millas y kilómetros fue lo suficiente para desviar la nave unas 60 millas el curso previsto y llevarla a una órbita suicida hacia la suprficie marciana, en la que quedó chafada e inservible dando al traste, no ya con (que también) sino con un montón de ilusionados componentes del equipo que esperaban grandes acontecimientos del Proyecto.

La lección que podemos obtener de catástrofe está muy clara: ¡Las Unidades de medida son importantes! Nuestra especie, ha querido siempre tener un patrón que le guie para saber, en el campo de las medidas como moverse con cierta seguridad, y, poco a poco, hemos ido perfeccionando esos patrones acorde a los observados en la Naturaleza.

Unidades de medidas de peso

Rústica unidades de medida de líquidos
Nuestros predecesores nos han legado incontables unidades de medida de uso cotidiano que tendemos a utilizar en situaciones diferentes por razones de conveniencia. Compramos huevos por docenas, pujamos en la subasta en guineas, medimos las carreras de caballos en estadios, las profundidades oceánicas en brazas, el trigo en fanegas, el petróleo en barriles, la vida en y el peso de las piedras preciosas en quilates. Las explicaciones de todos los patrones de medida existentes en el pasado y en el presente llenan cientos de volúmenes.

Todo era plenamente satisfactorio mientras el comercio era local y sencillo. Pero cuando se inició el comercio internacional en tiempos antiguos, se empezaron a encontrar otras formas e contar. Las cantidades se median de diferente de un pais a otro y se necesitaban factores de conversión, igual que hoy cambiamos la moneda cuando viajamos al extranjero a un pais no comunitario. Esto cobró mayor importancia una vez que se inició la colaboración internacional de proyectos técnicos. La Ingenieria de precisión requiere una intercomparación de patrones exacta. Está muy bien decir a tus colaboradores en el otro lado del mundo que tienen que fabricar un componente de un avión que sea exactamente de un metro de longitud, pero ¿cómo sabes que su metro es el mismo que el tuyo?

No todas las medidas se regían por los mismos patrones
En origen, los patrones de medidas eran completamente locales y antropométricos. Las longitudes se derivaban de la longitud del brazo del rey o de la palma de la mano. Las distancias reflejaban el recorrido de un día de viaje. El Tiempo segúi las variaciones astronómicas de la Tierra y la Luna. Los pesos eran cantidades convenientes que podían llevarse en la mano o a la espalda.

Muchas de esas medidas fueron sabiamente escogidas y aún siguen con nostros hoy a pesar de la ubicuidad oficial del sistema decimal. Ninguna es sacrosanta. una está diseñada por conveniencia en circunstancias concretas.Muchas medidas de distancia se derivan antropomórficamente de las dimensiones de la anatomía humana:
El “pie” es la unidad más obvia dentro de esta categoría. Otras ya no resultan tan familiares. La “yarda” era la longitud de una cinta tendida desde la punta de la nariz de un hombre a la punta del dedo más lejano de su brazo cuando se extendía horizontalmente un lado. El “codo” era la distancia del codo de un hombre a la punta del dedo más lejano de su mano estirada, y varía entre los 44 y los 64 cm (unas 17 y 25 pulgadas) en las diferentes culturas antiguas que lo utilizaban.

La unidad náutica de longitud, la “braza” era la mayor unidad de distancia definida a partir de la anatomóa humana, y se definía como la máxima distancia las puntas de los dedos de un hombre con los brazos abiertos en cruz.
El movimiento de Mercaderes y Comerciantes por la región mediterránea en tiempos antiguos habría puesto de manifiesto las diferentes medidas de una misma distancia anatómica. Esto habría hecho difícil mantener cualquier conjunto único de unidades. la tradición y los hábitos nacionales era una poderosa fuerza que se resistía a la adopción de patrones extranjeros.
El problema más evidente de tales unidades es la existencia de hombres y mujeres de diferentes tamaños. ¿A quién se mide patrón? El rey o la reina son los candidatos obvios. Claro que, había que recalibrar cada vez que, el titular del trono cambiaba por diversos motivos.
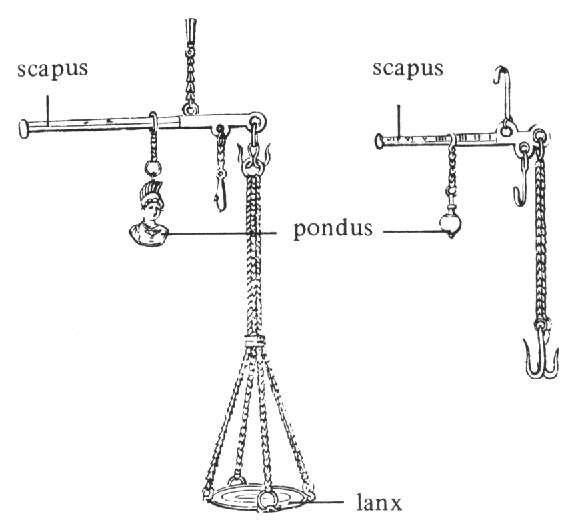
La depuración de patrones de medidas comenzó de decisiva en Francia en la época de la Revolución Francesa, a finales del siglo XVIII. La introducción de nuevos pesos y medidas conlleva una cierta comvulsión en la Sociedad y raramente es recibida con entusiamo por el pueblo. Así, dos años más tarde, se introdujo el “metro” como patrón de longitud, definido como la diezmillonésima de un cuadrante de meridiano terrestre. Aunque esta es una forma plausible de identificar un patrón de longitud, es evidente que no resulta práctica a efectos de comparación cotidiana. Consecuentemente, en 1795 las unidades fueron referidas directamente a objetos hechos de forma especial.

Siempre hemos tratado de medirlo todo, hasta las distancias que nos separan de las estrellas
Sí, siempre hemos tenido que medirlo todo. Al principio, unidad de masa se tomó el gramo, definido como la masa de un centímetro cúbico de agua a cero grados centígrados. Más tarde fue sustituido por el kilogramo (mil gramos), definido como la masa de mil centímetos cúbicos de agua… Finalmente, en 1799 se construyó una barra de metro prototipo junto con una masa kilogramo patrón, que fueron depositadas en los Archivos de la nueva República Francesa. Incluso hoy, la masa kilogramo de referencia se conoce como el “Kilogramme des Archives”.
Contar la historia aquí de todas las vicisitudes por las que han pasado los patrones de pesos y medidas en todos los paises, sería demasiado largo y tedioso. Sabemos que en Francia, en 1870, cuando se creo y reunió por primera vez en Paris la Comisión Internacional del Metro, con el fin de coordinar los patrones y supervisar la construcción de nuevas masas y longitudes patrón. El Kilogramo era la masa de un cilindro especial, de 39 milímetros de altura y de diámetro, hecho de una aleación de platino e iridio, protegido bajo tres campanas de cristal y guardado en una cámara de la Oficina Internacional de Patrones en Sèvres, cerca de Paris. Su definición es simple:

El kilogramo es la unidad de masa: es igual a la masa del prototipo internacional del kilogramo.
tendencia hacia la estándarización vio el establecimiento de unidades científicas de medidas. Como resultado medimos habitualmente las longitudes, masas y tiempos en múltiplos de metro, kilográmo y segundos. Cada unidad da una cantidad familiar fácil de imaginar: un metro de tela, un kilogramo de patatas. esta conveniencia de tamaño testimonia inmediatamente su pedigrí antropocéntrico. Pero sus ventajas también se hacen patentes cuando empezamos a utilizar dichas unidades para describir cantidades que corresponden a una escala superior o inferior a la humana:

Los átomos son diez millones de veces más pequeños que un metro. El Sol una masa de más de 1030 kilogramos. Y, de esa manera, los humanos hemos ido avanzando en la creación, odeando patrones todos y, no digamos en la medida de las distancias astronómicas en las que, el año-luz, la Unidad Astronómica, el Parsec, el Kiloparsec o el Megaparsec nos permiten medir las distancias de galaxias muy lejanas.
Lo que decimos siempre: Nuestra curiosidad nunca dejará de querer saber el por qué de las cosas y, siempre tratará de racionalizarlo todo para hacernos fácil nuestras interacciones con el mundo que nos rodea. Y, aunque algunas cosas al principio nos puedan parecer mágicas e ilusorias, finalmente, si nuestras mentes la pensaron… ¡Pueden llegar a convertirse en realidad!
emilio silvera
Oct
10
Una idea que persiste (Pendiente de ser confirmada)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Vida ~
Clasificado en El Universo y la Vida ~
 Comments (1)
Comments (1)

Un día de hace unos veinte años, allá por el año 1996, el pueblo americano escuchaba con asombro a su presidente, Clinton por aquel entonces, que en marte podía existir vida. La noticia de que un antiguo meteorito caido en la Tierra y proveniente de dicho planeta, así parecía confirmarlo al contener fósiles de vida microbiana. Como podreis comprender, aquello impactó en la opinión pública de todo el mundo y, la noticia, fue objeto de todas las primeras planas y tambien, de todas las conversaciones en los corrillos en el trabajo, en el café, por las calles y en familia. ¡Vida en otro planeta!
Aunque no lo podamos saber todo y no estemos al tanto de lo que pasa en el mundo científico (las noticias saltan cuando hay un descubrimiento relevante), lo cierto es que, durante los últimos años los científicos han llevado a cabo una espectacular puesta al día de sus ideas sobre el origen de la vida. Todos hemos podido leer en los libros de texto que, la vida, comenzó temprano en nuestro planeta. Según todos los indicios (los fósiles encontrados en las rocas más antiguas así lo afirman), la vida ha estado presente en la Tierra desde hace ya unos cuatro mil millones de años.

Encuentran microbios a dos kilómetros bajo tierra en un cráter en EEUU
Parece ahora que los primeros organismos terrestres vivían en el subsuelo profundo al calor de la joven Tierra, enterrados en rocas calentadas geotérmicamente en condiciones similares a las que podríamos encontrar en una olla a presión. Sólo posteriormente migraron estos organismos a la superficie. Sirprendentemente, los descendientes de esos microbios primordiales aún están allí, a kilómetros de profundidad bajo nuestros pies.
Hace algunos años nadie podía sospechar que la vida pudiera estar presente en un ambiente tan inhóspito escondidos en las rocas bajo la superficie de la Tierra y… ¿de Marte?.

Fotografía del meteorito ALH 84001
¿Cómo empezó la vida exactamente? ¿Qué procesos físicos químicos pueden transformar la materia “inerte” en un organismo viv0? Esta compleja pregunta sigue siendo uno de los más grandes misterios de la naturaleza y quizás, el reto científico también mayor. Ejercitos de químicos y biólogos desde hace años, están abordando el complejo problema y tratan de desvelar el secreto tan celosamente guardado por la Naturaleza. Muchos de ellos, han tenido que concluir diciendo que, las leyes de la Naturaleza están predispuestas a favor de la vida y dicen que la vida se formará y surgirá en todos aquellos lugares que tengan las condiciones idóneas para ello.
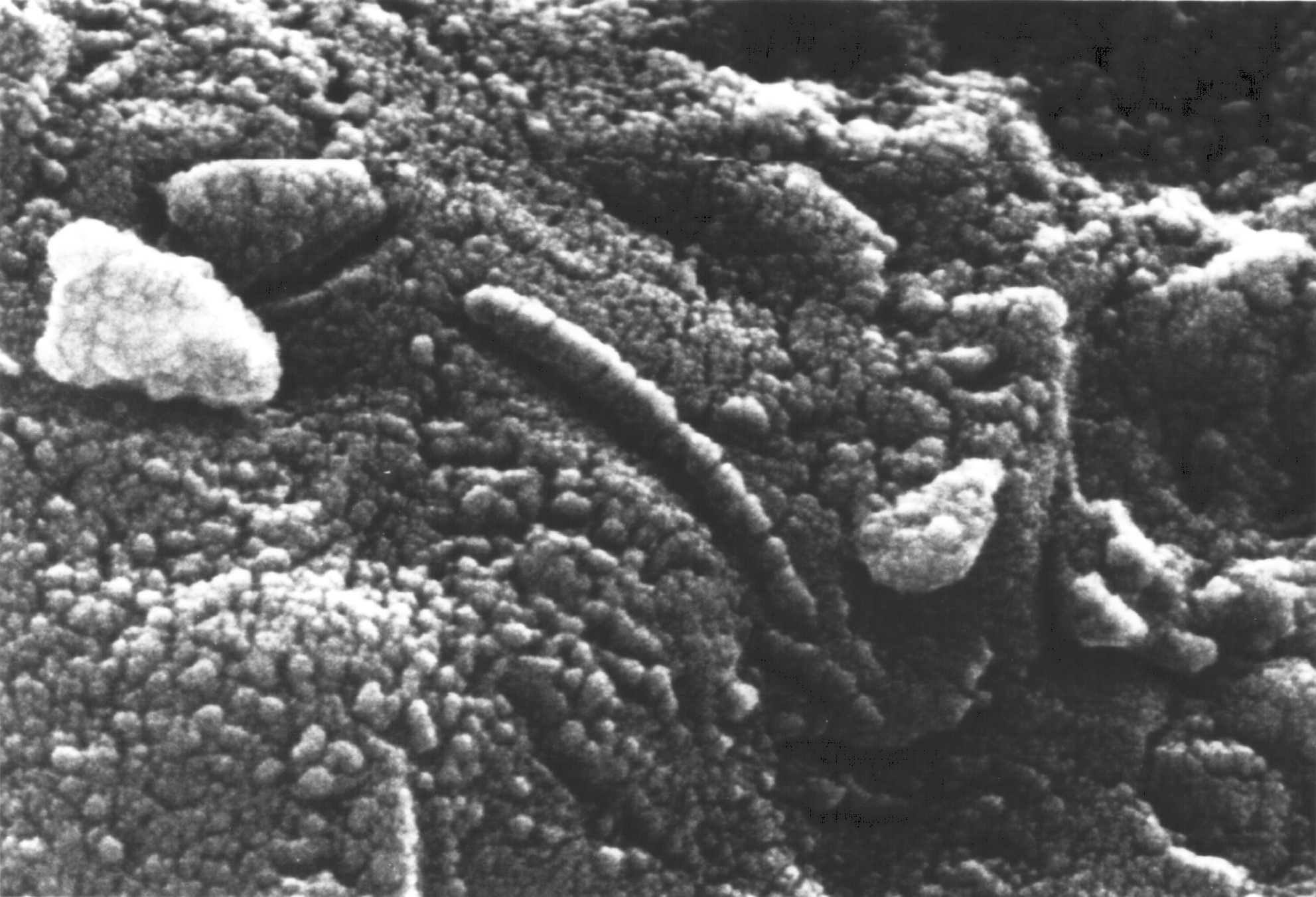
Vista microscópica de la estructura interna del ALH 84001
Así que, no sólo en la Tierra o Marte, también la vida podría estar presente en cualquier luna o planeta que, situado en la zona habitable de la estrella que los acoge, con atmósfera y elementos químicos y los demás ingredientes necesarios (Carbono, Hidrógeno,Oxígeno, Nitrógeno…) además de la presencia también de alguna clase de actividad tectónica-volcánica, una capa de ozono, la presencia de gases con efecto invernadero, agua líquida, ¿un planeta gigante?, existencia de un campo magnético…
La tectónica de placas y el vulcanismo activo de nuestro planeta habrían tenido un importante para mantener el clima . Estos procesos actúan como un gigantesco termostato natural que regula la cantidad de dióxido de carbono de la atmósfera, y manteniendo el efecto invernadero a raya.
Los gases de efecto invernadero tan satanizados hoy en día, son absolutamente imprescindibles para la vida. Los más importantes son el dióxido de carbono, vapor de agua y el metano que atrapan el calor del Sol que de otra forma escaparía al espacio. Sin estos gases en la atmósfera, el planeta entero sería un gigantesco congelador.
La capa de ozono es crítica para las plantas y animales bloqueando la mayor parte de estos nocivos rayos de alta energía procedentes del Sol.

Últimamente nos hablan con cierta frecuencia de que han encontrado vestigios de agua líquida en Marte y también la encontraron el planeta enano del proyecto Horizont, Se me da que el agua, es un elementos que prolifera, como la vida misma, por muchos lugares que ni podemos sospechar.
El agua líquida es absolutamente imprescindible para la vida como la conocemos. Los océanos proporcionan el ambiente líquido perfecto para que proliferen los orgamisnos vivos. A pesar de todo, existen algunos organismos vivos exóticos capaces de sobrevivir en ambientes mucho más secos. El agua se filtra a gran profundidad en las rocas actuando además como natural en los movimientos de las placas tectónicas.
Este es uno de los aspectos más importantes para que la vida pueda desarrollarse. La zona habitable de un sistema estelar se suele definir como aquella región del sistema en la que el agua puede existir en forma líquida. Distancias menores a la estrellas provocarían que los océanos hirviesen y se secasen, distancias mayores causarían que los océanos se congelasen.

Algunos científicos opinan que la existencia de un planeta masivo como Júpiter en nuestro Sistema solar solar protege a la Tierra de impactos de asteroides y cometas. Júpiter actuaría como un escudo, absorbiendo la mayoría de impactos de asteroides y cometas, capaces de provocar una enorme destrucción en la biosfera.
Un planeta habitable necesitaría un campo magnético capaz de protegerlo de la embestida de partículas cargadas del viento estelar desviando la corriente. Sin la presencia de un campo magnético, el viento solar o estelar podría arrancar la atmósfera del planeta que escaparía al espacio. Un campo magnético también protege de la radiación cósmica…
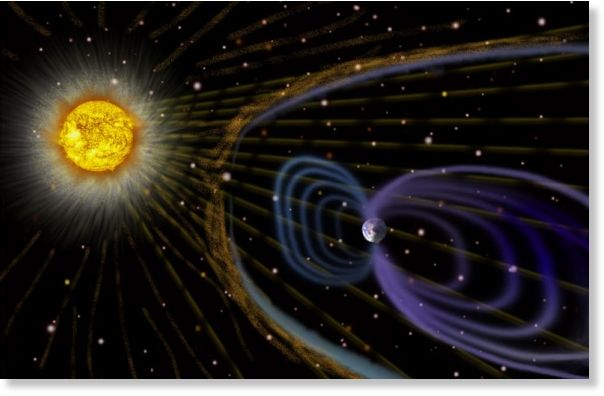
La creencia en que la vida está inscrita en las leyes de la Naturaleza trae un débil eco de una era religiosa pasada, de un universo concebido para ser habitado por criaturas vivas. Muchos científicos menosprecian tales ideas, e insisten en que el origen de la vida fue un accidente anómalo de la química que sólo se dio en la Tierra; y que la posterior emergencia de organismos complejos, incluyendo los seres conscientes, es así mismo un resultado puramente fortuito de una gigantesca lotería cósmica. En este debate está en juego el lugar mismo de la Humanidad en el Cosmos: ¿Quiénes somos y dónde encajamos dentro del gran esquema?

Bueno, ahora estamos vigilantes y queremos desvelar ese misterio. En cuanto a que todo esto es el resultado de una gran loteria cósmica… me parece que no. En una loteria sale un número y, sin embargo, en lo relativo a la vida, sabemos que actualmente sólo viven en nuestro planeta aproximadamente un uno por ciento de todas las especies que lo han poblado a lo largo de su existencia. Y, si es así (que lo es), ¿cómo es posible esa diversidad de criaturas en un caso fortuito? ¿No será más lógico pensar que, la vida, es consustancial de la dinámica del Universo?
Hemos conformado un modelo del universo y de él partimos para poder explicar su Historia. Hemos inventado un Big Bang que, en parte, nos explica el suceso de la presencia del universo y de cómo pudo surgir. Su nacimiento explosivo estuvo acompañado por un inmenso destello de calor intenso. Durante la primera fracción se segundo emergieron las fuerzas físicas básicas y las partículas fundamentales de la materia. Al cabo de este primer segundo, los materiales esenciales del Cosmos ya estaban formados. El espacio está repleto por todas partes de una sopa de partículas subatómicas -protones, neutrones y electrones– bañadas en radiación a una temperatura de dies mil millones de grados.
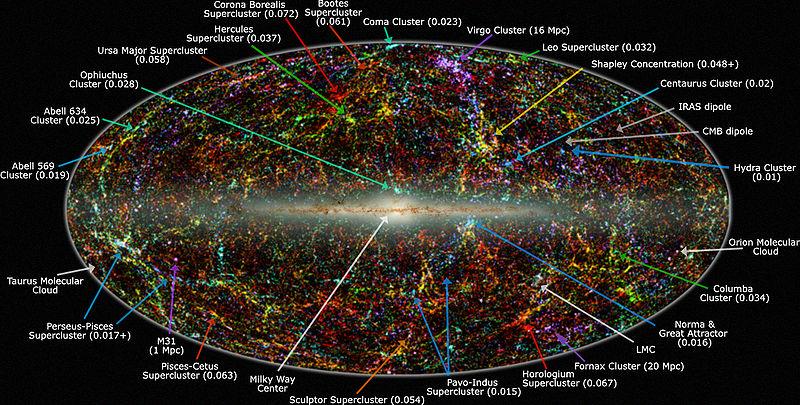
Bueno, lo que en realidad estamos llamando el principio aquí es el universo cuando la temperatura rondaba los 100,000,000,000 K. El universo ya había existido al menos por una pequeña fracción de segundo y estaba dominado por radiación con unas pequeñas trazas de materia. La radiación estaba en forma de fotones, neutrinos y antineutrinos. La materia estaba en forma de electrones, positrones y una pequeña concentración de protones y neutrones (denominados nucleones) – aproximadamente un nucleón por cada 1,000 millones de partículas-.

A estas temperaturas y densidades tan extremas (la densidad equivalía a unos 3.800 millones de veces la densidad del agua), todas estas entidades se comportan como partículas. Eso significa que están todo el tiempo colisionando entre ellas, casi como lo harían un montón de canicas que estuvieran bien empaquetadas en un container. En el universo primitivo no existían “paredes” físicas que contuvieran a esas partículas, sino que el elevado número de colisiones y la rapidez de éstas jugaban perfectamente el papel de “paredes del universo”. Sin embargo, esas “paredes” no eran estáticas, sino que a medida que se producían las colisiones el universo aumentaba de tamaño. La expansión del universo producía una disminución de la densidad de energía que tenía que distribuirse en un volumen cada vez mayor. Este proceso implicaba a su vez una disminución de la temperatura del universo, proceso que continúa ocurriendo hoy en día.

Las colisiones entre partículas tenían tres importantes consecuencias. La primera es que el universo estaba en equilibrio térmico. Para dar al lector una idea de lo que esto significa, vamos a fijarnos en un vaso de agua a 40 grados. La temperatura de un objeto es una medida de la energía media del movimiento (energía cinética) de sus moléculas. Pero no todas las moléculas la misma energía cinética correspondiente a una temperatura de 40 grados, sino que existen moléculas con menos energía y moléculas con más energía.
PRIMER CAMINO
Los núcleos de deuterio colisionan con un protón formando 3He, y seguidamente con un neutrón formando 4He

SEGUNDO CAMINO
El deuterio colisiona primero con un neutrón formando 3H (habitualmente conocido como tritio), y posteriormente con un protón para formar de nuevo 4He

Este núcleo fue el más pesado que se formó en el universo primitivo, debido a que en el momento en que esto fue posible, la densidad de energía ya era demasiado baja para permitir que los núcleos colisonarán con suficiente energía para fundirse. En el momento en que comenzó la nucleosíntesis, la abundancia relativa de protones y neutrones era: 13% de neutrones y 87% de protones. Todos los neutrones fueron utilizados para formar los núcleos de Helio. Los protones quedarían de esa manera como núcleos de hidrógeno. Por lo tanto, tenemos que en el momento en que se completó la nucleosíntesis primigenia, el universo consistía en prácticamente un 25% de He y un 75% H (en peso) con ligeras trazas de otros elementos ligeros.
El paso final en la formación de los elementos fue la captura de los electrones libres por parte de los núcleos para formar los átomos neutros (proceso conocido curiosamente como recombinación a pesar de que es la primera vez que se ligaban electrones y núcleos).

Pero los electrones tenían aún suficiente energía para y el proceso de recombinación no ocurriría de forma masiva hasta que transcurrieran unos 700,000 años. La captura de los electrones para formar los átomos tuvo una consecuencia importantísima: sin electrones libres, la radiación electromagnética (los fotones) ya no tenían con quién interactuar y el universo se volvería transparente al paso de ésta. Esto significó que los fotones serían capaces de expandirse junto con el universo. Esos fotones que acabaron por ser libres tenían energías altísimas que se traducía en longitudes de onda muy cortas. Pero la expansión del universo causó el alargamiento de esta longitud de onda. Esos fotones de longitud de onda alargada debida a la expansión son a los que nos referimos cuando hablamos del fondo de microondas. Éste es un remanente del Big Bang. Hemos sido capaces de medir la intensidad de este fondo de radiación que se ajusta casi perfectamente a lo que predicen los cálculos teóricos. Ésta ha sido una de las evidencias más rotundas a favor de la imagen del universo que proporciona el modelo del Big Bang.

Unos doscientos millones de años más tarde de todos aquellos sucesos, el universo estaba más frío y los átomos se unieron para formar las primeras estrellas que comenzaron a brillar en el espacio interestelar del jóven universo. Así, durante diez mil millones de años, se fueron transmutando nuevos materiales en los nucleares, las estrellas masivas habían explosionado y dejado el rastro de nubes moleculares gigantescas, nacieron nuevas estrellas de II generación situadas en Sistemas solares que posibilitaron, presididos por una estrella mediana, amarilla de la clase G2V, que en un planeta situado a la distancia adecuada y con todos los ingredientes y parámetros necesarios, surgieran seres vivios a partir de la materia “inerte” evolucionada y, en alguna de aquellas especies, cuatro mil años más tarde, se llegó a adquirir la conciencia.
Personajes como Fred Hoyle, Brandon Carter, Eugene Wigner, Erwin Schrödinger, Martin Rees, Bernard Carr, Freeman Dyson y Tommy Gold, Lewis Wolpert y Sydney Brenner, Jhon Coway y Manfred Eigen y Grahan Cairns-Smith. Todos ellos grtandes especialistas en sus campos que abarcaban desde la biología, las matemáticas, la genética hasta la astronomía y la astrofísica…Todos ellos y más tarde otros, como Casrl Sagan, creyeron ciegamente en la existencia de la vida por todo el universo. Para ellos (y para mí también), era una regla inamovible y consustancial con la dinámica y el ritmo que marca el Universo para que la Vida, esté en él presente.

La historia científica de la vida es una narración apasionante que, correctamente explicada, nos ayuda a comprender no sólo nuestro pasado biológico sino también la Tierra y toda la vida que nos rodea en la actualidad. Esa diversidad biológica es el producto de casi cuatro mil millones de años de evolución. Somos parte de ese legado; al intentar comprender la historia evolutiva de la vida, comenzamos a entender nuestro propio lugar en el mundo y nuestra responsabilidad como administradores de un planeta que nos dio cobijo y al que nos tuvimos que adaptar lo mismo que él, el planeta, se adaptó a la presencia de la vida que, de alguna manera cambió su entorno climático, precisamente debido, a esa presencia viviente que generó las precisas condiciones para poder estar aquí.
La historia de la vida tiende a relatarse (no pocas veces) al estilo de la genealogía de Abraham: las bacterias engendraron a los protozoos, los protozoos engendraron a los invertebrados, los invertebrados engendraron a los peces, y así sucesivamente. Tales listas de conocimientos adquiridos pueden memorizarse, pero no dejan mucho espacio para pensar. La cuestión no es tan sencilla y los descubrimientos de la paleontología, la más tradicional de las empresas científicas, se entrelazan con nuevas ideas nacidas de la biología molecular y la geoquímica.

Los huesos de los Dinosaurios son grandes y espectaculares y hacen que los que los contemplan (niños y mayores), abran los ojos como platos, asombrados de tal maravilla. Pero, aparte del tamaño de sus habitantes, el mundo de los dinosaurios se parecía mucho al nuestro. Contrasta con él la historia profunda de la Tierra, que nos cuentan fósiles microscópicos y sutiles señales químicas y que es, pese a ello, un relato dramático, una sucesión de mundos desaparecidos que, por medio de la transformación de la atmósfera y una evolución biológica, nos llevan hacia el mundo que conocemos hoy.
Pero, ¿cómo podemos llegar a comprender acontecimientos que se produjeron hace mil millones de años o más? Una cosa es aprender que en las llanuras mareales de hace mil quinientos millones de años vivían bacterias fotosintéticas, y otra muy distinta cómo se infiere que unos fósiles microscópicos pertenecen a bacterias fotosintéticas, cómo se averigua que las rocas que los rodean se formaron en antiguas llanuras mareales y cómo se estima su edad en mil quinientos millones de años.

El leitmotiv epistemológico de cómo sabemos lo que creemos que sabemos, en realidad, aparece de manera espontánea a base de mucho estudio de campo, investigación exhaustiva en los más dispares rincones de la Tierra y, un profundo estudio concatenado en el tiempo de todo aquello que, en cada exploración pueda ir apareciendo. En tanto que empresa humana, estamos inmersos también en un relato de exploración que se extiende desde el espacio interior de las moléculas al espacio literalmente exterior de Marte y otros planetas.
Uno de los temas más claros de la historia evolutiva es el carácter acumulativo de la diversidad biológica. Las especies individuales (al menos las de los organismos nucleados) aparecen y desaparecen en una sucesión geológica de extinciones que ponen de manifiesto la fragilidad de las poblaciones en un mundo de competencia y cambio ambiental –de formas de vida con una morfología y fisiología características- es una historia de acumulación. La visión de la evolución a gran escala es indiscutiblemente la de una acumulación en el tiempo gobernada por las reglas de funcionamiento de los ecosistemas. La serie de sustituciones que sugieren los enfoques al estilo de la genealogía de Abraham no consigue captar este atributo básico de la historia biológica.

Así, creemos saber que la vida nació por mediación de procesos físicos en la Tierra primigenia. Estos mismos procesos –tectónicos, oceanográficos y atmosféricos- sustentaron la vida era tras era al tiempo que modificaban continuamente la superficie de la Tierra. Por fin la vida se expandió y se diversificó hasta convertirse en una fuerza planetaria por derecho propio, uniéndose a los procesos tectónicos y físico-químicos en la transformación de la atmósfera y los océanos.


Dondequiera que choquen las relativamente rápidas placas tectónicas oceánicas con las enormes placas continentales, se forman cadenas montañosas en continua elevación. Los ejemplos más espectaculares se subducción y formación montañosa son, respectivamente, la placa del Pacífico sumergiéndose en las profundas fosas del Asia oriental, y el Himalaya, que se eleva por el choque de las placas índica y euroasiática. Todo forma parte del proceso que llevó a la vida.
Para mí y para cualquiera que emplee la lógica de la ciencia que se guía por los hechos probados, el surgimiento de la vida como una característica definitoria –quizá la característica definitoria- de nuestro planeta es algo extraordinario.

¿Quién podría negar que somos parte del Universo?
¿Cuántas veces ha ocurrido lo mismo en la vastedad del Universo? Es lo primero que se me viene a la mente cuando (en la noche silenciosa, oscura y tranquila lejos del bullicioso ambiente de las ciudades y de su molesta contaminación lumínica), miro hacia las estrellas brillantes del cielo que, muy lejanas en regiones remotas, también como nuestro Sol, están rodeadas de mundos que, como el nuestro, habrán tenido la misma posibilidad que la Tierra para que la vida, pudiera surgir.
Hacer aquí un recorrido pormenorizado del largo camino que la vida ha tenido que recorrer, y dibujar un esquema a modo de un árbol de la vida, es imposible. El presente trabajo trata simplemente, de dejar una idea básica de cómo la vida llegó aquí, al planeta Tierra, y, de cómo pudo evolucionar con el paso del tiempo y dentro de su rica diversidad.

![[clip_image021[5].jpg]](http://lh6.ggpht.com/_qFJEJ54NBZo/S37k52BYcEI/AAAAAAAAKoQ/DSlNwb9hgio/s1600/clip_image021%5B5%5D.jpg)
Estos escenarios son precursores de vida
Los expertos si han construido un árbol de la vida a partir de comparaciones ente secuencias de nucleótidos de genes de diversos organismos, las plantas y los animales quedan reducidos, en ese árbol, a brotes en la punta de una sola de las ramas. La mayor diversidad de la vida y, por extensión, la mayor parte de su historia, es microbiana. Así lo atestiguan todos y cada uno de los hallazgos encontramos en las rocas precámbricas que contienen fósiles de aquellas primeras formas de vida.
Hasta que la evolución de la materia llegó… ¡Hasta nosotros!
Y, una cosa está muy clara y no se presta a ninguna clase de dudas: Las Bacterias y las Arqueas, son los arquitectos de los ecosistemas terrestres.
Biólogos expertos indiscutibles de probada valía y reconocido prestigio, han llegado a sugerir que los genes de los organismos actuales contienen el relato completo de la historia evolutiva. Pero, de ser así se trataría, como en las historias de Shakespeare, de relatos limitados a los vencedores de la vida. Sólo la paleontología nos puede hablar de los trilobites, los dinosaurios y otras maravillas biológicas que ya no adornan la faz de la Tierra.
Cualquiera que sea la ctividad química notable que haya podido tener lugar en la Tierra primordial o en algún otro planeta situado en cualquiera de los miles de millones de galaxcias que por el Universo pululan, la vida ha podido ser desencadenada no por una vorágine molecular como tal, sino -¡de algún modo!- por la organización de la información que ha dado la misma Naturaleza a la materia para que sepa, seguir su destino desde lo inerte hasta los pensamientos.
De ello, os hablaré en próximos trabajos. Pero eso sí, aquí hablamos de lo que creemos que sabemos y, como ha ocurrido en otras muchas oportunidades… ¡Podríamos estar equivocados! Esa es la obligación de la Ciencia, precisamente, descubrir los errorres para ir poniendo cada cosa en su lugar. Mientras tanto, sigamos especulando.
emilio silvera
Oct
10
¿Cuánta materia vemos?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en ¿Cuánta materia vemos? ~
Clasificado en ¿Cuánta materia vemos? ~
 Comments (0)
Comments (0)
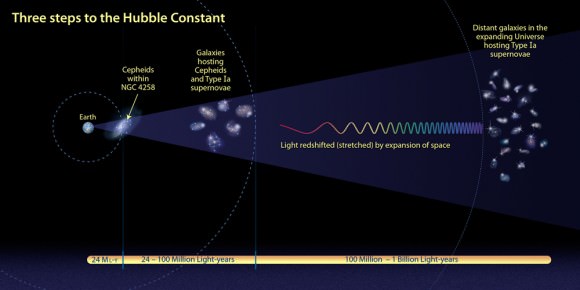
La constante de Hubble en función de la Densidad Crítica
La cantidad total de Materia del Universo se da generalmente en términos de una cantidad llamada Densidad Crítica, denotada por Omega (Ω). Esta es la densidad de la materia que se necesita para producir un universo plano. Si la Densidad efectivamente observada es menor o mayor que ese parámetro, en el primer caso el Universo es abierto, en el segundo es cerrado. La Densidad Crítica no es muy grande; corresponde aproximadamente a un protón por metro cúbico de espacio. Puede que no parezca mucho, dado el número inmenso de átomos en un metro cúbido de lodo, pero no debemos olvidar que existe una gran cantidad de espacio “vacío” entre las galaxias.

Cuando contemplamos imágenes como la de arriba, nos resulta engoñoso y no imaginamos las inmensas distancias que las separan. Las galaxias están muy retiradas las unas de las otras. Andrómedra y la Vía Láctea están a 2,3 años-luz perteneciendo al mismo Grupo Local.
Algunos números que definen nuestro Universo:
- El de fotones por protón
- La razón densidades de Materia Oscura y Luminosa.
- La Anisotropía de la Expansión.
- La falta de homogeneidad del Universo.
- La Constante Cosmológica.
- La desviación de la expansión respecto al valor crítico.
- Fluctuaciones de vacío y sus consecuencias.
- ¿Otras Dimensiones?

En las últimas medidas realizadas, la Densidad crítica que es la densidad necesaria para que la curvatura del universo sea cero, ha dado el resultado siguiente: r0 = 3H02/8pG = 1.879 h2 10-29 g/cm3, que corresponde a una densidad tan baja la de la masa de 2 a 3 átomos de hidrógeno por metro cúbico (siempre, por supuesto obviando la incertidumbre en la constante de Hubble).
Estimar la cantidad de materia luminosa del universo es una cosa muy fácil de hacer. Sabemos el brillo que tiene una estrella media, así que podemos hacer una estimación del de estrellas de una galaxia distante. Podemos contar entonces el número de galaxias en un volumen dado de espacio y sumar las masas que encontramos. Dividiendo la masa por el volumen del espacio obtenemos la densidad media de materia en ese volumen. Cuando llevamos a cabo esta operación, obtenemos que la densidad de la materia luminosa es aproximadamente entre el uno o dos % menor de la densidad crítica; es decir, menos de lo que se necesita para cerrar el universo.


Por otro lado, está lo bastante cerca del valor crítico para hacer una pausa. Después de todo, esta fracción podría haber sido en principio de una billonésima o trillonésima, y también podría haber sucedido que fuese un millón de veces la materia necesaria para el cierre. ¿Por qué, entre todas las masas que podría tener el universo, la masa de materia luminosa medida está cerca del valor crítico?

Claro que el hecho de que la materia luminosa medida esté tan cercana al valor crítico, simplemente podría deberse a un accidente cósmico; las cosas sencillamente “resultan” de ese modo. Me costaría mucho aceptar una explicación y supongo que a otros también. Es tentador decir que el Universo tiene en realidad la masa crítica, pero que de algún modo no conseguimos verla toda.
Como resultado de esta suposición, los astrónomos comenzaron a hablar de la “masa perdida” con lo que aludían a la materia que habría llenado la diferencia entre las densidades observadas y la crítica. Tales teorías de “masa perdida”, “invisible” o, finalmente “oscura”, nunca me ha gustado, toda vez que, hablamos y hablamos de ella, damos por supuesta su existencia sin haberla visto ni saber, exactamente qué es, y, en ese plano, parece como si la Ciencia se pasara al ámbito religioso, la fe de creer en lo que no podemos ver ni tocar y, la Ciencia, amigos míos, es otra cosa.

Tendremos que imaginar satélites y sondas que, de alguna manera, puedan detectar grandes halos galácticos que encierren la tan buscada materia oscura y que, al parecer, hace que nuestro Universo sea lo conocemos y, es la responsable del ritmo al que se alejan las galaxias, es decir, la expansión del Universo.
Esos halos, tendrían muchas veces las masas que podemos ver en la Materia luminosa de las estrellas, planetas, galaxias y nosotros mismos. La teoría de la materia oscura y su presencia en cúmulos y supercúmulos ha sido “descubierta” (o inventada para tapar nuestra ignorancia) en época relativamente cercana para que prevalezca entre los astrónomos la unanimidad respecto a su contribución a la masa total del universo. El debate continúa, está muy vivo y, es el tema tan candente e importante que, durará bastante tiempo mientras algún equipo de observadores no pueda, de una vez por todas, demostrar que, la “materia oscura” existe, que nos digan donde está, y, de qué está conformada y como actúa. Claro que, cuando se haga la suma de materia luminosa y oscura, la densidad de la masa total del universo no será todavía mayor del 30% del valor crítico. A todo esto, ocurren sucesos que no podemos explicar y, nos preguntamos si en ellos, está implicada la “Materia oscura”, o, por el contrario, está tirando de nuestro Universo, otros universos vecinos.

Inusual colisión de enanas blancas y también, se ha podido detectar la más abarrotada colisión de cúmulos galácticos que han sido identificados al combinar información de tres diferentes telescopios. El resultado brinda a los científicos una posibilidad de aprender lo que ocurre con algunos de los más grandes objetos en el universo que chocan en una batalla campal cósmica de inusitada fuerza y descomunal emisión de energía.

Usando del Observatorio de rayos-X Chandra, el Telescopio Espacial Hubble y el Observatorio Keck de Hawai, los astrónomos fueron capaces de determinar la geometría tridimensional y el movimiento en el sistema MACSJ0717.5+3745 localizado a 5.4 mil millones de luz de la Tierra. Los investigadores encontraron que cuatro distintos cúmulos de galaxias están envueltos en una triple fusión, la primera vez que un fenómeno así es documentado.

La composición de imagen (arriba) muestra el cúmulo de galaxias masivo MACSJ0717.5+3745. El color del gas caliente está codificado con colores mostrar su temperatura. El gas más frío es mostrado como un púrpura rojizo, el gas más caliente en azul y las temperaturas intermedias en púrpura. Las repetidas colisiones en el cúmulo son causadas por una corriente de galaxias, polvo y “materia oscura” -conocida filamento- de 13 millones de años luz.
Se han obtenido Imágenes (MACSJ0717) que muestran cómo cúmulos galácticos gigantes interactúan con su entorno en escalas de millones de años luz. Es un sistema hermoso para estudiar cómo los cúmulos crecen mientras el material cae en ellos a lo largo de filamentos. Simulaciones por ordenador muestran que los cúmulos de galaxias más masivos deben crecer en regiones donde filamentos de gran escala de gas intergaláctico, galaxias, y materia desconocida intersectan, pero…
¿Cuál debe ser la Masa del Universo?

Alan Guth
Claro que la idea de masa perdida se introdujo porque la densidad observada de la materia del universo está cerca del valor crítico. Sin embargo, hasta comienzos de los ochenta, no se tuvo una razón teórica firme para suponer que el universo tenía efectivamente la masa crítica. En 1981, Alan Guth, publicó la primera versión de una teoría que entonces se ha conocido como “universo inflacionista”. Desde entonces, la teoría ha sufrido numerosas modificaciones técnicas, pero los puntos centrales no han cambiado.
nuestra conversación de hoy, diremos que el aspecto principal del universo inflacionista es que estableció por primera vez una fuerte presunción de que la masa del universo tenía realmente el valor crítico. Esta predicción viene de las teorías que describen la congelación de la fuerza fuerte en el segundo 10-35 del Big Bang. los otros muchos procesos en marcha en ese tiempo estaba una rápida expansión del universo, un proceso que vino a ser conocido como inflación. Es la presencia de la inflación la que nos lleva a la predicción de que el universo tiene que ser plano.

Abell 370 La lente gravitacional distorsiona la Imagen y nos enseña, a la derecha, algo que nos parece una inmensa cuerda cósmica , ¿que podrá ser en realidad? la materia a lo largo y ancho del universo se reparte de manera que, se ve concentrada en cúmulos de galaxias y supercúmulos que son las estructuras más grandes conocidas y, dentro de ellas, están todos los demás objetos que existen. Claro que, deajndo a un lado esas fluctuaciones de vacío y, la posible materia desconocida.
El proceso mediante el cual la fuerza fuerte se congela es un ejemplo de un cambio de fase, similar en muchos aspectos a la congelación del agua. el agua se convierte en hielo, se expande; una botella de leche explotará si la dejamos en el exterior en una noche de invierno de gélido frío. No debería ser demasiado sorprendente que el universo se expanda del mismo modo al cambiar de fase.

La distancia a una galaxia lejana se determina estudiando la luz proveniente de estrellas de tipo Cefeidas Variables. El expectro de la luz estelar revela la velocidad a la que se mueve la galaxia (Efecto Doppler) y la cantidad de expansión que ha sufrido el universo que la luz salió de su fuente.
Lo que es sorprendente es la enorme amplitud de la expansión. El tamaño del Universo aumentó en un factor no menor de 1050. Este es tan inmenso que virtualmente no tiene significado para la mayoría de la gente, incluido yo mismo que, no pocas veces me cuesta asimilar esas distancias inconmensurables del Cosmos. Dicho de otra manera, pongamos, por ejmplo, que la altura de los lectores aumentara en un factor tan grande como ese, se extenderían de un extremo al otro del Universo y, seguramente, faltaría sitio. Incluso un sólo protón de un sólo átomo de su cuerpo, si sus dimensiones aumentaran en 1050, sería mayor que el mismo universo. En 10-35 segundos, el universo pasó de algo con un radio de curvatura mucho menor que la partícula elemental más pequeña a algo como el tamaño de una naranja grande. No es extraño que el inflación esté ligado a este proceso.
Comparación entre un modelo de expansión desacelerada (arriba) y uno en expansión acelerada (abajo). La esfera de referencia es proporcional al factor de escala. El universo observable aumenta proporcionalmente al tiempo. En un universo acelerado el universo observable aumenta más rápidamente que el factor de escala con lo que cada vez podemos ver mayor del universo. En cambio, en un universo en expansión acelerada (abajo), la escala aumenta de manera exponencial mientras el universo observable aumenta de la misma manera que en el caso anterior. La cantidad de objetos que podemos ver disminuye con el tiempo y el observador termina por quedar aislado del resto del universo.
Cuando ( mucho tiempo ya) leí por primera vez acerca del universo inflacionario, experimenté dificultades para poder asimilar el índice de inflación. ¿No violaría un crecimineto tan rápido las reglas impuestas por la relatividad de Eintien que marcaban el límite de la velocidad en el de la luz en el vacío? Si un cuerpo material viajó de un extremo de una naranja a otro en 10-35 segundos, su velocidad excedió a la de la luz en una fracción considerable.

Claro que, con esto pasa como pasó con estos “veloces” neutrinos que, algunos decían haber comprobado que corrían más rápidos que la luz, y, sin embargo, todo fue un error de cálculo en el que no se tuvieron en algunos parámetros presentes en las mediciones y los aparatos que hacían las mismas. Aquí, podría pasar algo parecido y, la respuesta la podemos encontrar en aquella analogía con la masa de pan. Durante el período de inflación es el espacio mismo -la masa de pan- lo que está expandiéndose. Ningún cuerpo material (acordaos que en aquella masa estaban incrustadas las uvas que hacían de galaxias y, a medida que la masa se inflaba, las uvas -galaxias- se alejaban las unas de las otras pero, en realidad, ninguna de estas uvas se mueven, es la masa lo que lo hace.

El Universo se expande
Las reglas contra los viajes a mayor velocidad que la de la luz sólo se aplican al movimiento del espacio. Así no hay contradicción, aunque a primera vista pueda parecer que sí. Las consecuencias del período de rápida expansión se pueden describir mejor con referencia a la visión einsteniana de la gravitación. de que el universo tuviera 10-35 segundos de edad, es de suponer que había algún tipo de distribucón de la materia. A cauda de esa materia, el espacio-tiempo tendrá alguna forma característica. Supongamos que la superficie estaba arrugada antes de que se produjera la inflación. Y, de esa manera, cuando comenzó a estirarse, poco a poco, tomó la forma que podemos detectar de “casi” plana conforme a la materia que contiene.

En todo esto, hay un enigma que persiste, nadie sabe contestar cómo, a pesar de la expansión de Hubble, se pudieron formar las galaxias. La pregunta sería: ¿Qué clase de materia estaba allí presente, que, la materia bariónica no se expandiera sin rumbo fijo por todo el universo y, se quedara el tiempo suficiente para formar las galaxias? Todo ello, a pesar de la inflación de la que hablamos y que habrái impedido su formación. Así que, algo tenía que existir allí que generaba la gravedad necesaria para retener la materia bariónica hasta que esta, pudo formar estrellas y galaxias.
No me extrañaria que, eso que llaman materia oscura, pudiera ser como la primera fase de la materia “normal” que, estándo en una primera fase, no emite radiaciones ni se deja ver y, sin embargo, sí que genera la fuerza de Gravedad para que nuestro Universo, sea tal como lo podemos observar.

En imagenes como , los “expertos” nos dicen cosas como:
“La materia oscura en la imagen de varias longitudes de onda de arriba se muestra en un falso color azul, y nos enseña detalles de como el cúmulo distorsiona la luz emitida por galaxias más distantes. En de gas muy caliente, la materia normal en falso color rojo, son fruto de los rayos-X detectados por el Observatorio de Rayois X Chandra que orbita alrededor de la Tierra.”
Algunas galaxias individuales dominadas por materia normal aparecen en colores amarillentos o blanquecinos. La sabiduría convencional sostiene que la materia oscura y la materia normal son atraídas lo mismo gravitacionalmente, con lo que deberían distribuirse homogéneamente en Abell 520. Si se inspecciona la imagen superior, sin embargo, se ve un sorprendente vacío de concentración de galaxias visibles a lo largo de la materia oscura. Una respuesta hipotética es que la discrepancia causada por las grandes galaxias experimentan algún efecto de “tirachinas” gravitacional.
Una hipótesis más arriesgada sostiene que la materia oscura está chocándo consigo misma de alguna forma no gravitacional que nunca se había visto antes..? (esto está sacado de Observatorio y, en el texto que se ha podido traducir podemos ver que, los astrónomos autores de dichas observaciones, tienen, al menos, unas grandes lagunas en sus explicaciones y, tratándo de taparlas hacen aseveraciones que nada tienen que ver con la realidad).
emilio silvera
















 Totales: 83.321.188
Totales: 83.321.188 Conectados: 41
Conectados: 41