Jul
2
¡Una Singularidad! Extraño Objeto
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (10)
Comments (10)
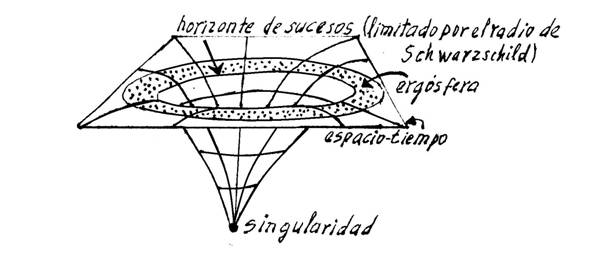

El concepto mismo de “singularidad” desagradaba a la mayoría de los físicos, pues la idea de una densidad infinita se alejaba de toda comprensión. La naturaleza humana está mejor condicionada a percibir situaciones que se caracterizan por su finitud, cosas que podemos medir y pesar, y que están alojadas dentro de unos límites concretos; serán más grande o más pequeñas pero, todo tiene un comienzo y un final pero… infinito, es difícil de digerir. Además, en la singularidad, según resulta de las ecuaciones, ni existe el tiempo ni existe el espacio. Parece que se tratara de otro universo dentro de nuestro universo toda la región afectada por la singularidad que, eso sí, afecta de manera real al entorno donde está situada y además, no es pacífica, ya que se nutre de cuerpos estelares circundantes que atrae y engulle.
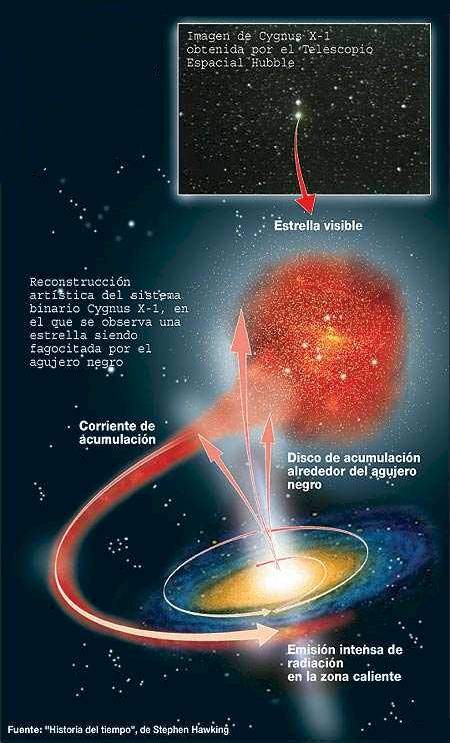
La noción de singularidad empezó a adquirir un mayor crédito cuando Robert Oppenheimer, junto a Hartlan S. Snyder, en el año 1.939 escribieron un artículo anexo de otro anterior de Oppenheimer sobre las estrellas de neutrones. En este último artículo, describió de manera magistral la conclusión de que una estrella con masa suficiente podía colapsarse bajo la acción de su propia gravedad hasta alcanzar un punto adimensional; con la demostración de las ecuaciones descritas en dicho artículo, la demostración quedó servida de forma irrefutable que una estrella lo suficientemente grande, llegado su final al consumir todo su combustible de fusión nuclear, continuaría comprimiéndose bajo su propia gravedad, más allá de los estados de enana blanca o de estrella de neutrones, para convertirse en una singularidad.

Los cálculos realizados por Oppenheimer y Snyder para la cantidad de masa que debía tener una estrella para terminar sus días como una singularidad estaban en los límites másicos de M =~ masa solar, estimación que fue corregida posteriormente por otros físicos teóricos que llegaron a la conclusión de que sólo sería posible que una estrella se transformara en singularidad, la que al abandonar su fase de gigante roja retiene una masa residual como menos de 2 – 3 masas solares.

La figura de la izquierda representa a la nube de polvo en colapso de Oppenhieimer y Snyder, que ilustra una superficie atrapada.
El modelo de Oppenhieimer y Snyder posee una superficie atrapada, que corresponde a una superficie cuya área se iOppenheimer y Snyder desarrollaron el primer ejemplo explícito de una solución a las ecuaciones de Einstein que describía de manera cierta a un agujero negro, al desarrollar el planteamiento de una nube de polvo colapsante. En su interior, existe una singularidad, pero no es visible desde el exterior, puesto que está rodeada de un horizonte de suceso que no deja que nadie se asome, la vea, y vuelva para contarlo. Lo que traspasa los límites del horizonte de sucesos, ha tomado el camino sin retorno. Su destino irreversible, la singularidad de la que pasará a formar parte.
Desde entonces, muchos han sido los físicos que se han especializado profundizando en las matemáticas relativas a los agujeros negros. John Wheeler (que los bautizó como agujeros negros), Roger Penrose, Stephen Hawking, Kip S. Thorne, Kerr y muchos otros nombres que ahora no recuerdo, han contribuido de manera muy notable al conocimiento de los agujeros negros, las cuestiones que de ellas se derivan y otras consecuencias de densidad, energía, gravedad, ondas gravitacionales, etc, que son deducidas a partir de estos fenómenos del cosmos.

Se afirma que las singularidades se encuentran rodeadas por un horizonte de sucesos, pero para un observador, en esencia, no puede ver nunca la singularidad desde el exterior. Específicamente implica que hay alguna región incapaz de enviar señales al infinito exterior. La limitación de esta región es el horizonte de sucesos, tras ella se encuentra atrapado el pasado y el infinito nulo futuro. Lo anterior nos hace distinguir que en esta frontera se deberían reunir las características siguientes:

- Debe ser una superficie nula donde es pareja, generada por geodésicas nulas;
- contiene una geodésica nula de futuro sin fin, que se origina a partir de cada punto en el que no es pareja, y que
- el área de secciones transversales espaciales jamás pueden disminuir a lo largo del tiempo.
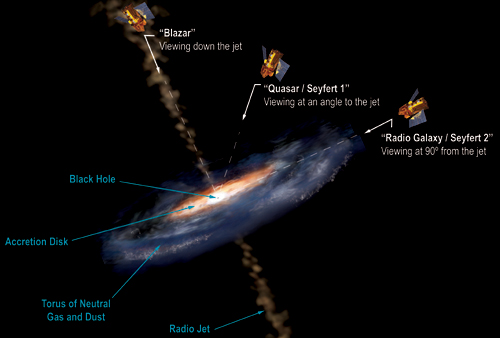
Pueden existir agujeros negros supermasivos (de 105 masas solares) en los centros de las galaxias activas. En el otro extremo, mini agujeros negros con un radio de 10-10 m y masas similares a las de un asteroide pudieron haberse formado en las condiciones extremas que se dieron poco después delBig Bang. Diminutos agujeros negros podrían ser capaces de capturar partículas a su alrededor, formando el equivalente gravitatorio de los átomos.

Todo esto ha sido demostrado matemáticamente por Israel, 1.967; Carter, 1.971; Robinson, 1.975; y Hawking, 1.978 con límite futuro asintótico de tal espaciotiempo como el espaciotiempo de Kerr, lo que resulta notable, pues la métrica de Kerr es una hermosa y exacta formulación para las ecuaciones de vacío de Einstein y, como un tema que se relaciona con la entropía en los agujeros negros.
No resulta arriesgado afirmar que existen variables en las formas de las singularidades que, según las formuladas por Oppenheimer y su colaborador Snyder, después las de Kerr y más tarde otros, todas podrían existir como un mismo objeto que se presenta en distintas formas o maneras.
Ahora bien, para que un ente, un objeto o un observador pueda introducirse dentro de una singularidad como un agujero negro, en cualquiera que fuese su forma, tendría que traspasar el radio de Schwarzschild (las fronteras matemáticas del horizonte de sucesos), cuya velocidad de escape es igual a la de la luz, aunque esta tampoco puede salir de allí una vez atrapada dentro de los límites fronterizos determinados por el radio. Este radio de Schwarzschild puede ser calculado usándose la ecuación para la velocidad de escape:

Para el caso de fotones u objeto sin masa, tales como neutrinos, se sustituye la velocidad de escape por la de la luz c2. “En el modelo de Schrödinger se abandona la concepción de los electrones como esferas diminutas con carga que giran en torno al núcleo, … Es cierto que en mecánica cuántica quedan muchos enigmas por resolver. Pero hablando de objetos de grandes masas, veámos lo que tenemos que hacer para escapar de ellos.
Podemos escapar de la fuerza de gravedad de un planeta pero, de un A.N., será imposible.
La velocidad de escape está referida a la velocidad mínima requerida para escapar de un campo gravitacional. El objeto que escapa puede ser cualquier cosa, desde una molécula de gas a una nave espacial. Como antes he reflejado está dada por , donde G es la constante gravitacional, M es la masa del cuerpo y R es la distancia del objeto que escapa del centro del cuerpo del que pretende escapar (del núcleo). Un objeto que se mueva a velocidad menor a la de escape entra en una órbita elíptica; si se mueve a una velocidad exactamente igual a la de escape, sigue una órbita parabólica, y si el objeto supera la velocidad de escape, se mueve en una trayectoria hiperbólica.
Así hemos comprendido que, a mayor masa del cuerpo del que se pretende escapar, mayor será la velocidad que necesitamos para escapar de él. Veamos algunas:
|
Objeto |
Velocidad de escape |
| La Tierra |
………….11,18 Km/s |
| El Sol |
………….617,3 Km/s |
| Júpiter |
………….59,6 Km/s |
| Saturno |
………….35,6 Km/s |
| Venus |
………….10,36 Km/s |
| Agujero negro |
…….+ de 299.000 Km/s |
Como se ve en el cuadro anterior, cada objeto celeste, en función de su masa, tiene su propia velocidad de escape para que cualquier cosa pueda salir de su órbita y escapar de él. El caso de la singularidad, es decir, la inmensa masa que está presente en las entrañas de un Agujero negro, genera una fuerza de gravedad tal que, nada está a salvo en sus inmediaciones, cualquier objeto, sea estrella, polvo estelar, planeta o lo que pudiera ser, será engullido por el “monstruo”, sin que nada pueda evitarlo.
La excepción está en el último ejemplo, la velocidad de escape necesaria para vencer la fuerza de atracción de un agujero negro que, siendo preciso superar la velocidad de la luz 299.792’458 Km/s, es algo que no está permitido, ya que todos sabemos que conforme determina la teoría de la relatividad especial de Einstein, la velocidad de la luz es la velocidad límite en nuestro universo; nada puede ir más rápido que la velocidad de la luz, entre otras razones porque el objeto sufriría la transformación de Lorentz y su masa sería infinita.
Podría continuar explicando otros aspectos que rodean a los agujeros negros, pero estimo que el objetivo que perseguía de hacer conocer lo que es un agujero negro y el origen del mismo, está sobradamente cumplido.
Existen aspectos del A.N. que influyen en el mundo cuántico, y, por ejemplo, el máximo radio que puede tener un agujero negro virtual está dado aproximadamente por
![]()
que equivale a unos 10-³³ centímetros. Esta distancia se conoce como longitud de Planck y es la única unidad de distancia que se puede construir con las tres constantes fundamentales de la naturaleza: G, h y c. La longitud de Planck es tan extremadamente pequeña (10²° veces menor que el radio de un electrón) que debe ser la distancia característica de otro nivel de la naturaleza, subyacente al mundo subatómico, donde rigen las leyes aún desconocidas de la gravedad cuántica.
Así como el océano presenta un aspecto liso e inmóvil cuando se observa desde una gran distancia, pero posee fuertes turbulencias y tormentas a escala humana, el espacio-tiempo parece “liso” y estático a gran escala, pero es extremadamente turbulento en el nivel de la longitud de Planck, donde los hoyos negros se forman y evaporan continuamente. En el mundo de Planck, las leyes de la física deben ser muy distintas de las que conocemos hasta ahora.
 La estructura macroscópica del espacio-tiempo parece plana, pero éste debe ser extremadamente turbulento en el nivel de la escala de Planck. Escala en la que parece que entramos en otro mundo… ¡El de la mecánica cuántica! que se aleja de ese mundo cotidinao que conocemos en el que lo macroscópico predomina por todas partes y lo infinitesimal no se deja ver con el ojo desnudo.
La estructura macroscópica del espacio-tiempo parece plana, pero éste debe ser extremadamente turbulento en el nivel de la escala de Planck. Escala en la que parece que entramos en otro mundo… ¡El de la mecánica cuántica! que se aleja de ese mundo cotidinao que conocemos en el que lo macroscópico predomina por todas partes y lo infinitesimal no se deja ver con el ojo desnudo.
¡Existen tántos secretos! ¡Es tan grande nuestra ignorancia!
emilio silvera
Jul
2
Las misteriosas funciones modulares
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Curiosidades ~
Clasificado en Curiosidades ~
 Comments (0)
Comments (0)
Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.
Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del Este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro Universo actual.
El misterio de las Funciones Modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él trabajó en total aislamiento, en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que, los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
La función modular de Ramanujan y la teoría de cuerdas
![]()
La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la … Pero hablemos de las cuerdas.
La teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.
No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre los más extraños jamás encontradas en matemáticas. Ellos reaparecen en los ramos más distantes e inconexos de las matemáticas. Una función, que aparece una y otra vez en la teoría de las funciones modulares, se denominan (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.
El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente, donde menos se esperan, por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. (Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio -tiempo debe tener 24 + 2 = 26 dimensiones espacio – temporales.)

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. No estará la solución final de la Teoría de cuerdas, en estas misteriosas funciones modelares.
Para comprender este misterioso factor de dos (que añaden los físicos consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.
Antes explicamos que cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio – tiempo sea diez.

Claro que, la Teoría de Cuerdas tiene versiones en 10, 11 y 26 dimensiones
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “No lo se”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por que se seleccionan estos números concretos.
Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.
Srinivasa Ramanujan nació en 1.887 en Erode, India, cerca de Madrás. Su familia de clase media alta, brahmin, la más alta de las castas Hindúes, fueron destituidos y venidos a menos, su padre trabajaba de oficinista de un comerciante de tejidos.
Con diez años, lo mismo que pasó antes con Riemann, ya destacaba y sorprendía a todos con sus enormes poderes de cálculos. Siendo niño, rederivó la identidad de Euler entre funciones trigonométricas y exponenciales.


En la vida de cada científico joven hay un punto de partida, un hecho que, sin ellos saberlo, les marca el destino. Para Einstein fue la fascinación que le causó la brújula que le regaló su tío cuando estaba enfermo siendo un niño, no podía apartar la mirada de la aguja que siempre indicaba hacia el mismo sitio, y se preguntó una y mil veces por la fuerza invisible que la obligaba a dirigirse hacia esa dirección. Para Riemann, fue la lectura del libro de matemáticas de Legendre. Para Ramanujan, fue cuando se sumergió en un oscuro y olvidado libro de matemáticas escrito por George Carr. Este libro ha quedado inmortalizado desde entonces por el hecho de que señaló la única exposición conocida de Ramanujan a los modernas matemáticas occidentales. Según su hermana: “Fue este libro el que despertó su genio. El se propuso establecer por sí mismo las fórmulas dadas allí. Como no tenía la ayuda de otros libros, cada solución era un trabajo de investigación por lo que a él concernía… Ramanujan solía decir que la diosa Namakkal le inspiraba las fórmulas en sueños”.

Con ayuda de amigos, Ramanujan consiguió un puesto de bajo nivel del puerto de Madrás. Era un trabajo servil, con una mísera paga de 20 libras al año, pero dio libertad a Ramanujan, como a Einstein antes que él en la oficina de Patentes Suiza, para seguir sus sueños en su tiempo libre. Ramanujan, en la fascinación que en él ejercían los números, era incansable, llenaba libretas enteras de cálculos y ecuaciones que antes veía florecer en su cabeza.
Así estaban las cosas cuando decidió escribir algunos de sus trabajos a las tres matemáticos más famosos de Inglaterra y Europa.
Dos de aquellos matemáticos, al tener en su poder las cartas enviadas por un miserable empleado sin instrucción formal alguna, sin haber comprobado su contenido, las arrojaron directamente a la basura. El tercero era el brillante matemático de Cambridge Godfrey Harold Hardy. Debido a su categoría en Inglaterra, Hardy estaba acostumbrado a recibir correo de chiflados proponiéndole los más peregrinos proyectos y, en un primer momento apenas prestó atención a la carta del joven Ramanujan.
Srinivasa Ramanujan trabajó principalmente en teoría de números, encontrando identidades relacionadas con el número pi y el número e o los números primos. Como decimos, en general sus fórmulas son muy enrevesadas, pero en su mayoría verdaderas (a posteriori se ha descubierto que algunos de sus resultados era incorrectos), y algunas de ellas se han convertido en potentes herramientas para calcular grandes cantidades de decimales de, principalmente, el número pi. Quizás la más conocida sea ésta:
que nos da 8 decimales exactos de pi en cada iteración. Tremendo, ¿verdad?
Entre los densos garabatos advirtió muchos teoremas matemáticos que ya eran bien conocidos. Pensando que era la obra obvia de un plagiario, el también la desechó en ese primer impulso. Pero había algo que no encajaba. Algo que inquietaba a Hardy; no podía dejar de pensar en aquella extraña carta.
Durante la cena de esa noche, 16 de enero de. 1913, Hardy y su colega John Littlewood discutieron esta carta singular y decidieron echar un segundo vistazo – repaso a su contenido. Comenzaba de forma bastante inocente, con “Me permito presentarme a usted como un empleado en el departamento de contabilidad de la oficina del puerto franco de Madrás con un salario de solo veinte libras al año”. Pero la carta del pobre empleado de Madrás contenía teoremas que eran totalmente desconocidos para los matemáticos occidentales. En total, contenía 120 teoremas. Hardy estaba atónito. Recordaba que demostrar algunos de esos teoremas “Me derrotó por completo”. “Nunca había visto nada antes que se le pareciera en lo más mínimo. Una simple ojeada a ellos es suficiente para mostrar que sólo podían estar elaborados por un matemático muy grande”.
Littlewood y Hardy alcanzaron la misma conclusión: Aquello era el trabajo de un genio empeñado en derivar de nuevo 100 años de matemáticas europeas. “Él había estado llevando a cabo una carrera imposible, un pobre y solitario hindú, completamente solo y sin ayuda, enfrentando su cerebro contra toda la sabiduría acumulada en Europa”, recordaba con asombro Hardy.

Hardy escribió a Ramanujan y, tras muchas pesquisas, uso de amistades e influencias, arregló su estancia en Cambridge en 1.914. Por primera vez, Ramanujan podía comunicarse regularmente con sus iguales, la comunidad de los matemáticos europeos. Entonces comenzó el estallido de su actividad: tres cortos e intensos años de colaboración con Hardy en el Trinity Collage en Cambridge.
Hardy trató más tarde de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido como uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando este diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló: “Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi número 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y también la suma de 9 x 9 x 9 y 10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el nombre de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Si finalmente las dos madejas se desenredan… ¡Por algo será!
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.
En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas. Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión. El enunciado correcto sería ahora: las leyes de la naturaleza se simplifican cuando se expresan COHERENTEMENTE en dimensiones más altas. El añadido de la palabra coherente es crucial. Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo. Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.
Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.
¿La décima dimensión?
¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?
Steven Weinberg
emilio silvera
El apunte sobre Ramanujan fue incluido en otro de mis trabajos. Sin embargo, el presente cuaderno trata temas expresamente solicitados para utilizar en unos seminarios de física, y se me pidió incluir el tema “Ramanujan”. La Fuente es diversa y precisaría una larga relación.















 Totales: 75.528.565
Totales: 75.528.565 Conectados: 41
Conectados: 41






















