¡Interacciones fundamentales!

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.

Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del Este.  Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro Universo actual.

El misterio de las Funciones Modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos.  Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él trabajó en total aislamiento, en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que, los buscó sin conocerlos.  Perdió muchos años de su vida en redescubrir matemáticas conocidas.

La función modular de Ramanujan y la teoría de cuerdas

La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la … Pero hablemos de las cuerdas.

La teoría de cuerdas  supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.

No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares,  que figuran entre los más extraños jamás encontradas en matemáticas.   Ellos reaparecen en los ramos más distantes e inconexos de las matemáticas.  Una función, que aparece una y otra vez en la teoría de las funciones modulares, se denominan (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor.  Esta extraña función contiene un término elevado a la potencia veinticuatro.

El número 24 aparece repetidamente en la obra de Ramanujan.  Este es un ejemplo de lo que las matemáticas llaman números mágicos,  que aparecen continuamente, donde menos se esperan, por razones que nadie entiende.   Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas.   El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas.  En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda.  Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas.   Estas son precisamente las entidades matemáticas descubiertas por Ramanujan.  (Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio -tiempo debe tener 24 + 2 = 26 dimensiones espacio – temporales.)

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. No estará la solución final de la Teoría de cuerdas, en estas misteriosas funciones modelares.

Para comprender este misterioso factor de dos (que añaden los físicos consideramos un rayo de luz que tiene dos modos físicos de vibración.  La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente.  Sin embargo, un campo de Maxwell relativista A_µ tiene cuatro componentes, donde _{µ =} 1, 2, 3, 4.  Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell.  Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos.  Análogamente, una cuerda relativista vibra en 26 dimensiones.  Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Antes explicamos que cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8.   Por lo tanto, el número crítico para la supercuerda es 8+2=10.  Este es el origen de la décima dimensión que exige la teoría.   La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente.  Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda.   Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende.  Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio – tiempo sea diez.

               Claro que, la Teoría de Cuerdas tiene versiones en 10, 11 y 26 dimensiones

En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan.  Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “No lo se”.  Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por que se seleccionan estos números concretos.

Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.

Srinivasa Ramanujan nació en 1.887 en Erode, India, cerca de Madrás.  Su familia de clase media alta, brahmin, la más alta de las castas Hindúes, fueron destituidos y venidos a menos, su padre trabajaba de oficinista de un comerciante de tejidos.

Con diez años, lo mismo que pasó antes con Riemann, ya destacaba y sorprendía a todos con sus enormes poderes de cálculos.   Siendo niño, rederivó la identidad de Euler entre funciones trigonométricas y exponenciales.

En la vida de cada científico joven hay un punto de partida, un hecho que, sin ellos saberlo, les marca el destino.  Para Einstein fue la fascinación que le causó la brújula que le regaló su tío cuando estaba enfermo siendo un niño, no podía apartar la mirada de la aguja que siempre indicaba hacia el mismo sitio, y se preguntó una y mil veces por la fuerza invisible que la obligaba a dirigirse hacia esa dirección. Para Riemann, fue la lectura del libro de matemáticas de Legendre.  Para Ramanujan, fue cuando se sumergió en un oscuro y olvidado libro de matemáticas escrito por George Carr.   Este libro ha quedado inmortalizado desde entonces por el hecho de que señaló la única exposición conocida de Ramanujan a los modernas matemáticas occidentales.   Según su hermana: “Fue este libro el que despertó su genio.  El se propuso establecer por sí mismo las fórmulas dadas allí.  Como no tenía la ayuda de otros libros, cada solución era un trabajo de investigación por lo que a él concernía…  Ramanujan solía decir que la diosa Namakkal le inspiraba las fórmulas en sueños”.

Con ayuda de amigos, Ramanujan consiguió un puesto de bajo nivel del puerto de Madrás.   Era un trabajo servil, con una mísera paga de 20 libras al año, pero dio libertad a Ramanujan, como a Einstein antes que él en la oficina de Patentes Suiza, para seguir sus sueños en su tiempo libre.   Ramanujan, en la fascinación que en él ejercían los números, era incansable, llenaba libretas enteras de cálculos y ecuaciones que antes veía florecer en su cabeza.

Así estaban las cosas cuando decidió escribir algunos de sus trabajos a las tres matemáticos más famosos de Inglaterra y Europa.

Dos de aquellos matemáticos, al tener en su poder las cartas enviadas por un miserable empleado sin instrucción formal alguna, sin haber comprobado su contenido, las arrojaron directamente a la basura.   El tercero era el brillante matemático de Cambridge Godfrey Harold Hardy. Debido a su categoría en Inglaterra, Hardy estaba acostumbrado a recibir correo de chiflados proponiéndole los más peregrinos proyectos y, en un primer momento apenas prestó atención a la carta del joven Ramanujan.

Srinivasa Ramanujan trabajó principalmente en teoría de números, encontrando identidades relacionadas con el número pi y el número e o los números primos. Como decimos, en general sus fórmulas son muy enrevesadas, pero en su mayoría verdaderas (a posteriori se ha descubierto que algunos de sus resultados era incorrectos), y algunas de ellas se han convertido en potentes herramientas para calcular grandes cantidades de decimales de, principalmente, el número pi. Quizás la más conocida sea ésta:

que nos da 8 decimales exactos de pi en cada iteración. Tremendo, ¿verdad?

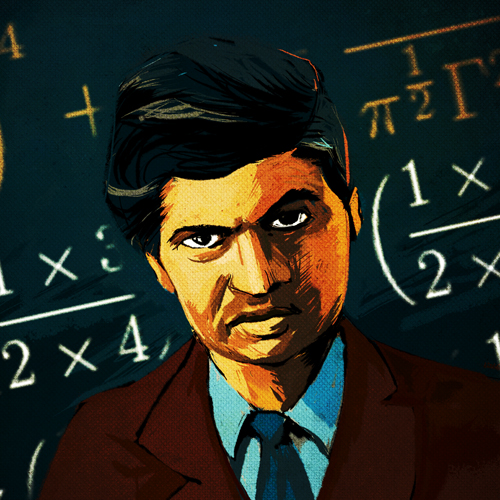
Entre los densos garabatos advirtió muchos teoremas matemáticos que ya eran bien conocidos.  Pensando que era la obra obvia de un plagiario, el también la desechó en ese primer impulso.   Pero había algo que no encajaba.  Algo que inquietaba a Hardy; no podía dejar de pensar en aquella extraña carta.

Durante la cena de esa noche, 16 de enero de. 1913, Hardy y su colega John Littlewood discutieron esta carta singular y decidieron echar un segundo vistazo – repaso a su contenido.   Comenzaba de forma bastante inocente, con “Me permito presentarme a usted como un empleado en el departamento de contabilidad de la oficina del puerto franco de Madrás con un salario de solo veinte libras al año”.   Pero la carta del pobre empleado de Madrás contenía teoremas que eran totalmente desconocidos para los matemáticos occidentales.  En total, contenía 120 teoremas.  Hardy estaba atónito.  Recordaba que demostrar algunos de esos teoremas “Me derrotó por completo”.  “Nunca había visto nada antes que se le pareciera en lo más mínimo.   Una simple ojeada a ellos es suficiente para mostrar que sólo podían estar elaborados por un matemático muy grande”.

Littlewood y Hardy alcanzaron la misma conclusión: Aquello era el trabajo de un genio empeñado en derivar de nuevo 100 años de matemáticas europeas. “Él había estado llevando a cabo una carrera imposible, un pobre y solitario hindú, completamente solo y sin ayuda, enfrentando su cerebro contra toda la sabiduría acumulada en Europa”, recordaba con asombro Hardy.

Hardy escribió a Ramanujan y, tras muchas pesquisas, uso de amistades e influencias, arregló su estancia en Cambridge en 1.914.  Por primera vez, Ramanujan podía comunicarse regularmente con sus iguales, la comunidad de los matemáticos europeos.  Entonces comenzó el estallido de su actividad: tres cortos e intensos años de colaboración con Hardy en el Trinity Collage en Cambridge.

Hardy trató más tarde de estimar la capacidad matemática que poseía Ramanujan.   Concedió a David Hilbert, universalmente conocido y reconocido como uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80.   A Ramanujan le asignó una puntuación de 100.  Así mismo, Hardy se concedió un 25.

Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando este diluvio material brotaba de sus sueños con semejante frecuencia.   Hardy señaló: “Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.

Hardy recordaba vivamente:

-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney.  Yo había tomado el taxi número 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”

– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.

 

(Es la suma de 1 x 1 x 1  y 12 x 12 x 12, y también la suma de 9 x 9 x 9  y  10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.

En 1.919 volvió a casa, en la India, donde un año más tarde murió  enfermo.

El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración.  En 1.976, sin embargo, se hizo un nuevo descubrimiento.   Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage.   Esto se conoce ahora con el nombre de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:

“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”.  Lo que él consiguió era increíble.  Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.

 

Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna,   la única capaz de unir la mecánica quántica y la Gravedad.

Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie.   Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro.   Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.

                         Si finalmente las dos madejas se desenredan… ¡Por algo será!

Como saben los físicos, los “accidentes” no aparecen sin ninguna razón.  Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente.  Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego.  Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Aquí es precisamente donde entra el trabajo de Ramanujan.  Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan.  ¡Increíble!   Pero, cierto.

En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas.   Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión.   El enunciado correcto sería ahora:   las leyes de la naturaleza se simplifican cuando se expresan  COHERENTEMENTE en dimensiones más altas.  El añadido de la palabra coherente es crucial.   Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo.   Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.

Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil.  Cualquier teoría, afirman, debe ser verificable.   Puesto que ninguna teoría definida a la energía de Planck de 10¹⁹ miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría!

El principal problema, es teórico más que experimental.  Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría.  Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

¿La décima dimensión?

¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?

Steven Weinberg

 

emilio silvera

El apunte sobre Ramanujan fue incluido en otro de mis trabajos.  Sin embargo, el presente cuaderno trata temas expresamente solicitados para utilizar en unos seminarios de física, y se me pidió incluir el tema “Ramanujan”. La Fuente es diversa y precisaría una larga relación.

  ¿El futuro de Marte? Hasta podría ser nuestra nueva casa.

Desde los confines del Tiempo, cuando aún no entendíamos lo que todo aquello podría ser, los seres de nuestra especie han mirado al cielo y, asombrados, contemplaban las miríadas de estrellas brillantes que, con sus guiños, parecía quererles decir alguna cosa, enviarles un mensaje que, por aquel entonces, no sabían comprender. No ha sido sino hasta tiempos muy recientes cuando al fín, comprendimos la fusión nuclear que se produce en el corazón de las estrellas, donde se forjan los materiales necesarios para la vida.

Uno de los hallazgos más notables en astronomía fue el descubrimiento de que el universo ya era viejo cuando apareció el Sol y la familia de planetas que lo acompañan en nuestro Sistema Solar. Más de la mitad de las estrellas del Universo son miles de millones de años más viejas que nuestra estrella madre que, se podría decir, si la comparamos a una bella mujer, que estaría en la mitad esplendorosa de su vida.

Planetas parecidos a la Tierra giran alrededor de muchas de esas viejas estrellas. Seres inteligentes pueden haber hecho su aparición en alguno de esos mundos similares al nuestro y estar allí desde mil millones de años antes que nosotros en la Tierra. Es decir, antes de que la Humanidad hiciera acto de presencia en este mundo “nuestro”. Los caminos seguidos en ambos mundos, aunque similares en las formas, no lo fueron en el tiempo y, en aquel, brotó la vida antes que en este. Una posible civilización avanzada que nos podría llevar algunos miles de años de ventaja, tiempo que para una especie parecida a la nuestra… ¡no sería poca ventaja!

Gliese 581 f es un planeta en la constelación de Libra, ubicado a 20 años luz de la Tierra, en el sistema Gliese 581. Su descubrimiento fue anunciado el 29 de septiembre de 2010. El planeta fue detectado mediante mediciones de la velocidad radial combinando los datos del instrumento HIRES  del telescopio Keck  y el instrumento HARPS  del telescopio de 3,6 metros dE ESO en el Observatorio de La Silla.

Muchos son los Sistmas solares que sólo en nuestra Galaxia podremos encontrar, en realidad, cientos de miles de millones y, aunque no todos esten habitados, la posibilidad, la lógica, la estadísitica nos dice que, muchos de esos mundos, cobijan a criaturas de diversa condición y, alguna -o varias- de las especies allí presentes, podr´na ser inteligentes como nosotros…, o más.

Como nos preocupa saber que existe a nuestro alrededor, qué hay en nuestro entorno, en los planetas y lunas vecinas, no cejamos en el empeño de enviar ingenios hacia aquellos objetos y, el de arriba se llama JEO (Jupiter Europa Orbiter) que, debía estudiar Europa durante la próxima década para determinar de una vez por todas si existe un océano (o lagos) bajo la corteza de hielo y, con suerte, aclarar si puede existir o no alguna forma de vida. Sin embargo, la crisis que nos invade, no parece que posibilite, al menos de momento, tal misión.

En lo que se refiere a las formas de vida que nos podemos encontrar por ahí fuera, nuestra imaginación ha sido muy prolífica y nos ha diseñado un sin fin de formas de vida que, están diseñadas de todas las maneras que podamos imaginar, desde los hombres reptiles inteligentes hasta los hombrecillos verdes. Tampoco hemos dejado pasar la oportunidad de mostrar en películas y obras de ciencia ficción, a seres monstruosos con las morfologías más descabelladas y las figuras más temibles y horripilantes.

Claro que, tenemos que pensar que, aquí en nuestro mundo, todas las especies que conocemos y que han existido, todas sin excepción, han estado y están basadas en el Carbono, y, si eso es así (que lo es), habría que pensar en el hecho cierto de que, el Universo, es igual en todas partes, y, las mismas cosas que pasan aquí tienen que suceder “allí”, y, salvo las condiciones físicas de cada lugar, es lógico pensar en el hecho de que, la Vida, como aquí en la Tierra, habrá tomado las formas que cada lugar y entorno requerieran.

       Algunos dicen que somos nosotros en el futuro

Los conocidos como grises, esa raza que dicen que vienen del futuro pero que somos nosotros mismos evolucionados. La rumorología en ciertos ambiente. Los grises, también llamados los extraterrestres de Roswell y Zetas Reticulianos, son unas de las supuestas distintas formas de vida extraterrestre más famosas y actualmente “conocidas” que aparecen en las modernas teorías de conspiración del ocultamiento extraterrestre.

Particularmente creo que, lo mismo que nosotros, esos posibles seres del Espacio exterior, habitantes de otros mundos, se han encontrado las mismas dificultades que nosotros: ¡Las Inmensas Distancias! A veces pienso que, el Universo es consciente de que, si no fuese por esas inconmensurables distnacias entre las estrellas y los mundos, estaríamos todo el tiempo fustigando a los vecinos, y, sólo de ésta manera se puede conseguir mantenernos separados y sin que los unos molestémos a los otros. Sólo tenemos que fijarnos en la convivencia aquí mismo, en el planeta Tierra, donde todo el día andamos pensando como fastidiar al otro. ¡La Humanidad! No tenemos remedio.

                                       El bueno de YODA

La imagen de arriba me resulta familiar y creíble para unos posibles pobladores de otro mundo avanzado con tecnología de mucho kilates. Estos hombrecillos conformados de manera tal que, es el cerecro lo que predomina en el conjunto, nos viene a dar la sensación de que pudiera ser nuestro lejano futuro en el que, el cerebro crecerá tal como la ha venido haciendo en los tiempos pasados en que los, los humanos sólo tenían 450 cm³ de masa encefálica y ahora, hemos alcanzado 1.500 cm³ que se traducen enlos conocimientos que nos adornan hoy.

Cuando la evolución está en marcha, los que menos la “sienten” son lo que afectados por ella, ya que, al ser parte integrante del suceso, de la transformación de fase, la “cosa”, puede pasar, casi desapercibida a no ser que exista un sistema continuado de vigilancia sobre ello. Fijáos, por ejemplo en el ritmo de los nuevos inventos durante los últimos cien años:

A todos eso añadimos las nuevas y potentes computadoras, nuevas medicinas, radio, ingenios espaciales… Cada uno de ellos viene a darle al anterior un toque mágico que le hace más asombroso y ofrece más prestaciones al usuario, con todos ellos, la vida humana es más fácil, más confortable, más cercana. En realidad, si miramos la Historia, estamos contemplando un desarrollo acelerado que, aunque nuestros ojos no parece que se deje sentir, en realidad, el salto dado es descomunal y, lo que se nos viene encima antes de que finalice el presente siglo… será también asombroso.

La nave Flammarion I, que llegó al planeta Isatet 137, situado en la galaxia Rímola, a 23 años-luz de la Tierra, pudo tomar tierra sin problemas cerca de unas instalaciones de majestuosa presencia y, un equipo de exploración del terreno, habiéndose introducidos con precaución en el interior de aquel bello edificio, encontraron, en una de sus salas, una Cámara de Éxtasis en la que una mujer de edad avanzada, permanecia quieta, como dormida.

La Noticia fue comunicada al mando en la Nave y, de inmediato, un equipo de expertos médicos salieron con una lanzadera hacia el lugar para tratar de despertar a la dama y que ella, les contara a qué situación se podían enfrentar y dónde estaban y quiénes eran ellos, su raza que, por todas las trazas físicas, parecían iguales a los habitantes de la Tierra.

Estas dos serie de Televisión, refleja bastante bien lo que podría ser el futuro, refleja cuestiones de ciencia, de viajes hiperespaciales y por agujeros de gusano que, ¿quién sabe? si en el futuro próximo no esará todo eso a nuestro alcance. Acodémonos de Julio Verne que, a sus coetáneos les parecía un alucinado vidente que no todos llegaron a creer y…sin embargo, todo lo que dijo ha sido ya…, ¡sobrepasado!

Claro que, la Naturaleza, el Universo, nos impone sus leyes que impiden que “no nos hagamos daño” nosotros mismos, en nuestro empeño de querer llegar más allá de lo que es conveniente. Todo tiene que ser en su momento adecuado. Así, aunque la presentimos y, posiblemente, esté ahí, la Teoría de Cuerdas no será un hecho hasta dentro de mucho, mucho tiempo, cuando podamos disponer -sin peligro- de energías que son hoy impensables.

Es visible a simple vista que, nuestras actuales naves espaciales son -guardando las distancias- como aquellas carretas del Oeste americano que salían a explorar nuevos caminos y conquistar nuevas tierras sin saber qué peligros tendrían que afrontar. Sin embargo, no pasarán muchas décadas antes de que, la Humanidad, pueda construir naves de increíble porte y sofisticados instrumentos que, esas sí, podrán surcar los océanos espaciales a velocidades alucinantes como un primer paso para lo que más tarde vendrá.

La Humanidad no puede permanecer ajena a la realidad del mundo y, el tiempo pasa, las generaciones se van y llegan otras nuevas, las Sociedades avanzar y se transforman y, la población crece. ¿Cuántos miles de millones de seres seremos en el planeta para dentro de 5 siglos? ¿Cómo podremos suministrar todo lo que esa ingente cantidad de personas necesitan? El planeta Tierra tiene recurso limitados y, llegará un momento en el que no pueda suministrar ni la energía ni el alimento y, nos veremos abocados a buscar, otras opciones que, sin duda, pasan por salir fuera, a otros mundos lejos de este.

La Imaginación humana siempre ha sido grande, muy grande y creo que, hasta ilimitada a medida que la mente evoluciona. Todo lo que imagina… se podría convertir en realidad y, habiendo pensado ya en el Hiperespacio… Creo que sólo tendremos que buscar esa puerta que nos lleve lejos de aquí en menos tiempo. No podemos vencer a la velocidad de la Luz, el límite impuesto por la Naturaleza no lo permite y, podría ser, que ese límite esté impuesto por alguna razón:

¿Cuanto tardaríamos, suponiendo que pudiéramos hacer naves viajeras que alcazaran la mitad de la velocidad de la luz, en llegar a Planetas situados a muchos años-luz de aquí? El viaje sería interminable y la nave, tendría que ser una ciudad flotante que soportaria el paso de varias generaciones durante el viaje. Así que, como dicho sistema no parece muy viable, la Naturaleza nos empuja a tener que buscar otros caminos que, como el Hiperespacio y los Agujeros de Gusano, podrían ser una solución ideal para nuestras necesidades futuras.

Lo que llamamos Hiperespacio podría ser un aspecto del universo muy concreto que es experimentado por objetos que se desplazan a una velocidad superior a la luz relativa del fondo galáctico. Es una dimensión del espacio-tiempo que permite una velocidad superior a la de la luz y viajar a través de él elimina los efectos distorsionantes del tiempo derivados de la relatividad. Un viajero hiperespacial pasa tanto rato viajando como tiempo corre en el espacio real. Es una dimensión paralela al espacio real y cada punto de este está asociado con un punto único del hiperespacio y por consiguiente los puntos adyacentes en el espacio real son también adyacentes en el hiperespacio.

La idea básica de lo que es el viaje a travez del hiperespacio puede comprenderse tomando una hoja de papel y marcando en ella dos puntos relativamente alejados. La forma más rápida de viajar entre ellos es coger una regla y dibujar una línea recta que los una. Sin embargo, si nos fuera dado hacer trampas, cogeríamos la hoja de papel y la doblaríamos, uniendo directamente los dos puntos, reduciendo así a cero su distancia y haciendo el viaje instantáneo.

Si conseguimos eso algún día lejano en el futuro, podremos viajar a otros mundos lejanos situados en la nuestra o en otras galaxias, entablar amistad y comercio con otras Civilizaciones y hacer del Universo, lo que muchas veces hemos pensado: Un Todo para Todos en armonía y Paz.

Bueno, una alta capacidad de conocimiento nos llevaría a comprender que, las disputas y guerras, finalmente no conducen nada más que a la muerte y a la destrucción, que lo que realmente vale son otros valores, otras cosas, otros sentimientos y, siendo así (que lo es), esperémos que, algún día lejos aún en el futuro, por fin podamos decir, no ya en relación a la Tierra, sino en relación a todo el Universo que, todos somos uno.

Sí, un verdadero amigo…”un hermano”, lo podemos encontrar en cualquier parte, hasta en un mundo lejano y diferente al nuestro. Las inteligencias se unen para poder vencer las dificultades que acechan y, el esfuerzo conjunto puede vencer la adversidad. Los sentimientos, los pensamientos y las ideas, cuando la inteligencia está presente, recorrerá los mismos caminos.

Poco importaran las diferencias y, dentro de la desigualdad, también llegará la amistad y el cariño. Lo que en verdad nos une es el comprender que todo, absolutamente todo, es igual y lo mismo en todas partes que, sin importar las formas ni los colores, hará prevalecer los pensamientos y los sentimientos que, al fin y al cabo… ¡Es lo más valioso que en el Universo existe!

                     ¿Qué importa el mundo o el lugar si, allí se encuentra ella?

¿hasta donde serías capaz de viajar en busca del ser amado? ¿Qué peligros estarías dispuesto a pasar por ella? Hay preguntas que, si en verdad sentimos ese verdadero sentimiento que nos eleva y nos hace mejores, tienen de antemano las respuestas: Nada nos podrá parar, ningún peliqro, ningún viaje, ninguna dificultad… Todo, absolutamente todo, nos parecerá trivial si, al final, está ella esperando. De la misma manera, podemos sentir cuando se trata de viajar a nuestro futuro, a esos mundos soñados, a esas vidas nuevas, a fantásticos lugares que, fuera y lejos de este nuestro, también están ahí fuera como una promesa.

   No debemos olvidar la primera fuerza que mueve el mundo

Es el Amor energía,

O torbellino de un momento,

Es una sensación de alegría,

Es el mayor sentimiento.

Hasta el mundo nos queda pequeño,

Ante inmensa sensación,

Es el Amor un empeño,

¿Es el Amor la sinrazón?

Bueno, eso que arriba brilla, no es ninguna estrella fulgurante, es mi amada que, al recibir el mensaje de Amor, de inmediato se convierte, en un este deslumbrador. El Amor cambia el aspecto, el talente y, si me apuráis mucho, hasta el intelecto. ¿Qué podrá ser esa dichosa sensación? ¡Sabia Naturaleza! Cuando todo el Universo esté lleno de ese Ingrediente… ¡Las cosas serán de otra manera!

emilio silvera

No, Kepler-452b no es el planeta más parecido a la Tierra hallado hasta ahora

La NASA y el SETI dan a conocer el nuevo catálogo de 500 posibles exoplanetas, entre los que se encuentra Kepler-452b. ¿Es cierto que se parece a la Tierra?