Todos hemos oído hablar, con más o menos frecuencia, de “Sistemas Complejos”, aquí mismo en estas páginas, la palabra sale a relucir con cierta frecuencia y, no me extraña que “la palabreja” cree una barrera, dado que, que para muchas personas, “complejo” significa “complicado” y suponen automáticamente que, si un sistema es complicado, será difícil de comprender. La naturaleza posee una fuerte tendencia a estructurarse en forma de entes discretos excitables que interactúan y que se organizan en niveles jerárquicos de creciente complejidad, por ello, los sistemas complejos no son de ninguna manera casos raros ni curiosidades sino que dominan la estructura y función del universo.

Claro que, no siempre ese temor a lo difícil y complicado, está justificado y, tal suposición no es, necesariamente correcta. En realidad, un sistema complejo es tan solo un sistema que está formado por varios componentes más sencillos que ejercem entre sí una interacción mutua que, naturalmente, tiene sus consecuencias. Si miramos la imagen de arriba, vemos una inmensa y hermosa Nebulosa que está formada por una serie de “cosas” sencillas como lo son el gas hidrógeno y el polvo interestelar entre otros y, en presencia de energías, la gravedad y otros parámetros, ahí ocurren cosas tales como, el nacimiento de estrellas y la aparición de mundos…entre otras.

Los grandes triunfos de la Ciencia se han logrado, en gran medida, descomponiendo los sistemas complejos en sus componentes simples, es decir, estudiar por partes lo que allí está presente (en caso necesario, como primera aproximación, dando el paso suplementario de pretender que todos los componentes son más sencillos de lo que son en realidad) para llegar a comprender el todo.

En el ejemplo clásico del éxito que ha logrado este planteamiento para conocer el mundo que nos rodea, buena parte de la química puede entenderse mediante un modelo en el que los componentes simples son átomos, y para eso importa poco de qué están formados los núcleos. Ascendiendo un nivel, las leyes que describen el comportamiento del dióxido de Carbono encerrado en una caja pueden entenderse pensando en unas moléculas más o menos esféricas que rebotan unas contra otras y contra las paredes de su contenerdor, y poco importa que cada una de estas moléculas esté formada por un átomo de Carbono y dos de Oxígeno unidos entre sí. Ambos sistemas son complejos, en sentido científico, pero fáciles de entender

A veces en la vida nuestro mundo se oscurece, todo lo que nos rodea es dudoso y retorcido, oímos pasos que nos siguen, siempre han estado ahí, … No sabemos a quién pueden pertenecer y, a nuestro alrededor hay cosas que no podemos ver.

No siempre sabemos ver el mundo que nos rodea. El que miremos no significa que estemos viendo lo que realmente hay delante de nuestros ojos y, muchas veces, no son los ojos los únicos que pueden “ver” lo que hay más allá de lo que la vista puede alcanzar. Anoche, hasta una hora avanzada, estuve releyendo el Libro “Así de Simple” de John Gribbin, y, pareciéndome interesante os saqué un pequeño resumen del comienzo. Aquí os lo dejo.

El mundo que nos rodea parece ser un lugar complicado. Aunque hay algunas verdades sencillas que parecen eternas (las manzanas caen siempre hacia el suelo y no hacia el cielo; el Sol se levanta por el este, nunca por el oeste), nuestras vidas, a pesar de las modernas tecnologías, están todavía, con demasiada frecuencia, a merced de los complicados procesos que producen cambios drásticos y repentinos. La predicción del tiempo atmosférico tiene todavía más de arte adivinatorio que de ciencia; los terremotos y las erupciones volcánicas se producen de manera impredecible y aparentemente aleatorias; las fluctuaciones de la economía siguen ocasionando la bancarrota de muchos y la fortuna de unos pocos.

                                              Sobre la posición de la salida del Sol

Desde la época de Galileo (más o menos, a comienzos del siglo XVII) la ciencia ha hecho progresos –enormes-, ignorando en gran medida estas complejidades y centrándose en cuestiones sencillas, intentando explicar por qué las manzanas caen al suelo y por qué el Sol se levanta por el este. Los avances fueron de hecho tan espectaculares que hacia mediados del siglo XX ya se había dado respuesta a todas las cuestiones sencillas. Conceptos tales como la teoría general de la relatividad y la mecánica cuántica explicaron el funcionamiento global del universo a escalas muy grandes y muy pequeñas respectivamente, mientras el descubrimiento de la estructura del ADN y el modo en que éste se copia de una generación a otra hizo que la propia vida, así como la evolución, parecieran sencillas a nivel molecular. Sin embargo, persistió la complejidad del mundo a nivel humano –al nivel de la vida-. La cuestión más interesante de todas, la que planteaba cómo la vida pudo haber surgido a partir de la materia inerte, siguió sin respuesta.

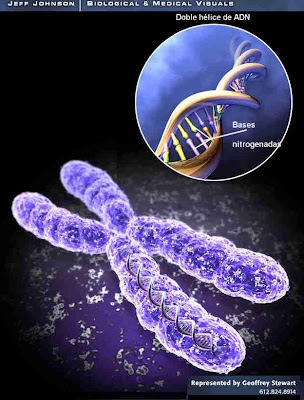
Un descubrimiento así no podía dejar al mundo indiferente. En unos años el mundo científico se puso al día y la revolución genética cambió los paradigmas establecidos. Mucha gente aún no está preparada para aceptar el comienzo de una era poderosa en la que el ser humano tiene un control de sí mismo mayor al habitual. Había nacido la Ingeniería genética.

No debe extrañarnos que sea precisamente a escala humana donde se den las características más complejas del universo. Las que se resisten más a rendirse ante los métodos tradicionales de la investigación científica. Realmente, es posible que seamos lo más complejo que existe en el universo. La razón es que, a escalas más reducidas, entidades tales como los átomos se comportan individualmente de un modo relativamente sencillo en sus interacciones mutuas, y que las cosas complicadas e interesantes surgen, cuando se unen muchos átomos de maneras complicadas e interesantes, para formar organismos tales como los seres humanos.

   ¿Que pensamientos rondaran por esa cabecita?

Pero este proceso no puede continuar indefinidamente, ya que, si se unen cada vez más átomos, su masa total aumenta hasta tal punto que la Gravedad aplasta toda la estructura importante y la aniquila. Un átomo, o incluso una molécula tan simple como la del agua, es algo más sencillo que un ser humano, porque tiene poca estructura interna; una estrella, o el interior de un planeta, es también algo más sencillo que un ser humano porque la gravedad aplasta cualquier estructura hasta aniquilarla. Esta es la razón por la cual la ciencia puede decirnos más sobre el comportamiento de los átomos y el funcionamiento interno de las estrellas o los planetas que sobre el modo en que las personas nos comportamos.

Sí, hemos podido llegar a conocer lo que ocurre en el Sol, y sabemos de sus procesos interiores y exteriores, de las ráfagas de partículas que en sus épocas activas, nos envía continuamente hacía la superficie del planeta y, que no sólo provoca esas bonitas Auroras, sino que, su intensa radiación y magnetismo incide en todos los atilugios que tenemos para leer los datos de… ¡tántas cosas!

Cuando los problemas sencillos se rindieron ante el empuje de la investigación, fue algo natural que los científicos abordaran rompecabezas más complicados que iban asociados con sistemas complejos, para que por fin fuera posible comenzar a comprender el funcionamiento del mundo a una escala más humana compleja y, para ello, hubo que esperar hasta la década de 1960, que fue cuando aparecieron los poderosos y rápidos (para lo que se estilaba en aquella época) ordenadores electrónicos. Estos nuevos inventos empezaron a ser conocidos por un público más amplio entre mediados y finales de la década de 1980, primero con la publicación del libro, ahora convertido en un clásico, Order out of Chaos, de Ilya Prigogine e Isabelle Stergers, y luego, con Chaos, de James Gleick.

Las personas sencillas que, aunque tengan una educación aceptable, no están inmersas en el ámbito de la ciencia, cuando oyen hablar de Complejidad y Caos en esas áreas, sienten, de primeras, una especie de rechazo por aquello que (ellos creen) no van a comprender. Sin embargo, la cuestión no es tan difícil como a primera vista pudiera parecer, todo consiste en tener la posibilidad de que alguien, de manera “sencilla” (dentro de lo posible), nos explique las cosas dejando a un lado las matemáticas que, aunque describen de manera más amplia y pura aquellos conceptos que tratamos, también es verdad que, no siempre, están al alcance de todos. Un conocimiento básico de las cosas más complicadas, es posible. También la relatividad general y la mecánica cuántica, se consideraron, cuando eran nuevas, como unas ideas demasiado difíciles para que cualquiera las entendiera, salvo los expertos –pero ambas se basan en conceptos sencillos que son inteligibles para cualquier persona lega en la materia, siempre que esté dispuesta a aceptar su parte matemática con los ojos cerrados-. E la misma manera, el Caos y la Complejidad, también pueden ser entendidos y, si tenemos la suerte de tener un buen interlocutor que nos sepa explicar, aquellos conceptos básicos sobre los que se asientan tanto el Caos como la Complejidad, veremos maravillados como, de manera natural, la luz se hace en nosotros y podemos entender lo que antes nos parecía inalcanzable.

Se cree que las galaxias se han formado por la acumulación gravitacional de gas, algún tiempo después de la época de la recombinación. Las nubes de gas podrían haber comenzado a formar estrellas, quizás como resultado de las colisiones mutuas. El tipo de galaxia generado podría depender del ritmo al que el gas era transformado en estrellas, formándose las elípticas cuando el gas se convertía rápidamente en estrellas, y las espirales si la transformación de estrellas era lo suficientemente lenta como para permitir crecer de forma significativa un disco de gas.

                  Nubes moleculares en Orión que son los materiales primigenios para complejidades futuras

Las galaxias evolucionan al convertir progresivamente su gas remanente en estrellas, si bien no existe probablemente una evolución entre las diferentes tipos de la clasificación del conocido sistema de Hubble. No obstante, algunas galaxias elípticas pudieron haberse creado por la colisión y posterior fusión de dos galaxias espirales.

NGC 5426 y NGC 5427 son dos galaxias espirales de tamaños similares involucradas en una danza espectacular. No es seguro que esta interacción culmine en una colisión y a la larga en la fusión de las dos galaxias, aunque éstas ya han sido ya afectadas. Conocidas ambas con el nombre de Arp 271, su danza perdurará por decenas de millones de años, creando nuevas estrellas como resultado de la mutua atracción gravitacional entre las galaxias, un tirón observable en el borde de las estrellas que ya conectan a ambas. Ubicada a 90 millones de años-luz de distancia hacia la constelación de Virgo (la Virgen), el par Arp 271 tiene unos 130.000 años-luz de extensión. Fue descubierta originalmente en 1785 por William Herschel. Muy posiblemente nuestra Vía Láctea sufrirá una colisión similar en unos cinco mil millones de años más con la galaxia vecina Andrómeda, que ahora está ubicada a cerca de 2,6 millones de años-luz de la Vía Láctea.

Sí, mirando las imagenes nos da la sensación de que está por llegar cierto Caos y Complejidad a la región del universo en la que se sitúan las dos galaxias.

Tenemos que entender que, algunos sistemas (“sistema” no es más que una palabra de la jerga científica para asignar cualquier cosa, como un péndulo que oscila, o el sistema solar, o el agua que gotea de un grifo) son muy sensibles a sus condiciones de partida, de tal modo que una diferencia mínima en el “impulso” inicial que les damos ocasiona una gran diferencia en cómo van a acabar, y existe una retroalimentación, de manera que lo que un sistema hace afecta a su propio comportamiento. Así, a primera vista, parece que la guía es sencilla y, nos puede parecer mentira que así sea. Sin embargo, esa es la premisa que debemos tener en cuenta. Nos podríamos preguntar: ¿Es realmente verdad, que todo este asunto del Caos y de la Complejidad se basaba en dos ideas sencillas –la sensibilidad de un sistema a sus condiciones de partida, y la retroalimentación-¿ La respuesta es que sí.

La mayor parte de los objetos que pueden verse en el cielo nocturno son estrellas, unos pocos centenares son visibles a simple vista. Una estrella es una bola caliente principalmente compuesta por hidrógeno gaseoso. El Sol es un ejemplo de una estrella típica y común. La gravedad impide que el gas se evapore en el espacio y la presión, debida a la alta temperatura de la estrella, y la densidad impiden que la bola encoja. En el corazón de la estrella, la temperatura y la densidad son lo suficientemente altas para sustentar a las reacciones de fusión nuclear, y la energía, producida por estas reacciones, hace su camino a la superficie y la irradia al espacio en forma de calor y luz. Cuando se agota el combustible de las reacciones de fusión, la estructura de la estrella cambia. El proceso de producir elementos, cada vez más pesados, a partir de los más livianos y de ajustar la estructura interna para balancear gravedad y presión, es llamado evolución estelar.

Observar una estrella a través del telescopio permite conocer muchas de sus importantes propiedades. El color de una estrella es un indicador de su temperatura y ésta, a su vez, depende de una combinación entre la masa de la estrella y su fase evolutiva. Usualmente, las observaciones también permiten encontrar la luminosidad de la estrella o la tasa con la cual ella irradia energía, en forma de calor y luz.

Todas las estrellas visibles a simple vista forman parte de nuestra galaxia, la Vía Láctea. La Vía Láctea es un sistema compuesto por unos cien mil millones de estrellas, junto con una considerable cantidad de material interestelar. La galaxia tiene forma de un disco chato sumergido en un halo débil y esférico. La gravedad impide que las estrellas se escapen y, sus movimientos, hacen que el sistema no colapse. La Vía Láctea no posee un límite definido, la distribución de las estrellas decrece gradualmente con distancias crecientes del centro. El SDSS detecta estrellas más de un millón de veces más débiles que las que podemos ver a simple vista, lo suficientemente lejos para ver la estructura de la Vía Láctea.

De algún modo, esto es como decir que “todo lo que hay” sobre la teoría especial de la relatividad es que la velocidad de la luz es la misma para todos los observadores. Sin embargo, la complejidad de la estructura que se levanta sobre este hecho sencillo resulta asombrosa y requiere algunos conocimientos matemáticos para poder apreciarla plenamente. Claro que, eso no quita para que, un buen comunicador le pueda transmitir a otras personas mediante explicaciones sencillas lo esencial de la relatividad especial y general y también, sobre la esencia de la mecánica cuántica, y, de la misma manera, podríamos hablar del Caos y de la Complejidad. Debemos ser conscientes de que, el Caos, puede surgir a partir del Orden y que, la Complejidad, siempre llega a través de la sencillez de un comienzo. Podemos estar al borde del Caos y, de manera milagrosa ver que también a partir de él surge la normalidad y lo nuevo que no en pocas ocasiones pueden ser nuevas formas de vida. De la misma manera, las transformaciones de los elementos sencillos, bajo ciertas condiciones, llegan a adquirir una complejidad inusitada que, de alguna manera, es necesaria para que en este mundo que nos rodea, existan seres que como nosotros, sean el ejemplo más real y de más alto nivel que está presente en el Universo. Y, de la misma manera que nosotros estamos aquí, en un minúsculo sistema solar habitando un pequeño planeta que reúne todas las condiciones necesarias para la vida, de la misma forma digo, estarán poblados otros muchos planetas de otros muchos sistemas solares repartidos por nuestra Galaxia y por las otras que, a cientos de miles pululan por el Universo, y, todos esos seres “racionales”, se preguntaran las mismas cosas que nosotros y estarán interesados en descubrir los mismos misterios, los mismos secretos de la Naturaleza que, presintiendo que existen, tienen la intuición de que serán las respuestas esperadas para solucionar muchos de los problemas e inseguridades que ahora, en nuestro tiempo, nos aquejan.

Claro que, la mente nunca descansa. Acordaos de Aristarco de Samos que, en el siglo III a. C., ya anunció que la Tierra orbitaba alrededor del Sol y, Copérnico, que se llevó el premio, no lo dijo hasta el año 1543. Esto nos viene a demostrar que, a pesar de la complejidad del mundo, lo realmente complejo está en nosotros, en nuestras mentes que, presienten lo que pueda ser, intuyen el por qué de las cosas, fabrican pensamientos que, mucho más rápidos que la luz, llegan a las galaxias lejanas y, con los ojos de la mente pueden, atisbar aquellas cosas de las que, en silencio, ha oído hablar a su intuición dentro de su mente siempre atenta a todo aquello que puede ser una novedad, una explicación, un descubrimiento.

Vista de la Tierra y el Sol de la órbita (la imagen de la tierra tomada de http://visibleearth.nasa.gov)

Ahora estamos centrados en el futuro aquí en la Tierra pero, sin dejar de la mano ese futuro que nos espera en el espacio exterior. Es pronto aún para que el hombre vaya a las estrellas pero, algún día, ese será su destino y, desde ya, debe ir preparándose para esa aventura que sólo está a la espera de tener los medios tecnológicos necesarios para hacerla posible. Mientras tanto, jugamos con las sondas espaciales que enviamos a planetas vecinos para que, nos vayan informando de lo que están hechos aquellos mundos –grandes y pequeños- que, en relativamente poco tiempo, serán visitados por nuestra especie para preparar el salto mayor.

emilio silvera

[?]

                                                        No todos vemos el mundo de la misma manera

Nuestra realidad es la que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”     Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.

Lo cierto es que, la única realidad vendrá de los descubrimientos que son desvelados y nos muestran los secretos d ela Naturaleza.

Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, para ello, encontramos las maneras de aproximarnos a esa realidad “presentida”.

Las matemáticas, con ayuda de los ordenadores, nos enseñan a bailar la danza celestial.

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.

Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas  y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.

             En esta aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado.

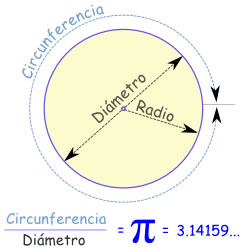
Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:

1 – 1/3 + 1/5 – 1/7 ….

Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente,  se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que  independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y  entre otros temas. Si hablamos de Pi mos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN  el Efecto mariposa y la Torah, entre otras muchísimas cosas que  se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes reopresentado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.

No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la Teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa” “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

El eterno e irracional número Pi

Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.

El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.

Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.

Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

Este famoso número como todos sabemos es irracional, lo que significa que es un número con infinitas cifras decimales que no se repiten nunca. Claro que Pi, son muchas más cosas.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.

¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.

3.1415926535897932384626433832795028841971693993…

 Muchos son los secretos matemáticos que no hemos podido desvelar

Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th

Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejmplo:

Roger Penrose dedicó bastante más tinta en defender  los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.

Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

                     ¿Es la verdad inalcanzable?

Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.

Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos  y dispares pensamientos:

• Los Computadores nunca podrán reemplazar la estupidez humana.
• El hombre nace ignorante,  la educación lo idiotiza.
• Una persona inteligente resuelve problemas, el genio los evita.
• Las mujeres consideran que guardar un secreto, es no revelar la fuente.
• Todas las mujeres tienen algo bonito… así sea una prima lejana.
• La felicidad es una lata de atún, pero con el abrelatas un poco distante.
• El único animal que no resiste aplausos es el mosquito.
• El amor está en el cerebro, no en el corazón.
• Definición de nostalgia “es la alegría de estar triste”.
• “Mi segundo órgano favorito es el cerebro”.

El día que la Inteligencia Artificial llegue a comprender por sí misma, se pueda reparar, sepa tomar decisiones en un momento dado imprevisto a un problema surgido inesperado, pueda llegar a tener ideas propias y… hasta sentimientos…. ¿Qué haremos nosotros entonces?

Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!

Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?

     Todo eso está bien pero, ¿Quien o qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene el mismo área que el circulo”.

[?]