Ago
2
Causalidad ¡Ese Principio!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (8)
Comments (8)


Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso. Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.
Parecía como si la explicación de Fitzgerald insinuara que la naturaleza conspiraba con objeto de impedir que el hombre midiera el movimiento absoluto, para lo cual introducía un efecto que anulaba cualquier diferencia aprovechable para detectar dicho movimiento.
Este asombroso fenómeno recibió el nombre de contracción de Fitzgerald, y su autor formuló una ecuación para el mismo, que referido a la contracción de un cuerpo móvil, fue predicha igualmente y de manera independiente por H. A. Lorentz (1.853 – 1.928) de manera que, finalmente, se quedaron unidos como contracción de Lorentz-Fitzgerald.


A la contracción, Einstein le dio un marco teórico en la teoría especial de la relatividad. En esta teoría, un objeto de longitud l0 en reposo en un sistema de referencia parecerá, para un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud ![]() , donde c es la velocidad de la luz. La hipótesis original atribuía esta contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.
, donde c es la velocidad de la luz. La hipótesis original atribuía esta contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.
Un objeto que se moviera a 11,2 Km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 Km/s (la mitad de la velocidad de la luz) sería del 15%; a 262.000 Km/s (7/8 de la velocidad de la luz), del 50%. Es decir, que una regla de 30 cm que pasara ante nuestra vista a 262.000 Km/s nos parecería que mide sólo 15’24 cm, siempre y cuando conociéramos alguna manera para medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 Km/s en números redondos, su longitud en la dirección del movimiento sería cero. Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse el universo.
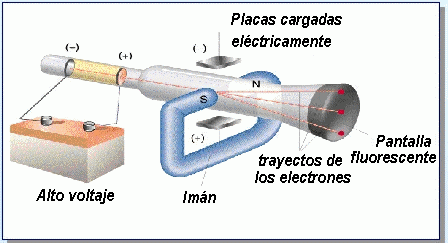
El físico holandés Henrik Antón Lorentz, como hemos dicho, promovió esta idea pensando en los rayos catódicos (que ocupaban su actividad por aquellas fechas). Se hizo el siguiente razonamiento: si se comprimiera la carga de una partícula para reducir su volumen, aumentaría su masa. Por consiguiente, una partícula voladora, escorzada en la dirección de su desplazamiento por la contracción de Fitzgerald, debería crecer en términos de masa. Lorentz presentó una ecuación sobre el acrecentamiento de la masa, que resultó muy similar a la ecuación de Fitzgerald sobre el acortamiento. A 149.637 Km/s la masa de un electrón aumentaría en un 15%; a 262.000 Km/s, en un 100% (es decir, la masa se duplicaría); y a la velocidad de la luz, su masa sería infinita. Una vez más pareció que no podría haber ninguna velocidad superior a la de la luz, pues, ¿cómo podría ser una masa mayor que infinita?

El efecto Fitzgerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas como las ecuaciones Lorentz-Fitzgerald.
Mientras que la contracción Fitzgerald no podía ser objeto de mediciones, el efecto Lorentz sobre masas sí podía serlo, aunque indirectamente. De hecho, el muón tomó 10 veces su masa original cuando fue lanzado, a velocidades relativistas, en el acelerador de partículas, lo que confirmó la ecuación de Lorentz. Los experimentos posteriores han confirmado las ecuaciones de ambos: a velocidades relativistas, las longitudes se contraen y las masas se incrementan.
Como es conocido por todos, Einstein adoptó estos descubrimientos y los incorporó a su teoría de la relatividad especial, que aunque mucho más amplia, recoge la contracción de Fitzgerald y el aumento de la masa de Lorentz cuando se alcanzan grandes velocidades.
Algunas veces pienso que los artistas en general, y los poetas en particular, tendrían que adaptar e incluir en sus esquemas artísticos y poéticos los adelantos científicos, para asimilarlos en las diversas expresiones y sentimientos que serán después puestos al servicio del consumo humano. Estos adelantos científicos serían así coloreados con las pasiones humanas, y transformados, de alguna forma, en la sangre, y por qué no, los sentimientos de la naturaleza humana. Posiblemente, de haberlo hecho, el grado general de conocimiento sería mayor. De todas las maneras, no dejamos de avanzar en el conocimiento de la Naturaleza.
Hacemos mil y un inventos para poder llegar a lugares que, hasta hace muy poco tiempo se pensaba que nos estaban vedados. Y, a pesar de ello, la cultura científica, en general es pobre. Sólo uno de cada tres puede definir una molécula o nombrar a un solo científico vivo. De veinticinco licenciados escogidos al azar en la ceremonia de graduación de Harvard, sólo dos pudieron explicar por qué hace más calor en verano que en invierno. La respuesta, dicho sea de paso, no es “porque el Sol está más cerca”; no está más cerca. El eje de rotación de la Tierra está inclinado, así que cuando el hemisferio norte se inclina hacia el Sol, los rayos son más perpendiculares a la superficie, y la mitad del globo disfruta del verano. Al otro hemisferio llegan rayos oblicuos: es invierno. Es triste ver cómo aquellos graduados de Harvard podían ser tan ignorantes. ¡Aquí los tenemos con faltas de ortografía!
Por supuesto, hay momentos brillantes en los que la gente se sorprende. Hace años, en una línea de metro de Manhattan, un hombre mayor se las veía y deseaba con un problema de cálculo elemental de su libro de texto de la escuela nocturna; no hacía más que resoplar. Se volvió desesperado hacia el extraño que tenía a su lado, sentado junto a él, y le preguntó si sabía cálculo. El extraño afirmó con la cabeza y se puso a resolverle al hombre el problema. Claro que no todos los días un anciano estudia cálculo en el metro al lado del físico teórico ganador del Nobel de Física, T. D. Lee.

Leon Lederman cuenta una anécdota parecida a la del tren, pero con final diferente. Salía de Chicago en un tren de cercanías cuando una enfermera subió a él a la cabeza de un grupo de pacientes de un hospital psiquiátrico local. Se colocaron a su alrededor y la enfermera se puso a contarlos: “uno, dos tres…”. Se quedó mirando a Lederman y preguntó “¿quién es usted?”; “soy Leon Lederman” – respondió – “ganador del premio Nobel y director del Fermilab”. Lo señaló y siguió tristemente “sí claro, cuatro, cinco, seis…”. Son cosas que ocurren a los humanos; ¡tan insignificantes y tan grandes! Somos capaces de lo mejor y de lo peor. Ahí tenemos la historia para ver los ejemplos de ello.

Pero ahora más en serio, es necesario preocuparse por la incultura científica reinante, entre otras muchas razones porque la ciencia, la técnica y el bienestar público están cada día más conectados. Y, además, es una verdadera pena perderse la concepción del mundo que, en parte, he plasmado en estas páginas. Aunque aparezca incompleta, se puede vislumbrar que posee grandiosidad y belleza, y va asomándose ya su simplicidad.
“El proceso de la ciencia es el descubrimiento a cada paso de un nuevo orden que de unidad a lo que desde hacía tiempo parecía desunirlo.”
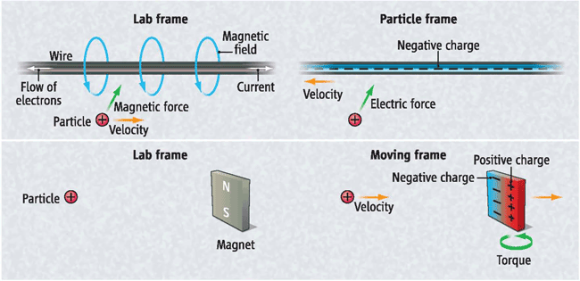
– Es lo que hizo Faraday cuando cerró el vínculo que unió la electricidad y el magnetismo.
– Es lo que hizo Clerk Maxwell cuando unió aquélla y éste con la luz.
– Einstein unió el tiempo y el espacio, la masa a la energía y relacionó las grandes masas cosmológicas con la curvatura y la distorsión del tiempo y el espacio para traernos la gravedad en un teoría moderna; y dedicó los últimos años de su vida al intento de añadir a estas similitudes otra manera nueva y más avanzada, que instaurara un orden nuevo e imaginativo entre las ecuaciones de Maxwell y su propia geometría de la gravitación.
Algunos momentos de la vida del Maestro
Cuando Coleridge intentaba definir la belleza, volvía siempre a un pensamiento profundo: la belleza, decía, “es la unidad de la variedad”. La ciencia no es otra cosa que la empresa de descubrir la unidad en la variedad desaforada de la naturaleza, o más exactamente, en la variedad de nuestra experiencia que está limitada por nuestra ignorancia.”
Hay muchas cosas que no podemos controlar, sin embargo, algo dentro de nosotros, nos envía mensajes sobre lo que podría ser importante para que nos fijemos mejor y continuemos profundizando.
Para comprender mejor el panorama, hagamos una excursión hasta la astrofísica; hay que explicar por qué la física de partículas y la astrofísica se han fundido no hace muchos años, en un nivel nuevo de intimidad, al que alguien llamó la conexión espacio interior/espacio exterior.
Mientras los expertos del espacio interior construían aceleradores, microscopios cada vez más potentes para ver qué pasaba en el dominio subnuclear, los colegas del espacio exterior sintetizaban los datos que tomaban unos telescopios cada vez más potentes, equipados con nuevas técnicas cuyo objeto era aumentar su sensibilidad y la capacidad de ver detalles finos. Otro gran avance fueron los observatorios establecidos en el espacio, con sus instrumentos para detectar infrarrojos, ultravioletas, rayos X y rayos gamma; en pocas palabras, toda la extensión del espectro electromagnético, muy buena parte del cual era bloqueado por nuestra atmósfera opaca y distorsionadora.
¿Hasta donde llegaremos?
La síntesis de la cosmología de los últimos cien años es el modelo cosmológico estándar. Sostiene que el universo empezó en forma de un estado caliente, denso, compacto, hace unos 15.000 millones de años. El universo era entonces infinitamente, o casi infinitamente, denso; infinita, o casi infinitamente, caliente. La descripción “infinito” es incómoda para los físicos; los modificadores son el resultado de la influencia difuminadota de la teoría cuántica. Por razones que quizá no conozcamos nunca, el universo estalló, y desde entonces ha estado expandiéndose y enfriándose.
Ahora bien, ¿cómo se han enterado de eso los cosmólogos? El modelo de la Gran Explosión (Big Bang) nació en los años treinta tras el descubrimiento de que las galaxias (conjuntos de 100.000 millones de estrellas, aproximadamente) se estaban separando entre sí, descubrimiento hecho por Edwin Hubble, que andaba midiendo sus velocidades en 1.929.
Hubble tenía que recoger de las galaxias lejanas una cantidad de luz que le permitiera resolver las líneas espectrales y compararlas con las líneas de los mismos elementos de la Tierra. Cayó en la cuenta de que todas las líneas se desplazaban sistemáticamente hacia el rojo. Se sabía que una fuente de luz que se aparta de un observador hace justo eso. El desplazamiento hacia el rojo era, de hecho, una medida de la velocidad relativa de la fuente y del observador.
Más tarde, Hubble halló que las galaxias se alejaban de él en todas las direcciones; esto era una manifestación de la expansión del espacio. Como el espacio expande las distancias entre todas las galaxias, la astrónoma Hedwina Knubble, que observase desde el planeta Penunbrio en Andrómeda, vería el mismo efecto o fenómeno: las galaxias se apartaría de ella.
Cuanto más distante sea el objeto, más deprisa se mueve. Esta es la esencia de la ley de Hubble. Su consecuencia es que, si se proyecta la película hacia atrás, las galaxias más lejanas, que se mueven más deprisa, se acercarán a los objetos más próximos, y todo el lío acabará juntándose y se acumulará en un volumen muy, muy pequeño, como, según se calcula actualmente, ocurría hace 15.000 millones de años.
La más famosa de las metáforas científicas te pide que imagines que eres una criatura bidimensional, un habitante del Plano. Conoces el este y el oeste, el norte y el sur, pero arriba y abajo no existen; sacaos el arriba y debajo de vuestras mentes. Vivís en la superficie de un globo que se expande. Por toda la superficie hay residencias de observadores, planetas y estrellas que se acumulan en galaxias por toda la esfera; todo bidimensional. Desde cualquier atalaya, todos los objetos se apartan a medida que la superficie se expande sin cesar. La distancia entre dos puntos cualesquiera de este universo crece. Eso es lo que pasa, precisamente, en nuestro mundo tridimensional. La otra virtud de esta metáfora es que, en nuestro universo, no hay ningún lugar especial. Todos los sitios o puntos de la superficie sin democráticamente iguales a todos los demás. No hay centro; no hay borde. No hay peligro de caerse del universo. Como nuestra metáfora del universo en expansión (la superficie del globo) es lo único que conocemos, no es que las estrellas se precipiten dentro del espacio. Lo que se expande es que espacio que lleva toda la barahúnda. No es fácil visualizar una expansión que ocurre en todo el universo. No hay un exterior, no hay un interior. Sólo hay este universo que se expande. ¿En qué se expande? Pensad otra vez en vuestra vida como habitante del Plano, de la superficie del globo: en nuestra metáfora no existe nada más que la superficie.


Instalaciones en las entrañas de la Tierra que posibilitan viajar a lo más profundo de la materia
Hemos inventado tecnología que ha posibilitado que no estemos confinados en el planeta
“Cuánto más profundizo en el conocimiento de las cosas más consciente soy de lo poco que se. Mientras que mis conocimientos son finitos, mi ignorancia es ilimitada.”
Dos consecuencias adicionales de gran importancia que tiene la teoría del Big Bang acabaron por acallar la oposición, y ahora reina un considerable consenso. Una es la predicción de que la luz de la incandescencia original (presuponiendo que fue muy caliente) todavía está a nuestro alrededor, en forma de radiación remanente. Recordad que la luz está constituida por fotones, y que la energía de los fotones está en relación inversa con la longitud de onda. Una consecuencia de la expansión del universo es que todas las longitudes se expanden. Se predijo, pues, que las longitudes de onda, originalmente infinitesimales, como correspondía a unos fotones de gran energía, han crecido hasta pertenecer ahora a la región de las microondas, en la que las longitudes son unos pocos milímetros.
En 1.965 se descubrieron los rescoldos del Big Bang, es decir, la radiación de fondo de microondas. Esos fotones bañan el universo entero, y se mueven en todas las direcciones posibles. Los fotones que emprendieron viaje hace miles de millones de años cuando el universo era más pequeño y caliente, fueron descubiertos por una antena de los laboratorios Bell en Nueva Jersey.
Así que el descubrimiento hizo imprescindible medir la distribución de las longitudes de onda, y se hizo. Por medio de la ecuación de Planck, esta medición de la temperatura media de lo que quiera (el espacio, las estrellas, polvo, un satélite, los pitidos de un satélite que se hubiese colado ocasionalmente) que haya estado bañándose en esos fotones.
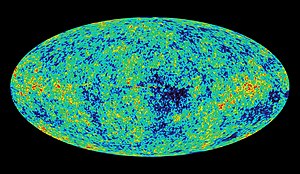
Las mediciones últimas efectuadas por la NASA con el satélite COBE dieron un resultado de 2’73 grados sobre el cero absoluto (2’73 ºK). Esta radiación remanente es una prueba muy potente a favor de la teoría del Big Bang caliente.
Los astrofísicos pueden hablar tan categóricamente porque han calculado qué distancias separaban a dos regiones del cielo en el momento en que se emitió la radiación de microondas observadas por el COBE. Ese momento ocurrió 300.000 años después del Big Bang, no tan pronto como sería deseable, pero sí lo más cerca del principio que podemos.
Resulta que temperaturas iguales en regiones separadas del espacio que nunca habían estado en contacto y cuyas separaciones eran tan grandes que ni siquiera a la velocidad de la luz daba tiempo para que las dos regiones se comunicasen, y sin embargo, sí tenían la misma temperatura. La teoría del Big Bang no podía explicarlo; ¿un fallo?, ¿un milagro? Se dio en llamar a eso la crisis de la causalidad, o de la isotropía.

Considerado a grandes escalas, el Universo es isotrópico
De la causalidad porque parecía que había una conexión causal entre distintas regiones del cielo que nunca debieran haber estado en contacto; de la isotropía porque donde quiera que mires a gran escala verás prácticamente el mismo patrón de estrellas, galaxias, cúmulos y polvo estelar. Se podría sobrellevar esto en un modelo del Big Bang diciendo que la similitud de las miles de millones de piezas del universo que nunca estuvieron en contacto es puro accidente. Pero no nos gustan los “accidentes”: los milagros están estupendamente si jugamos a la lotería, pero no en la ciencia. Cuando se ve uno, los científicos sospechan que algo más importante se nos mueve entre bastidores. Me parece que mi inclinación científica me hace poco receptivo a los milagros. Si algo para habrá que buscar la causa.

El segundo éxito de gran importancia del modelo del Big Bang tiene que ver con la composición de nuestro universo. Puede parecer que el mundo está hecho de aire, tierra, agua y fuego, pero si echamos un vistazo arriba y medimos con nuestros telescopios espectroscópicos, apenas sí encontramos algo más que hidrógeno, y luego helio. Entre ambos suman el 98% del universo que podemos ver. El resto se compone de los otros noventa elementos. Sabemos gracias a nuestros telescopios espectroscópicos las cantidades relativas de los elementos ligero, y hete aquí que los teóricos del Big Bang dicen que esas abundancias son precisamente las que cabría esperar. Lo sabemos así.
El universo prenatal tenía en sí toda la materia del universo que hoy observamos, es decir, unos cien mil millones de galaxias, cada una con cien mil millones de soles. Todo lo que hoy podemos ver estaba comprimido en un volumen muchísimos menos que la cabeza de un alfiler. La temperatura era alta, unos 1032 grados Kelvin, mucho más caliente que nuestros 273 ºK actuales. Y en consecuencia la materia estaba descompuesta en sus componentes primordiales.
Una imagen aceptable de aquello es la de una “sopa caliente”, o plasma, de quarks y leptones (o lo que haya dentro, si es que hay algo) en la que chocan unos contra otros con energías del orden de 1018 GeV, o un billón de veces la energía del mayor colisionador que cualquier físico pueda imaginarse construir. La gravedad era rugiente, con su poderoso (pero aún mal conocido) influjo en esta escala microscópica.
Tras este comienzo fantástico, vinieron la expansión y el enfriamiento. A medida que el universo se enfriaba, las colisiones eran menos violentas. Los quarks, en contacto íntimo los unos con los otros como partes del denso grumo que era el universo infantil, empezaron a coagularse en protones, neutrones y los demás hadrones. Antes, esas uniones se habrían descompuesto en las inmediatas y violentas colisiones, pero el enfriamiento no cesaba; aumentaba con la expansión y las colisiones eran cada vez más suaves.

La máquina del big bang reveló que, en aquellos primeros momentos…
Aparecieron los protones y los neutrones, y se formaran núcleos estables. Este fue el periodo de nucleosíntesis, y como se sabe lo suficiente de física nuclear se pueden calcular las abundancias relativas de los elementos químicos que se formaron. Son los núcleos de elementos muy ligeros; los más pesados requieren de una “cocción” lenta en las estrellas.
Claro que, los átomos (núcleos más electrones) no se formaron hasta que la temperatura no cayó lo suficiente como para que los electrones se organizaran alrededor de los núcleos, lo que ocurrió 300.000 años después, más o menos. Así que, en cuanto se formaron los átomos neutros, los fotones pudieron moverse libremente, y ésta es la razón de que tengamos una información de fotones de microondas todavía.
La nucleosíntesis fue un éxito: las abundancias calculadas y las medidas coincidían. Como los cálculos son una mezcla íntima de física nuclear, reacciones de interacción débil y condiciones del universo primitivo, esa coincidencia es un apoyo muy fuerte para la teoría del Big Bang.

En realidad, el universo primitivo no era más que un laboratorio de acelerador con un presupuesto ilimitado. Nuestros astrofísicos tenían que saberlo todo acerca de los quarks y los leptones y las fuerzas para construir un modelo de evolución del universo. Los físicos de partículas reciben datos de su experimento grande y único. Por supuesto, para los tiempos anteriores a los 10-13 segundos, están mucho menos seguros de las leyes de la física. Así que, los astrofísicos azuzan a los teóricos de partículas para que se remanguen y contribuyan al torrente de artículos que los físicos teóricos lanzan al mundo con sus ideas: Higgs, unificación de cuerdas vibrantes, compuestos (qué hay dentro de los quarks) y un enjambre de teorías especulativas que se aventuran más allá del modelo estándar para construir un puente que nos lleve a la descripción perfecta del universo, de la Naturaleza. ¿Será posible algún día?
Esperemos a ver qué pasa con la historia que comenzaron Grabielle Veneziano, John Schwartz, André Neveu, Pierre Ramond, Jeff Harvey, Joel Sheik, Michael Green, David Gross y un dotado flautista de Hamelin que responde al nombre de Edward Witten.
La teoría de cuerdas es una teoría que nos habla de un lugar muy distante. Dice Leon Lederman que casi tan distante como Oz o la Atlántida; hablamos del dominio de Planck. No ha forma de que podamos imaginar datos experimentales en ese tiempo tan lejano; las energías necesarias (las de la masa de Planck) no están a nuestro alcance, lo que significa que no debemos perseverar.

Por lejos que esté… Siempre querremos llegar. ¿Qué habrá allí dónde nuestra vista no llega? ¿Cómo será aquel universo?
¿Por qué no podemos encontrar una teoría matemáticamente coherente (sin infinitos) que describa de alguna manera Oz? ¡Dejar de soñar, como de reír, no es bueno!
Pero en verdad, al final de todo esto, el problema es que siempre estarmos haciendo preguntas: Que si la masa crítica, que si el universo abierto, plano o cerrado… Que si la materia y energía del universo es más de la que se ve. Pasa lo contrario que con nuestra sabiduría (queremos hacer ver que hay más… ¡de la que hay!), que parece mucha y en realidad es tan poca que ni podemos contestar preguntas sencillas como, por ejemplo: ¿Quiénes somos?

Ahí, ante esa pregunta “sencilla” nos sale una imagen movida que no deja ver con claridad
Sin embargo, hemos sabido imaginar para poder desvelar algunos otros secretos del universo, de la Naturaleza, del Mundo que nos acoge y, sabemos cómo nacen, viven y mueren las estrellas y lo que es una galaxia. Podemos dar cuenta de muchas cuestiones científicas mediante modelos que hemos ideado para explicar las cosas. No podemos físicamente llegar a otras galaxias y nos hemos inventado telescopios de inmensa capacidad para llegar hasta las galaxias situadas a 12.000 millones de años luz de la Tierra. También, hemos sabido descifrar el ADN y, si ninguna catástrofe lo remedia… ¡Viajaremos por las estrellas!
Claro que, sabemos representar los Modelos de Universo que imaginamos, y, aún no hemos llegado a saber lo que el Universo es. ¡Nuestra imaginación! que siempre irá por delante de la realidad que nos rodea y que no siempre sabemos ver. Todo es, como dijo aquel, la belleza que se nos regala: “La unidad de la variedad”. Además, no debemos olvidar que, todo lo grande está hecho de cosas pequeñas.
emilio silvera
















 Totales: 75.635.080
Totales: 75.635.080 Conectados: 66
Conectados: 66




































el 2 de agosto del 2016 a las 19:03
¿Qué significa que una masa tiende a infinito cuando se acerca a la velocidad de la luz?
¿Es posible que una masa que se “aplasta” pueda hacerse infinita? No se rompería mucho antes antes que eso ocurriera?
O solo es un efecto relativo.
¿Por qué no decir que se desintegrará en una infinidad de elementos?
Qué opinais compañeros.
el 3 de agosto del 2016 a las 0:02
el 3 de agosto del 2016 a las 0:08
Bueno… mis disculpas por la forma del comentario. Espero se pueda leer bien.
el 3 de agosto del 2016 a las 10:31
Comentario a Nelson:
Improviso la parrafada siguiente en mi confianza de que pueda ser aclaratoria
F = dp/dt = d(mv)/dt =m a es la definición de fuerza
Si se supusiera otra relación a lo mejor estuviéramos ante una fuerza especial
F’ = v/m v=F’/m, a mayor masa v sería menor y F’= m v constante (“Fuerza constante de inercia”)
Una masa no podría alcanzar la velocidad de la luz. Eso sería en nuestra dimensión de materia normal, donde el fotón posee la masa mínima (O cero según unos o la más pequeña que se da para la materia normal según otros)
Lo cierto es que la velocidad en el vacío depende del medio “vacío” que de vacío nada.
La lógica del movimiento implica que “la barrera material” que supone navegar por el vacío es mayor cuanto mayor sea la masa (Su número de componentes elementales y su “tamaño”)
Claro que para que la masa se haga tan grande, o mejor dicho, tan extensa en el sentido perpendicular de marcha (La contracción de Lorenz según la dirección de la velocidad), la energía aplicada para que eso ocurra ha de ser muy grande, pues la estructura normal de una partícula por ejemplo, no será la de esa fina extensión. La estructura se estiraría tanto que terminaría por romperse en pedazos (Dejaría de ser lo que era y se fragmentaria como ocurre con la estructura entre quarks, para formarse otros de nuevo a partir de los fragmentos). Para que eso ocurra no será necesario que se llegue al extremo de alcanzar la velocidad de la luz, en que matemáticamente la masa se haría infinita, con la infinita energía que eso requiere.
En ese orden de cosas, este forzado de velocidades pudiera ser el origen de la multiplicación de las partículas.
Un cierto aumento en la densidad de vacío para que procure una expansión acelerada, requería que los elementos se multiplicasen constantemente. ¿Sería posible que esto fuera una consecuencia de la variabilidad de velocidad debida a los taquiones o es algo más profundo, la resolución de los elementos como pequeños universos de densidad infinita?
Aunque en otro orden, en cierto modo es lo que se procura en los aceleradores de partículas, cuando chocan entre ellas, aunque no se haga contra el “vacío”(¿?), lo que vendría a ser una cuestión de escala y de energía puesta en juego.
La velocidad de la luz un absoluto, no es de recibo, salvo que nos estemos refiriendo a la materia normal. Hay tantas demostraciones de que no es así, que yo diré solo una: el taquión es posible y como mínimo debió darse con el Big-Bang cuando ni siquiera la luz (Fotón normalizado) habría existido. No se puede aceptar que la velocidad de la luz sea un absoluto. Los absolutos no pueden existir, bajo el Todo, todo es relativo. Realmente la velocidad de luz como la máxima no deja de ser un postulado.
Ni siquiera el espacio tiempo como una densidad absoluta podría darse.
La masa propia y la masa relativa-inercial no pueden sumarse así como así, sino que su acumulación se da de otra manera. La masa inercial solo afectará a la masa propia o mejor dicho a la partícula o elemento de que se trate, en una dirección, la de su velocidad. Lo que supondría que se afectara en gran aproximación solo en su mitad.
Suponiendo unos efectos de fuerzas globales sobre la masa, equilibradas y transversales en la forma que sea sobre la partícula, serán diferentes de los causados a la masa en la dirección de su velocidad.
No sé si el efecto de no suma simple se corrige con Lorenz realmente.
Lo de que la masa relativista no es constante, no se ve a simple vista. Para acelerar una partícula o masa la fuerza no ha de permanecer sobre ella todo el tiempo, sino que es suficiente con el impulso inicial. Ella continuará con la velocidad obtenida. Es por causa de la propia inercia, o rozamiento con el “vacío” cuando la velocidad irá decayendo, pero muy lentamente. Esta bajada de velocidad será más pronunciada si excede con mucho de su velocidad propia. Es por eso que acelerarla cada vez más requiere de tanta energía.
La masa puede permanecer muy aproximadamente con la velocidad adquirida, y de tratarse de la velocidad propia permanecerá constante.
F = dp/dt = (dm/dt).v + m.(dv/dt) = (dm/dt).v + ma (Lorentz)
Este resultado requeriría un estudio sobre la relación entre inercia y partícula. Por qué las velocidades internas y rotaciones permanecen globalmente constantes (Una relación interior que procure las propias masas propias componentes para el total de la partícula), y cómo es la relación de estas constantes internas con la velocidad externa propia de las partículas en libertad. La onda partícula De Broglie constituye una buena herramienta, cuando se saben radios, órbitas, y frecuencias de las subpartículas
Saludos compañeros
el 5 de agosto del 2016 a las 2:32
Hola muchachada.
Hola Fandila.
Gracias por el esfuerzo y la gentileza de contestarme pero como te dije no alcanzo el nivel, sobre todo cuando entran a tallar las fórmulas. En el caso del post que cité me resultó redondito el razonamiento y la conclusión, aún sin distinguir si eran correctos. Por ello te lo trasmití en la certeza de que tú podrías analizarlo.
Como no puedo ser riguroso, intento imaginar soluciones que me resulten sencillas y convincentes, aunque luego alguien calificado las destruya sin piedad. Al menos daré otro pasito para entender…
Saludos cordiales desde Montevideo.
el 4 de agosto del 2016 a las 7:58
Me encanta cuando veo a los contertulios disfrutar con el tema que tratamos y sacar sus propias conclusiones en sunsión de los antecedentes y conocimientos adquiridos. El tema es candente y, no podemos olvidar que, en los Aceleradores de partíoculas, lanzados haces de muones a velocidades cercanas a c, llegarón a incrementar su masa diez veces, dándo así la razón a la teoría de Einstein.
Seguir disfrutando que la vida es corta.
el 4 de agosto del 2016 a las 11:07
Pero claro es que la masa va en relación al efecto frenado, y el efecto frenado depende del tamaño de la partícula o lo que es lo mismo, en este caso, a la superficie que presenta al vacío, debido a la contracción en la dirección de la velocidad. En apariencia como cuando una bola barro se estrella contra una pared, solo que la pared del “vacío” no es sólida.
Pues yo, particularmente, me voy pitando a donde los amigos que más me vale la pena. Que ya me paso de la hora.
el 5 de agosto del 2016 a las 6:06
Sobre el tema, podemos hablar y hablar, argumentar y argumentar pero, en cualquier sitio que podamos mirar, más o menos, se leeran las mismas explicaciones:
Todo lo que ocurre está determinado por lo que antes pasó, esa es, amigos míos, la Causalidad.