Constantes de la Naturaleza

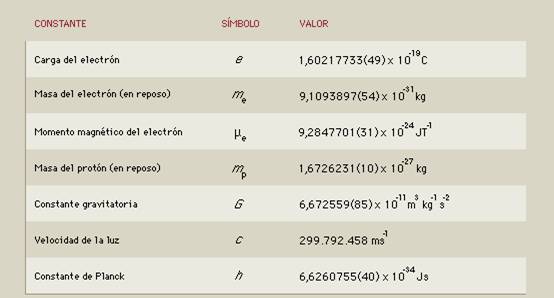
Si alguna de estas constantes de la Naturaleza, variaran tan sólo una millonésima, la vida no estaría presente

“En la Física existen una serie de magnitudes que contienen información que es independiente del sistema de medida que elijamos, lo cual es muy valioso no sólo en los cálculos. Además, estos parámetros que fija la naturaleza aparecen en las ecuaciones como parámetros que debemos ajustar lo más que podamos para que nuestras predicciones y nuestros modelos se ajusten a la realidad en la medida de lo posible.

Y aquí es donde viene el problema. Que son parámetros, es decir, su valor cuantitativo no es deducible de la teoría y por tanto hay que medirlo. Y esto añade la dificultad no sólo de idear un experimento, sino de hacerlo lo bastante preciso como para que el modelo sirva para algo.

El Modelo Estándar por ejemplo, que es el paradigma actual en el que se mueve la física de partículas y que recoge las interacciones fundamentales tiene unos 25 parámetros que se deben ajustar. Parámetros tales como la carga eléctrica, la masa, el espín, las constantes de acoplamiento de los campos, que miden la intensidad que éstos tienen, etcétera.

Ya no sólo se trata de averiguar el valor de cada una de ellas. Tampoco sabemos decir de antemano cuantas constantes fundamentales puede haber. Y es evidente que cuantas más constantes hay, más complicado se nos hace nuestro modelo.”

Si miramos hacia atrás en el Tiempo podemos contemplar los avances que la Humanidad logró en los últimos tiempos, caigo en la cuenta de que poco a poco hemos sido capaces de identificar una colección de números mágicos y misteriosos arraigados en la regularidad de la experiencia.

¡Las constantes de la naturaleza!

Dan al universo su carácter distintivo y lo hace singular, distinto a otros que podría nuestra imaginación inventar. Estos números misteriosos, a la vez que dejan al descubierto nuestros conocimientos, también dejan al desnudo nuestra enorme ignorancia sobre el universo que nos acoge. Las medimos con una precisión cada vez mayor y modelamos nuestros patrones fundamentales de masa y tiempo alrededor de su invarianza; no podemos explicar sus valores.

Nunca nadie ha explicado el valor numérico de ninguna de las constantes de la naturaleza. ¿Recordáis el 137? Ese número puro, adimensional, que guarda los secretos del electrón (e), de la luz (c) y del cuanto de acción (h). Hemos descubierto otros nuevos, hemos relacionado los viejos y hemos entendido su papel crucial para hacer que las cosas sean como son, pero la razón de sus valores sigue siendo un secreto profundamente escondido.

Buscar esos secretos ocultos implica que necesitamos desentrañar la teoría más profunda de todas y la más fundamental de las leyes de la naturaleza: descubrir si las constantes de la naturaleza que las definen están determinadas y conformadas por alguna consistencia lógica superior o si, por el contrario, sigue existiendo un papel para el azar.

Si estudiamos atentamente las constantes de la naturaleza nos encontramos con una situación muy peculiar. Mientras parece que ciertas constantes estuvieran fijadas, otras tienen espacio para ser distintas de las que son, y algunas no parecen afectadas por ninguna otra cosa del ­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­­- o en el – universo.

¿Llegaron estos valores al azar?

¿Podrían ser realmente distintos?

¿Cuán diferentes podrían ser para seguir albergando la existencia de seres vivos en el universo?

En 1.986, el libro The Anthropic Cosmological Principle exploraba las diez maneras conocidas en que la vida en el universo era sensible a los valores de las constantes universales. Universos con constantes ligeramente alteradas nacerían muertos, privados del potencial para desarrollar y sostener la complejidad que llamamos vida.

En la literatura científica puede encontrarse todo tipo de coincidencias numéricas que involucran a los valores de las constantes de la naturaleza. He aquí algunas de las fórmulas propuestas (ninguna tomada en serio) para la constante  de estructura fina.

Valor experimental: 1/α = 137’035989561…

• Lewis y Adams: 1/α = 8π (8π⁵ / 15)^1/3 = 137’384
• Eddington: 1/α = (16² – 16) / 2 + 16 – 1 = 137
• Wiler: 1/α = (8π⁴ / 9)(2⁴5! / π⁵)^1/4 = 137’036082
• Aspden y Eagles: 1/α = 108π (8 / 1.843)^1/6 = 137’035915

Por supuesto, si la teoría M da al fin con una determinación del valor de 1/α podría parecerse perfectamente a una de estas fórmulas especulativas. Sin embargo ofrecería un amplio y constante edificio teórico del que seguiría la predicción.

También tendría que haber, o mejor, que hacer, algunas predicciones de cosas que todavía no hemos medido; por ejemplo, las siguientes cifras decimales de 1/α, que los futuros experimentadores podrían buscar y comprobar con medios más adelantados que los que ahora tenemos, a todas luces insuficientes en tecnología y potencia.

Todos estos ejercicios de juegos mentales numéricos se acercan de manera impresionante al valor obtenido experimentalmente, pero el premio para el ingeniero persistente le corresponde a Gary Adamson, cuya muestra de 137-logía se mostraron en numerosas publicaciones.

Estos ejemplos tienen al menos la virtud de surgir de algún intento de formular una teoría de electromagnetismo y partículas. Pero hay también matemáticos “puros” que buscan cualquier combinación de potencias de números pequeños y constantes matemáticas importantes, como π, que se aproxime al requerido 137’035989561… He aquí algún ejemplo de este tipo.

• Robertson: 1/α = 2^-19/4 3^10/3 5^17/4 π^-2 = 137’03594
• Burger: 1/α = (137² + π²)^1/2 = 137’0360157

Unidades naturales que no inventó el hombre

Ni siquiera el gran físico teórico Werner Heisenberg pudo resistirse a la ironía o irónica sospecha de que…

“En cuanto al valor numérico, supongo que 1/α = 2⁴ 3³ / π, pero por supuesto es una broma.”

Arthur Eddington, uno de los más grandes astrofísicos del siglo XX y una notable combinación de lo profundo y lo fantástico, más que cualquier figura moderna, fue el responsable impulsor de poner en marcha los inacabables intentos de explicar las constantes de la naturaleza mediante auténticas proezas de numerología pura. Él también advirtió un aspecto nuevo y especular de las constantes de la naturaleza.

“He tenido una visión muy extraña, he tenido un sueño; supera el ingenio del hombre para decir qué sueño era. El hombre no es más que un asno cuando tiene que exponer este sueño. Se llamará el sueño del fondo, porque no tiene fondo.”

A. S. Eddington

 

“El conservadurismo recela del pensamiento, porque el pensamiento en general lleva a conclusiones erróneas, a menos que uno piense muy, muy intensamente.”

Roger Scruton

 

           Todo lo que existe… ¡Tiene una explicación!

 

Hay que prestar atención a las coincidencias. Uno de los aspectos más sorprendentes en el estudio del universo astronómico durante el siglo XX, ha sido el papel desempeñado por la coincidencia: que existiera, que fuera despreciada y que fuera recogida. Cuando los físicos empezaron a apreciar el papel de las constantes en el dominio cuántico y a explorar y explorar la nueva teoría de la gravedad de Einstein para describir el universo en conjunto, las circunstancias eran las adecuadas para que alguien tratara de unirlas.

Entró en escena Arthur Eddington; un extraordinario científico que había sido el primero en descubrir cómo se alimentaban las estrellas a partir de reacciones nucleares. También hizo importantes contribuciones a nuestra comprensión de la galaxia, escribió la primera exposición sistemática de la teoría de la relatividad general de Einstein y fue el responsable de verificar, en una prueba decisiva durante un eclipse de Sol, la veracidad de la teoría de Einstein en cuanto a que el campo gravitatorio del Sol debería desviar la luz estelar que venía hacia la Tierra en aproximadamente 1’75 segmentos de arco cuando pasaba cerca de la superficie solar, y así resultó.

Albert Einstein y Arthur Stanley Eddington se conocieron y se hicieron amigos. Se conservan fotos de los dos juntos conversando sentados en un banco en el jardín de Eddington en el año 1.930, donde fueron fotografiados por la hermana del dueño de la casa.

Aunque Eddington era un hombre tímido con pocas dotes para hablar en público, sabía escribir de forma muy bella, y sus metáforas y analogías aún las utilizan los astrónomos que buscan explicaciones gráficas a ideas complicadas. Nunca se casó y vivió en el observatorio de Cambridge, donde su hermana cuidaba de él y de su anciana madre.

Eddington creía que a partir del pensamiento puro sería posible deducir leyes y constantes de la naturaleza y predecir la existencia en el universo de cosas como estrellas y galaxias. ¡Se está saliendo con la suya!

Entre los números de Eddington, uno lo consideró importante y lo denominó “número de Eddington”, que es igual al número de protones del universo visible. Eddington calculó (a mano) este número enorme y de enorme precisión en un crucero trasatlántico concluyendo con esta memorable afirmación.

“Creo que en el universo hay

15.747.724.136.275.002.577.605.653.961.181.555.468.044.717.914.527.116.709.366.231.425.076.185.631.031.296

protones y el mismo número de electrones.”

 

Este número enorme, normalmente escrito N_Edd, es aproximadamente igual a 10⁸⁰. Lo que atrajo la atención de Eddington hacia él era el hecho de que debe ser un número entero, y por eso en principio puede ser calculado exactamente.

Durante la década de 1.920, cuando Eddington empezó su búsqueda para explicar las constantes de la naturaleza, no se conocían bien las fuerzas débil y fuerte, y las únicas constantes dimensionales de la física que sí se conocían e interpretaban con confianza eran las que definían la gravedad y las fuerzas electromagnéticas.

No siempre sabemos valorar la grandeza a la que puede llegar la mente humana: “… puedan haber accedido a ese mundo mágico de la Naturaleza para saber ver primero y desentrañar después, esos números puros y adimensionales …”

Eddington las dispuso en tres grupos o tres puros números adimensionales. Utilizando los valores experimentales de la época, tomó la razón entre las masas del protón y del electrón:

m_p / m_e ≈ 1.840

La inversa de la constante de estructura fina:

2πhc / e² ≈ 137

Y la razón entre la fuerza gravitatoria y la fuerza electromagnética entre un electrón y un protón:

e² / Gm_pm_e ≈ 10⁴⁰

A éstas unió o añadió su número cosmológico, N_Edd ≈ 10⁸⁰.

¿No cabría la posibilidad de que todos los grandes sucesos presentes correspondan a propiedades de este Gran Número [10⁴⁰] y, generalizando aún más, que la historia entera del universo corresponda a propiedades de la serie entera de los números naturales…? Hay así una posibilidad de que el viejo sueño de los filósofos de conectar la naturaleza con las propiedades de los números enteros se realice algún día.

Eddington a  estos cuatro números los llamó “las constantes últimas”, y la explicación de sus valores era el mayor desafío de la ciencia teórica.

“¿Son estas cuatro constantes irreducibles, o una unificación posterior de la física demostrará que alguna o todas ellas pueden ser prescindibles?

¿Podrían haber sido diferentes de los que realmente son?”

 

 

El Modelo estándar es la teoría que tenemos pero…

 

De momento, con certeza nadie ha podido contestar a estas dos preguntas que, como tantas otras, están a la espera de esa Gran Teoría Unificada del Todo, que por fin nos brinde las respuestas tan esperadas y buscadas por todos los grandes físicos del mundo. ¡Es todo tan complejo! ¿Acaso es sencillo y no sabemos verlo? Seguramente un poco de ambas cosas; no será tan complejo, pero nuestras mentes aún no están preparadas para ver su simple belleza. Una cosa es segura, la verdad está ahí, esperándonos.

Para poder ver con claridad no necesitamos gafas, sino evolución. Hace falta alguien que, como Einstein hace 100 años, venga con nuevas ideas y revolucione el mundo de la física que, a comienzos del siglo XXI, está necesitada de un nuevo y gran impulso. ¿Quién será el elegido? Por mi parte me da igual quién pueda ser, pero que venga pronto. Quiero ser testigo de los grandes acontecimientos que se avecinan, la teoría de supercuerdas y mucho más.

emilio silvera

[?]