https://www.youtube.com/watch?v=uPOnsGTkaQU

Hoy día podemos considerar que existen dos posturas enfrentadas acerca del funcionamiento del Universo. Por un lado están los que piensan que el Universo es cómo es debido al azar y, en el bando opuesto, están los que consideran que existe un patrón oculto, una especie de imperativo cósmico que subyace encriptado en las leyes que rigen la naturaleza, la materia, los ciclos de los planetas o la vida en general.

Ambas posturas presentan sólidos argumentos a su favor, argumentos que aunque puedan ser criticados no por ello están exentos de razón. Los que dan crédito a la posibilidad del azar básicamente sustentan su opinión en el comportamiento que observamos en las partículas a nivel fundamental. En este nivel, que es el nivel al que se encuentran las partículas más pequeñas que podemos detectar, ciertamente todo parece regirse en base a la probabilidad. Los que opinan, por el contrario, que existe una especie de “orden implicado” básicamente basan sus creencias en la irrazonable efectividad que presentan las matemáticas para describir la realidad.

La analogía del relojero es un argumento teleológico que sostiene que el diseño implica un diseñador. Ha tenido un papel prominente en la teología natural y el “argumento del diseño”, donde se ha usado para argüir a favor de la existencia de Dios y el diseño inteligente del universo.(la imagen y el pequeño texto de abajo no pertenecen al trabajo original, y, sólo se añade para hacer más dinámica la lectura).

Ciertamente parece complicado conciliar ambas posturas. Si es cierto que existe una especie de “diseño inteligente” ¿Cómo podría éste basarse en el azar o la probabilidad? Pero si, por el contrario, todo se debiera al azar ¿Cómo explicamos que nuestras leyes universales se basen en criterios que involucran una lógica racional?

La única posibilidad de unificar ambos criterios sería aceptar que existe una manera de organizar el azar de forma racional, una especie de “principio cosmo-caótico” al que hizo referencia Celeb Scharf. Si esto fuera cierto simplemente implicaría que la lógica que subyace en el comportamiento de todo cuanto acontece en el Universo sería la más simple que cabría imaginar, dado que exigiría únicamente la combinación de dos elementos: uno y su opuesto, que es la única condición que permite o acepta el criterio del azar. En otras palabras, si pudiéramos unificar ambas posturas en una teoría global o unificada implicaría que lo imposible es la única posibilidad. Pues bien, de esta posibilidad es de la que vamos a hablar, de qué manera se puede “materializar” el azar.

Esta proporción ha fascinado desde hace siglos al ser humano, que lo ha considerado un indicador de la perfección y la estética.

Para ello utilizaré un patrón “oculto” que hace ya tiempo descubrimos en la naturaleza, tratando de seguir su rastro para ver dónde nos lleva. Se trata de la “Proporción Áurea”, a veces denominada “Divina Proporción”.

La proporción áurea es perfecta cómo ejemplo para explicar todos estos aspectos tan contradictorios de la naturaleza y de paso entender la esencia de una teoría unificada. Esta relación puede describirse tanto de forma física como de forma matemática, es compatible con el criterio del azar y además representa un patrón organizado de comportamiento en sí misma. Es un patrón que además es independiente de la forma que tengamos de referirnos a él: es una proporción intemporal que ha existido siempre y siempre existirá. Si una civilización situada en el extremo opuesto del Universo la descubriera seguramente utilizaría una simbología completamente distinta de la nuestra, pero lo que nunca podría hacer es alterar su esencia. Se trata, por tanto, de un patrón tan universal cómo podría serlo la relación entre el diámetro y el arco de una circunferencia.

De acuerdo con el conocido físico y divulgador Paul Davies (la existencia de patrones intemporales de comportamiento)  “(…) implica que las leyes del Universo han diseñado su propia comprensión y que la mente y el conocimiento no son más que subproductos derivados de su evolución”. Si esto fuera cierto implicaría necesariamente que las leyes universales que conocemos no sólo gobiernan nuestra existencia, sino que también gobiernan nuestros pensamientos (Se trata del conocido “Pienso, luego existo”).  Este autor acaba su frase diciendo: “Esta es una asombrosa visión de la naturaleza, magnífica y estimulante en su majestuosa visión de conjunto. Espero que sea correcta. Sería maravilloso si fuera correcta. Pero si lo es, representaría un cambio en la cosmovisión científica tan profundo como el iniciado por Copérnico y Darwin juntos”.

Suele utilizarse el ejemplo de la reproducción de los conejos para explicar la proporción áurea, dado que fue el ejemplo que utilizó su descubridor, Fibonacci, para exponerla. Aunque serviría igual si utilizamos patos, seres humanos o partículas. Este pensador equiparó las virtudes matemáticas de la divina proporción con “Dios”, entre otros motivos porque en cualquier unidad de medida dada siempre habrá una proporción áurea implicada

Comencemos. Tomemos una pareja macho-hembra de conejos. Estos se encuentran, se gustan y sin más preámbulos llevan a cabo la fecundación. Al mes exacto del feliz encuentro dan a luz a una nueva pareja de conejos macho-hembra. Al final del primer mes, por tanto, tenemos dos parejas: una pareja adulta y una pareja de conejos bebe. Los conejos bebe han de esperar un mes para alcanzar la fertilidad y poder fecundar. La pareja adulta no se espera y el mismo día del feliz alumbramiento, haciendo honor a su fama, la hembra vuelve a quedarse preñada. Al final del segundo mes, por consiguiente, tenemos tres parejas: la pareja inicial, la pareja de bebes convertidos en adultos fértiles y la nueva pareja que acaba de nacer.

Si seguimos esta progresión al final del tercer mes tendremos 5 parejas, dos parejas adultas, una pareja que acaba de alcanzar la edad fértil, y dos parejas de bebes conejo que acaban de nacer. Al final del cuarto mes tendremos 8 parejas y así sucesivamente….

La relación que existe entre el número de parejas de un mes dado en comparación con el número de parejas del mes precedente es la que va componiendo progresivamente el valor que conocemos como proporción áurea o sucesión de Fibonacci (2/1, 3/2, 5/3, 8/5, 13/8, 21/13, etc….)  Cada vez que una pareja alcanza la edad adulta una nueva secuencia comienza y se “entrelaza” con la anterior generación en el tiempo.

Bueno… pues ¡Manos a la obra!….

Vamos a empezar a “descomponerla”…

Comencemos eliminando los conejos de la sucesión. Aunque sean prácticos en el ejemplo no son necesarios; Cualquier pareja de elementos con la capacidad de auto-duplicarse a sí misma nos serviría.

Sigamos eliminando conceptos innecesarios. Eliminemos el factor-tiempo. En el ejemplo hemos utilizado la magnitud “mes” como periodo de fertilidad o duplicación. Pero la sucesión no cambiaría su aspecto si en lugar de un mes fuera un día, un simple segundo o incluso si la duplicación fuera casi instantánea.

Ahora podemos observar más claramente la simplicidad de su comportamiento: “Pasado un cierto tiempo (sea el que sea) tiene lugar la aparición de un nuevo elemento”  ¡Ya está!, No hay más… ese es todo su “secreto”.

Parece sencillo ¿No es cierto? Pues bien, en la comprensión o el descubrimiento de este sencillo funcionamiento se asienta lo que conocemos como “mecánica cuántica”, basada en que cada cierto tiempo un electrón emite (de forma “espontánea”) un fotón. En terminología algo más técnica diríamos que las oscilaciones electromagnéticas se suceden de forma cuantificada (unitaria) y la energía implicada está directamente relacionada con la frecuencia.

¿Cada cuánto tiempo sucede esto? Lo cierto es que es difícil responder a esta pregunta porque no tenemos manera de cuantificar este suceso. Sabemos que ocurre de forma “casi” instantánea  (si lo observamos a escala humana) pero no hay forma ni manera de establecer un criterio objetivo basado en el tiempo.

La única manera paralela que tenemos de hacerlo no es utilizando un criterio basado en el tiempo, sino utilizando un criterio basado en la frecuencia o la probabilidad. Si tenemos 137 electrones uno de ellos emitirá espontáneamente un fotón; Dicho de otra manera, la probabilidad de que se emita un fotón en un instante dado de tiempo es 1/137. A este cociente lo llamamos “Constante de estructura fina” y se trata de la constante más representativa de toda la física conocida.  Aunque no lo parezca a primera vista este cociente es el resultado de mezclar tres constantes fundamentales de la naturaleza: la velocidad de la luz, la constante de Planck y la carga del electrón. Lo más sorprendente de esta constante es que no viene definida por ninguna unidad física de medida, es un simple número… ¡Sin más!

   Sí, parece que todo es una aventura en el Universo

A veces se denomina “Constante de acoplamiento universal” y nos proporciona una referencia de lo milimétricamente diseñado que está el Universo, pues si su valor cambiara ligeramente no existiría el Universo cómo lo conocemos. Dada su independencia respecto del tiempo, su esencia continua inalterada: cada cierto tiempo algo pasa dentro del electrón y el resultado es que se emite (o absorbe) un  fotón. Esta constante (como vemos) conserva la misma esencia en que se basa la divina proporción.

A esta actividad (no sabemos si frenética o no) que tiene lugar en los núcleos atómicos a veces se le denomina “Energía del vacío” (la energía que surge de la nada,  la “Chispa de la Creación”) y básicamente implica que toda partícula en el Universo tiene literalmente una especie de” vida interior”, una vida que se expande en base a este movimiento de duplicación y que es el germen primigenio de lo que denominamos “Expansión del Universo”. Como sabemos gracias a Edwin Hubble el Universo se está expandiendo, lo que implica que las galaxias se alejan unas con respecto de las otras desde el principio de los tiempos. A veces decimos que la expansión del Universo no tiene sentido físico, dado que no sabemos lo que implica que tanto el espacio como el tiempo se estén creando en este mismo momento.

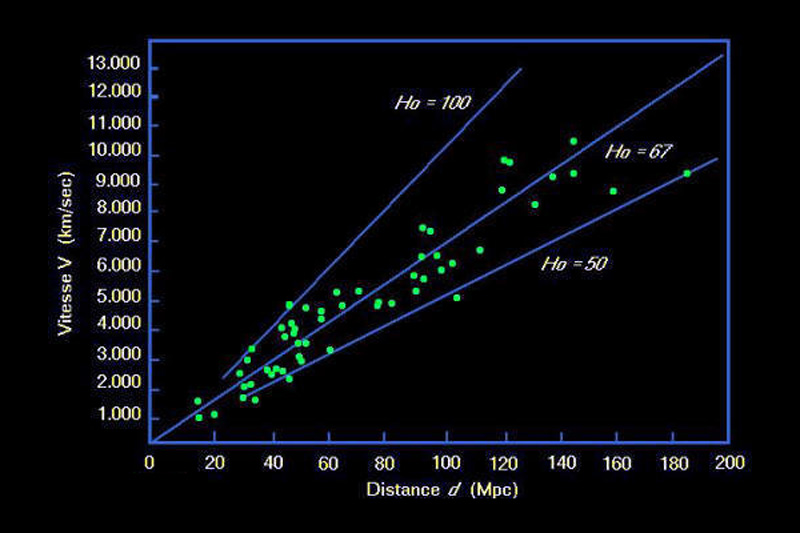
La imagen original era más atractiva pero, la página no la aceptó

Pero lo más sorprendente no es que este movimiento duplicativo o expansivo no tenga sentido físico, lo más sorprendente es que tan sólo podamos definirlo en base a relaciones numéricas. Pero incluso en este sentido este comportamiento guarda una extraña y misteriosa correlación con la “divina proporción” pues este patrón se basa también única y exclusivamente en relaciones numéricas.

Heisenberg, quien formuló la ley fundamental de la mecánica cuántica (que básicamente establece que un estado cuántico es indeterminado) solía decir que los átomos no son cosas, sino que son “tendencias”  ¿Podemos aplicar también esta idea a nuestra mágica proporción? Pues resulta que sí, que también podemos hacerlo.

Aunque parezca paradójico la divina proporción es un teorema matemático (en el sentido de que sigue una regla de comportamiento) y no lo es al mismo tiempo.  Un teorema podemos definirlo como una regla estática de equilibrio; Sin embargo dicha proporción es una regla dinámica, un valor que se va aproximando a él mismo a medida que vamos añadiendo más y más decimales a su valor. La divina proporción representa una tendencia, siendo ésta además una tendencia indeterminada, dado que se trata de una sucesión que nunca se acaba. De forma matemática la proporción áurea es una imposibilidad pero, sin embargo… ¡Ahí está!

                  Max Planck

Max Planck decía que: “La materia se origina y existe sólo en virtud de una fuerza que hace vibrar las partículas del átomo” refiriéndose a éste como el más diminuto de los sistemas solares. Poco tiempo después de sus descubrimientos los físicos comprendieron que las matemáticas que describen las frecuencias del sonido emitido por un tambor podían usarse también para calcular los niveles energéticos de vibración de los electrones en un átomo. El problema era descifrar la forma del tambor matemático que determinaba esos niveles energéticos del núcleo.  La sorpresa fue descubrir que una función matemática creada por Riemann para tratar de cartografiar la distribución de los números primos coincidía a la perfección con las distribuciones que ellos buscaban. Resultaba que los “átomos de los números” y los “átomos de la materia” se encontraban sometidos a la misma distribución o a la misma estructura.

Cuando decimos que un patrón (matemático o no) es intemporal o independiente del tiempo también solemos referirnos a este hecho diciendo que la información que transmite tan sólo existe en un tiempo imaginario, una especie de plano temporal que opera en una dimensión no-material.  El mejor ejemplo para describir esto lo encontramos en el teorema más famoso de la humanidad: el  “Teorema de Pitágoras”. Dicho teorema, al margen de las aplicaciones prácticas que todos conocemos, establece una especie de verdad inmutable y universal: “Siempre que tengamos dos elementos absolutamente opuestos entre ellos, dichos elementos estarán relacionados”.

En el caso de la divina proporción esto no sólo es cierto, sino que dicha relación por si sola ya define la misma relación en que se basa el Teorema de Pitágoras. Y es que la divina proporción es el único valor matemático cuyo valor y su valor opuesto resultan ser el mismo valor; Algo aparentemente imposible, pero cierto.

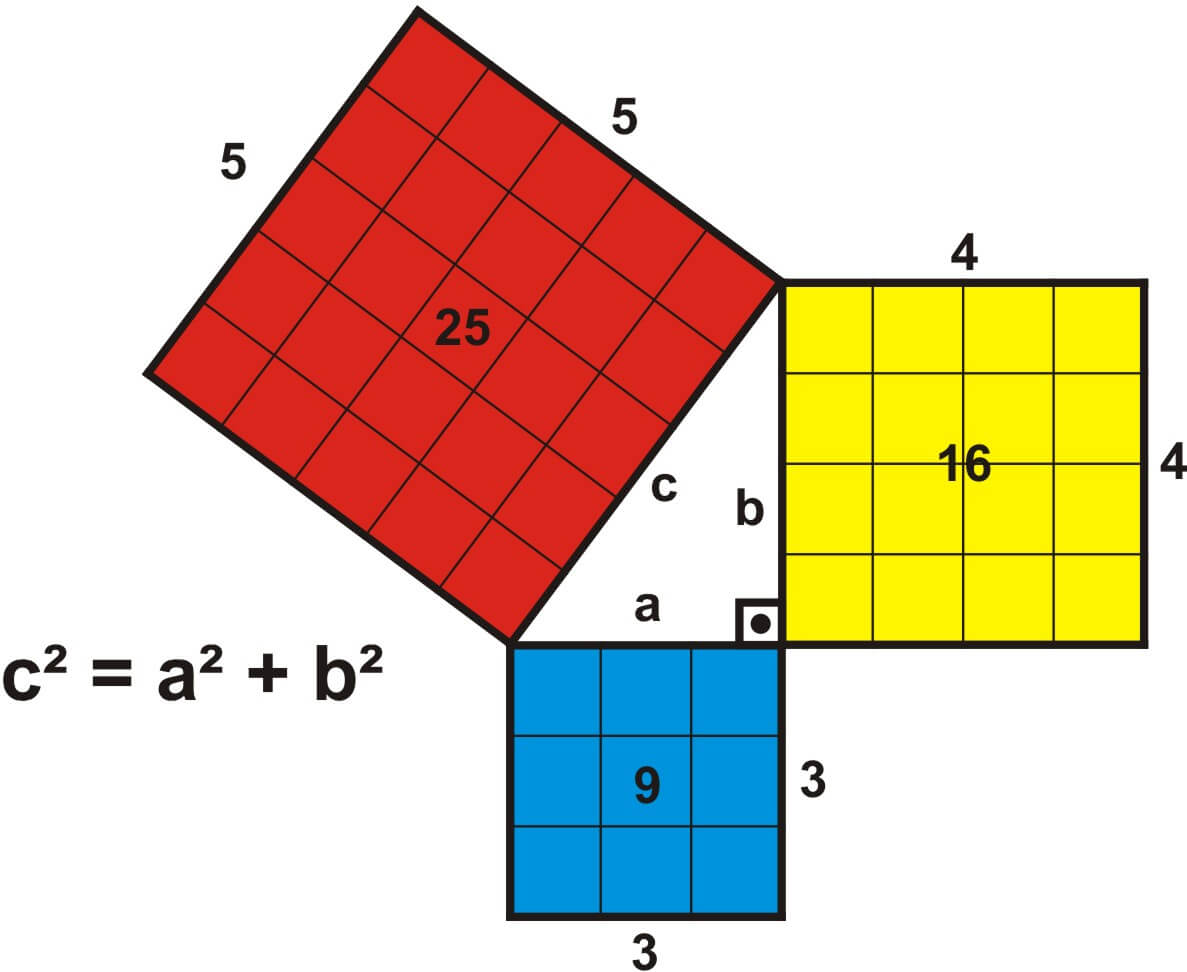
El Teorema de Pitágoras es muy especial. No sólo por ser el único criterio capaz de unificar toda la geometría conocida, sino porque constituye la única regla de Entrelazamiento Dimensional entre dos elementos conocida en matemáticas. Es lo que se conoce como “Conjetura de Fermat” que (básicamente) establece que en el Universo matemático tan sólo es posible relacionar dos elementos opuestos entre ellos cuando los elevamos al cuadrado. Esta propiedad  tan sorprendente es la base de lo que conocemos como “Ley de la Gravedad”, que dictamina que dos elementos tan opuestos entre ellos como son las masas y las distancias que las separan coinciden en una dimensión diferente: la dimensión de los cuadrados de sus elementos.

De hecho, la relación de los cuadrados está presente en todos lados donde hemos podido encontrar un patrón de comportamiento. La ondulatoriedad en mecánica cuántica se basa en el cuadrado absoluto de la función de onda,  la fuerza electromagnética se debilita en proporción inversa al cuadrado de la distancia entre dos fuerzas eléctricas; Incluso los planetas dan vueltas alrededor del Sol en tiempos cuyos cuadrados son iguales a los cubos de sus distancias.

Pero… ¿Qué sentido físico tiene la elevación al cuadrado? Lo cierto es que tampoco lo sabemos porque queda literalmente en una dimensión diferente. Nuestra capacidad de captar el mundo a través de los sentidos es lineal, de la misma forma que lo es nuestra forma de pensar. No podemos pensar en dos cosas al mismo tiempo y por este motivo la única operación lógica que puede hacer nuestro cerebro es “triangular”.

Las coincidencias son sorprendentes. La proporción áurea es el único valor que incorpora automáticamente una dimensión matemáticamente posible, pero físicamente inexistente. Se trata de un valor doblemente irracional, no tan sólo por incorporar el infinito en su formulación, sino por incorporar también el plano imaginario, que es precisamente el plano que da sentido a la descripción probabilística del mundo a nivel cuántico o fundamental.

Como indican los controvertidos físicos y gemelos Bodganov: “Los grandes teóricos de los números están convencidos: en el corazón de estas series interminables, en esos miles de millones de cifras que giran en el infinito hay un secreto. Una clave que, abriendo las puertas del infinito, nos hace regresar al cero. Y por tanto a la creación del Universo”.

No podría estar más de acuerdo. Es más, creo que es cierto y que existe una demostración maravillosa al respecto. A fin de cuentas, si es cierto que el Universo se basa en la probabilidad, tan sólo es cuestión de tiempo que lo imposible se haga realidad.

Ricard Jiménez