Dic
31
La Física no duerme
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)

Lentes atómicas
Científicos del DIPC y el Centro de Física de Materiales (CSIC-UPV) y de la Universidad de Cambridge, han creado una lente que puede concentrar la luz en dimensiones inferiores a las de un átomo. Los investigadores han utilizado nanopartículas de oro para desarrollar estas lentes focalizadoras, que permiten ver enlaces químicos individuales en las moléculas.

Nuestras predicciones teóricas sugerían que esto podía ser posible, como así se ha comprobado ahora, asegura el profesor Javier Aizpurua, que lidera los esfuerzos teóricos de esta investigación, y cuyo desarrollo ha permitido entender el confinamiento y la interacción de la luz con moléculas en escalas tan pequeñas.
El equipo de investigadores experimentales de Cambridge, liderado por el profesor Jeremy Baumberg, ha utilizado oro altamente conductor para fabricar la cavidad óptica más pequeña del mundo (picocavidad), que confina la luz a una distancia inferior a una mil millonésima de metro.
Los resultados se han publicado en Science.
Fuente: Revista mensual electrónica de la Real Sociedad Española de Física.
Dic
27
Las misteriosas funciones modulares
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Rumores del saber del mundo ~
Clasificado en Rumores del saber del mundo ~
 Comments (0)
Comments (0)

Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.
Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del Este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro Universo actual.
El misterio de las Funciones Modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él trabajó en total aislamiento, en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que, los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
La función modular de Ramanujan y la teoría de cuerdas
![]()
La función de Ramanujan contiene un término elevado a la potencia veinticuatro. Ese número es el origen de las cancelaciones milagrosas que se dan en la … Pero hablemos de las cuerdas.
La teoría de cuerdas supone que cada modo o vibración de una cuerda fundamental representa una partícula elemental distinta, y puede explicar a la vez la naturaleza de la materia y del espacio-tiempo (las partículas en lugar de ser puntuales pasan a ser unidimensionales). Es la primera teoría cuántica de la gravedad: Cuando se calcularon por primera vez las ligaduras de autoconsistencia que impone la cuerda sobre el espacio-tiempo, se observó con sorpresa que las ecuaciones de Einstein ( teoría de la gravedad) emergían de la cuerda, de hecho, el gravitón o cuanto de gravedad era la menor vibración de la cuerda cerrada.
No sabemos todavía por qué la teoría de cuerdas está definida sólo en 10 y 26 dimensiones, aunque parece seguro que esta teoría no podría unificar las fuerzas fundamentales con tan solo tres dimensiones. Las cuerdas se rompen y se forman en el espacio N-dimensional arrastrando con ellas una serie de términos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos aparecen multiplicados por el factor (N-10), lo que nos obliga a elegir N=10 para eliminarlos.

Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre los más extraños jamás encontradas en matemáticas. Ellos reaparecen en los ramos más distantes e inconexos de las matemáticas. Una función, que aparece una y otra vez en la teoría de las funciones modulares, se denominan (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.
El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente, donde menos se esperan, por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. (Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio -tiempo debe tener 24 + 2 = 26 dimensiones espacio – temporales.)

Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. No estará la solución final de la Teoría de cuerdas, en estas misteriosas funciones modelares.
Para comprender este misterioso factor de dos (que añaden los físicos consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.
Antes explicamos que cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio – tiempo sea diez.

Claro que, la Teoría de Cuerdas tiene versiones en 10, 11 y 26 dimensiones
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “No lo se”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por que se seleccionan estos números concretos.
Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.
Srinivasa Ramanujan nació en 1.887 en Erode, India, cerca de Madrás. Su familia de clase media alta, brahmin, la más alta de las castas Hindúes, fueron destituidos y venidos a menos, su padre trabajaba de oficinista de un comerciante de tejidos.
Con diez años, lo mismo que pasó antes con Riemann, ya destacaba y sorprendía a todos con sus enormes poderes de cálculos. Siendo niño, rederivó la identidad de Euler entre funciones trigonométricas y exponenciales.

En la vida de cada científico joven hay un punto de partida, un hecho que, sin ellos saberlo, les marca el destino. Para Einstein fue la fascinación que le causó la brújula que le regaló su tío cuando estaba enfermo siendo un niño, no podía apartar la mirada de la aguja que siempre indicaba hacia el mismo sitio, y se preguntó una y mil veces por la fuerza invisible que la obligaba a dirigirse hacia esa dirección. Para Riemann, fue la lectura del libro de matemáticas de Legendre. Para Ramanujan, fue cuando se sumergió en un oscuro y olvidado libro de matemáticas escrito por George Carr. Este libro ha quedado inmortalizado desde entonces por el hecho de que señaló la única exposición conocida de Ramanujan a los modernas matemáticas occidentales. Según su hermana: “Fue este libro el que despertó su genio. El se propuso establecer por sí mismo las fórmulas dadas allí. Como no tenía la ayuda de otros libros, cada solución era un trabajo de investigación por lo que a él concernía… Ramanujan solía decir que la diosa Namakkal le inspiraba las fórmulas en sueños”.

Con ayuda de amigos, Ramanujan consiguió un puesto de bajo nivel del puerto de Madrás. Era un trabajo servil, con una mísera paga de 20 libras al año, pero dio libertad a Ramanujan, como a Einstein antes que él en la oficina de Patentes Suiza, para seguir sus sueños en su tiempo libre. Ramanujan, en la fascinación que en él ejercían los números, era incansable, llenaba libretas enteras de cálculos y ecuaciones que antes veía florecer en su cabeza.
Así estaban las cosas cuando decidió escribir algunos de sus trabajos a las tres matemáticos más famosos de Inglaterra y Europa.
Dos de aquellos matemáticos, al tener en su poder las cartas enviadas por un miserable empleado sin instrucción formal alguna, sin haber comprobado su contenido, las arrojaron directamente a la basura. El tercero era el brillante matemático de Cambridge Godfrey Harold Hardy. Debido a su categoría en Inglaterra, Hardy estaba acostumbrado a recibir correo de chiflados proponiéndole los más peregrinos proyectos y, en un primer momento apenas prestó atención a la carta del joven Ramanujan.
Srinivasa Ramanujan trabajó principalmente en teoría de números, encontrando identidades relacionadas con el número pi y el número e o los números primos. Como decimos, en general sus fórmulas son muy enrevesadas, pero en su mayoría verdaderas (a posteriori se ha descubierto que algunos de sus resultados era incorrectos), y algunas de ellas se han convertido en potentes herramientas para calcular grandes cantidades de decimales de, principalmente, el número pi. Quizás la más conocida sea ésta:
que nos da 8 decimales exactos de pi en cada iteración. Tremendo, ¿verdad?
Entre los densos garabatos advirtió muchos teoremas matemáticos que ya eran bien conocidos. Pensando que era la obra obvia de un plagiario, el también la desechó en ese primer impulso. Pero había algo que no encajaba. Algo que inquietaba a Hardy; no podía dejar de pensar en aquella extraña carta.
Durante la cena de esa noche, 16 de enero de. 1913, Hardy y su colega John Littlewood discutieron esta carta singular y decidieron echar un segundo vistazo – repaso a su contenido. Comenzaba de forma bastante inocente, con “Me permito presentarme a usted como un empleado en el departamento de contabilidad de la oficina del puerto franco de Madrás con un salario de solo veinte libras al año”. Pero la carta del pobre empleado de Madrás contenía teoremas que eran totalmente desconocidos para los matemáticos occidentales. En total, contenía 120 teoremas. Hardy estaba atónito. Recordaba que demostrar algunos de esos teoremas “Me derrotó por completo”. “Nunca había visto nada antes que se le pareciera en lo más mínimo. Una simple ojeada a ellos es suficiente para mostrar que sólo podían estar elaborados por un matemático muy grande”.
Littlewood y Hardy alcanzaron la misma conclusión: Aquello era el trabajo de un genio empeñado en derivar de nuevo 100 años de matemáticas europeas. “Él había estado llevando a cabo una carrera imposible, un pobre y solitario hindú, completamente solo y sin ayuda, enfrentando su cerebro contra toda la sabiduría acumulada en Europa”, recordaba con asombro Hardy.

Hardy escribió a Ramanujan y, tras muchas pesquisas, uso de amistades e influencias, arregló su estancia en Cambridge en 1.914. Por primera vez, Ramanujan podía comunicarse regularmente con sus iguales, la comunidad de los matemáticos europeos. Entonces comenzó el estallido de su actividad: tres cortos e intensos años de colaboración con Hardy en el Trinity Collage en Cambridge.
Hardy trató más tarde de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido como uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando este diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló: “Parecía ridículo importunarle sobre como había descubierto este o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi número 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable como una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y también la suma de 9 x 9 x 9 y 10 x 10 x 10).

Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el nombre de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Si finalmente las dos madejas se desenredan… ¡Por algo será!
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.
En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas. Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión. El enunciado correcto sería ahora: las leyes de la naturaleza se simplifican cuando se expresan COHERENTEMENTE en dimensiones más altas. El añadido de la palabra coherente es crucial. Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo. Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.
Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.
¿La décima dimensión?
¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?
Steven Weinberg
emilio silvera
El apunte sobre Ramanujan fue incluido en otro de mis trabajos. Sin embargo, el presente cuaderno trata temas expresamente solicitados para utilizar en unos seminarios de física, y se me pidió incluir el tema “Ramanujan”. La Fuente es diversa y precisaría una larga relación.
Dic
27
Buscando nuevas teorías
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Nuevas revoluciones científicas ~
Clasificado en Nuevas revoluciones científicas ~
 Comments (3)
Comments (3)

El holandés Erik Verlinde acaba de provocar un pequeño terremoto al decir que la materia oscura no existe y cuestionar a Einstein y su teoría de la relatividad. La propuesta de este físico teórico de la Universidad de Ámsterdam ha despertado las suspicacias entre algunos de sus colegas, mientras otros reconocen que su idea es interesante.

La inmensa mayoría de expertos piensa que las leyes formuladas por Isaac Newton hace más de tres siglos y la relatividad aportan la mejor explicación del universo, y la inmensa mayoría de observaciones y experimentos hasta la fecha, incluidas las ondas gravitacionales descubiertas este mismo año, les da la razón. Sin embargo estas teorías no sirven en el mundo de lo muy pequeño, donde las interacciones entre las partículas elementales están gobernadas por la teoría cuántica de campos, incompatible con la relatividad. También en el universo a grandes escalas, en galaxias, grupos de galaxias y los cúmulos con decenas o cientos de galaxias, la gravedad es mucho más fuerte de la que ejerce la materia visible. Para que las ecuaciones de Einstein funcionen en estos entornos es necesario añadir el empuje gravitatorio de la invisible materia oscura y la fuerza de la energía oscura, que acelera la expansión del universo. Juntos, estos dos ingredientes desconocidos suponen el 95% del universo.
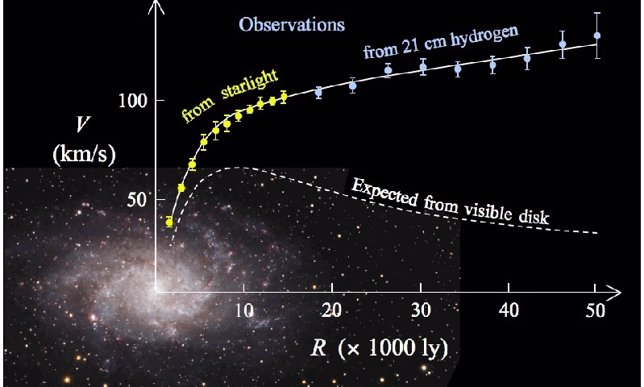
Una nueva teoría de la gravedad podría explicar la materia oscura
La nueva teoría de la gravedad emergente podría explicar el curioso movimiento de las estrellas en las galaxias, según el experto en teoría de cuerdas Erik Verlinde, de la Universidad de Amsterdam. Esta ‘segunda ley de Newton’ predice exactamente la misma desviación de los movimientos que se suele explicar cuando se inserta la materia oscura en la teoría.
La propuesta de Verlinde afirma que la fuerza de la gravedad entre dos objetos muy distantes decae menos de lo que predijeron Newton y Einstein. De esta forma, solo el empuje de la materia visible y la interacción con la energía oscura bastan para explicar el comportamiento de las galaxias.
Un equipo de astrónomos de Holanda, Alemania, Reino Unido y Australia ha puesto a prueba esta teoría en observaciones de más de 33.000 galaxias. Sus conclusiones son que tanto la teoría de Verlinde como la de Einstein sirven para explicar la curvatura de la luz por la gravedad. Pero las ecuaciones de Verlinde, resaltan los autores, explican esa distorsión sin necesidad de materia oscura.
“El resultado de esta primera prueba parece definitivamente interesante”, ha dicho Margot Brower, astrónoma del Observatorio de Leiden y coautora del estudio, publicado online en Monthly Notices of the Royal Astronomical Society. “Ahora la pregunta es si esta nueva teoría sigue adelante y si se puede probar” a mayor escala.
Árboles en medio del mar
Como teórico de cuerdas,el trabajo del holandés intenta conjugar la naturaleza cuántica de la realidad con los conceptos de espacio y tiempo de Einstein, usando una sola teoría, un logro que sería más importante que la relatividad. “Lo que propone Verlinde es que la energía oscura revela que hay un entrelazamiento cuántico de larga distancia cuyo efecto sería modificar las ecuaciones de la gravitación clásicas a grandes distancias”, explica José Luis Barbón, investigador del Instituto de Física Teórica, en Madrid. “Los físicos vemos la gravitación desde Einstein como una deformación del espacio-tiempo, pero aquí la idea es que la elasticidad intrínseca del espacio es diferente de la habitual cuando te vas a distancias muy grandes, debido a ese entrelazamiento de larga distancia”, añade.

El argentino Juan Maldacena, uno de los físicos teóricos en cuyas ideas se ha inspirado Verlinde, destruye a su colega con una analogía. “Los astrofísicos son como un navegante […] que va en el medio del océano” y de repente se encuentran ramas de árboles, señala. “La teoría de la materia oscura es análoga a concluir que debe haber una isla cerca, mientras que la teoría de Verlinde es análoga a decir: ‘Oh, hay algas con forma de ramas de árboles que crecen en el mar” . “Creo que es tan probable que su teoría sea cierta como que haya árboles que crecen en el medio del mar”, remacha este físico teórico del Instituto de Estudio Avanzado de Princeton, EE UU.

Mordehai Milgrom
Mordehai Milgrom, del Instituto Weizmann, en Israel, dice que el trabajo es “muy bienvenido”, porque ayuda a atraer a científicos de disciplinas como la teoría de cuerdas al desarrollo de alternativas a la relatividad. Pero considera que la idea de Verlinde es aún “muy preliminar” y “está muy lejos de haber resuelto el problema de la materia oscura con una teoría fundamental elegante”. Milgrom desarrolló en los 80 la dinámica newtoniana modificada (MOND, en sus siglas en inglés), que también niega que exista la materia oscura. En su opinión, la teoría de Verlinde es una derivada parcial de su propio trabajo, al que además el físico holandés no habría reconocido como debe.

Todas estas teorías alternativas “naufragan bastante” cuando intentan describir el universo a escalas mayores, como los cúmulos de galaxias, así como la estructura detallada de la radiación de fondo radiación de fondo de microondas tras el Big Bang, advierte Barbón. “Las ideas de Verlinde son interesantes, pero muy vagas”, explica. “Es enteramente posible que sean totalmente erróneas, aunque también es posible que encierren algo de verdad, en este momento son demasiado nebulosas como para emitir un veredicto”, señala.
Verlinde no ha respondido a las preguntas de Materia. En un video facilitado por la Universidad de Ámsterdam, dice que la manera de falsar su propuesta es “descubrir una partícula que describa” el comportamiento de la gravedad “en galaxias y grupos de galaxias”, algo que, por ahora, nadie ha logrado
Dic
23
El descubrimiento del siglo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Ondas gravitacionales ~
Clasificado en Ondas gravitacionales ~
 Comments (0)
Comments (0)
KIP THORNE, el físico experto en Agujeros Negros que vaticinó el hallazco de las Ondas Gravitacionales y fue también, el impulsor del Programa LIGO para localizarlas.
Reportaje de Prensa
La revista ‘Science’ elige las ondas gravitacionales como el hallazgo más relevante de 2016. La autora de este texto es la jefa del único grupo español en el experimento LIGO
No me cabe la menor duda que 2016 será un año que difícilmente olvidaré. Este ha sido un año de grandes avances científicos en muchos campos y de importantes descubrimientos, pero, entre todos ellos, uno ha sido muy especial para mí y mis colaboradores: las primeras observaciones de ondas gravitacionales con LIGO.
Desde que el pasado 11 de febrero, después de minuciosos análisis, las colaboraciones científicas LIGO y Virgo anunciaran la primera detección directa de ondas gravitacionales y la primera observación de la fusión de un sistema binario de agujeros negros, las desconocidas ondas gravitacionales han acaparado la atención de los medios y de la mayoría de los más prestigiosos premios internacionales. Esto no es de extrañar, ya que estas primeras detecciones directas de ondas gravitacionales han sido sin duda uno de los logros científicos más importantes del siglo, no solo porque han servido para validar uno de los pilares de la física moderna, la teoría de la relatividad general, precisamente en su centenario, sino también porque se abre una nueva ventana desde la que observar al Universo, con el potencial de descubrir sistemas astronómicos ahora inimaginables.

Programa LIGO

¿Qué duda nos puede caber? Ha sido un gran paso para conocer de manera diferente el Universo
Estas primeras detecciones directas de ondas gravitacionales han servido para validar uno de los pilares de la física moderna, la teoría de la relatividad general, y también se abre una nueva ventana desde la que observar al Universo
La historia de los detectores de ondas gravitacionales se remonta a los años 60. Aún así la búsqueda de ondas gravitacionales no ha hecho más que empezar. En los próximos años, a medida que los detectores avanzados LIGO y Virgo se acerquen a su sensibilidad de diseño, observaremos de forma regular algunos de los fenómenos más energéticos y violentos del universo. Lo que será decisivo en el avance de la física fundamental, astrofísica y cosmología, permitiéndonos explorar importantes cuestiones, como por ejemplo cómo se forman los agujeros negros, si la relatividad general es la descripción correcta de la gravedad, o cómo se comporta la materia bajo condiciones extremas. En un futuro, nuevas generaciones de detectores permitirán hacer astronomía de alta precisión, como por ejemplo el detector europeo “Einstein Telescope” o el observatorio de la Agencia Espacial Europea “LISA”, que podrían empezar a operar en la década de los 30.

En estos momentos, los detectores LIGO vuelven a estar operando en modo de observación, aunque su funcionamiento se interrumpirá durante las vacaciones. Todos nosotros estamos ansiosos y preparados para que la naturaleza nos sorprenda de nuevo y poderlo contar. Pero parece claro que este año no habrá ninguna alerta el día de Navidad.
Alicia Sintes es investigadora principal del grupo de la colaboración científica LIGO en la Universitat de les Illes Balears
Dic
17
¡Las estrellas! Algo más que puntitos brillantes en el cielo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en las estrellas y la Vida ~
Clasificado en las estrellas y la Vida ~
 Comments (0)
Comments (0)


“¿Está el Corazón y el Alma de nuestra Galaxia localizadas en Casiopeia? Posiblemente no, pero ahí es donde dos brillantes nebulosa de emisión apodadas Corazón y Alma descansan. La Nebulosa del Corazón, oficialmente catalogada como IC 1805 y visible en la parte superior derecha, tiene una forma en luz visible que nos recuerda a un clásico símbolo de un corazón. La imagen de arriba, sin embargo , fue realizada en luz infrarroja por el recientemente lanzado telescopio WISE. La luz infrarroja penetra bien dentro de las enormes y complejas burbujas creadas por la formación estelar en el interior de estas dos regiones de formación de estrellas.
Los estudios de estrellas y polvo como éstos encontrados en las Nebulosas Corazón y Alma se han focalizado en cómo se forman las estrellas masivas y cómo les afecta su entorno. La luz tarda unos 6.000 años en llegarnos desde estas nebulosas, que juntas abarcan unos 300 años luz.” (APOD)
Ubicadas en el brazo de Perseo de nuestra galaxia, la nebulosa Corazon (derecha) y la nebulosa Alma (izquierda) son muy brillantes (a pesar de eso es necesario un telescopio para verlas) en una region de la galaxia donde muchas estrellas se estan formando. IC 1805 (la nebulosa Corazon) es a menudo llamada tambien como la nebulosa del Perro Corriendo, debido obviamente a la apariencia de la nebulosa vista desde un telescopio.

Es curioso que, mirando en la oscura noche como brillan las estrellas del cielo, nos atrae su titilar engañoso (es la atmósfera terrestre la que hace que lo parezca) y su brillo, Sin embargo, pocos llegan a pensar en lo que verdaderamente está allí ocurriendo. Las transformaciones de fase por fusión no cesan. Esta transformación de materia en energía es consecuencia de la equivalencia materia-energía, enunciada por Albert Einstein en su famosa fórmula E=mc2; donde E es la energía resultante, m es la masa transformada en energía, y c es la velocidad de la luz (300 000 kilómetros por segundo). La cantidad de energía que se libera en los procesos de fusión termonuclear es fabulosa. Un gramo de materia transformado íntegramente en energía bastaría para satisfacer los requerimientos energéticos de una familia mediana durante miles de años.

Imagen de Sirio A (estrella grande) y Sirio B (estrella pequeña abajo a la izquierda) tomadas por el Telescopio Hubble (Créd. NASA). Sirio es la quinta estrella más cercana y tiene una edad de 300, millones de años. Es una estrella blanca de la secuencia principal de tipo espectral A1V con temperatura superficial de 10 000 K y situada a 8,6 años luz de la Tierra. Es una estrella binaria y, de ella, podríamos contar muchas historias. La estrella fue importante en las vidas de Civilizaciones pasadas como, por ejemplo, la egipcia.
Lo que conocemos como estrella es una bola de gas luminosa que, durante una etapa de su vida, produce energía por la fusión nuclear del hidrógeno en helio. El término estrella, por tanto, no sólo incluye estrellas como el Sol, que están en la actualidad quemando hidrógeno, sino también protoestrellas, aún en formación y no lo suficientemente calientes como para que dicha combustión nuclear haya comenzado, y también varios tipos de objetos más evolucionados como estrellas gigantes y supergigantes, que están quemando otros combustibles nucleares, o las enanas blancas y las estrellas nucleares, que están formadas por combustible nuclear gastado.

Seguimos en la Nebulosa del Corazón (otra región)
Las estrellas se forman a partir de enormes nubes de gas y polvo que a veces tienen hasta años-luz de diámetro. Las moléculas de polvo, unidas a las de los gases, se rozan y se ionizan, se calientan y la nube comienza a girar lentamente. El enorme conglomerado, poco a poco se va juntando y la temperatura aumenta. Tal enormidad de materia crea una fuerza gravitatoria que hace contraerse la nube sobre sí misma; su diámetro y su temperatura en el núcleo es tal que se produce la fusión de los protones de hidrógeno que se transforman en un material más complejo, el helio, y ese es el momento en que nace la estrella que, a partir de ahí, puede estar miles de millones de años brillando y produciendo energía termonuclear.
La masa máxima de las estrellas puede rondar las 120 masas solares, es decir, ser 120 veces mayor que nuestro Sol, y por encima de este límite sería destruida por la enorme potencia de su propia radiación. La masa mínima para poder ser una estrella se fija en 0’08 masas solares; por debajo de ella, los objetos no serían lo suficientemente calientes en sus núcleos como para que comience la combustión del hidrógeno y se convertirían en enanas marrones. Las luminosidades de las estrellas varían desde alrededor de medio millón de veces la luminosidad del Sol para las más calientes hasta menos de la milésima de la del Sol para las enanas más débiles. Aunque las estrellas más prominentes visibles a simple vista son más luminosas que el Sol, la mayoría de las estrellas son en realidad más débiles que éste y, por tanto, imperceptibles a simple vista.

La estrella Sirio es la más brillante y tiene el doble de tamaño que nuestro Sol


Eta Carinae (NGC 3372) tiene 400 veces el diámetro del Sol inmersa en esa Nebulosa que la esconde dentro del gas y el polvo-

Betelgeuse tiene 1.000 veces el díametro de nuestro Sol
Pero la estrella más grande conocida es:

VY Canis Majoris, supergigante roja que es aproximadamente 2.100 veces más grande que nuestro Sol.
El brillo de las estrellas (la luz y el calor) es el resultado de la conversión de masa en energía (E = mc2), por medio de reacciones nucleares, las enormes temperaturas de millones de grados de su núcleo, hace posible que los protones de los átomos del hidrógeno se fusionen y se conviertan en átomos de helio. Por cada kilogramo de hidrógeno quemado de esta manera, se convierten en energía aproximadamente siete gramos de masa. De acuerdo con la famosa ecuación de Einstein (arriba reseñada), los siete gramos equivalen a una energía de 6’3 × 1014 julios. Las reacciones nucleares no sólo aportan la luz y el calor de las estrellas, sino que también producen elementos pesados, más complejos que el hidrógeno y el helio que, posteriormente, son distribuidos por el universo, cuando al final de la estrella, esta explota en supernova, lanzando sus capas exteriores al espacio que de esta forma, deja “sembrado” de estos materiales el “vacio” estelar.
Las estrellas pueden clasificarse de muchas maneras. Una manera es mediante su etapa evolutiva: en presecuencia principal, secuencia principal, gigante, supergigante, enana blanca, estrella de neutrones y agujeros negros. Estas últimas son la consecuencia del final de sus vidas como tales estrellas, convirtiéndose en objetos estelares de una u otra clase en función de sus masas originales. Estrellas como nuestro Sol, al agotar el combustible nuclear se transforman en gigantes rojas, explotan en novas y finalmente quedan como enanas blancas. Si la masa es mayor serán estrellas de neutrones, y si aún son mayores, su final está en agujeros negros.

Nuestro Sol, nos parece un objeto enorme, grandioso que, es capaz, con su actividad de enviar a la Tierra luz y calor (radiación) para que podamos vivir los seres que la pueblan. Sin embargo, a pesar de su “grandeza”, la comparamos con otros objetos celestes y, desde luego, nos podemos quedar asombrados de que puedan existir cosas tan grandes como VY Canis Majoris. Podéis observar en ellas su tamaño en comparación con nuestro Sol.
El Color de las estrellas indican de qué materiales están conformadas y, así se compruena mediante el estudio de sus espectros.
- Color azul, como la estrella I Cephei
- Color blanco-azul, como la estrella Spica
- Color blanco, como la estrella Vega
- Color blanco-amarillo, como la estrella Proción
- Color amarillo, como el Sol
- Color naranja, como Arcturus
- Color rojo, como la estrella Betelgeuse.
Otra clasificación es a partir de sus espectros, que indican su temperatura superficial. También por el color. Otra manera es en poblaciones I, II y III, que engloban estrellas con abundancias progresivamente menores de elementos pesados, indicando paulatinamente una mayor edad. También evolución estelar y magnitudes aparentes y absolutas y el tipo espectral con la distancia en a. L., es otra de las clasificaciones.
Después de estas clasificaciones genéricas tenemos otras mas particulares y definidas referidas a estrellas binarias, estrellas capullo, con baja velocidad, con envoltura, con exceso de ultravioleta, de alta velocidad, de baja luminosidad, de baja masa, de bario, de bariones, de campo, de carbono, de circonio, de estroncio, de helio, estrella de la población I extrema, de la población intermedia, de la rama gigante asintótica, estrella de litio, de manganeso, de manganeso-mercurio y, viceversa, estrella de metales pesados, de neutrones, estrellas de quarks (hipotética con densidad intermedia entre la estrella de neutrones y el agujero negro), estrella de referencia, de silicio, de tecnecio, de tiempo intermedio, de tipo tardío, de tipo temprano, estrella del polo, estrella doble, estrella enana, estándar, evolucionada, etc.
La luz proveniente de la superficie caliente del Sol pasa a través de la atmósfera solar más fría, es absorbida en parte, por eso llega a nosotros presentando las características líneas oscuras en su espectro. Las líneas oscuras del espectro del sol coinciden con líneas de los espectros de algunos elementos y revelan la presencia de estos elementos en la superficie solar. Las longitudes de onda de las radiaciones se indican en nanometros (nm).
El Sol

De qué está hecho el Sol
La posición e intensidad de las líneas oscuras del espectro solar han permitido establecer que casi las tres cuartas partes de la masa del Sol son hidrógeno, el elemento más simple. Casi todo el resto es helio, el segundo elemento más simple. En suma, entre hidrógeno y helio suman alrededor del 98 por ciento de la masa solar. El 2% restante está compuesto, aproximadamente, por la siguiente proporción de elementos: 0,8% de oxígeno, 0,6% de carbono, 0,2% de neón, 0,15% de nitrógeno, 0,05% de magnesio, y, en menor porcentaje aún, hierro, sodio y silicio.
La composición química de una estrella varía según la generación a la que pertenezca. Cuánto más antigua sea, más baja será su metalicidad. Al inicio de su vida una estrella similar al Sol contiene aproximadamente 75% de hidrógeno y 23% de helio. El 2% restante lo forman elementos más pesados, aportados por estrellas que finalizaron su ciclo antes que ella. Estos porcentajes son en masa; en volumen, la relación es 90% de hidrógeno y 10% de helio.
En la Vía Láctea las estrellas se clasifican según su riqueza en metales en dos grandes grupos. Las que tienen una cierta abundancia se denominan de la población I, mientras que las estrellas pobres en metales forman parte de la población II. Normalmente la metalicidad está directamente relacionada con la edad de la estrella. A más elementos pesados, más joven es la estrella.

Un equipo japones de astrónomos han descubierto una fuerte correlación entre la metalicidad del disco de polvo protoplanetario y su longevidad. A partir de éste hallazgo proponen que las estrellas de baja metalicidad son menos propensas a tener planetas, incluyendo gigantes gaseosos, debido a la corta vida de los discos protoplanetarios.
La composición de una estrella evoluciona a lo largo de su ciclo, aumentando su contenido en elementos pesados en detrimento del hidrógeno, sobre todo. Sin embargo, las estrellas sólo queman un 10% de su masa inicial, por lo que globalmente su metalicidad no aumenta mucho. Además, las reacciones nucleares sólo se dan en las regiones centrales de la estrella. Este es el motivo por el que cuando se analiza el espectro de una estrella lo que se observa es, en la mayoría de los casos, la composición que tenía cuando se formó. En algunas estrellas poco masivas los movimientos de convección penetran mucho en el interior, llegando a mezclar material procesado con el original. Entonces se puede observar incluso en la superficie parte de ese material procesado. La estrella presenta, en esos casos, una composición superficial con más metales.

El tipo espectral estelar, conocido también como Clasificación espectral de Harvard, ya que lo comenzó a esbozar Edward Charles Picjering de la Universidad de Harvard en el año 1890, y que perfeccionó Annie Jump Cannon de la misma universidad en 1901, es la clasificación estelar más utilizada en astronomía. Las diferentes clases se enumeran de las más cálidas a frías. Son las siguientes:
| Clase | Temperatura | Color Convencional | Masa | Radio | Luminosidad | Líneas de absorción | Ejemplo |
|---|---|---|---|---|---|---|---|
| O | 28 000 – 50 000 K | Azul | 60 | 15 | 140 000 | Nitrógeno, carbono, helio y oxígeno | 48 Orionis |
| B | 9600 – 28 000 K | Blanco azulado | 18 | 7 | 20 000 | Helio, hidrógeno | Rigel |
| A | 7100 – 9600 K | Blanco | 3,1 | 2,1 | 80 | Hidrógeno | Sirio A |
| F | 5700 – 7100 K | Blanco amarillento | 1,7 | 1,3 | 6 | Metales: hierro, titanio, calcio, estroncio y magnesio | Canopus |
| G | 4600 – 5700 K | Amarillo | 1,1 | 1,1 | 1,2 | Calcio, helio, hidrógeno y metales | El Sol |
| K | 3200 – 4600 K | Amarillo anaranjado | 0,8 | 0,9 | 0,4 | Metales y óxido de titanio | Albireo A |
| M | 1700 – 3200 K | Rojo | 0,3 | 0,4 | 0,04 | Metales y óxido de titanio | Betelgeuse |
Las magnitudes Masa, Radio y Luminosidad, en proporción respecto al Sol (Sol=1).
La variedad de estrellas es grande y para los estudiosos fascinantes. Tal diversidad es debida a la evolución que desde su formación tiene cada tipo de estrella en función de su masa y de los gases y polvo cósmico que la forman y los que se crean en su núcleo (horno solar) a miles de millones de grados de temperatura capaces de transformar materiales simples como el hidrógeno hacia una gama más compleja y pesada que, finalmente, mediante la explosión de supernova (más temperatura), arroja al espacio materiales que, a su vez, forman nuevas estrellas de 2ª y 3ª generación con materiales complejos. La vida en nuestro planeta pudo surgir gracias a que en la Tierra había abundancia de estos materiales creados en las estrellas. Podemos decir, sin temor a equivocarnos que nosotros mismos estamos hechos del material creado en las estrellas lejanas que posiblemente, hace miles de millones de años explotó en supernova a millones de años luz de nuestro Sistema Solar.
Pero el Universo se rige por lo que llamamos las Fuerzas y Constantes Fundamentales de la Naturaleza, tenemos que decir que, precisamente, estas constantes son las que tienen el mérito de que las estrellas brillen en las galaxias y de que nosotros estemos aquí para mirar a los cielos y contemplar su belleza.
Las constantes fundamentales (constantes universales) están referidas a los parámetros que no cambian a lo largo del universo. La carga de un electrón, la velocidad de la luz en el espacio vacío, la constante de Planck, la constante gravitacional, la constante eléctrica y magnética se piensa que son todos ejemplos de constantes fundamentales.
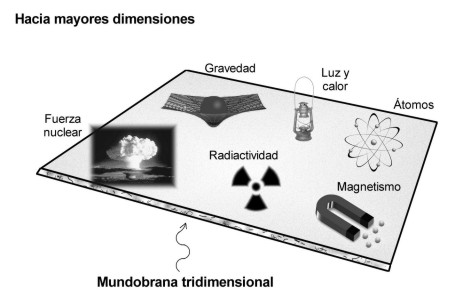
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil.
Las fuerzas fundamentales
|
Tipo de Fuerza |
Alcance en m |
Fuerza relativa |
Función |
| Nuclear fuerte |
<3×10-15 |
1041 |
Une Protones y Neutrones en el núcleo atómico por medio de Gluones. |
| Nuclear débil |
< 10-15 |
1028 |
Es responsable de la energía radiactiva producida de manera natural. Portadoras W y Z– |
| Electromagnetismo |
Infinito |
1039 |
Une los átomos para formar moléculas; propaga la luz y las ondas de radio y otras formas de energías eléctricas y magnéticas por medio de los fotones. |
| Gravitación |
Infinito |
1 |
Mantiene unidos los planetas del Sistema Solar, las estrellas en las galaxias y, nuestros pies pegados a la superficie de la Tierra. La |
El hipotético gravitón transporta la Gravedad pero está fuera del Modelo estándar
Las constantes fundamentales
|
Constante |
Símbolo |
Valor en unidades del SI |
| Aceleración en caída libre |
g |
9,80665 m s-2 |
| Carga del electrón |
e |
1,60217733(49) × 10-19 C |
| Constante de Avogadro |
NA |
6,0221367 (36) × 1023 mol-1 |
| Constante de Boltzmann |
K=R/NA |
1,380658 (12) × 10-23 J K-1 |
| Constante de Faraday |
F |
9,6485309 (29) × 104 C mol-1 |
| Constante de los gases |
R |
8,314510 (70) × J K-1 mol-1 |
| Constante de Loschmidt |
NL |
2,686763 (23) × 1025 mol-3 |
| Constante de Planck |
h |
6,6260755 (40) × 10-34 J s |
| Constante de Stefan-Boltzmann |
σ |
5,67051 (19) × 10-8 Wm-2 K-4 |
| Constante eléctrica |
ε0 |
8,854187817 × 10-12 F m-1 |
| Constante gravitacional |
G |
6,67259 (85) × 10-11 m3 Kg-1 s-2 |
| Constante magnética |
μ0 |
4π × 10-7 Hm-1 |
| Masa en reposo del electrón |
me |
9,1093897 (54) × 10-31 Kg |
| Masa en reposo del neutrón |
mn |
1,6749286 (10) × 10-27 Kg |
| Masa en reposo del protón |
mp |
1,6726231 (10) × 10-27 Kg |
| Velocidad de la luz |
c |
2,99792458× 108 m s-1 |
| Constante de estructura fina |
α |
2 π e2/h c |
Unas pueden ser más constantes naturales que otras, pero lo cierto es que, de momento, han servido como herramientas eficaces.
La última lección importante que aprendemos de la manera en que números puros como α (alfa) definen el mundo, es el verdadero significado de que los mundos sean diferentes. El número puro que llamamos constante de estructura fina, e indicamos con α, es como hemos dicho antes, una combinación de e, c y h (el electrón, la velocidad de la luz y la constante de Planck). Inicialmente, podríamos estar tentados a pensar que un mundo en el que la velocidad de la luz fuera más lenta sería un mundo diferente. Pero sería un error. Si e, h y c cambian de modo que los valores que tienen en unidades métricas (o cualesquiera otras) fueran diferentes cuando las buscamos en nuestras tablas de constantes físicas, pero el valor de α permaneciera igual; este nuevo mundo sería observacionalmente indistinguible de nuestro mundo. Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza.

Si pudiéramos coger una Gran Nave superlumínica y recorriéramos el espacio interestelar paseando por las distintas regiones del Universo, veríamos que, todo es igual en todas partes: Cúmulos y supercúmulos de Galaxias, Galaxias cuajadas de estrellas en cúmulos y sueltas con sus sistemas planetarios, púlsares de giros alucinantes, magnéteres creando inmensos capos electromagnéticos, agujeros negros que se tragan todo lo que traspasa el Horizonte de suscesos, Hermosas y brillantes Nebulosas de las que surgen las nuevas estrellas.
Está claro que pensar siquiera en que en nuestro universo, dependiendo de la región en la que nos encontremos, habrá distintos leyes físicas, sería pensar en un universo chapuza. Lo sensato es pensar como Einstein y creer que en cualquier parte del universo rigen las mismas leyes físicas, hasta que no se encuentre pruebas reales a favor de lo contrario, los científicos suponen con prudencia que, sea cual fueren las causas responsables de las pautas que llamamos “Leyes de la Naturaleza”, es mucho más inteligente adoptar la creencia de la igualdad física en cualquier parte de nuestro universo por muy remota que se encuentre; los elementos primordiales que lo formaron fueron siempre los mismos,
Cuando los físicos empezaron a apreciar el papel de las constantes en el dominio cuántico y explotar la nueva teoría de la gravedad de Einstein para describir el universo en conjunto, las circunstancias eran las adecuadas para que alguien tratara de casarlas.

Sí, el Universo podría ser considerado como la mayor Obra de Arte que, a su vez, es capaz de generar otras Obras de Artes que, en alguna ocasión, dan mucho que pensar, ya que, el surgir de la vida partierndo del simple hidrógeno que evoluciona en las estrellas del cielo…es ¡Increíble! pero, sin embargo, nada más cierto hay.
Así entró en escena Arthur Stanley Eddington: un extraordinario científico que había sido el primero en descubrir cómo se alimentaban las estrellas a partir de reacciones nucleares. También hizo importantes contribuciones a nuestra comprensión de las galaxias, escribió la primera exposición sistemática de la teoría de la relatividad general de Einstein y fue el responsable de la expedición que durante un eclipse de Sol, pudo confirmar con certeza la predicción de la relatividad general que debería desviar la luz estelar que venía hacia la Tierra en aproximadamente 1’75 segundos de arco cuando pasaba cerca de la superficie solar, cuyo espacio estaría curvado debido a la gravedad generada por la masa del Sol. En aquella expedición, el equipo de Eddington hizo una exitosa medición del fenómeno desde la isla Príncipe, que confirmó que Einstein tenía razón y que su teoría predecía de manera exacta la medida de curvatura del espacio en función de la masa del objeto estelar que genera la gravitación distorsionando el espaciotiempo a su alrededor.
El pasado año 2.015 fue el Año Internacional de la Luz, y, no debemos perder de vista que la luz tiene tanto importancia para vida como el agua. Sin luz tendríamos un planeta oscuro con un asola nochr eterno, frío de tenebroso, sin esos bellos rincones que se pueden conformar cuando la luz, encide en una montaña, en el bosque, en el horiozonte del Océano, o, simplemente sew refleja en la blanca nieve, en las olas del Mar o en una atronadora catarata.
La luz Natural es un don que nos dio la Natursleza y hace posibre que esa luz y ese calor que el Sol nos envia, haga posible la vida en el planrte, se produzca la tan necesario fotosíntesis, y muchos más beneficiosos fenónomemos que, no siempre sabemos valorar en su justa medida.
emilio silvera















 Totales: 85.691.174
Totales: 85.691.174 Conectados: 57
Conectados: 57

























