Feb
14
¿La Naturaleza? ¡Simetría dentro de la Diversidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Simetrías ~
Clasificado en Simetrías ~
 Comments (0)
Comments (0)

Nuestro mundo, aunque en la Galaxia existan muchos como él (que no los hemos podido encontrar), es un lugar privilegiado que conforma un Ecosistema superior en su conjunto formado por muchos ecosistemas locales aislados los unos de los otros y sin embargo, todos conexionados. La Diversidad de regiones diferentes que existen dentro del mismo planeta es asombrosa y, lo mismo nos podemos encontrar en un lugar como ese que vemos arriba, o en una isla paradisíaca, una selva, un desierto, o perdidos en un inmenso y embravecido océano, en la ventisca de nieve de inmensas montañas y, también, en grutas enormes en las profundidades del planeta.

Esos pequeños “seres” a los que llamamos extremófilos… los ambientes que habitan, estos poseen un ciclo reproductivo y un metabolismo muy lento; en los casos más extremos, solo se produce el proceso de división …
Pero todos esos climas diferentes son el resultado de la diversidad y, en cada uno de esos lugares ocurren cosas y, la vida, aunque parezca imposible, está allí presente. Es la consecuencia de que el planeta Tierra esté situado en la zona habitable del Sol, ni demasiado cerca para que la vida perezca achicharrada, ni demasiado lejos para que resulte congelada por el frío. Aquí el agua discurre líquida y cantarina por multitud de lugares y hace posible que, entre el preciado líquido y los rayos del Sol que nos envían la luz y el calor necesarios para la fotosíntesis y la vida… ¡Podamos estar aquí!
Todos sabemos que la materia en nuestro Universo adopta muchas formas distintas: Galaxias de estrellas y mundos que, en alguna ocasión, pueden incluso tener seres vivos y algunos han podido evolucionar hasta adquirir la consciencia. Sin embargo, no me quería referir a eso que es bien sabido por todos, sino que, trato de pararme un poco sobre una curiosa propiedad que la materia tiene en algunas ocasiones y que, la Naturaleza se empeña en repetir una y otra vez: ¡La Simetría!

Las Galaxias espirales, la redondez de los mundos, las estrellas del cielo, los árboles y las montañas, los ríos y los océanos, las especies animales (incluída la nuestra) que, se repiten una y otra vez y, en general, salvando particularidades, todas repiten un patrón de simetría.
Recuerdo aquí aquel pensamiento de Paul Valery en el que nos decía:
“El Universo está construído según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto.”

La Naturaleza está llena de simetrías
La simetría es una propiedad universal tanto en la vida corriente, como desde un punto de vista matemático desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común. Es siempre lo mismo dentro de una inmensa diversidad formada por grupos iguales.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más. Hay distintas maneras de expresarla: “Conjunto de invariancias de un sistema”, podría ser una de ellas. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas.

Aquí hay mucho más de lo que a asimple vista parece
Los físicos teóricos también se guían en sus investigaciones por motivaciones estéticas tanto como racionales. Poincaré escribió: “Para hacer ciencia, es necesario algo más que la pura lógica”. Él identificó ese elemento adicional como la intuición, que supone “el sentido de la belleza matemática”. Heisenberg hablaba de “la simplicidad y belleza de los esquemas matemáticos que la Naturaleza nos presenta”.

La simetría está presente por todas partes y, cada objeto, tiene la suya que siempre, está relacionada con la de otro de la misma especie. Hay simetrías que en física incluye todos los rasgos de un sistema físico que exhibe propiedades de la simetría – eso es, que bajo ciertas transformaciones, aspectos de esos sistemas son “incambiables”, de acuerdo a una observación particular. Una simetría de un sistema físico es un rasgo físico o matemático de un sistema que es preservado sobre cierto cambio.
En matemática, una transformación es un operador aplicado a una función tal que bajo esa transformación, ciertas operaciones sean simplificadas. En ejemplo, en la aritmética cuando se busca un algoritmo de números, el proceso de búsqueda es reducido a la suma de los algoritmos de cada factor.

Por ejemplo, veámos la invariancia de escala: En un recipiente con agua a punto de hervor, las burbujas de vapor, nucleadas en el fondo del recipiente, crecen, se liberan, y fluctúan hasta la superficie de donde se escapan para la atmósfera. A la temperatura de ebullición, el agua existe al mismo tiempo en dos fases distintas – líquido y gas – y a medida que las burbujas se forman las dos fases se separan en el espacio. Si cerramos el recipiente la temperatura de ebullición aumenta, como en una olla a presión. A medida que la presión aumenta, el sistema llega al punto crítico, donde las propiedades del líquido y del gas se vuelven idénticas. Por encima de esa temperatura, en el régimen supercrítico, dejan de existir dos fases distintas y existe apenas un fluido homogéneo.

Cerca del punto crítico, la materia fluctúa sin límites. Burbujas y gotas, unas tan pequeñas como unos cuantos átomos, otras tan grandes como el recipiente, aparecen y desaparecen, se unen y se separan. Exactamente en el punto crítico la escala de las mayores fluctuaciones divergen, pero el efecto de las fluctuaciones en escalas menores no es despreciable. La distribución de las fluctuaciones es invariable para transformaciones de escala.
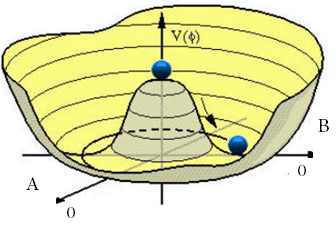
De la figura se deduce que la teoría tiene una “simetría interna”: la figura no cambia cuando hacemos rotaciones en el plano definido por A y B. La invariancia es definida matemáticamente por transformaciones que dejan magnitudes sin cambio. Por ejemplo, la distancia entre dos puntos de un sólido que se mueve, pero no se deforma.
Simetrías locales y globales


Una simetría global es una simetría que sostiene todos los puntos en el tiempo-espacio bajo consideración, a diferencia de la simetría local que solo sostiene a un subconjunto de puntos.
La mayoría de las teorías físicas son descritas por lagrangianos (En física, un lagrangiano es una función matemática a partir del cual se pueden derivar la evolución temporal, las leyes de conservación y otras propiedades importantes de un sistema físico) que son invariantes bajo ciertas transformaciones, cuando las transformaciones son realizadas en diferentes puntos del espacio-tiempo y están relacionadas linealmente – ellas tienen simetría global.
Por ejemplo, en toda teoría cuántica la fase global de una función de onda es arbitraria y no representa algo físico. Consecuentemente, la teoría es invariante bajo a cambio global de fases (Agregando una constante a la fase de todas las funciones de onda, en todos lados); esto es una simetría global. En la electrodinámica quántica, la teoría es también invariante bajo un cambio local de fase, es decir, que se puede alterar la fase de todas las funciones de onda tal que la alteración sea diferente en cada punto del espacio-tiempo. Esto es una simetría local.

También se habla de ruptura de simetrías temporales en la física de partículas.
Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una parte esencial de las leyes de la Naturaleza.
Se dice que esta ecuación de Euler es la más bella conocida. Aunque son muchas las ecuaciones que podríamos traer aquí y que son de todos conocidas y han quedado como símbolos en la historia de las matemáticas, la de Euler, es posible que por su elegancia y simplicidad, le pueda ganar a las demás en belleza. Ahí, en ese sencillo conjunto, los números más significativos de las matemáticas se abrazan: o, 1, e, π, y la unidad imaginaria i .
Si se fijan en la fórmula, en ella aparecen los 5 números más importantes en la historia de las matemáticas. El 0 y el 1 que, entre otras aportaciones a esta disciplina, son famosos por ser elementos neutros y, por lo tanto, indispensables en las operaciones de suma y producto; los números π y e, posiblemente, los dos irracionales más famosos (junto con φ, la razón aúrea) que existen (y que nos permiten hacer el chiste aquel de que la parte más irracional de nuestro cuerpo es el pi-e); y la unidad imaginaria, i, cuyo valor es
Dirac nos hablaba de ecuaciones bellas. La estética es, evidentemente, subjetiva, y la afirmación de que los físicos buscan la belleza en sus teorías tiene sentido sólo si podemos definir la belleza. Afortunadamente, esto se puede , en cierta medida, pues la estética científica está iluminada por el sol central de la simetría.

La Naturaleza nos la muestra por todas partes
La simetría es un concepto venerable y en modo alguno inescrutable y no podemos negar que tiene muchas implicaciones en la Ciencia, en las Artes y sobre todo, ¡en la Naturaleza! que de manera constante nos habla de ella. Miremos donde miremos…¡allí está!
El físico chino-norteamericano Chen Ning Yang ganó el Nóbel de Física por su en el desarrollo de una teoría de campos basada en la simetría y, aún afirmaba: “No comprendemos todavía el alcance del concepto de simetría”. Es lógico pensar que, si la Naturaleza emplea la simetría en sus obras, la razón debe estar implicada con la eficacia de los sistemas simétricos.
En griego, la palabra simetría significa “la misma medida” (syn significa “juntos”, como en sinfonía, una unión de sonidos, y metrón, “medición”); así su etimología nos informa que la simetría supone la repetición de una cantidad medible. Pero la simetría los griegos, también significaba la “la debida proporción”, lo que implicaba que la repetición involucrada debía ser armoniosa y placentera, como de hecho, resultan ser en las imágenes que arriba contemplamos. Asi, la Naturaleza nos está indicando que una relación simétrica debe ser juzgada por un criterio estético superior.

Humo simétrico
Muchos de nosotros, la mayoría, conocimos la simetría en sus manifestaciones geométricas de aquellas primeras clases en la Escuela Elemental, más tarde en el arte y, finalmente, la pudimos percibir en la Naturaleza, en el Universo y en nosotros mismos que, de alguna manera, somos de ese Universo de simetría.
Los planetas son esféricos y, por ejemplo, tienen simetría de rotación. Lo que quiere indicar es que poseen una característica -en caso, su perfil circular- que permanece invariante en la transformación producida cuando la Natuiraleza los hace rotar. Las esferas pueden Hacerse rotar en cualquier eje y en cualquier grado sin que cambie su perfil, lo cual hace que sea más simétrica.

La clave de la belleza está en la simetría
La simetría por rotación se encuentra en los pétalos de una flor o en los tentáculos de una medusa: aunque sus cuerpos roten, permanecen iguales. La simetría bilateral que hace que los lados derecho e izquierdo sean iguales y se presenta en casi todos los animales, incluido nosotros. Pero es uniendo estos aspectos se obtienen figuras realmente armoniosas. Si se trata de desplazamiento y rotación en un mismo plano hablamos de una espiral, mientras que en el espacio sería una hélice, aunque ambas se encuentran por todas partes en la naturaleza.
Las simetrías se generan mediante las fuerzas que actúan sobre los cuerpos, descritas por leyes rigurosas e inequívocas, como una fórmula matemática y dependen de la existencia de fuerzas distintas que actúan en diversas direcciones. Si éstas permanecen en equilibrio, no hay preferencia alguna hacia arriba o abajo, a la derecha o a la izquierda, y los cuerpos tenderán a ser perfectamente esféricos, como suele ocurrir en el caso de virus y bacterias, las estrellas y los mundos… las galaxias. Además, cuando el aspecto no es el de una esfera perfecta, la Naturaleza hará todo lo posible para hacercarse a esta.

La simetría también están prtesentes en nuestros cerebros
¿Sería posible que la simetría material tuviera un paralelismo en la abstracción intelectual que son las leyes físicas? luego hace falta un esfuerzo mental considerable para pasar de lo material a lo intelectual, pero cuando se profundiza en ellla, la conexión aparece. En la naturaleza existen muchas cosas que nos pueden llevar a pensar en lo complejo que puede llegar a resultar entender cosas que, a primera vista, parecían sencillas.
Me explico:

Fijémonos, por ejemplo, en una Flor de Girasol y en las matemáticas que sus semillas conllevan. Forman una serie de números en la que cifra es la suma de las dos precedentes (por ejemplo 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233…) se denomina, en términos matemáticos, sucesión de Fibonacci, una ley que se cumple incluso en el mundo vegetal, como hemos podido comprobar en las semillas del girasol, dispuestas en espiral y que respetan ésta fórmula. La podemos ver por todas partes.

Lo mismo ocurre con otros ejemplares de la diversidad del mundo de las plantas
En el mundo inorgánico las leyes de la cristalización del agua congelada, determinadas por las fuerzas que actúan entre las moléculas, hacen que los cristales adopten formas que son infinitas y varían con respecto a un tema común: la estrella de seis puntas. Sin embargo, los planetas son esféricos porque han nacido en la primordial que rodeaba al Sol, atrayendo materia indiferentemente de todas partes.

Claro que, en la Naturaleza, nada ocurre porque sí, todo tiene su por qué, y, todo lo que en ella podemos contemplar posee una funcionalidad que está directamente relacionada con su mecánica, con el medio en el que habita, con lo que el Universo espera que haga en su medio y, para ello, dota a figura con aquellos “trajes” que mejor les permita realizar aquello para lo que están destinados.
Vamos a generalizar un paso más el concepto de simetría, planteándonos si es posible que una ley física se cumpla en cualquier lugar. ¿En cualquier lugar… de dónde?, ¿de nuestra ciudad?, ¿de nuestro planeta? No: del universo. Una ley que fuera válida en cualquier lugar del universo sería una ley simétrica respecto al espacio. Se cumpliría dondequiera que se hiciese un experimento para comprobarla.
Fíjense que nuestra idea de simetría se va haciendo más compleja y más profunda. no nos detenemos en ver si la forma material de un objeto es simétrica, ni de si la escritura de una fórmula matemática es simétrica. Ahora nos preguntamos si una ley física es válida en todo el Universo.
La otra simetría interesante para una ley física es la que se refiere al tiempo. Cierta ley física se cumple ; ¿antes también?, ¿se cumplirá pasado algún tiempo? Una ley que fuera cierta en cualquier instante de la historia del universo sería una ley simétrica respecto al tiempo.

Lo que nos preguntamos es: ¿son simétricas o no las leyes de la física?
Hasta donde alcanzan nuestras medidas, las leyes físicas (y, por tanto, la interacción gravitatoria) sí son simétricas respecto al espacio y respecto al tiempo. En cualquier lugar y momento temporal del universo, la Naturaleza se comporta igual que aquí y ahora en lo que se refiere a estas leyes.
Esta simetría es un arma muy poderosa para investigar hacia el pasado y hacia el futuro, ya que nos permite suponer (y, en la medida en que confiemos en la seguridad de la simetría,conocer) locales donde jamás podremos llegar por la distancia espacial y temporal que nos separa de muchas partes del universo. Así, por ejemplo, gracias a esta simetría, podemos calcular que el Sol lleva 5.000 millones de años produciendo energía y que le quedan, probablemente, otros 5.000 millones hasta que consuma toda su masa. Esto lo podemos aventurar suponiendo que en ese enorme tramo de 5.000 + 5.000 = 10.000 millones de años las leyes físicas que determinan los procesos mediante los cuales el Sol consume su propia masa como combustible (las reacciones nucleares que le permiten producir energía), fueron, son y serán las mismas aquí en el Brazo de orión donde nos encontramos como en los arrabales de la Galaxia Andrómeda donde luce una estrella como nuestro Sol que, también envía luz y calor a sus planetas circundantes, y, por muy lejos que podamos mirar, siempre veremos lo mismo.

Por tanto, en cierto modo, la simetría se vuelve tan importante o más que la propia ley física.
La regularidad de las formas de la Naturaleza se refleja incluso en la cultura humana, que desde siempre intenta inspirarse en el mundo natural conformar su propio mundo. Existen hélices en las escaleras de palacios, castillos y minaretes y en las decoraciones de esculturas y columnas. Las espirales abundan en los vasos, en los bajorrelieves, en los cuadros, en las esculturas en los collares egipcios, griegos, celtas, precoolombinos e hindúes e, incluso, en los tatuajes con los que los maoríes neozelandeses se decoran el rostro.

¿Tenía en mente Leonardo la proporción áurea a la hora de realizar su obra maestra? Afirmarlo resultaría aventurado. Menos polémico es aseverar que el genio florentino concedía gran importancia a la relación entre la estética y la matemática. Dejaremos la cuestión en el aire por el momento, no sin antes mencionar que Leonardo realizó las ilustraciones de una obra de contenido estrictamente matemático, escrita por su buen amigo Luca Pacioli, llamada “De divina proportione”, es decir, “La divina proporción”.
Fuente de esta imagren y texto: Fernando Corbalán
La búsqueda de la perfección geométrica y de las propiedades matemáticas pueden ser una guía importante en el estudio científico del mundo. Paul Dirac, una de los padres de la moderna mecánica cuántica, solía decir que “si una teoría es bella desde el punto de vista matemático, muy probablemente es también verdadera”.

A todo esto, no debemos olvidar que todo, sin excepción, en nuestro Universo, está sometido a la Entropía que nos trae el paso inexorable de eso que llamamos “Tiempo”, y que, convierte perfectas simetrias de joven belleza, en deteriorados objetos o entidades que, nos viene a recordar que nada es perpetuo, que todo pasa y se transforma. Claro que, de alguna manera, todo vuelve a resurgir.

La belleza que atrae, rara vez coincide con la belleza que enamora
Un dolor que llevo dentro de mí es el no poder contemplar la verdadera belleza que estándo presente en los seres vivos inteligentes, en la mayoría de los casos, se nos queda oculta a nuestra percepción, toda vez que esa clase de belleza, que no podemos ver pero sí percibir, sólo la podemos captar con el trato y la convivencia y, verdaderamente, tengo que admitir que, algunas bellezas que he tenido la suerte de poder “ver con los ojos del espíritu”, llegan a ser segadoras, deslumbrantes, su explendor es muy superior al de la estrella más brillante del cielo, y, seguramente (estoy seguro) como a muchos de ustedes les pasa, tengo la suerte de tenerla junto a mí desde hace muchos años. y, si pienso en ello en profundidad y detenimiento, no tengo más tremedio que concluir que es ese brillo y esplendor el que me da la fuerza para seguir cada dia en la dura lucha que nos ha participar.
¡Sí que es importante la Belleza! Dirac tenía toda la razón. Y, no digamos las Simetrías que indican con el dedo de la Naturaleza el camino a seguir a muchos físicos que quieren desvelar sus secretos.
emilio silvera
Feb
14
Cúmulo abierto M67
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astrofísica ~
Clasificado en Astrofísica ~
 Comments (0)
Comments (0)


Planetas mayores que Júpiter orbitan algunas de sus estrellas
M67 (también conocido como NGC 2682) es un cúmulo abierto situado en la constelación de Cáncer.
M67 tiene aproximadamente 500 componentes. Contiene 11 estrellas gigantes de tipo espectral K con magnitud absoluta entre +0.5 y +1.5, así como algunas estrellas en la zona más azul de la Secuencia Principal, la más brillante de ellas de tipo espectral B8 o B9. También posee 200 enanas blancas (esto quiere decir que doscientos soles murieron para que ellas existieran) y 100 estrellas parecidas a nuestro sol. La magnitud aparente de sus estrellas más brillantes es alrededor de 10ª.

Debido al alto número de estrellas, de tipos tan distintos, ha sido estudiado intensamente: Harlow Shapley (1917) realizó los primeros trabajos sobre sus colores y magnitudes, Barnard (1931) midió la posición de sus principales componentes (para determinar sus movimientos propios), Popper (1954) los espectros de sus brillantes estrellas, mientras que Johnson y Sandage (1955) elaboraron el primer Diagrama HR preciso de alrededor de 500 estrellas, descubriendo su elevada edad y su estado tan evolucionado.

Estas binarias se pueden fusionar para formar una estrella de Neutrones
Hasta la fecha (2.016) se han descubierto la presencia de 45 fuentes de Rayos X en el cúmulo, la mayoría de ellas estrellas binarias ellas (presumiblemente del tipo RS CVn), con períodos orbitales de 10 días o menos.
En su parte sur, prácticamente en la zona occidental, aparece un pequeño agrupamiento de nueve estrellitas conocido como Dipper: tiene forma de pequeña cometa con la cola curvada; una de sus estrellas componentes es la variable S 999.




Contiene bastantes variables del tipo binaria eclipsante y binaria espectroscópica; algunas de estas estrellas, fácilmente visibles para telescopios de aficionado dotado de cámara CCD son:
- AH Cnc: de magnitud 13.33, es una binaria del tipo UW UMa descubierta en 1960; su período es igual a 0.360452 días, su amplitudes próxima a 0.40 magnitudes.
- EV Cnc: de magnitud 12.78, también es una binaria de tipo UW UMa; fue descubierta en 1991, tiene un período igual a 0.44144 días y una amplitud igual a 0.18 magnitudes.
- AG Cnc: con magnitud 13.77 presenta un período igual a 2.84 días y una amplitud de 0.20 magnitudes.
- S 999: de magnitud 12.60 es una variable de largo período (9.2 días) que presenta una amplitud fotométrica igual a 0.07 magnitudes; está situada en la parte norte del Dipper.
- S 1063: también conocida como NSV 4274, es un astro de magnitud 13.79 con un período de variación muy largo, comprendido entre los 17 y 18 días (hasta el año 2006 no está bien determinado), con una amplitud de 0.18 magnitudes.
- ES Cnc: con magnitud 11.19 es una de las más brillantes del cúmulo; se trata de una estrella del tipo blue straggler (errante azul) que resulta ser también una variable eclipsante con un período igual a 1.0677978 días.
En 2004 se publicó un estudio del cúmulo en el que se midieron las magnitudes de sus estrellas con una precisión de diezmilésimas de magnitud: (0.0001 magnitud).
Fuente de datos de Wikipedia.
Feb
14
Moléculas Quirales y otras maravillas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo y la Química de la Vida ~
Clasificado en El Universo y la Química de la Vida ~
 Comments (0)
Comments (0)
Artículo publicado por Lori Dajose el 14 de junio de 2016 en Caltech News
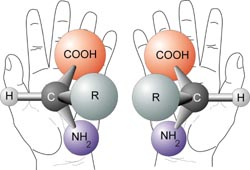
Las moléculas quirales – compuestos que aparecen en variaciones que son imágenes especulares unas de otras, como un par de manos humanas — son cruciales para la vida tal como la conocemos. Los seres vivos son selectivos sobre qué tipo de “orientación” de una molécula usan o producen. Por ejemplo, todos los seres vivos usan exclusivamente la forma dextrógira de la ribosa (el armazón del ADN), y las uvas exclusivamente sintetizan la forma levógira de la molécula del ácido tartárico. Aunque la homoquiralidad — el uso de sólo una orientación de una molécula dada — es ventajoso evolutivamente hablando, no se sabe cómo elige la vida la orientación molecular que vemos en la biosfera.
Así comenzó el artículo publicado en Caltech News.
Lo podemos continuar con otros datos e ingredientes que nos llevan a saber, cómo se vale la naturaleza de su “magía” para conseguir lo que quiere. Todo esto es bastante complejo y podemos hallar en Nubes Moleculares algunas moléculas que son esenciales para la vida, así que, podríamos decir que muchos de los ingredientes de los que están hechos los seres vivos se hicieron y formaron en el Espacio Interestelar.

La catálisis asimétrica hace referencia a la catálisis efectuada por catalizadores quirales que además de acelerar una reacción, inducen la formación preferente de uno o varios estereoisómeros de todos los posibles. Este proceso implica una “multiplicación” de la quiralidad y es, por tanto, el método ideal para la síntesis de compuestos ópticamente puros.
En función de la naturaleza metálica o no metálica del catalizador, la catálisis asimétrica puede dividirse en catálisis organometálica (utiliza como especies catalíticas complejos metal-ligando orgánico quiral) y organocatálisis (utiliza como especies catalíticas moléculas orgánicas pequeñas, de bajo peso molecular).
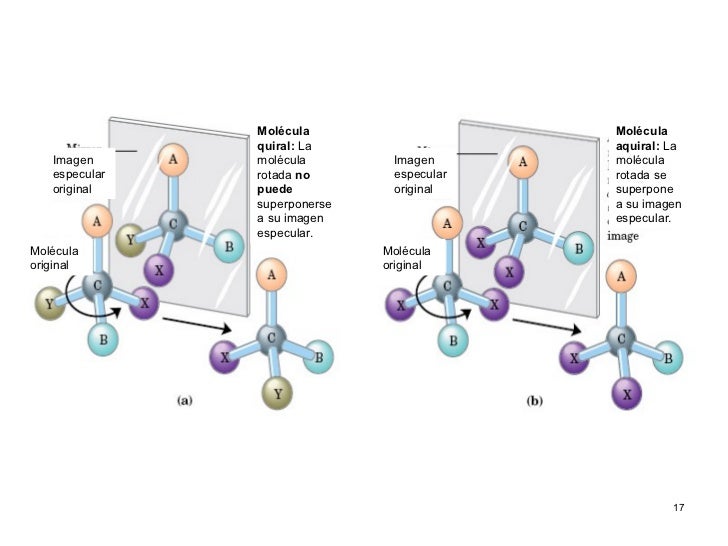
ISÓMEROS (Compuestos con la misma fórmula molecular, pero presentan diferentes propiedades químicas debido a que su estructura es distinta) ISOMERÍA ESTRUCTURAL (Presentan diferente estructura debido a que presentan distintos tipos de enlaces en la cadena o en la unión entre átomos) ISOMERÍA ESPACIAL ESTEREOISOMERÍA (Presentan diferente orientación espacial de algunos de sus átomos) Isomería de cadena (Forman cadenas carbonadas distintas) Isomería de posición (La localización de las ramificaciones, insaturaciones o grupos funcionles son distintas) Isomería de función (Tienen grupos funcionales distintos) Isomería geométrica Diastereoisomería (Se debe a las posibles orientaciones cuando los átomos de carbono están unidos por enlaces que no pueden rotar) Isomería óptica Enantiomería (Se debe a las posibles orientaciones cuando los átomos de carbono están unidos por enlaces que no pueden rotar).
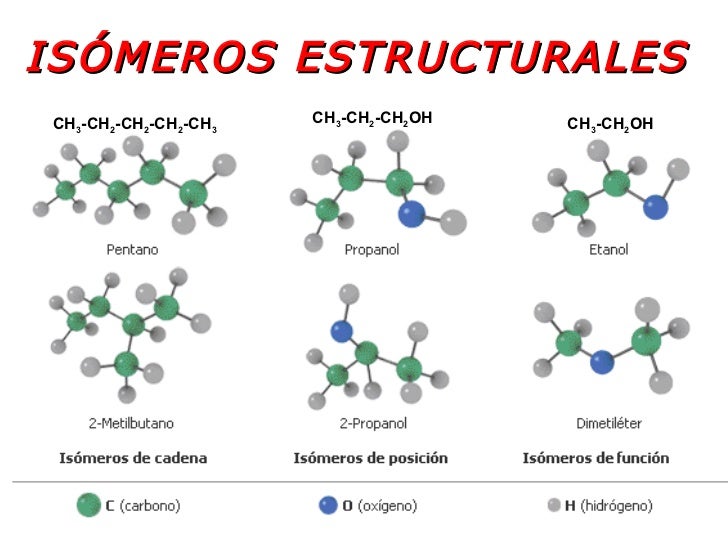
ISÓMEROS ESTRUCTURALES
ISÓMEROS DE CADENA
ISÓMEROS DE POSICIÓN
ESTEREOISÓMEROS L
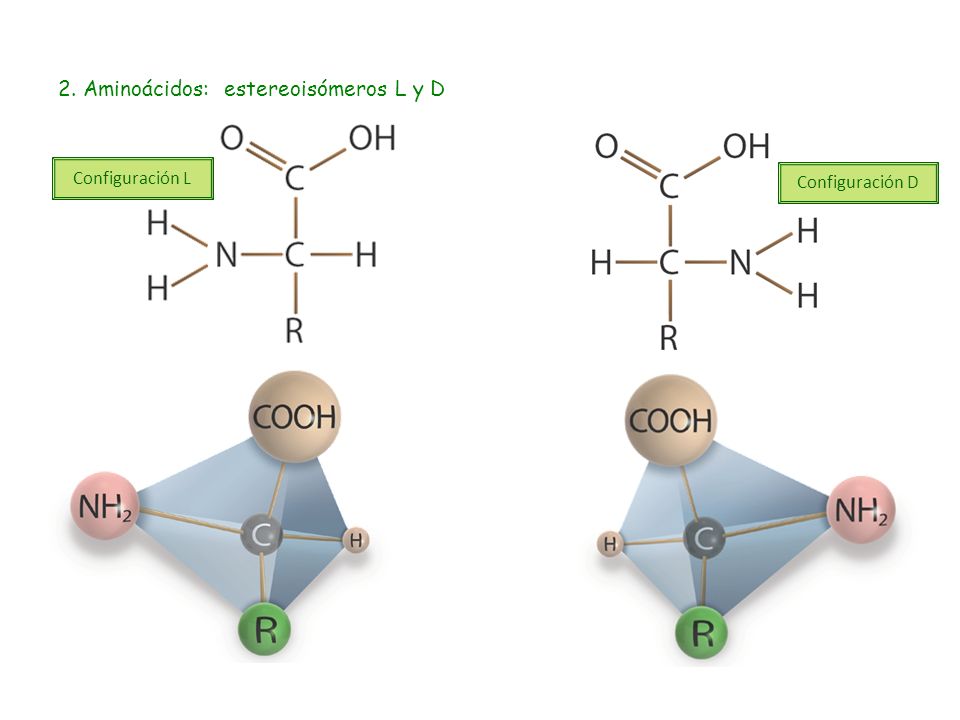
Cada una de estas modalidades y otras que se conocen tiene un cometido distinto pero, al final del camino, se ellas se vale la Naturaleza para alcanzar sus logros
Un grupo de investigadores internacionales estudian la forma en que se podría desarrollar en el espacio un tipo particular de moléculas orgánicas en una nebulosa, las cuales son materia prima para la vida.
Las moléculas llevan por nombre Hidrocarburo Aromático Policíclico (PAHs, por sus siglas en inglés), y se tratan de elementos planos que constan de átomos de carbono dispuestos en un patrón de panal, rodeadas de hidrógeno.
Dicha información ayudaría a los científicos a comprender mejor la manera en que se pudo generar la vida en la Tierra, informó en su página de Internet, la Administración Nacional de Aeronáutica y del Espacio (NASA, por sus siglas en inglés).
De acuerdo con la agencia estadounidense, los PAHs representan 10 por ciento del carbono en el universo, los cuales se pueden encontrar en la Tierra al momento de la combustión de material orgánico, como la carne, la caña de azúcar y la madera, entre otros.

Como todos saben, en las Nebulosas están presentes muchas moléculas necesarias para la vida. En comentarios anteriores, ya nos referimos a los elementos más idóneos para formarlas y, cuando en esas Nebulosas el material allí presente se transforma en Mundos, allí aparecen y se juntan para evolucionar y conseguir maravillas que, como la Vida, nos llevan al Asombro.

Lo cierto es que no podemos contestar algunas pregunta con propiedad. Sabemos lo que son los seres vivos e incluso, es posible que existan algunas especies que estando vivas ni lo podamos saber ni las podemos detectar. Sabemos de los materiales que son necesarios para que la vida esté presente en nuestro Universo y, en éstas mismas páginas hemos expuestos amplios trabajos sobre el tema de la vida, su posible origen, de cómo se “fabrican” los materiales necesarios para su existencia en las estrellas… Se podría decir, sin andar muy lejos de la verdad, que la vida, es la materia evolucionada hasta el nivel de la consciencia (si nos referimos ala vida en su más alta expresión).
Pero llegar más lejos… ¡No podemos! de momento.
Artículo híbrido rematado por emilio silvera.
















 Totales: 75.502.778
Totales: 75.502.778 Conectados: 35
Conectados: 35























