La inducción probabilística:

• Todo estudio científico se compone de fases de observación, procesamiento y conclusiones finales (o leyes generalistas). Una observación puntual puede arrojar resultados que no sean los esperados por lo que en muchos casos se hace uso de la probabilidad.

“El nacimiento y desarrollo de la ciencia experimental a partir del siglo XVII ha estado frecuentemente acompañado de polémicas filosóficas, y no pocas posturas filosóficas de la época moderna han representado, en parte, intentos diversos de solucionar esas polémicas”.

Resolver las diferentes polémicas filosóficas han hecho que en la época reciente se constituyese “la filosofía de la ciencia como disciplina autónoma, que ha dado lugar a la aparición de un nuevo tipo de dedicación profesional”.

 

 

      Karl Popper

La aparición de este nuevo tipo de filósofo suele estar ligada a las actividades del círculo de Viena “que contribuyeron decisivamente a la consolidación de la filosofía de la ciencia como disciplina autónoma”. Desde esas actividades surgieron nuevas figuras que, ancladas en las consideraciones iniciales de la filosofía neopositivista del Círculo intenta responder a la cuestión de qué es la actividad científica y cual es su racionalidad propia. Heredan de la visión positivista que la ciencia es el paradigma de la objetividad y de la racionalidad.

Junto a la postura neopositivista crecen las figuras de otros pensadores. Entre esos nuevos filósofos se encuentra Karl Popper, cuya filosofía es también un intento de explicar el método científico y la racionalidad propia de la ciencia. Se convierte, tras alguno de los miembros del Círculo, en uno de los principales artífices de la consolidación de esta disciplina. A su sombra crecieron los principales filósofos de la ciencia del siglo XX y sus ideas constituyen siempre un paradigma, ya sea para seguirlas, ya sea para criticarlas.

Aquí yace en Paz el cuerpo de Karl Popper, ya que sus pensamientos vagan por todo el Universo… ¡libres! Los logros filosóficos de Karl Popper le valieron numerosos reconocimientos, tales como ser nombrado caballero por la reina Isabel II del Reino Unido en 1969. Recibió la insignia de Compañero de Honor (Companion of Honour) en 1982, el premio Lippincott de la Asociación Norteamericana de Ciencias Políticas y el premio Sonning. Fue miembro de la Sociedad Mont Pelerin, una comunidad de estudios fundada por Hayek para promover una agenda política liberal, así como de la Royal Society de Londres,  con el rango de miembro, y de la Academia Internacional de la Ciencia.  Entre otras, cultivó la amistad del canciller alemán Helmut Schmidt.  Algunos conocidos discípulos de Popper fueron Hans Albert, Imre Lakatos y Paul Feyerabend.

“Creo, sin embargo, que al menos existe un problema filosófico por el que se interesan todos los hombres que reflexionan: es el de la cosmología, el problema de entender el mundo… incluidos nosotros y nuestro conocimiento como parte de él. Creo que toda ciencia es cosmología, y, en mi caso, el único interés de la filosofía, no menos que el de la ciencia, reside en los aportes que ha hecho a aquella; en todo caso, tanto la filosofía como la ciencia perderían todo su atractivo para mí si abandonasen tal empresa.”

 

Karl Popper. La lógica de la investigación científica. México, Rei, 1991.

No son pocos los filósofos que, con sus ideas, con su manera de ver el mundo, nos ayudaron a comprender, y, Karl Popper, fue uno de ellos-

• El problema principal: LOS LÍMITES Entre la ciencia y la metafísica Usando un criterio de ¿Cómo distinguir de los demarcación para que es ciencia de lo separar la ciencia de la que no lo es? especulación y la metafísica Para Popper una proposición es científica si puede ser refutable-
• Popper planteó que muchas proposiciones que para los pensadores de su época tenían significado, no podían calificarsecomo ciencia como, por ejemplo, el psicoanálisis o el marxismo y,obviamente, la religión, ya que ante cualquier crítica se defendían con hipótesis ad hoc que impedían cualquier refutación.
• En el sistema de Popper se combina la racionalidad con la extrema importancia que la crítica tiene en el desarrollo de nuestro conocimiento. Por eso, tal sistema fue bautizado como racionalismo crítico.

• FALSABILIDAD O FALSACIÓN.

Popper estaba de acuerdo con Hume respecto de que justificar nuestro conocimiento en forma inductiva conduce al irracionalismo. Pero, negaba que los científicos normalmente utilicen inferencias inductivas. A su vez, estaba de acuerdo con Kant acerca de que la experiencia y la observación presuponen ideas a priori. Pero, negaba que esas ideas a priori sean necesariamente verdaderas. Finalmente, estaba de acuerdo con Wittgenstein y los positivistas en que no podemos recurrir a principios válidos a priori para justificar la ciencia empírica. Pero, consideraba que la metafísica no tenía porqué carecer de sentido y que la verificabilidad es incapaz de distinguir a la ciencia de la metafísica puesto que no puede dar cuentas de la cientificidad de las leyes científicas, las cuales no pueden ser verificadas a través de argumentos inductivos derivados de la experiencia.

Aquí, Popper cortó el nudo gordiano al sugerir que las teorías científicas, en última instancia, no pueden ser justificadas. También al afirmar que el conocimiento científico es racional, no porque lo hayamos justificado, sino porque podemos criticarlo.

Para Popper, cualquier intento por justificar nuestro conocimiento debe aceptar algún enunciado como verdadero sin justificación alguna, a fin de evitar el regreso infinito.

Wittgenstein y los positivistas habían apelado a la experiencia para justificar nuestro conocimiento. Al contrario, Popper afirmó que ‘el principal problema de la filosofía es el análisis crítico del recurso a la autoridad de la ‘experiencia’ –precisamente la ‘experiencia’ que todo partidario del positivismo ingenuamente da por sentada’.

Popper creía que los enunciados observacionales jamás pueden suponer la veracidad de una ley universal. Además, Popper afirmó que sólo basta un contra-ejemplo para mostrar que una ley universal es falsa. Así, concluyó que es la falsabilidad lo que distingue a la ciencia de la metafísica. También postuló que la asimetría lógica entre los enunciados universales y singulares –las teorías científicas pueden ser falsadas, mas no verificadas; los enunciados observacionales pueden ser verificados, aunque no falsados– significa que la distinción entre ciencias naturales y metafísica no puede coincidir con la distinción entre enunciados con sentido y carentes de él.

Nuestro filósofo también negó que las teorías científicas sean descubiertas a través de un proceso inductivo. Popper pensaba que los científicos no desarrollan sus teorías generalizando observaciones, sino que inventan dichas teorías a modo de soluciones hipotéticas para los problemas con los que se enfrentan; y que deben recurrir a la experiencia y a las observaciones –no para justificar– sino para testear sus hipótesis. Por tanto, el crecimiento de la ciencia es tanto empírico como racional. Es empírico porque podemos testear nuestras hipótesis frente a observaciones y a la experiencia. Es racional puesto que utilizamos las formas válidas de argumentos de la lógica deductiva para criticar las hipótesis que contradicen enunciados observacionales que pensamos son verdaderos, y porque nunca arribamos a la conclusión de haber demostrado que una teoría es verdadera cuando la misma ha sobrevivido a nuestros tests.

Lo cierto es que no podemos plasmar aquí, en un corto espacio y limitado tiempo, los pensamientos de toda una vida y, nos limitamos a tomar datos de aquí y de allá para dejar un bosquejoque nos hable de quién fue el personaje y sus pensamientos.

La cortedad de miras es patente ¿qué irán buscando?

El no creía en los nacionalismos, decía que era como regresar a la Tribu.

¡Cuánta razóntenía! Un buen ejemplo lo tenemos cerca.

Por todo el mundo, en muchas de sus regiones, podemos ver los efectos negativos que dicho nacionalismo, por una u otra razón, la excusa no importea, los “inteligentes humanos” se matan. Y, de vez en cuando, sería bueno que algunos se pararan a pensar en los hechos y actuar después, emplear la lógica es bueno y debemos demostrar que somos seres raciponales. La Filosofía es un buen camino.

emilio silvera

[?]

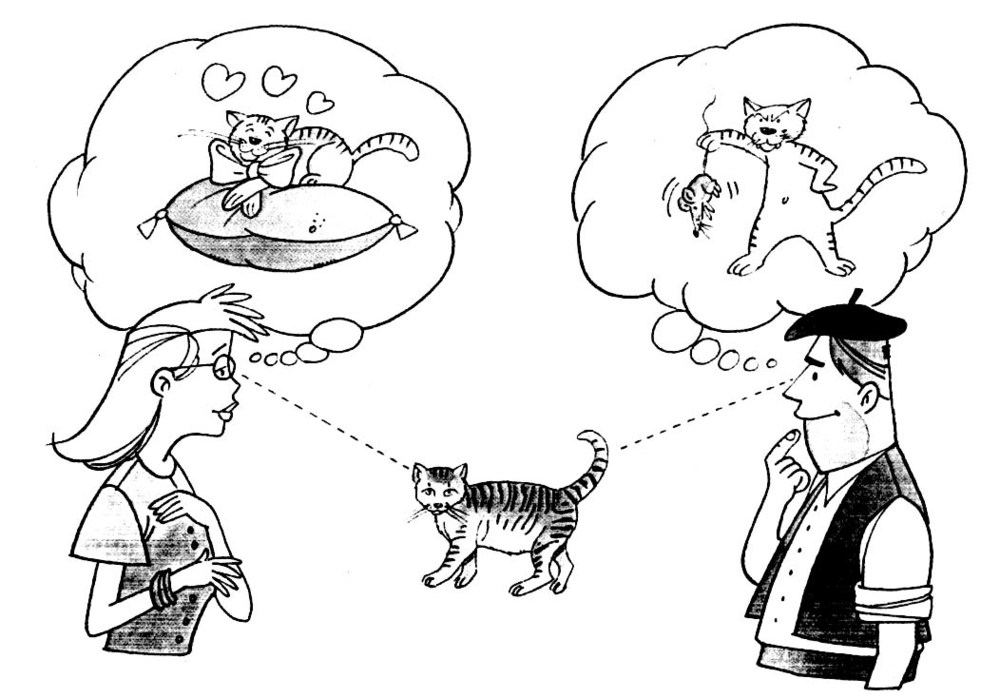
                 No todos vemos el mundo de la misma manera

Nuestra realidad es la que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”     Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.

Lo cierto es que, la única realidad vendrá de los descubrimientos que son desvelados y nos muestran los secretos d ela Naturaleza.

 

Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, para ello, encontramos las maneras de aproximarnos a esa realidad “presentida”.

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.

Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas  y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.

          En esta aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado.

Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:

1 – 1/3 + 1/5 – 1/7 ….

Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente,  se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que  independientemente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y  entre otros temas. Si hablamos de Pi mos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN  el Efecto mariposa y la Torah, entre otras muchísimas cosas que  se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes reopresentado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.

No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la Teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa” “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.

El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.

Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.

Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.

¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.

3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th

Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejmplo:

Roger Penrose dedicó bastante más tinta en defender  los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.

Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

                     ¿Es la verdad inalcanzable?

Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.

Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos  y dispares pensamientos:

• Los Computadores nunca podrán reemplazar la estupidez humana.
• El hombre nace ignorante,  la educación lo idiotiza.
• Una persona inteligente resuelve problemas, el genio los evita.
• Las mujeres consideran que guardar un secreto, es no revelar la fuente.
• Todas las mujeres tienen algo bonito… así sea una prima lejana.
• La felicidad es una lata de atún, pero con el abrelatas un poco distante.
• El único animal que no resiste aplausos es el mosquito.
• El amor está en el cerebro, no en el corazón.
• Definición de nostalgia “es la alegría de estar triste”.
• “Mi segundo órgano favorito es el cerebro”.

Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!

Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?

     Todo eso está bien pero, ¿Qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene el mismo área que el circulo”.

[?]

Descubren como afecta al cerebro tu canción favorita.

 Un estudio revela los efectos en el cerebro de nuestras melodías preferidas. Los resultados se han publicado en Sciencitific Reports, una de las Revistas de editorial Nature.

Los primeros acordes de nuestra canción favorita desencadenan un patrón común de actividad cerebral -se generan pensamientos y recuerdos­- independientemente de la persona que disfrute de la melodía. Sin embargo, hasta ahora no se conocía cómo se produce dicha activación en el cerebro. Los hallazgos, publicados este jueves en Scientific Reports, una de las revistas de la editorial Nature, podrían explicar por qué diferentes personas describen sentimientos y recuerdos similares al escuchar su pieza musical favorita, tanto si es una composición de Beethoven o Eminem.

Para entender por qué la gente tiene experiencias comparables, el grupo de investigación estadounidense evaluó las diferencias en las redes funcionales del cerebro (utilizando imágenes de resonancia magnética funcional, fMRI) en 21 personas que escucharon diferentes tipos de música, incluyendo rock, rap, y melodías clásicas. Los científicos identificaron modelos consistentes de la conectividad cerebral asociada a las canciones favoritas y demostraron que un circuito importante en los pensamientos introspectivos -la red neuronal por defecto (Default Mode Network o DMN, en inglés)- se conecta más cuando se escucha la música preferida.

Como explica a Sinc Jonathan Burdette, profesor del Centro Médico Wake Forest Baptist (EE UU) y uno de los principales autores del estudio, “aunque no entendemos completamente lo que hace la DMN, es probable que tenga un papel importante en la determinación de quiénes somos y cómo encajamos en el mundo”. Los expertos se refieren a esto como pensamientos autoreferenciales. Según los autores, los resultados fueron inesperados “dado que las preferencias musicales son fenómenos individualizados y que la música puede variar mucho en complejidad rítmica, presencia o ausencia de la letra, consistencia, etc.”.

    Canciones favoritas, viejas emociones

El trabajo pone de manifiesto que la escucha de una canción favorita altera la conectividad entre las áreas cerebrales auditivas y el hipocampo, una región responsable de la memoria y la consolidación de las emociones. Los expertos comprobaron así que al oír las melodías favoritas se produce una desconexión de las áreas de procesamiento de sonido del cerebro en las zonas de codificación de la memoria de dicho órgano. “Esto se debe probablemente a que al escuchar nuestra música favorita, no estamos creando nuevos recuerdos. Más bien, estamos aprovechando recuerdos y viejas emociones”, subraya Burdette.

Para los autores, estos hallazgos podrían tener importantes implicaciones en la terapia musical, sobre todo en la elección apropiada de la música capaz de involucrar a los circuitos cerebrales dañados.

Fuente:Público.es

Escuchar una canción alegre puede subir nuestro animo , si oímos un tema deprimente, sentirnos pesimistas o, en el caso de una melodía suave, relajarnos y afrontar mejor el momento.

No hay duda de que la música afecta nuestro estado anímico y provoca una serie de sensaciones, pero ¿Sabes cómo afecta la música a nuestro cerebro? Un estudio de la Universidad de Florida, lo reveló.

Cómo la música afecta nuestro cerebro

[?]

Leo Rojas llegó en 2000 desde su casa en España, mientras su familia permanecía en Ecuador. De allí se trasladó con una visa de turista otra vez a Alemania. Vive con su esposa polaca en Berlín, donde obtuvo dinero como músico callejero. Un transeúnte llamó su atención para que ingrese al programa de talentos Das Supertalent. Ingresó a la quinta temporada en 2011 y clasificó para la fase final. Con una interpretación de El cóndor pasa con zampoñas y otros instrumentos de viento de América del Sur, llegó a las semifinales. Allí se reunió con su madre que fue trasladada desde Ecuador, en un reencuentro emocional. En la final, el 17 de diciembre de 2011, Rojas tocó el tema instrumental Einsamer Hirte, un éxito escrito por James Last en 1977 para Gheorghe Zamfir. Con una clara ventaja el sudamericano ganó la competencia.

Veamos la actuación de Leo que, metiendose en el ambiente, se pone los pelos de punta.

Leo Rojas – El Condor Pasa

Que lo disfruteis.

[?]