Ago
27
Teorías, masas, partículas, dimensiones…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)


Las Teorías:
Una nos habla del Cosmos y de como el espacio se curva ante la presencia de masas, la otra, nos habla de funciones de ondas, entrelazamientos cuánticos, de diminutos objetos que conforman la materia y hacen posibles los átomos y la vida.
Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.
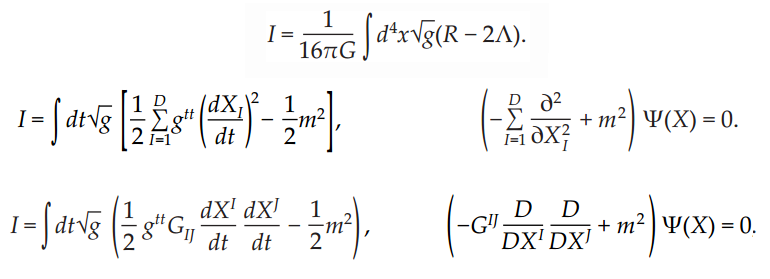
Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
La longitud de Planck (ℓP) u hodón (término acuñado en 1926 por Robert Lévi) es la distancia o escala de longitud por debajo de la cual se espera que el espacio deje de tener una geometría clásica. Una medida inferior previsiblemente no puede ser tratada adecuadamente en los modelos de física actuales debido a la aparición de efectos de Gravedad Cuántica.
Equivale a la distancia que recorre un fotón, viajando a la velocidad de la luz, en el tiempo de Planck.
¿Quién puede ir a la longitud de Planck para verla? A distancias comparables con la longitud de Planck, se cree que están sucediendo cosas muy curiosas que rebasan ampliamente los límites de nuestra imaginación. A diferencia de la filosofía reduccionista que propone que lo más complejo está elaborado -axiomáticamente- a partir de lo más elemental, lo que está sucediendo en la escala de Planck no parece tener nada de elemental o sencillo. Se cree que a esta escala la continuidad del espacio-tiempo en vez de ir marchando sincronizadamente al parejo con lo que vemos en el macrocosmos de hecho stá variando a grado tal que a nivel ultra-microscópico el tiempo no sólo avanza o se detiene aleatoriamente sino inclusive marcha hacia atrás, una especie de verdadera máquina del tiempo. Las limitaciones de nuestros conocimientos sobre las rarezas que puedan estar ocurriendo en esta escala en el orden de los 10-35 metros, la longitud de Planck, ha llevado a la proposición de modelos tan imaginativos y tan exóticos como la teoría de la espuma cuántica que supuestamente veríamos aún en la ausencia de materia-energía si fuésemos ampliando sucesivamente una porción del espacio-tiempo plano.

La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.

Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que mencioné en páginas anteriores.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.
¡Necesitamos algo más avanzado!
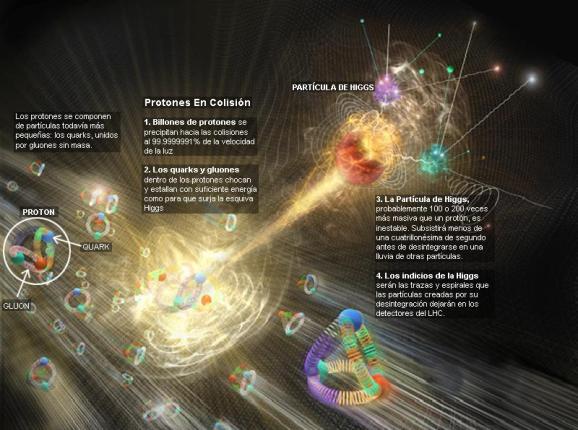
Cada partícula tiene encomendada una misión
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las demás partículas. Cuando su autor lanzó la idea al mundo, resultó además de nueva muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.
Cuando los físicos hablan de la belleza de algunas ecuaciones, se refieren a las que, como ésta, dicen mucho con muy pocos caracteres. De hecho, puede que ésta sea la ecuación más famosa conocida en nuestro mundo.
Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
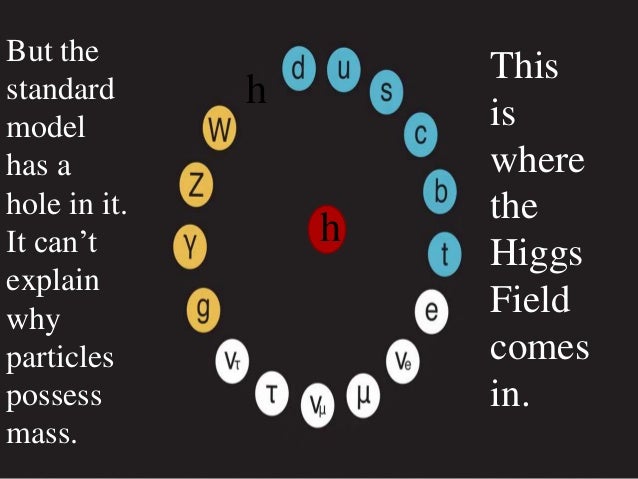
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta hace bien poco no teniamos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC cuando la buscaba). Pero el problema es irritante: ¿por qué sólo esas masas -Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa -los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébilse fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
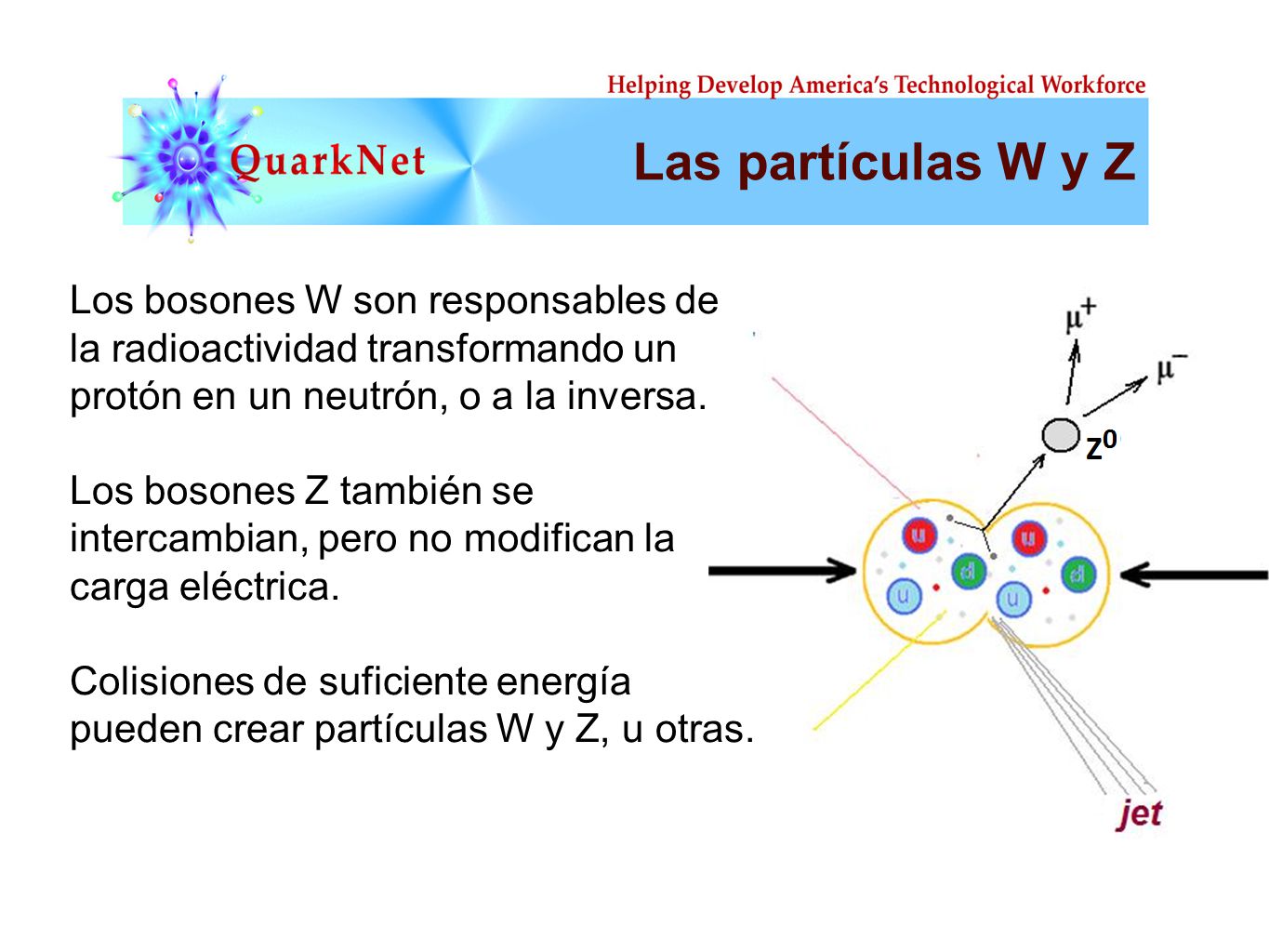
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.
Pero, encierra tantos misterios la materia que, a veces me hace pensar en que la podríamos denominar de cualuquier manera menos de inerte ¡Parece que la materia está viva!
Son muchas las cosas que desconocemos y, nuestra curiosidad nos empuja continuamente a buscar esas respuestas.

El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).
Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto. Conocemos su masa y su carga negativa que responden a 9,1093897 (54) x 10-31 Kg la primera y, 1,602 177 33 (49) x 10-19 culombios, la segunda, y también su radio clásico: r0 = e2/mc2 = 2’82 x 10-13 m. No se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.
Lo cierto es que, el electrón, es una maravilla en sí mismo. El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

¡No por pequeño, se es insignificante!
Recordémoslo, todo lo grande está hecho de cosas pequeñas.
En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo). Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones*.
Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

El fotón tiene una masa de 1, una carga eléctrica de o, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos: Ve, Vu y VT.
Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales. Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.

La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.

Han llevado años captarlas, las ondas gravitatorias llevadas por el gravitón son débiles
Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.
De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es o, su carga es o, y su espín de 2. Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.

Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros. Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.
La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.
Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo. Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.

Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e ineliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.
Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita. En un bajo vacío, la presión se reduce hasta 10-2 pascales, mientras que un alto vacío tiene una presión de 10-2-10-7 pascales. Por debajo de 10-7 pascales se conoce como un vacío ultraalto.
No puedo dejar de referirme al vaciotheta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs).

El vacío theta es el punto de partida para comprender el estado de vacío de las teoría gauge fuertemente interaccionantes, como la cromodinámica cuántica. En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados. Esto significa que el vacío theta es análogo a una fundón de Bloch* en un cristal.
Se puede derivar tanto como un resultado general o bien usando técnicas de instantón. Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido.
Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.

La Naturaleza, siempre nos asombra
Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos pero que tampoco sabemos, en realidad, a que son debidos. Si, sabemos ponerles etiquetas como, por ejemplo, la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio y, con mayor frecuencia, en los elementos que conocemos como transuránidos.
A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de ruptura, sobre pasando a la emisión de partículas alfa.
emilio silvera
















 Totales: 74.997.347
Totales: 74.997.347 Conectados: 54
Conectados: 54























