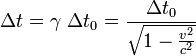Cuando por primera vez se puso este trabajo, dio lugar a comentarios que nos llevan hasta la realidad de hasta donde, resulta para nosotros incomprensible ese micro mundo de la cuántica, ese “universo” infinitesimal donde ocurren cosas que, no llegamos a comprender.

Sí, existe otro mundo que no vemos pero, ¡está en éste!

La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua.  Es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.

Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.

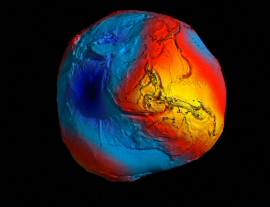
La Gravedad hace que la Tierra se vea como un mapa. Es una vista altamente exagerada, pero ilustra a las claras cómo la atracción gravitatoria que se manifiesta desde la masa de roca bajo nuestros pies no es la misma en todo lugar. La gravedad es más fuerte en áreas amarillas y más débil en las azules. (Imagen tomada por el satélite Goce)

Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.

¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño.  La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10^-33  centímetros, más joven que el Tiempo de Planck, 10^-43 segundos y supere la temperatura de Planck de 10³² grados.  Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.

En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”.  La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes.

Los tiempos cambian y la manera de informar también, lejos nos queda ya aquellos toscos aparatos impresores del pasado, ahora, en espacios muy reducidos, tenemos guardada más información que antes había en una colección de libros.

Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1.975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros.  Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10^-66 cm².  Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

La información llega a todos los rincones del Mundo

No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas.  Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias.

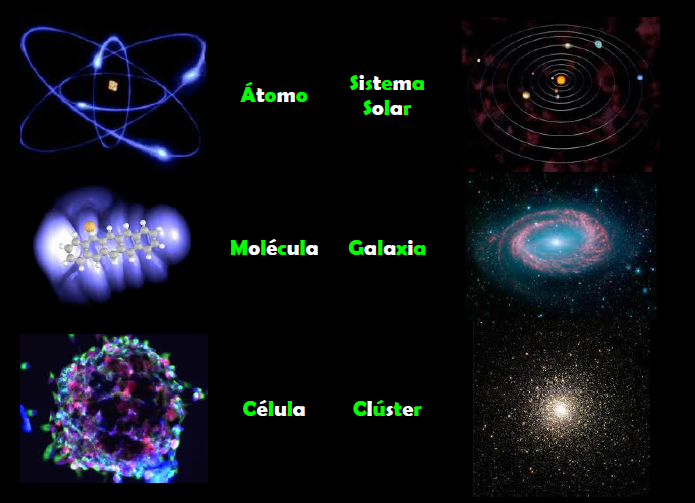
Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y m_protón.

α = 2πe² / hc ≈ 1/137

α_G = (Gm_p2)² / hc ≈ 10^-38

La identificación de constantes adimensionales de la naturaleza como a (alfa) y a_G, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro.

Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala.  La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.

Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck).  Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos. Con los adelantos actuales, estudiando la luz lejana de cuásares muy antiguos, se estudia si la constante de estructura fina (α) ha variado con el paso del tiempo.

El Universo es muy grande, inmensamente grande y, probablemente, todo lo que nuestras mentes puedan imaginar podrá exisitr en alguna parte de esas regiones perdidas en las profundidades cósmicas, en los confines del Espacio- Tiempo, en lugares ignotos de extraña belleza en los que otros mundos y otras criaturas tendrán, su propio habitat que, siendo diferente al nuestro, también, sus criaturas, estarán buscando el significado de las leyes del Universo.

emilio silvera

[?]

Conexiones sin fin que nos llevan a tener consciencia de Ser

El Tiempo: creador de Historias.

El Tiempo, aunque a ciencia cierta no sabemos lo que es, sí sabemos que nos permite contar historias de hechos pasados, buscar las huellas que dejaron en nuestro mundo los cambios habidos en la Naturaleza, y, durante su inexorable transcurrir, van pasando cosas, se están produciendo cambios, y, la Entropía convierte lo nuevo en viejo, mientras que, esa otra clase de Entropía negativa, crea nuevas estrellas, nuevos mundos y nuevas criaturas.

Pero esas son otras historias y, el día de hoy hablaremos del…

¡Preludio a la relatividad! -Las ecuaciones de Lorentz-Fitzgerald- Éste último pensaba y decía cosas comos estas:

 

 

 

          George FitzGerald

 

“… la telegrafía debe mucho a Euclides y otros geómetras puros, al griego y al árabe que fueron matemáticos magistrales que inventaron nuestra escala de numeración y el álgebra, de Galileo y Newton, que fundaron la dinámica, para que Newton y Leibniz inventaran el cálculo, para que Volta descubriera la galvánica bobina, a Oersted quien descubrió la acción magnética de las corrientes, que a Ampère descubriera las leyes de su acción, a Ohm que descubrió la ley de la resistencia de los cables, a Wheatstone, de Faraday, a Lord Kelvin, a Clerk Maxwell, Hertz a… Sin los descubrimientos, invenciones, y las teorías científicas resumen de estos hombres la telegrafía y otras maravillas y conocimientos…  ¡serían imposibles ahora!”

    Hendrik Antoon Lorentz

Se le deben importantes aportaciones en los campos de la termodinámica, la radiación, el magnetismo, la electricidad y la refracción de la luz.  Formuló conjuntamente con George Francis FitzGerald una teoría sobre el cambio de forma de un cuerpo como resultado de su movimiento; este efecto, conocido como “contracción de Lorentz-FitzGerald”, cuya representación matemática de ella es conocida con el de transformación de Lorentz,  fue una más de las numerosas contribuciones realizadas por Lorentz al desarrollo de la teoría de la relatividad.

Fue, al igual que Henri Poincaré,  uno de los primeros en formular las bases de la teoría de la relatividad(frecuentemente atribuida primaria o solamente a Albert Einstein).  Fue ganador del Premio Nobel de Física en 1902, junto con su pupilo Pieter Zeeman,  por su investigación conjunta sobre la influencia del magnetismo en la radiación, originando la radiación electromagnética.  fue premiado con la Medalla Rumford en 1908 y la Medalla Coplay en 1918. Lorentz era hombre humilde y sencillo y le gustaba resaltar los logros de los demás:

 

 

 

Michael Faraday

 

“Como es probable que sepas, gran parte de nuestro conocimiento sobre la electricidad y el magnetismo se basa en los experimentos ingeniosísimos realizados por Michael Faraday en la primera parte del siglo XIX. Faraday era un experimentador genial, y descubrió numerosos fenómenos desconocidos hasta entonces, como la mutua. Estableció diversas leyes, pero no pudo elaborar una teoría global acerca del electromagnetismo porque sus conocimientos matemáticos no iban más allá de la trigonometría: hacía falta un teórico capaz de amalgamar el conocimiento adquirido por Faraday y otros experimentadores, como Hans Christian Ørsted, en una teoría general”.

Ese teórico era otro genio, James Clerk Maxwell, que estableció un conjunto de cuatro ecuaciones diferenciales bellísimas que describían de una manera extraordinariamente precisa los resultados de casi todos los experimentos de Faraday, Ørsted y compañía. Lo más sorprendente, el propio Maxwell y sus contemporáneos, fue una de las consecuencias inevitables de sus ecuaciones: la existencia de perturbaciones del campo eléctrico y el magnético que se propagaban por el espacio.”

 

 

A la contracción, Einstein le dio un marco teórico en la teoría especial de la relatividad. En teoría, un objeto de longitud l₀ en reposo en un sistema de referencia parecerá, un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud , donde c es la velocidad de la luz. La hipótesis original atribuía contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.

 

 

Si no alcanza esa velocidad, nunca podrá escapar de la Gravedad de la Tierra

 

Un objeto que se moviera a 11,2 Km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 Km/s (la mitad de la velocidad de la luz) sería del 15%; a 262.000 Km/s (7/8 de la velocidad de la luz), del 50%. Es decir, que una regla de 30 cm que pasara ante nuestra vista a 262.000 Km/s nos parecería que mide sólo 15’24 cm, siempre y cuando conociéramos alguna manera para medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 Km/s en números redondos, su longitud en la dirección del movimiento sería cero. Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse el universo.

 

 

               Experimento conocido de Michelson-Morley

Todo aquello fue posible gracia a que en 1893, el físico irlandés George Francis FitzGerald emitió una hipótesis explicar los resultados negativos del experimento conocido de Michelson-Morley.  Adujo que toda materia se contrae en la dirección del movimiento, y que esa contracción es directamente proporcional al ritmo (velocidad) del movimiento.

Según tal interpretación, el interferómetro se quedaba corto en la dirección del “verdadero” movimiento terrestre, y lo hacía precisamente en una cantidad que compensaba con toda exactitud la diferencia de distancias que debería recorrer el rayo luminoso.  Por añadidura, todos los aparatos medidores imaginables, incluyendo los órganos sensoriales humanos, experimentarían ese mismo fenómeno.

Parecía como si la explicación de FitzGerald insinuara que la Naturaleza conspiraba con objeto de impedir que el hombre midiera el movimiento absoluto, lo cual introducía un efecto que anulaba cualquier diferencia aprovechable para detectar dicho movimiento.

Este asombroso fenómeno recibió el de “contracción de FitzGerald”, y su autor formuló una ecuación para el mismo que, referido a la contracción de un cuerpo móvil, fue predicha igualmente, y de manera independiente, por H.A.Lorentz (1853-1928) de manera que, finalmente, se quedaron unidas como “Contracción de Lorentz-Fitz Gerald”.

 

 

 

 

El efecto Fitzgerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas como las ecuaciones Lorentz-Fitzgerald.

 

 

 

 

La dilatación del tiempo es el fenómeno predicho por la teorçia de la relatividad,  por el cual un observador observa que el reloj de otro (un reloj físicamente idéntico al suyo) está marcando el tiempo a un ritmo menor que el que mide su reloj. Esto se suele interpretar normalmente como que el tiempo se ha ralentizado para el otro reloj, pero eso es cierto solamente en el contexto del sistema de referencia del observador. Localmente, el tiempo siempre está pasando al mismo ritmo. El fenómeno de la dilatación del tiempo se aplica a cualquier proceso que manifieste cambios a través del tiempo.

fórmula para determinar la dilatación del tiempo en la relatividad especial es:

Donde:

 

 es el intervalo temporal entre dos eventos co-locales para un observador en algún sistema de referencia inercial. (por ejemplo el número de tic tacs que ha hecho su reloj)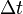

 es el intervalo temporal entre los dos mismos eventos, tal y como lo mediría otro observador moviéndose inercialmente con velocidad v, respecto al primer observador

 es la velocidad relativa entre los dos observadores

 la velocidad de la luz y

es el también conocido como factor de Lorentz

De esta manera la duración del un ciclo de reloj del reloj que se mueve se ha incrementado: esta “funcionando más despacio”. Según lo indicado las transformaciones de Lorentz  pueden ser utilizadas para casos más generales.

Postulados de la Relatividad Especial

 

• Primer postulado:  Principio especial de relatividad: Las leyes de la física son las mismas en todos los sistemas de referencia inerciales. En otras palabras, no existe un sistema inercial de referencia privilegiado, que se pueda considerar como absoluto.

• Segundo postulado: Invariancia de c: La velocidad de la luz en el vacío es una constante universal, c, que es independiente del movimiento de la fuente de luz.

 

Aquí podemos ver el tiempo que tarda la luz en llegar desde la Tierra a la Luna situada a más de 380.000 Km. Desde el Sol, situado a unos 150 millones de kilómetros, la luz tarda poco más de 8 minutos en llegar a nosotros, es decir, si el Sol desapareciera, nos daríamos cuenta 8 minutos más tarde.

 Einstein que se apropió de aquella idea (de Lorentz) y, además, la amplió al contraer también el Tiempo. La contracción de la longitud ha sido verificada en el diseño, por ejemplo, del acelerador lineal de la Universidad de Stanford. Las partículas salen con una velocidad v = 0,999975c, por tanto, metro de tubo acelerador es “visto” por los electrones como 144 metros. Si, según la expresión anterior, un cuerpo con masa se moviera a la velocidad c desaparecería por contracción de su longitud para un observador en reposo, lo cual refuerza el carácter inalcanzable de velocidad. Si los objetos con masa alcanzan este límite de velocidad la estructura básica de la realidad se desvanece. Por otra parte, vemos que cualquier influencia que afecte al tiempo también lo hará con el espacio. Esto no nos debe de extrañar, ya que ambas magnitudes se encuentran íntimamente relacionadas por lo único que se nos mantiene invariable: la velocidad de la luz. En relatividad hablamos de espacio-tiempo ya que son inseparables.

A la contracción, Einstein, le dio un marco teórico en la teoría especial de la relatividad. En teoría, un objeto de longitud /0 en reposo en un sistema de referencia parecerá, para un observador en otro sistema de referencia que se mueve con velocidad relativa v con respecto al primero, tener longitud /0 , donde c es la velocidad de la luz. La hipótesis original atribuía esta contracción a una contracción real que acompaña al movimiento absoluto del cuerpo. La contracción es en cualquier caso despreciable a no ser que v sea del mismo orden o cercana a c.

Un objeto que se moviera a 11 km/s (la velocidad de escape de nuestro planeta) experimentaría sólo una contracción equivalente a 2 partes por cada 1.000 millones en el sentido del vuelo. Pero a velocidades realmente elevadas, tal contracción sería sustancial. A unos 150.000 km/seg. (la mitad de la velocidad de la luz, c), sería del 15%; a 262.000 km/seg. (7/8 de la velocidad de la luz), del 50% Es decir, que una regla de 30 cm. que pasara ante nuestra vista a 262.000 km (seg., nos parecería que mide sólo 15’54 cm…, siempre y cuando conociéramos alguna manera medir su longitud en pleno vuelo. Y a la velocidad de la luz, es decir, 300.000 km/seg., en números redondos, su longitud, en la dirección del movimiento, sería cero.  Puesto que, presuntamente, no puede existir ninguna longitud inferior a cero, se deduce que la velocidad de la luz en el vacío es la mayor que puede imaginarse en el Universo. (Pero ¿existir también?).

El físico holandés Hendrik Antón Lorentz, como hemos dicho, promovió ésta idea pensando en los rayos catódicos (que ocupaban su actividad por aquellas fechas), se hizo el siguiente razonamiento: si se comprimiera la carga de una partícula reducir su volumen, aumentaría su masa.  Por consiguiente, una partícula voladora, escorzada en la dirección de su desplazamiento por la contracción de Fitz Gerald, debería crecer en términos de masa.

Un objeto que corra a velocidades cercanas a la de la luz, verá incrementada su masa. Haces de muones lanzados por el LHC a velocidades relativistas, incrmentaron su masa diez veces cuando estaban cerca de c. Lo cierto es que, como la velocidad de la luz es el límite impuesto por el Universo para la velocidad, cuando el objeto se va acercando a dicho límite, se va frenando y la energía de inercia se convierte en masa. Ya sabéis: E = mc² .

Lorentz presentó una ecuación sobre el acrecentamiento de la masa, que resultó muy similar a la ecuación FitzGerald sobre el acortamiento. A 149.637 kilómetros por segundo, la masa de un electrónaumentaría en un 15%; a 262.000 km/seg., en un 100% (es decir, la masa se duplicaría); y a la velocidad de la luz, su masa sería infinita.  Una vez más pareció que no podría haber ninguna velocidad superior a la de la luz, pues, ¿cómo podría ser una masa mayor que infinita? El efecto FitzGerald sobre longitudes y el efecto Lorentz sobre masas mantuvieron una conexión tan estrecha que aparecieron a menudo agrupadas las “ecuaciones Lorentz-FitzGerald.”

Mientras que la contracción FitzGerald no podía ser objeto de mediciones, el efecto Lorentz sobre masas si podía serlo…, aunque indirectamente. De hecho, el muón, tomó 10 veces su masa original fue lanzado, a velocidades relativistas, en el acelerador de partículas, lo que confirmó la ecuación de Lorentz. Los experimentos posteriores, han confirmado las ecuaciones de ambos: a velocidades relativistas, las longitudes se contraen y las masas se incrementan.

                                                                 Nada puede viajar a la velocidad de la luz

Como es conocido por todos, Einstein adoptó estos descubrimientos y los incorporó a su teoría de la relatividad especial que, aunque mucho más amplia, recoge la contracción de FitzGerald y el aumento de la masa de Lorentz cuando se alcanzan grandes velocidades.

¡Qué cosas!

Algunas veces pienso que, los artistas en general, y los poetas en particular, tendrían que adaptar e incluir a sus esquemas artísticos y poéticos, los adelantos científicos, para asimilarlos en las diversas expresiones y sentimientos que serán después puestos al servicio del consumo humano.

Estos adelantos científicos serían así coloreados con las pasiones humanas y transformadas, de alguna , en la sangre, y por qué no, los sentimientos de la naturaleza humana.

Posiblemente, de haberlo hecho así, el grado general de conocimiento sería mayor.

emilio silvera

[?]

                      Hallado un sistema planetario similar al nuestro a tan solo 10 años luz

Noticias NASA: La vida podría estar más cerca de lo que podríamos pensar. Otros sistemas planetarios pueden reunir las condiciones para ello. En un radio de unos 20 años luz del Sol, pueden encontrarse grandes sorpresas.

El observatorio SOFIA de la NASA, emplazado en un avión ‘jumbo’ adaptado, ha confirmado la presencia de un sistema planetario con una arquitectura parecida a la del nuestro a 10,5 años luz. El estudio ha sido publicado en ‘The Astronomical Journal’.

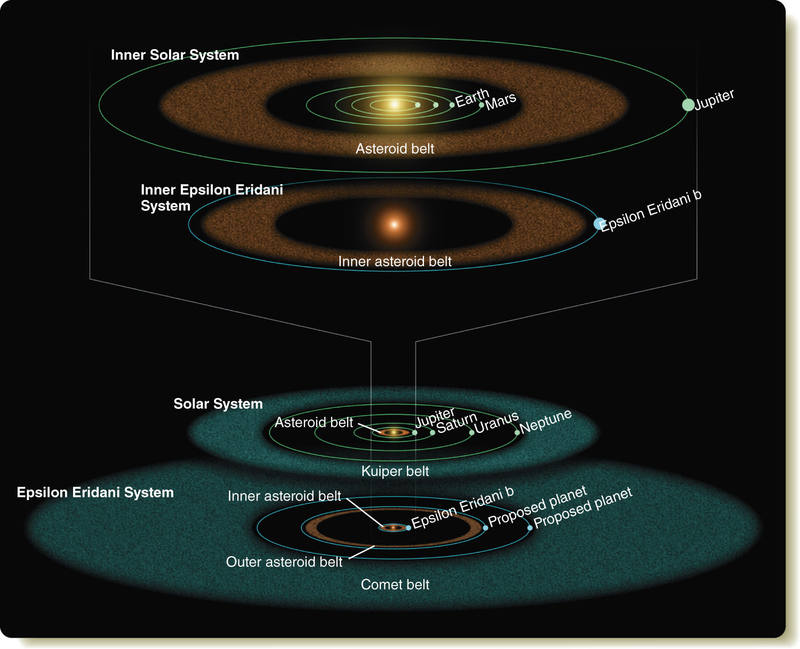
Ubicado en la constelación de Eridanus del hemisferio sur, la estrella Epsilon Eridani, eps Eri para abreviar, es el sistema planetario más cercano alrededor de una estrella similar al sol temprano. Es una ubicación privilegiada para investigar cómo los planetas se forman alrededor de estrellas como nuestro sol, y también es la ubicación de la estación espacial Babylon 5 en la serie de televisión de ciencia ficción del mismo nombre.

Estudios previos indican que Eps tiene un disco de desechos, que es el nombre que los astrónomos dan a los restos de material que sigue orbitando una estrella después de que la construcción planetaria haya terminado. Los escombros pueden tomar la forma de gas y polvo, así como pequeños cuerpos rocosos y helados. Los discos de desecho pueden ser discos anchos y continuos o concentrados en cinturones de escombros, similares al cinturón de asteroides de nuestro sistema solar y el Cinturón de Kuiper –la región más allá de Neptuno, donde residen cientos de miles de objetos rocosos.

Además, las mediciones cuidadas del movimiento de Eps Eri indica que un planeta con casi la misma masa que Júpiter circunda la estrella a una distancia comparable a la distancia de Júpiter del Sol.

[?]