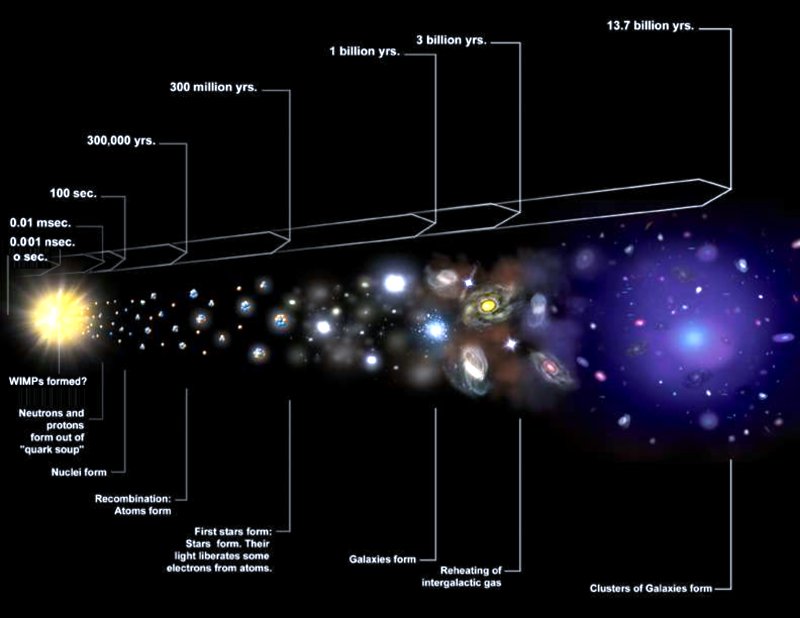
Está claro que, los estudiosos de la época antigua estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.

Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1637.

Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden.
Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro” “fantasma!.


Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.
Le surgieron y se planteó algunas inquietudes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?

En 1678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.
Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Peor la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sobras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿cuál era esa mecánica ondulatoria?

Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular, de Newton, fue, con mucho, la más popular, en parte, porque la respaldó el famoso nombre de su autor. Pero hacia 1801, un físico y médico ingles, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos. Si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. Pero no fue esto lo que descubrió Young. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras. Pareció incluso que, en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.
Sería fácil explicarlo mediante la teoría ondulatoria. La banda luminosa representaba el refuerzo presado por las ondas de un rayo a las ondas del otro. Dicho de otra manera: Entraba “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.

Considerando la anchura de las bandas y la distancia entre los dos edificios por los que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. (Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Angströn. Esta unidad, denominada, en honor a su autor Ángstrom (Á), es la cienmillonésima parte de un centímetro. Así, pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Á, y la de la luz violeta, a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.)
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si éste no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior de una onda luminosa y, por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de la onda luminosa (por ejemplo, los virus y otras partículas submicroscópicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.

Thomas Young Augustin Fresnel
Un físico francés, Augustin-Jean Fresnel, fue quien demostró por vez primera, en 1818, que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de disfracción” actúan como una serie de minúsculos obtáculos, que se refuerzan entre si. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.

Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso: los rayos espectrales. El físico americano Henry Augustus Rowlane ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.

No sólo se aceptó las existencias de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalterable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento, denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.
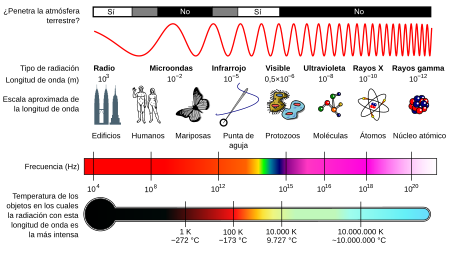
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuáles aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.
En 1960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de longitud. Entonces se restableció la longitud de metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumento mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
Ahora, después de todo esto, sabemos algo más sobre la luz.
Pero ¿qué pasa con su velocidad?
¡Veámoslo!
LA VELOCIDAD DE LA LUZ

Está claro que, la luz se desplaza a enormes velocidades. Si pulsamos el interruptor de apagado de la lámpara de nuestro salón, todo queda a oscuras de manera instantánea.
La velocidad del sonido es más lenta, por ejemplo, si vemos a un leñador que está cortando leña en un lugar alejado de nosotros, sólo oiremos los golpes momentos después de que caiga el hacha. Así, pues, el sonido tarda cierto tiempo en llegar a nuestros oídos. En realidad es fácil medir la velocidad de su desplazamiento: unos 1.206 km/h en el aire y a nivel del mar.

Poca seguridad podía dar aquel rústico medio
Galileo fue el primero en intentar medir la velocidad de la luz. Se colocó en lo alto de una colina, mientras que su ayudante, se situaba en otro lugar alto de la colina vecina; luego sacó una linterna encendida: tan pronto como su ayudante vió la luz, hizo una señal con otra linterna. Galileo repitió el experimento a distancias cada vez mayores, suponiendo que el tiempo requerido por su ayudante para responder mantendría una uniformidad constante, por lo cual, el intervalo entre la señal de su propia linterna y la de su ayudante representaría el tiempo empleado por la luz para recorrer cada distancia. Aunque la idea era lógica, la luz viajaba demasiado aprisa como para que Galileo pudiera percibir las sutiles diferencias con un método tan rudimentario.

Esta es la distancia que recorre la luz desde el Sol hasta la Tierra… ¡150.000.000 Km.!
En 1676, el astrónomo danés Olau Roemer logró cronometrar la velocidad de la luz a escala de distancias astronómicas. Estudiando los eclipses de Júpiter en sus cuatro grandes satélites, Roemer observó que el intervalo entre eclipses consecutivos era más largo cuando la Tierra se alejaba de Júpiter, y más corto cuado se movía en su órbita hacía dicho astro. Al parecer, la diferencia entre las duraciones del eclipse reflejaba la diferencia de distancias entre la Tierra y Júpiter. Y trataba, pues, de medir la distancia partiendo del tiempo empleado por la luz para trasladarse desde Júpiter hasta la Tierra. Calculando aproximadamente el tamaño de la órbita terrestre y observando la máxima discrepancia en las duraciones del eclipse que, según Roemer, representaba el tiempo que necesitaba la luz para atravesar el eje de al órbita terrestre, dicho astrónomo computó la velocidad de la luz. Su resultado, de 225.000 km/s., parece excelente si se considera que fue el primer intento, y resultó bastante asombroso como para provocar la incredulidad de sus coetáneos.
Sin embargo, medio siglo después se confirmaron los cálculos de Roemer en un campo totalmente distinto. Allá por 1728, el astrónomo británico James Bradley descubrió que las estrellas parecían cambiar de posición con los movimientos terrestres; y no por el paralaje, sino porque la traslación terrestre alrededor del Sol era una fracción mensurable (aunque pequeña) de la velocidad de la luz. La analogía empleada usualmente es la de un hombre que camina con el paraguas abierto bajo un temporal. Aun cuando las gotas caigan verticalmente, el hombre debe inclinar hacia delante el paraguas, porque ha de abrirse paso entre las gotas.

Cuanto más acelere su paso, tanto más deberá inclinar el paraguas. De manera semejante la Tierra avanza entre los ligeros rayos que caen desde las estrellas, y el astrónomo debe inclinar un poco su telescopio y hacerlo en varias direcciones, de acuerdo con los cambios de la trayectoria terrestre (no olvidemos que nuestro planeta Tierra, es como una enorme nave espacial que nos lleva en un viaje eterno, alrededor del Sol, a la velocidad de 30 km/s. + -) Mediante ese desvío aparente de los astros (“aberración de la luz”), Bradley pudo evaluar la velocidad de la luz y calcularla con gran precisión.
Sus cálculos fueron de 285.000 km/s, bastante más exacto que los de Roemer, pero aún un 5’5% más bajos.
Poco a poco, con medios tecnológicos más sofisticados y más conocimientos matemáticos, los científicos fueron obteniendo medidas más exactas aún, conforme se fue perfeccionando la idea original de Galileo y sus sucesores.
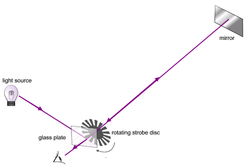
Esquema del dispositivo utilizado por Fizeau en 1849
En 1849, el físico francés Armand-Hippolyte-Louis Eizeau ideó un artificio mediante el cual se proyectaba la luz sobre un espejo situado a 8 km de distancia, que devolvía el reflejo al observador. El tiempo empleado por la luz en su viaje de ida y vuelta no rebasó apenas la 1/20.000 de segundo, por Fizeau logró medirlo colocando una rueda dentada giratoria en la trayectoria del rayo luminoso. Cuando dicha rueda giraba a cierta velocidad, regulada, la luz pasaba entre los dientes y se proyectaba contra el siguiente, al ser devuelta por el espejo; así, Fizeau, colocado tras la rueda, no pudo verla. Entonces se dio más velocidad a la rueda, y el reflejo pasó por la siguiente muesca entre los dientes, sin intercepción alguna. De esa forma, regulando y midiendo la velocidad de la rueda giratoria, Fizeau pudo calcular el tiempo transcurrido y, por consiguiente, la velocidad a que se movía el rayo de luz.

Animación del Péndulo de Foucault oscilando en el hemisferio sur
Un año más tarde, Jean Foucault (quien realizaría poco después su experimento con los péndulos) precisó más estas medidas empleando un espejo giratorio en ve de una rueda dentada. Entonces se midió el tiempo transcurrido desviando ligeramente el ángulo de reflexión mediante el veloz espejo giratorio. Foucault obtuvo un valor de la velocidad de la luz de 300.883 km/s. También, el físico francés utilizó su método para determinar la velocidad de la luz a través de varios líquidos. Averiguó que era notablemente inferior a la alcanzada en el aire. Esto concordaba también con la teoría ondulatoria de Huyghens.

Interferómetro de Michelson:
A – Fuente de luz monocromática
B – Espejo semirreflectante
C – Espejos
D – Diferencia de camino.
Michelson fue más preciso aún en sus medidas. Este autor, durante cuarenta años largos, a partir de 1879, fue aplicando el sistema Fizeau-Foucault cada vez con mayor refinamiento, para medir la velocidad de la luz. Cuando se creyó lo suficientemente informado, proyectó la luz a través de vacío, en vez de hacerlo a través del aire, pues este frena ligeramente su velocidad, y, empleó para ello tuberías de acero cuya longitud era superior a 1’5 km. Según sus medidas, la velocidad de la luz en el vacío era de 299.730 km(seg. (sólo un 0’006% más bajo). Demostraría también que todas las longitudes de ondas luminosas viajan a la misma velocidad en el vacío.

Desde Galileo con sus lámparas, cada vez se han utilizado aparatos más sofisticados para medir la velocidad de la luz, y, finalmente, se consiguió medirla …
En 1972, un equipo de investigadores bajo la dirección de Kenneth M. Eveson efectuó unas mediciones aún más exactas y vio que la velocidad de la luz era de 299.727’74 km/seg. Una vez se conoció la velocidad de la luz con semejante precisión, se hizo posible usar la luz, o por lo menos formas de ella, para medir distancias.
Aunque para algunos resulte alto tedioso el tema anterior, no he podido resistirme a la tentación de exponerlo, así podrá saber algo más sobre la luz y, habrán conocido a personajes que hicieron posible el que ahora nosotros, la conozcamos mejor.

Podría continuar, hasta el final de este trabajo, hablando de la luz y sus distintas formas o aplicaciones: ondas de luz a través del espacio, de cómo se transmite la luz en el “vacío”, nos llega a través del espacio desde Galaxias situadas a miles de millones de años luz; las líneas de fuerzas electromagnéticas de Faraday y Maxwell de campos eléctricos y magnéticos cambiantes (todo ello explicado en un simple conjunto de cuatro ecuaciones, que describían casi todos los fenómenos referentes a esta materia electromagnética), o de los enigmas aún por descubrir (aunque predichos).
Este comentario ya se hizo algo largo y, desde luego, mio último deseo es aburrir al lector, así que dejaremos para otro día una continuación sobre lo que es la luz, aunque, eso sí, no me quiero despedir sin dejar claro que, también todos nosotros somos… ¡LUZ!
emilio silvera


6 de agosto del 2016 (DG). La nave espacial para la caza de asteroides de la NASA reveló la existencia de cientos de objetos cercanos a la Tierra (NEOs) de los cuales 72 fueron recién detectados y ocho de los 72 fueron clasificados como asteroides potencialmente peligrosos para la tierra
La más destructiva intensificación temporal de los normalmente suaves flujos de energía geotectónica – erupciones volcánicas o terremotos extraordinariamente potentes – o de energía atmosférica – vientos o lluvias anormalmente intensas –, parecen irrelevantes cuando se comparan con las repetidas colisiones del planeta con cuerpos extraterrestres relativamente grandes.


La Tierra está siendo bombardeada continuamente por invisibles partículas microscópicas de polvo muy abundantes en todo el Sistema Solar, y cada treinta segundos se produce un choque con partículas de 1 mm de diámetro, que dejan un rastro luminoso al autodestruirse en la atmósfera. También son relativamente frecuentes los choques con meteoritos de 1 metro de diámetro, que se producen con una frecuencia de, al menos, uno al año.
Pero los impactos, incluso con meteoritos mayores, producen solamente efectos locales. Esto es debido a que los meteoritos que deambulan por la región de asteroides localizada entre Marte y Júpiter están girando alrededor del Sol en el mismo sentido que la Tierra, de manera que la velocidad de impacto es inferior a 15 Km/s.

El cráter de Arizona, casi perfectamente simétrico, se formó hace 25.000 años por el impacto de un meteorito que iba a una velocidad de 11 Km/s, lo que representa una potencia cercana a 700 PW. Estas gigantescas liberaciones de energías palidecen cuando se comparan con un choque frontal con un cometa típico. Su masa (al menos de 500 millones de toneladas) y su velocidad relativa (hasta 70 Km/s) elevan su energía cinética hasta 1022 J. Aunque se perdiera un diez por ciento de esta energía en la atmósfera, el impacto sería equivalente a una explosión de unas 2.500 bombas de hidrógeno de 100 megatones. Está claro que un fenómeno de estas características produciría impresionantes alteraciones climatológicas. Sin embargo, no es seguro y sí discutible que un impacto parecido fuese la causa de la extinción masiva del cretácico, siendo lo más probable, si tenemos en cuenta el periodo relativamente largo en que se produjo, que se podría explicar por la intensa actividad volcánica de aquel tiempo.


Aproximadamente, cada cincuenta o sesenta millones de años se produce una colisión con un cometa, lo que significaría que la biosfera, que ha evolucionado durante cuatro mil millones de años, ha debido superar unos cuarenta impactos de este tipo. Está claro que ha salido airosa de estas colisiones, ya que aunque haya sido modificada, no ha sido aniquilada.

Se cree que la explosión de supernovas “cercanas” influyeron en la biosfera de nuestro planeta
Igualmente, la evolución de la biosfera ha sobrevivido a las explosiones altamente energéticas de las supernovas más “cercanas”. Dado que en nuestra galaxia se produce por término medio la explosión de una supernova cada 50 años, el Sistema Solar se encuentra a una distancia de 100 parsecs de la explosión cada dos millones de años y a una distancia menor de 10 parsecs cada dos mil millones de años. En este último caso, la parte alta de la atmósfera se vería inundada por un flujo de rayos X y UV de muy corta longitud de onda, diez mil veces mayor que el flujo habitual de radiación solar, lo que implica que la Tierra recibiría, en unas pocas horas, una dosis de radiación ionizante igual a la que recibe anualmente. Exposiciones de 500 roentgens son letales para la mayoría de los vertebrados y, sin embargo, los diez episodios de esta magnitud que se han podido producir en los últimos 500 millones de años no han dejado ninguna consecuencia observable en la evolución de la biosfera.

Lo cierto es que no tenemos tan cerca a ninguna estrella hipergigante que, al explotar como supernova, nos pueda inquietar, su radio de acción y vientos estelares del evento no llegarían a nosotros… con peligro
Si suponemos que una civilización avanzada podría preparar refugios para la población durante el año que transcurre ente la llegada de la luz y la llegada de la radiación cósmica, se encontraría con la inevitable dosis de 500 roentgens cada mil millones de años, tiempo suficiente para permitir el desarrollo de una sociedad cuyo conocimiento le sirviera para defenderse de un flujo tan extraordinario y de consecuencias letales.
emilio silvera

La inmensa mayoría de los terremotos se originan en los procesos geotectónicos a gran escala que crean, hacen chocar y hunden en las zonas de subducción, las placas oceánicas. No menos del 95 por ciento de todos los terremotos se concentran a lo largo de los bordes de las placas y cerca de nueve décimas partes de éstos se localizan en el cinturón Circum-Pacífico, donde las placas, que son relativamente rápidas, están colisionando o deslizándose contra las placas continentales más pesadas. La mayor parte del resto de terremotos están asociados a los puntos calientes, generalmente señalados por volcanes en actividad.

En conjunto, los terremotos representan una fracción muy pequeña de la energía liberada por los procesos tectónicos de la Tierra. Desde 1900, en los mayores terremotos se han liberado anualmente una energía media cercana a los 450 PJ, que no supone más del 0’03 por ciento del flujo total de calor terrestre. La liberación anual de energía sísmica de todos los terremotos que se han medido alcanza unos 300 GW, que sumada a la energía de esfuerzo invertida en deformaciones irreversibles y al calor generado por fricción a lo largo de las fallas, daría un total próximo a 1 TW, lo cual representa solamente un 2’5 por ciento del flujo de calor global.
Pero este recuento total nos dice poco de la liberación de energía y de la potencia de un solo terremoto. Aunque la mayoría son tan débiles que pasan desapercibidos para las personas, cada año se producen terremotos terriblemente destructivos, que durante el siglo XX han causado más víctimas mortales que las inundaciones, ciclones y erupciones volcánicas juntas.
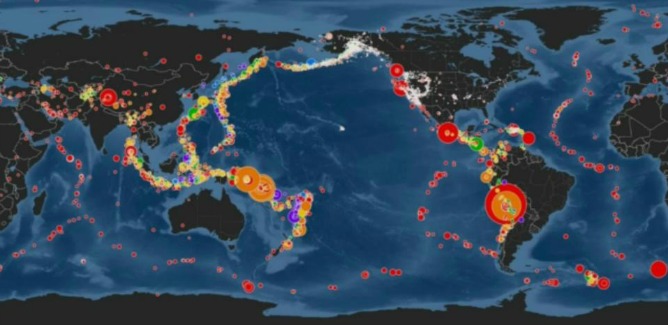
La energía de estos terremotos se puede calcular a partir de la energía cinética de las ondas sísmicas generadas por la energía liberada en el esfuerzo de la deformación del suelo, pero rara vez se realizan estos cálculos directamente. Lo más frecuente es deducir la energía del terremoto a partir de la medida de su magnitud o de su momento. La medida típica de la magnitud de un terremoto fue establecida por Charles Richter en 1935, como el logaritmo decimal de la máxima amplitud (en micrómetros) registrada con un sismómetro de tensión estándar (Word-Anderson) a 100 Km de distancia del epicentro del temblor.

Desde que en 1942, Richter publicó la primera correlación entre la magnitud de energía sísmica liberada en un temblor, su trabajo (como por otra parte, es de lógica) ha sufrido numerosas modificaciones. La conversión sigue la forma estándar log10 E = a + bM, donde E es la energía liberada en forma de ondas sísmicas (en ergios), M es la magnitud de Richter, y a y b son los coeficientes empíricos que varían entre 6’1 – 13’5 y 1’2 – 2 respectivamente. Otras conversiones alternativas permiten obtener la energía liberada a partir del momento del terremoto, que se define como el producto de la rigidez por el desplazamiento medio de la falla y por la superficie media desplazada.

Los mayores terremotos registrados tienen magnitudes Richter comprendidas entre 8 y 8’9, con liberación de energía sísmica entre 48 PJ y 1’41 EJ. Todos hemos oído en alguna ocasión algún comentario sobre el terremoto de San Francisco de 1906, donde los cálculos basados en tres métodos utilizados en el esfuerzo dieron valores tan distintos como 9’40 y 175 PJ, y con método cinético se obtuvo 2’5 PJ.
Los terremotos, por ser a la vez de breve duración y estar limitados espacialmente, desarrollan potencias y densidades de potencia extraordinariamente altas. La potencia de un temblor de magnitud 8 en la escala de Richter que durase solamente medio minuto, sería de 1’6 PW, y si toda esta potencia estuviera repartida uniformemente en un área de 80 Km de radio, la densidad de potencia sería tan elevada como 80 KW/m2.

Obviamente, tales flujos pueden ser terriblemente destructivos, pero ni las pérdidas de vidas humanas ni los daños materiales que ocasionan los temblores están correlacionados de una manera sencilla con la energía liberada. La densidad de población o de industrias, así como la calidad de las construcciones, constituyen un factor muchísimo más importante para determinar la mortandad o el impacto económico de los mismo. Por ejemplo, el coste en vidas humanas del gran terremoto japonés que en 1923 arrasó Tokio, donde existía una alta densidad de casas de madera, fue unas 200 veces más elevado que el terremoto de San Francisco de 1906 en el que se liberó cuatro veces más energía. También aquí salen perdiendo, como siempre, los pobres.
Por otra parte, no podemos olvidar que la superficie del globo terrestre está dominada por las aguas, y los seres humanos viven en la Tierra seca. Sin embargo, vienen los tsunamis. La predicción de estas catástrofes continúa siendo imposible. Se tienen datos, se localizan las zonas de más frecuencia, y conocen las fallas de desgarre y las inversas, los ciclos, etc., pero el conocimiento es aún escaso para prevenir dónde y cuándo se producirán temblores.

Las olas sísmicas que se pueden provocar por terremotos submarinos se propagan durante miles de kilómetros a velocidades de 550 – 720 Km/h, perdiendo en su viaje muy poca potencia. Estas olas, prácticamente invisibles en el mar, se levantan hasta una altura de 10 metros en agua poco profundas y pueden llegar a golpear las costas con intensidades de potencia en superficie vertical de hasta 200 – 500 MW/m2, y con impactos horizontales de intensidad y potencia entre 10 – 100 MW/m2. Son, pues, mucho más potentes que los ciclones tropicales y causan grandes daños tanto materiales como en pérdida de vidas humanas.
emilio silvera
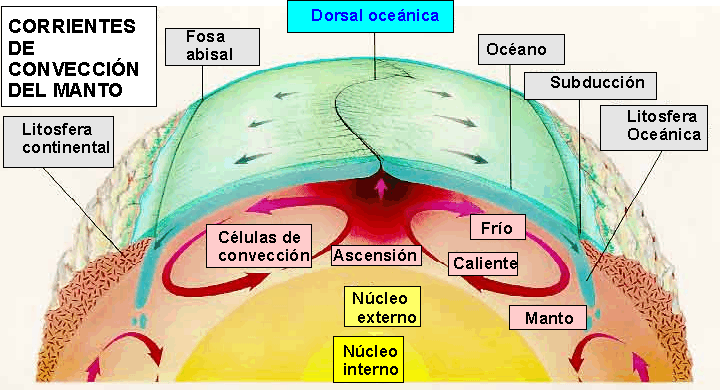
Los grandes accidentes de la superficie terrestre (el fondo marino, los continentes y sus cordilleras) han sido generados por el imparable movimiento de los rígidos bloques de la litosfera. Las grandes placas oceánicas divergen en las crestas dorsales oceánicas, donde surge el magma creando nueva corteza basáltica, que se desliza a lo largo de fallas hasta que finalmente chocan con los bordes continentales donde se hunden en profundas fosas, zonas de subducción, para ser recicladas en el manto. Aunque el recorrido entre la dorsal y la fosa se completa en 107 años, algunas zonas continentales permanecen muy estables, estando cubiertas por rocas cuya edad es casi veinte veces la edad de las más antiguas cortezas marinas, que a su vez, datan de unos doscientos millones de años.

Dondequiera que choquen las relativamente rápidas placas tectónicas oceánicas con las enormes placas continentales, se forman cadenas montañosas en continua elevación. Los ejemplos más espectaculares se subducción y formación montañosa son, respectivamente, la placa del Pacífico sumergiéndose en las profundas fosas del Asia oriental, y el Himalaya, que se eleva por el choque de las placas índica y euroasiática.
En otras zonas de la litosfera, la afloración de rocas calientes del mando debilita inicialmente y agrietan posteriormente la corteza continental, hasta que finalmente, formando nueva corteza oceánica, separan los continentes. Ejemplos de diversos estadios de este proceso son el Mar Rojo, el golfo de Adén y las fracturas del Valle del Rift, en el este de África.

El movimiento de la placa africana es hacia el Norte a unos 2,15 centímetros cada año, lo cual la llevará a unirse al extremo sur de España dentro de 650.000 años, separando el mar Mediterráneo del océano Atlántico.
Este proceso de separación continental parece ser bastante regular. Se observan periodos de formación montañosa por compresión en el intervalo de cuatrocientos a quinientos millones de años, a los que sigue, unos cien millones de años más tarde, un resurgir de la rotura. Esta secuencia se repite en un ciclo supercontinental en el que se alterna la separación de grandes zonas continentales con su agrupamiento.


Imagen de la isla de Hawái desde satélite.
Las plumas de magma que perforan la litosfera también crean focos calientes duraderos que están asociados a los volcanes. Las islas Hawai y la cadena de montañas oceánicas que se extienden desde ellas hasta Kamchatka constituyen la manifestación más espectacular de focos calientes que surgen en medio de la veloz placa del Pacífico, entre los que actualmente se encuentran los ríos continuos de lava del volcán Kilauea y la lenta creación de la futura isla hawaiana de Loihi.

Las enormes plumas de magma que afloran desde las capas profundas del manto han dado origen a grandes superficies de lava, la mayor de las cuales es la meseta oceánica de Ontong Java, que cubre dos millones de kilómetros cuadrados, y la meseta del Decán y la siberiana, que son las mayores formaciones basálticas continentales. La generación de estas extensas formaciones afecta de manera importante a la composición de la atmósfera debido a las grandes emisiones de CO2 y SO2 que las acompañan, y que causan elevaciones de la temperatura troposférica y lluvias ácidas, con los consiguientes efectos cruciales en la biota.

Los procesos energéticos de la geotectónica terrestre son complejos. Incluso resulta todavía incierta la contribución relativa de las fuerzas involucradas en el movimiento de las placas tectónicas. Las dos fuerzas más importantes están asociadas a la convección del material caliente del manto y al hundimiento de las zonas frías, con flotabilidad negativa, de la litosfera oceánica en las zonas de subducción. Este último proceso es debido a diferencias de densidad, máxima a una profundidad de doscientos o trescientos kilómetros, que generan un momento de fuerzas en el manto viscoso responsable de la principal fuerza convectiva.
Las velocidades de las placas, al ser estudiadas, se observa que las que cuentan con una mayor proporción de sus bordes en zonas de subducción se mueven a velocidades de 60 a 90 kilómetros por millón de años, mientras que la velocidad de las placas en las que no hay hundimiento de bloques es inferior a 40 kilómetros por millón de años.

Sin embargo, la contribución de la emisión de material del manto no es despreciable, ya que la considerable energía potencial gravitatoria de extensas zonas de rocas calientes hace que se genere nueva corteza marina en las dorsales oceánicas con una velocidad que es, al menos, tres veces superior a la velocidad con que se genera en los planos abisales.
La combinación de ese “tirar” a lo largo de las zonas de subducción y de “empujar” en las dorsales da lugar a velocidades, para las placas más rápidas, de aproximadamente 20 cm/año durante cortos periodos de tiempo. Entre estas placas que se mueven rápidamente se encuentran no sólo los pequeños bloques como Nazca y Cocos, sino también la enorme placa del Pacífico, lo cual indica que la fuerza de arrastre del manto, proporcional al área y a la velocidad, debe ser relativamente pequeña.
La mayor parte del flujo de calor que se ha medido en la Tierra debe atribuirse a la formación de nueva litosfera oceánica.
emilio silvera

















 Totales: 74.829.189
Totales: 74.829.189 Conectados: 72
Conectados: 72 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en
Clasificado en