Dic
21
Fuerzas y Constantes…¡El Universo!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
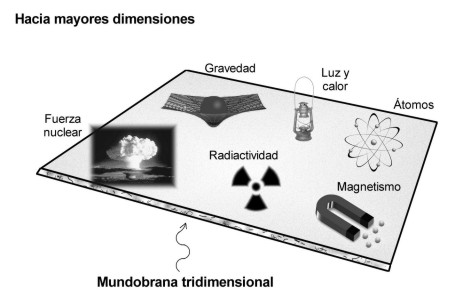
Las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil. Seguramente ese será el motivo por el cual, encontrar al Bosón mediador de la fuerza, el Gravitón, resulta tan difícil.

Muchos han sido los intentos de localizar al gravitón, sin éxito alguno. ¿Será el de arriba? Seguramente no. Sin embargo, aunque no será fácil, debemos seguir la búsqueda del bosón que intermedia en la fuerza gravitacional.
Las fuerzas fundamentales
| Tipo de Fuerza | Alcance en m | Fuerza relativa | Función |
| Nuclear fuerte | <3×10-15 | 1041 | Une Protones y Neutrones en el núcleo atómico por medio de Gluones. |
| Nuclear débil | < 10-15 | 1028 | Es responsable de la energía radiactiva producida de manera natural. Portadoras W y Z– |
| Electromagnetismo | Infinito | 1039 | Une los átomos para formar moléculas; propaga la luz y las ondas de radio y otras formas de energías eléctricas y magnéticas por medio de los fotones. |
| Gravitación | Infinito | 1 | Mantiene unidos los planetas del Sistema Solar, las estrellas en las galaxias y, nuestros pies |

La Fuerza nuclear fuerte es la más potente de las cuatro fuerzas fundamentales. Los núcleos de los átomos están conformados por protones y neutrones que, a su vez están hechos de quarks. Los quarks están confinados dentro de los hnucleones y sujetos por las partículas mediadoras de la fuerza, los Gluones que no permiten que los quarks se separen manteniendo así, el debido equilibrio.
Las constantes fundamentales
| Constante | Símbolo | Valor en unidades del SI |
| Aceleración en caída libre | g | 9,80665 m s-2 |
| Carga del electrón | e | 1,60217733(49) × 10-19 C |
| Constante de Avogadro | NA | 6,0221367 (36) × 1023 mol-1 |
| Constante de Boltzmann | K=R/NA | 1,380658 (12) × 10-23 J K-1 |
| Constante de Faraday | F | 9,6485309 (29) × 104 C mol-1 |
| Constante de los gases | R | 8,314510 (70) × J K-1 mol-1 |
| Constante de Loschmidt | NL | 2,686763 (23) × 1025 mol-3 |
| Constante de Planck | h | 6,6260755 (40) × 10-34 J s |
| Constante de Stefan-Boltzmann | σ | 5,67051 (19) × 10-8 Wm-2 K-4 |
| Constante eléctrica | ε0 | 8,854187817 × 10-12 F m-1 |
| Constante gravitacional | G | 6,67259 (85) × 10-11 m3 Kg-1 s-2 |
| Constante magnética | μ0 | 4π × 10-7 Hm-1 |
| Masa en reposo del electrón | me | 9,1093897 (54) × 10-31 Kg |
| Masa en reposo del neutrón | mn | 1,6749286 (10) × 10-27 Kg |
| Masa en reposo del protón | mp | 1,6726231 (10) × 10-27 Kg |
| Velocidad de la luz | c | 2,99792458× 108 m s-1 |
| Constante de estructura fina | α | 2 π e2/h c |

Desde el Big Bang, cuando aparecieron las fuerzas fundamentales, también lo hicieron las constantes universales que contribuyen a que, nuestro Universo sea tal como lo conocemos y posibilitan la presencia de vida aquí en la Tierra, y posiblemente, en otros muchos planetas.
Unas pueden ser más constantes naturales que otras, pero lo cierto es que, de momento, han servido como herramientas eficaces.
La última lección importante que aprendemos de la manera en que números puros como α (alfa) definen el mundo, es el verdadero significado de que los mundos sean diferentes. El número puro que llamamos constante de estructura fina, e indicamos con α, es como decimos en el comentario siguiente, una combinación de e, c y h (el electrón, la velocidad de la luz y la constante de Planck). Inicialmente, podríamos estar tentados a pensar que un mundo en el que la velocidad de la luz fuera más lenta sería un mundo diferente. Pero sería un error. Si e, h y c cambian de modo que los valores que tienen en unidades métricas (o cualesquiera otras) fueran diferentes cuando las buscamos en nuestras tablas de constantes físicas, pero el valor de α permaneciera igual; este nuevo mundo sería observacionalmente indistinguible de nuestro mundo. Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza.

Fue Einstein el que anunció lo que se llamó principio de covariancia: que las leyes de la naturaleza deberían expresarse en una forma que pareciera la misma para todos los observadores, independientemente de dónde estuvieran situados y de cómo se estuvieran moviendo. Cuando trató de desarrollar este principio, Einstein tuvo dificultades; no encontraba la manera de expresarlo con la formulación matemática adecuada. Pidió ayuda a su amigo Marcel Grossmann, matemático, quien sabiendo de las necesidades exactas de Einstein, le envió la copia de una conferencia que dio un tal Riemann, unos sesenta años antes.
Einstein fue muy afortunado, ya que durante la última parte del siglo XIX en Alemania e Italia, matemáticos puros habían estado inmersos en el estudio profundo y detallado de todas las geometrías posibles sobre superficies curvas. Habían desarrollado un lenguaje matemático que automáticamente tenía la propiedad de que toda ecuación poseía una forma que se conservaba cuando las coordenadas que la describían se cambiaban de cualquier manera. Este lenguaje se denominaba cálculo tensorial. Tales cambios de coordenadas equivalen a preguntar qué tipo de ecuación vería alguien que se moviera de una manera diferente.

Riemann , Georg Bernhard
Einstein se quedó literalmente paralizado al leer la Conferencia de Riemann. Allí, delante de sus propios ojos tenía lo que Riemann denominaba Tensor métrico. Einstein se dio cuenta de que era exactamente lo que necesitaba para expresar de manera precisa y exacta sus ideas. Así llegó a ser posible la teoría de la relatividad general.
Einstein pudo expresar su principio de covariancia expresando sus leyes de la naturaleza como ecuaciones tensoriales, que poseían automáticamente la misma forma para todos los observadores.
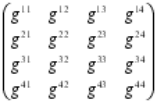
Tensor métrico de Riemann: 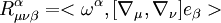
La geometría de los espacios curvos de Riemann hizo posible la relatividad general de Einstein que se pasó siete años buscando la formulación adecuada a su ideas.
Este paso de Einstein completó un movimiento espectacular en la concepción física de la naturaleza que ha sido completado en el siglo XX. Está marcado por una evolución que se aleja continuamente de cualquier visión privilegiada del mundo, sea una visión humana, basada en la Tierra, o una visión basada en patrones humanos, la naturaleza tiene sus propios patrones (el 137 es un ejemplo de ello).

El Universo es igual en todas partes
Está claro que pensar siquiera en que en nuestro universo, dependiendo de la región en la que nos encontremos, habrá distintos leyes físicas, sería pensar en un universo chapuza. Lo sensato es pensar como Einstein y creer que en cualquier parte del universo rigen las mismas leyes físicas, hasta que no se encuentre pruebas reales a favor de lo contrario, los científicos suponen con prudencia que, sea cual fueren las causas responsables de las pautas que llamamos “Leyes de la Naturaleza”, es mucho más inteligente adoptar la creencia de la igualdad física en cualquier parte de nuestro universo por muy remota que se encuentre; los elementos primordiales que lo formaron fueron siempre los mismos:
Quarks y Leptones que formaron los hadrones llamados bariones (como protones, neutrones y otros) para conformar la materia que vemos a nuestro alrededor, en los cielos y en el Universo profundo. Todo eso, grande o pequeño, está formado por la materia que está hecha de estos infinitesimales objetos ciudadanos del mundo cuántico y que se juntan por miles y cientos de miles de millones para dejarse ver en forma de mundos, de estrellas y galaxias y, ¿por qué no? también de seres vivientes racionales o no (aunque la definición de racionales no parece muy convincente).
emilio silvera
















 Totales: 75.657.702
Totales: 75.657.702 Conectados: 48
Conectados: 48