Feb
22
Los núcleos, la masa, la energía…¡La Luz!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (30)
Comments (30)
Hay veces en las que nos cuentan cosas y hechos de los que nunca hemos tenido noticias y, resultan del máximo interés. Nuestra curiosidad nos llama a desentrañar los misterios y secretos que, tanto a nuestro alrededor, como en las regiones más lejanas del Universo, puedan haber ocurrido, puedan estar sucediendo ahora, o, en el futuro pusidieran tener lugar, ya que, de alguna manera, todas ellas tienen que ver con nosotros que, de alguna manera, somos parte de la Naturaleza, del Universo y, lo que sucedió, lo que sucede y lo que sucederá… ¡Nos importa!
El saber ocupa un lugar en nuestras mentes

No podemos saber si la Humanidad como tal, estará aquí mucho tiempo más y, si con el tiempo y los cambios que se avecinan, nosotros los humanos, mutaremos hacia seres más completos y de mayor poder de adaptación al medio. Y, desde luego, nuestros descendientes, llegara un dia lejano en el futuro en el cual, habrán dejado la Tierra antes de que se convierta en Gigante Roja y calcine el Planeta y, habrán colonizado otros mundos. Para eso faltan mucho miles de millones de años. En la actualidad, solo estamos dando los inseguros primeros pasos por los alrededores de nuestro hogar, plantearnos ir mucho mas allá, es impensable. No tenemos ni la capacidad tecnológica ni la inteligencia necesaria para desarrollar los medios que se necesitan para poder desplazarnos a otros mundos lejanos que, posiblemente, estando situados en zona habitable como la misma Tierra, nos podrían dar el cobijo necesario para su colonización y hacer de ellos nuestros futuros hogares.
El futuro: Siempre será incierto
Pero, hablemos de Física

La partícula emitida por un núcleo radiactivo, por lo general lleva una considerable cantidad de energía. Y, ¿de dónde procede esa energía? Es el resultado de la conversión en energía de una pequeña parte del núcleo (E = mc2); en otras palabras, el núcleo siempre pierde un poco de masa en el acto de expeler la partícula.
Los físicos se vieron durante mucho tiempo turbados por el hecho de que, a menudo, la partícula beta emitida en una desintegración del núcleo no alberga energía suficiente para compensar la masa perdida por el núcleo. En realidad, los electrones no eran igualmente deficitarios. Emergían con un amplio espectro de energías, y el máximo (corregido por muy pocos electrones) era casi correcto, pero todos los demás no llegaban a alcanzarlo en mayor o menos grado. Las partículas alfa emitidas por un nucleido particular poseían iguales energías en cantidades inesperadas. En ese caso, ¿qué era erróneo en la emisión de partículas beta?, ¿qué había sucedido con la energía perdida?
En 1.922, Lise Maitner se hizo por primera vez esta pregunta, y hacia 1.936 Niels Bohr estaba dispuesto a abandonar el gran principio de conservación de la energía, al menos en lo concerniente a partículas subatómicas. En 1.931 Wolfgang Pauli sugirió una solución para el enigma de la energía desaparecida. Tal solución era muy simple: junto con la partícula beta del núcleo se desprendía otra, que se llevaba la energía desaparecida. Esa misteriosa segunda partícula tenía propiedades bastante extrañas; no poseía carga ni masa. Lo único que llevaba mientras se movía a la velocidad de la luz era cierta cantidad de energía. A decir verdad, aquello parecía un cuerpo ficticio creado exclusivamente para equilibrar el contraste de energías.

Habitualmente aceptamos que la física es la ciencia que estudia la estructura y propiedades de la materia y la energía, las formas de existencia de las mismas en el espacio y el tiempo, así como las leyes de rigen sus interacciones. En este definición no hay limitaciones precisas entre la naturaleza viviente e inanimada, y aunque ello no implica la reducción de todas las ciencias a la física, se deduce que las bases teóricas finales de cualquier dominio de las ciencias naturales tienen una naturaleza física.
Pero, sigamos…
Sin embargo, tan pronto como se propuso la posibilidad de su existencia, los físicos creyeron en ella ciegamente. Y esta certeza se incrementó al descubrirse el neutrón y al saberse que se desintegraba en un protón y liberaba un electrón que, como en la decadencia beta, portaba insuficientes cantidades de energía. Enrico Fermi dio a esta partícula putativa el nombre de neutrino, palabra italiana que significa “pequeño neutro”.
El neutrón dio a los físicos otra prueba palpable de la existencia del neutrino. Como ya he comentado en otra página de este trabajo, casi todas las partículas describen un movimiento rotatorio. Esta rotación se expresa, más o menos, en múltiplos de una mitad, según la dirección del giro. Ahora bien, el protón, el neutrón y el electrón tienen rotación de una mitad. Por tanto, si el neutrón con rotación de una mitad origina un protón y un electrón, cada uno con rotación de una mitad, ¿qué sucede con la ley sobre conservación del momento angular? Aquí hay algún error. El protón y el electrón totalizan una mitad con sus rotaciones (si ambas rotaciones siguen la misma dirección) o cero (si sus rotaciones son opuestas); pero sus rotaciones no pueden sumar jamás una mitad. Sin embargo, por otra parte, el neutrino viene a solventar la cuestión. Supongamos que la rotación del neutrón sea +½, y admitamos también que la rotación del protón sea +½ y la del electrón -½, para dar un resultado neto de cero. Demos ahora al neutrino una rotación de +½ y la balanza quedará desequilibrada.
+½ (n) = +½ (p) – ½ (e) + ½ (neutrino)
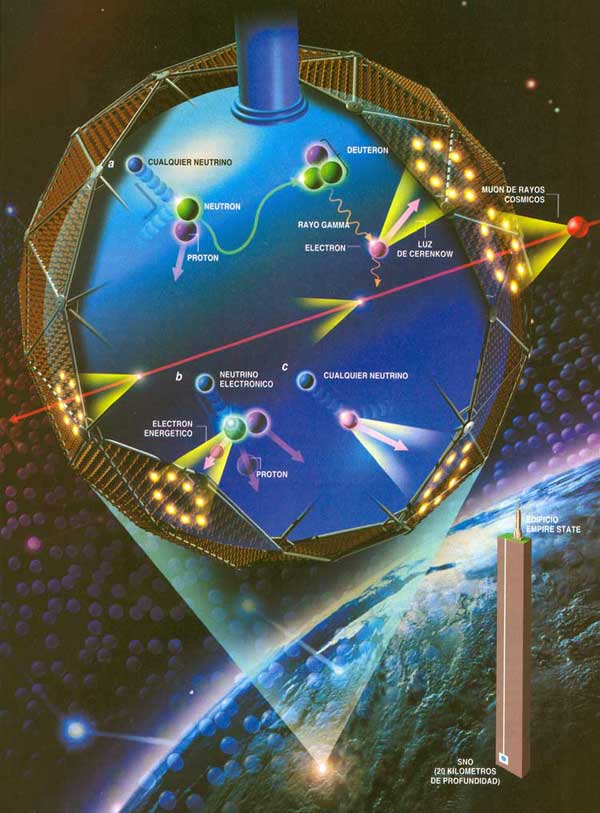
Detectando Neutrinos
En otras palabras, la existencia de neutrinos y antineutrinos debería salvar no una, sino tres, importantes leyes de conservación: la conservación de la energía, la de conservación del espín y la de conservación de partícula/antipartícula.
Pero aún queda algo por desequilibrar. Una sola partícula (el neutrón) ha formado dos partículas (el protón y el electrón), y si incluimos el neutrino, tres partículas. Parece más razonable suponer que el neutrón se convierte en dos partículas y una antipartícula. En otras palabras: lo que realmente necesitamos equilibrar no es un neutrino, sino un antineutrino.
El propio neutrino surgiría de la conversión de un protón en un neutrón. Así pues, los productos serían un neutrón (partícula), un positrón (antipartícula) y un neutrino (partícula). Esto también equilibra la balanza.

Impresionante vista de la Vía Láctea desde el Manua Kea. La Galaxia, el Universo…Todo es energía.
Es importante conservar esas leyes puesto que parece estar presentes en toda clase de relaciones nucleares que no impliques electrones o positrones, y sería muy útil si también se hallasen presentes en reacciones que incluyesen esas partículas. Las más importantes conversiones protón-neutrón son las relacionadas con las reacciones nucleares que se desarrollan en el Sol y en los astros. Por consiguiente, las estrellas emiten radiaciones rápidas de neutrinos, y se calcula que tal vez pierdan a causa de esto el 6 u 8% de su energía. Pero eso sería meternos en otra historia y, por mi parte, con la anterior explicación sólo trataba de dar una muestra del ingenio del hombre que, como habréis visto, no es poco.
Desde que puedo recordar, he sido un amante de la física. Me asombran cuestiones como la luz, su naturaleza de un conglomerado de colores, ondas y partículas, su velocidad que nos marca el límite del máximo que podemos correr en nuestro universo, y en fin, muchos otros misterios que encierra esa cosa tan cotidiana que nos rodea y lo inunda todo haciendo posible que podamos ver por donde vamos, que las plantas vivan y emitan oxígeno o que nos calentemos. Realmente, sin luz, nuestra vida no sería posible. Entonces, ¿qué es realmente la luz?

Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales grandes o muy pequeños como las galaxias o los electrones, son materia. La luz, sin embargo, se cree que es inmaterial; dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo creo que la luz es simplemente una forma de energía lumínica, una más de las diversas formas en las que puede presentarse la materia. Nosotros mismos, en última instancia, somos luz.
Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.
Cuando la luz entra en un cristal o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

¿Nos suplirán un día? Seguro que en el futuro, serán otros los que hagan experimentos con la luz y busquen su verdadera naturaleza.
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta de las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma (las dos refracciones en la misma dirección se originan porque los lados del prisma se encuentran en ángulo en vez de en forma paralela, como sería el caso de una lámina ordinaria de cristal).

Newton dedujo que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro” fantasma).
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo verde, azul y violeta, en este orden. Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa espectro o fantasma). Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades. Le surgieron y se planteó algunas inquietantes cuestiones: ¿por qué se refractaban las partículas de luz verde más que las de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbarse mutuamente, es decir, sin que se produjeran colisiones entre partículas?
Christiaan Huygens por Caspar Netscher(1671).
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar las diversas difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda más corta que la luz azul; ésta, más corta que la verde, y así sucesivamente.

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna (las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades).
Pero la teoría de Huyghens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos, ni por qué proyectaban sombras recortadas, ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las estrellas? ¿Cuál era esa mecánica ondulatoria?

Con el éxito de Newton de su ley de la Gravitación Universal, no es extraño que afirmara de forma tajante que la luz es corpuscular. Newton se opuso violentamente a la naturaleza ondulatoria de la luz, ya que no veía cómo se podía explicar con ella la propagación rectilínea de la misma. Por otro lado estaba Christian Huygens, 13 años mayor que Newton que defendía la naturaleza ondulatoria con algunas ventajas.

Ambas teorías explicaban perfectamente la reflexión y refracción de la luz. Pero diferían en una cosa. La teoría corpuscular afirmaba que las partículas de luz se acelerarían al pasar por un material de mayor densidad óptica y las ondas a menor. Esto no era comprobable por aquella época. Debido a la influencia de Newton y a la poca habilidad de Huygens para desarrollarla matemáticamente, la teoría ondulatoria quedó descartada durante un siglo.
Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular de Newton fue, con mucho, la más popular, en parte porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico inglés, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos; si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras; pareció incluso que en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.
Sería fácil explicarlo mediante la teoría ondulatoria; la banda luminosa representaba el refuerzo prestado por las ondas de un rayo a las ondas del otro, dicho de otra manera, entraban “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en los que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.

Considerando la anchura de las bandas y la distancia entre los dos orificios por lo que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o de los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Ángstrom; esta unidad, denominada igualmente Ángstrom (Å) en honor a su autor, es la cienmillonésima parte de un centímetro. Así pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Å, y la de la luz violeta a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si este no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior al de una onda luminosa, y por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de onda luminosa (por ejemplo, los virus y otras partículas subatómicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.
Un físico francés, Agustin-Jean Fresnel, fue quien demostró por vez primera en 1.818 que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de difracción” actúan como una serie de minúsculos obstáculos, que se refuerzan entre sí. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.

La mano del Universo juguetea con unos puntos luminosos que quieren llegar a ser cegadores…Son nuestras Mentes, productos de la evolución del Universo que, a partir de la materia inerte, ha podido alcanzar el estadio bio-químico de la consciencia y, al ser conscientes, hemos podido descubrir que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso, los rayos espectrales. El físico americano Henry Augustus Rowland ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscópio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.
No sólo se aceptó la existencia de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalcanzable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.

Tubo de descarga lleno de kriptón puro
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuales aportaba una raya cuya longitud de inda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de la longitud. Entonces se reestableció la longitud del metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumentó mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
emilio silvera
















 Totales: 83.359.021
Totales: 83.359.021 Conectados: 70
Conectados: 70

























el 22 de febrero del 2018 a las 16:59
Pregunta acerca de la velocidad de la luz, resulta que su valor máximo es 300.000km/s.en el vacío. E inferior dependiendo del medio.ok.
Resulta nada puede circular a mayor velocidad, ya que se requiriera una energía inmensa, Y a medida que nos fuéramos acercando, dicha partícula en vez de aumentar su velocidad, aumentaría más su masa, necesitando mayor energia y así sucesivamente. Osea un imposible.
Pregunta: Acerca de su valor. (c) ¿Que determina que su valor es el que tiene y no otro valor distinto?
En el caso de la constante de estructura fina su valor viene de la relación entre distintos componentes, como carga de electrón, constante de planck,.velocidad de la luz, etc.
Repito la pregunta: En el caso de (c), cuáles son esos componentes, que hacen que su valor sea 300.000 km/s. Y no otro valor distinto.
No me sirve el ejemplo de: calcular la velocidad de distintos vehículos, si a tal, si b tal, si c tal. Esa no es la pregunta. Habló acerca del valor que tiene (c).ok
Gracias.
el 22 de febrero del 2018 a las 20:47
Hola muchachada.
Hola Pedro.
Entiendo que en el caso de la constante de estructura fina, se trata de un número puro, adimensional, independiente del sistema de unidades usado, como otras constantes como π (Pi) o como el número “Áureo”.
En el caso de “c”, se trata de una velocidad concreta, objetiva, que no depende de otros valores, que ha ido variando con la edad del Universo y cuya medición se ha ido perfeccionando con los avances de la Ciencia.
Aquí puedes leer un interesante y ameno resumen de la historia de esa medición:
https://es.wikipedia.org/wiki/Velocidad_de_la_luz#Medici%C3%B3n_de_la_velocidad_de_la_luz
Saludos cordiales para tod@s.
el 23 de febrero del 2018 a las 5:15
Todo el meollo de la cuestión está en la carencia de masa de los fotones.
Saludos.
el 22 de febrero del 2018 a las 23:19
Respecto al valor de (C), supongo que será el que es simplemente por haber sido comprobado experimentalmente.
Otro problema subyacente en la pregunta de Pedro podría ser por qué en la famosa fórmula ” e = mc2″ se aplique justamente la masa por la velocidad de la luz al cuadrado para determinar la energía de un cuerpo.
Como simple aficionado, solo puedo dar mi parecer; y es que precisamente la velocidad de la luz la efectúa el fotón, una partícula que carece de masa en reposo, y que es el más claro exponente de la dualidad onda-partícula, digamos que se encuentra entre la energía y la materia. Y a través de sus cuantos expresa la misma dualidad entre la masa y la energía, por lo que en su inevitable movimiento a 300.000k/s, convierte esa velocidad en unidad de medida, por otra parte ,y posiblemente, única referencia de medida.
A ver que opinan los entendidos.
el 23 de febrero del 2018 a las 5:16
Como de costumbre, amigo Kike… ¡Has dado en la diana! La carencia de masa de los fotones.
el 22 de febrero del 2018 a las 23:26
Incidiendo en el comentario anterior; si Pedro se refiere al motivo por el que el fotón vaya a esa velocidad en el vacío y no a otra, supongo que será precisamente por carecer de masa al estar en movimiento, y por tanto, porque no se puede ir más rápido; siendo este uno de los motivos por los que ese límite se considera una ley universal bien implantada y comprobada.
Para mi, la luz es uno de los más grandes misterios del universo junto al agua, ya que ambos tienen peculiaridades casi infinitas y nada bien conocidas todavía.
el 23 de febrero del 2018 a las 10:38
Me gusta la respuesta, osea falta de masa de dichos fotones. No obstante con cero masa, difícil resolución de acuaciones salvo sumar o restar. Tengo que mirar masa en reposo y nada nula.
el 23 de febrero del 2018 a las 11:09
En cualquier sitio que quieras mirar, te dirán:
“El fotón tiene una masa invariante cero, y viaja en el vacío con una velocidad constante c {\displaystyle c} . Como todos los cuantos, el fotón presenta tanto propiedades corpusculares como ondulatorias (“dualidad onda-corpúsculo“). Se comporta como una onda en fenómenos como la refracción que tiene lugar en una lente, o en la cancelación por interferencia destructiva de ondas reflejadas; sin embargo, se comporta como una partícula cuando interactúa con la materia para transferir una cantidad fija de energía, que viene dada por la expresión:
donde h es la constante de Planck, c es la velocidad de la luz, λ {\displaystyle \lambda } es la longitud de onda y ν {\displaystyle \nu } la frecuencia de la onda. Esto difiere de lo que ocurre con las ondas clásicas, que pueden ganar o perder cantidades arbitrarias de energía. Para la luz visible, la energía portada por un fotón es de alrededor de 4×10–19 julios; esta energía es suficiente para excitar las células oculares fotosensibles y dar lugar a la visión.”
Si nos fijamos en los neutrinos que tienen una masa mínima, no pueden alcanzar la velocidad de la luz, es la falta de masa la que permite tal velocidad límite en nuestro Universo.
el 23 de febrero del 2018 a las 14:35
En la famosa ecuación de Einstein (y en cualquier otra), m y e son variables; c no. Es un valor absoluto.
Un fotón en reposo es una contradicción, un imposible. Si hay “que mirar masa en reposo y nada nula”, entonces creo que no deberíamos hablar de fotones ni de c.
Saludos.
el 23 de febrero del 2018 a las 11:26
Entre 0 y 1 todo un misterio , entre 0 y 0,1 todo un abismo. ,Y ente +1 y -1 ya ni te cuento.
el 23 de febrero del 2018 a las 23:14
El fotón no tiene masa La característica intrínseca de su “masa invariable” se cree que es estrictamente cero, con base en la experimentación y consideraciones teóricas. Esto respecto de la definición estándar de masa entre los físicos. No obstante, algunas explicaciones científicas populares han asignado al fotón una “masa relativista” definida como E/c2, donde E representa la energía de la partícula.
A esto me refirió, un cuanto o fotón tiene que tener masa por pequeña quesea. Si no en ecuaciones sus resultados son imposibles.
el 24 de febrero del 2018 a las 6:27
Amigo Pedro, ya saves, la masa y la energía son equivalentes, un aspecto de la misma cosa.
el 24 de febrero del 2018 a las 6:28
“… ya sabes…”
el 25 de febrero del 2018 a las 16:56
Por cierto acerca de la observación, en su día de Kike, muy buena por cierto.e=mc2, efectivamente si viene a indicar que energía y masa son lo mismo,osea equivalentes. Nada que objetar. No obstante como ecuación desde el punto de vista matemático fantástica todo normal. Pero si resulta que nada puede superar c, Entonces que pinta el exponente 2 si ningun hecho físico lo puede refrendar .
el 26 de febrero del 2018 a las 12:58
La ecuación de la energía de la de cuadridimensión, es decir el cuadrivector (En el espacio) nos da la pauta.
En el desarrollo en el espacio de un elemento, se considera un impulso p =mv, que para c es mc. Desarrollado geométricamente. Sin embargo este solo término no dice gran cosa si no se considera el segundo, donde ya entra la energía (1/2 mc^2) tambien cuadrático. Por qué esta velocidad cuadrática. Porque la onda no es lineal si no que va ocupando un espacio o volumen transversal, también a la velocidad c. Como dicha energia no es lineal sino “extendida” el resultado qued como la extensión a un cuadrado, es decir c·c =c^2.
La interpretación del cuadrivector puede hacerse en consideración solo de p=impulso matemático, sin más, donde milagrosamente no se considera masa alguna, o en toda su significado, de donde surge el concepto de onda partícula. Lo que se expresa segun:
h·f = mc^2
el 26 de febrero del 2018 a las 1:23
Hola muchachada.
Hola Pedro.
Desconozco cómo llega Einstein a la fórmula; seguramente tras largos y complejos cálculos; es más bien tarea de matemáticos. Pero no hay ya duda alguna de su certeza. Ha sido refrendada empíricamente en incontables ocasiones. Las más famosas, tristemente, son las bombas atómicas, cuya potencia se prevé con exactitud. O los reactores nucleares.
Saludos cordiales para todos.
el 26 de febrero del 2018 a las 6:43
Demostrado una y mil veces
el 26 de febrero del 2018 a las 10:09
Haber si me explico :Sabemos de las consecuencias de dicha fórmula.ok bombas, el incremento de masa de los propios muones, en los aceleradores, etc. Cuando hablo de que no hay ningún hecho físico que lo pueda refrendar. Me estoy refiriendo a c al cuadrado de hay mi perplejidad. Como en una ecuación que sus componentes son reflejos de parámetros de hechos físicos. Uno de sus componentes es una quimera. Ya que nada viaja a más de c. Espero que ahora haya quedado más claro. Un saludo para todos.
el 26 de febrero del 2018 a las 10:31
El periodista estadounidense WALTER Isaacson, nos dejó una didáctica explicación de la famosa fórmula:
el 26 de febrero del 2018 a las 17:15
Hola muchachada.
La explicación de Fandila podría provocar una repregunta: ¿porqué al cuadrado y no al cubo?… ya que si bien “dicha energía no es lineal sino extendida” la dirección de los fotones es tridimensional. Por lo que insisto en tomar la comprobación empírica de la fórmula final como la prueba incontrovertible de su certeza, ya que creo que (tal vez salvo Fandila y Emilio) ninguno de los participantes en esta conversación estamos en condiciones de seguir los complejos cálculos previos que llevaron a Einstein a su famosa formulación.
¿Porqué al cuadrado?; ¿porqué c = 300000k/s y no otra velocidad?; ¿porqué Júpiter tiene al menos 69 satélites y no 60?. Aunque desconozcamos las razones últimas, conocemos fehacientemente (objetivamente) algunas respuestas.
Saludos cordiales.
el 26 de febrero del 2018 a las 19:07
Haber si aclaro el entuerto, y pido mis disculpas ok.
el 26 de febrero del 2018 a las 22:00
Pedro.
Aquí parece estar aclarada tu consulta:
https://es.wikipedia.org/wiki/Equivalencia_entre_masa_y_energ%C3%ADa#Interpretaci%C3%B3n_geom%C3%A9trica_espacio-temporal_de_la_ecuaci%C3%B3n
Yo no entiendo esas ecuaciones, pero confío que son correctas. No creo que incluya miembros arbitrarios ni quimeras de ningún tipo. Si tú puedes interpretarlas y resolverlas, seguramente tendrás tu respuesta.
Saludos cordiales.
el 27 de febrero del 2018 a las 11:40
En una onda normal el avance no solo se realiza longitudinalmente, sino que la misma velocidad de avance tambien la posee en la scilación. Por tanto la energía de un supuesto elemento lo hace en dos direcciones: longitudinal de avance a c y transversal también de avance c. La resultante, uadrivector (Por extenderse en las cuatro dimensiones del espacio tiempo), nos da resultados cuadráticos (al cuadrado) y a la cuarta. Luego vine su interpretación.
Desarrollando las energías cinéticas se obtiene: 2· (las dos direcciones) · 1/2 mc^2 = mc^2
Desconozco que fue antes para Einstein si el cuadrivector o la intuición primera con su relatividad, que luego se confirmara
el 26 de febrero del 2018 a las 17:22
De todas formas, lo que dice Pedro tiene sentido; porque una fórmula se supone que debe ser exacta; por lo que el cálculo de que la masa sea equivalente a la de la velocidad de la luz al cuadradado, o se debe a un dato aproximativo (Puesto que Einstein no pudo comprobarlo experimentalmente), o lo sacó a base de matemáticas (como comenta Nelson).
Por ello, y a falta de que alguien lo sepa y nos lo comente, esa correlación exacta entre masa y energía hubo de sacarse a costa de las matemáticas; y si eso fue así; ¿De donde se sacaron esas matemáticas en 19000?
Por lo visto, en la formulación matemática de la Teoría General de la Relatividad, y puesto que Einstein no era demasiado experto en matemáticas, fue ayudado por su amigo y excelente matemático Planck; y dado que Planck fue el precursor de los “cuantos”, quizás, al individualizar y tomar medida a la luz se pudo determinar matemáticamente su equivalencia con la masa.
—O tal vez no—
el 26 de febrero del 2018 a las 18:19
Ojo con la confusión sobre la capacidad en matemáticas de Einstein.
Leo en Wikipedia:
“El colegio no lo motivaba, y aunque era excelente en matemáticas y física, no se interesaba por las demás asignaturas. A los quince años, sin tutor ni guía, emprendió el estudio del cálculo infinitesimal. La idea, claramente infundada, de que era un mal estudiante proviene de los primeros biógrafos que escribieron sobre Einstein, que confundieron el sistema de calificación escolar de Suiza (un 6 en Suiza es la mejor calificación) con el alemán (un 6 es la peor nota).18 En este “Erziehungsrat” aparece con nota 6 en todas las asignaturas: Álgebra, Física, Geometría, Geometría Analítica y Trigonometría.”
Saludotes.
el 26 de febrero del 2018 a las 22:43
Seguro que era un matemático excelente; de hecho todos los físicos lo son.
Pero en su biografía recuerdo haber leído que su amigo Planck le ayudó bastante en diferentes fórmulas (Las dominaba más); e incluso hasta su primera esposa (Mileva?), que también era una gran matemática, le ayudó bastante; tanto que al parecer Einstein llegó a temer que le robara sus ideas, y según algunas leyendas llegó a guardar sus trabajos con claves para que ni su esposa las pudiera copiar.(Como científico habrá sido de lo mejor, pero como esposo y padre de familia fue un verdadero desastre).
Saludos Nelson.
el 27 de febrero del 2018 a las 5:18
Simplemente no era buen profesor de matemáticas, el transmitirla le era difícil, se le iban los pensamientos de una a otra cosa y los estudiantes se hacían un lío con sus explicacaciones. Por lo demás, se defendía bastante bien en matem´çaticas sin llegar a Hilbert o Tiemann.
el 26 de febrero del 2018 a las 17:29
En mi comentario anterior no había leído el último de Fandila (De todas formas aunque lo hubiera leído sería igual, porque no entiendo nada….)
“Cuadrivectores, cuadridimensiones…..”eso que é lo que é?”
Paisano Fandila, eres una caja de sorpresas; cada día me asombran más tus conocimientos.
el 26 de febrero del 2018 a las 17:51
Já, já, já,…. Cuadritensores, cuadrimomentum…… Por decía antes que no es para algunos de nosotros… No te puedo ayudar en nada pero acá hay algo de eso: https://es.wikipedia.org/wiki/Teor%C3%ADa_de_la_relatividad#Magnitudes_f%C3%ADsicas
Un abrazo.
el 27 de febrero del 2018 a las 5:19
Amigo Kike, no olvides que el amigo Fandila, en Física, está bien preparado.