Abr
1
¿Cuándo sabremos comprender lo que estamos viendo?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Los ácaros que podemos ver con el microscopio electrónico permite observar sus movimientos: los descubre casi siempre en grupos, semejando divisiones blindadas que avanzan en formación por paisajes sinuosos y áridos, como desiertos diminutos. Es decir, nos tenemos que valer de poderosos aparatos electrónicos para poder constatar esa realidad.
Nuestra realidad es que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.
Esas creencias que nos han metido en la mente desde niño son muy poderosas y, despojarnos de ellas, no es cosa fácil. Nos condicionan durante toda la vida y se convierten en ese muro que no nos deja “ver” más allá. En cada sitio y en cada liugar, en cada parte del mundo, tienen sus propias creencias y costumbres y, arrojarlas de nosotros…


Sí, ambas imágenes son del mismo Tiempo pero, de diferentes lugares y costumbres
Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarmos más y más a esa realidad que presentimos, y, para ello observamos y experimentamos, nos fijamos en cómo funciona la Naturaleza a nuestro alrededor y, según la entendemos, tratamos de reflejar, en esos modelos, lo que realmente ocurre. Sin embargo, nuestras perscepciones pueden estar viciadas y, los resultados, no ajustarse a esa realidad que perseguimos.

Cada mente esconde su propio mundo. Chica rodeada de fantasía

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.
Soñando me llegó la idea maravillosa
Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.
Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.
En esta aproximación muestra la prueba de texturizado del modelo 3D finalmente seleccionado. El personaje que aparece a la par, es la persona real. y la que aparece sin pelo es el modelo 3d renderizado. No siempre la realidad está clara ante nuestra vista.
Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:
1 – 1/3 + 1/5 – 1/7 ….
Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente, se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.


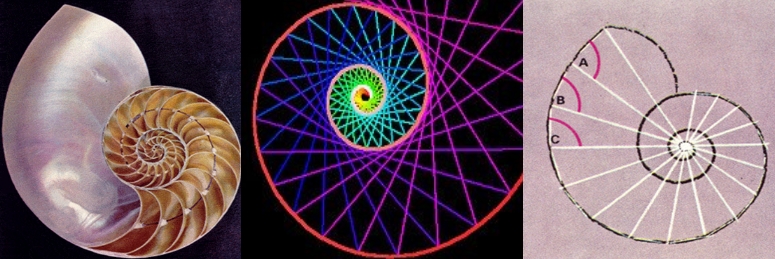
Hacemos una parada aquí para dejar una nota que nos dice que independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y entre otros temas. Si hablamos de “Pi” mos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN, el efecto mariposa y la Torah, entre otras muchísimas cosas que se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes representado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.
No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.
El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.
Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.
Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.
¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.



3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th
Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejemplo:
Roger Penrose dedicó bastante más tinta en defender los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.
Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

¿Es la verdad inalcanzable?
Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.
Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitir nuestros múltiples u dispares pensamientos:
- Los Computadores nunca podrán reemplazar la estupidez humana.
- El hombre nace ignorante, la educación lo idiotiza.
- Una persona inteligente resuelve problemas, el genio los evita.
- Las mujeres consideran que guardar un secreto, es no revelar la fuente.
- Todas las mujeres tienen algo bonito… así sea una prima lejana.
- La felicidad es una lata de atún, pero con el abrelatas un poco distante.
- El único animal que no resiste aplausos es el mosquito.
- El amor está en el cerebro, no en el corazón.
- Definición de nostalgia “es la alegría de estar triste”.
- “Mi segundo órgano favorito es el cerebro”. Woody Allen.
Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

¿En nuestras Mentes? ¡Cien mil millones de neuronas! Como estrellas en la Vía Láctea
Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.
Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…
O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!
Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?
Todo eso está bien pero, ¿Quien es PI?

Bueno, Pi y Fi encierran todo un mundo de misterios


Abr
1
Nos adentramos en la Física con el Tiempo de Planck
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
Tiempo de Planck
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por ![]() , donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
, donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
El valor del tiempo del Planck es del orden de 10-44 segundos. En la cosmología del Big Bang, hasta un tiempo Tp después del instante inicial, es necesaria usar una teoría cuántica de la gravedad para describir la evolución del Universo.
Expresado en números corrientes que todos podamos entender, su valor 0,000.000.000.000.000.000.000.000.000.000.000.000.000.0010 de 1 segundo que es el tiempo que necesita el fotón para recorrer la longitud de Planck, de 10-35 metros (veinte ordenes de magnitud menor que el tamaño del protón de 10-15 metros). El límite de Planck es ![]()
Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.
Abr
1
Lo que no sabemos: ¿Cómo se formaron las galaxias?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)

Tarde de domingo en la isla de la Grande Jatte – Georges Pierre Seurat, 1884
El Art Institute de Chicago tiene una de las mejores colecciones del mundo de pintura de finales del siglo XIX francés, reúnida durante la época en que la ciudad era realmente “un matarife para el mundo, jugando con los ferrocarriles de una nación”. Una de las obras más populares es un gran lienzo de George Seurat. Su título formal es La Grande Jatte, pero se conoce coloquialmente como Domingo por la tarde en el parque.
Muestra a un grupo de parisinos paseando por un parque junto al Sena. La pinturá incluso inspiró una revista en Broadway llamada Domingo el el parque con George. Saurat utilizó una técnica pictórica que era bastante poco usual en su época. En lugar del pasar el pincel sobre el lienzo en la forma habitual, tocaba el lienzo sólo con la punta.
El resultasdo es una pintura formada por un gran número de pequeñas motas de color. Este estilo de Pintura se llama puntillismo. A causa de esa técnica, el mirar esa pintura resulta una experiencia extraña. Desde lejos se ve lo que pretendía el pintor, la escena de un parque con figuras en él. Sin embargo, si nos acercamos mucho, la escena desaparece y lo que se verá será una colección de puntos de color sobre un lienzo. La uniformidad, que es aparente cuando miramos a la “imagen grande”, oculta la apariencia real de lo que allí está presente.
¿Nos pasará a nosotros otro tanto cuando miramos el Universo? Seguro que sí, ya que, si tuviéramos las narices pegadas a cualquiera de esas galaxias, no veríamos nada excepto un borrón de luz y de color. ¡Qué extraño es el mundo que nos rodea y cuánto nos cueta comprenderlo!

La pintura de Saurat proporciona una útil analogía para una de las ideas favoritas de los astrónomos acerca de la estructura del Universo: la idea de que si miramos a una escala bastante grande, encontramos que el universo es uniforme y homogéneo. A partir de Einstein los comólogos de “punta” han supuesto que esta afirmación es cierta. Claro que, una cosa es lo que se supone y otra muy distinta lo que en realidad pasó.
Las galaxias, por ejemplo, no pudieon comenzar a formarse hasta después de que radiación y materia se desparejan y otra solución que se sugiere sola, el empujón al colapso gravitatorio mediante concentraciones de masa o cualquier otro procedimiento físico, tal como la turbulencia en las nubes de gas después de la formación de los átomos. Pero ¡ay!, esta línea de argumentación nos lleva hasta una tercera reconsideración del problema en el que finalizamos aceptando que, las turbulencias tampoco sirven.

El “impulso a través de turbulencia” es una idea simple, cuyas primeras versiones fueron aireadas allá por los años 50. El postulado es este: cualquier proceso tan violento y caótico como las primeras etapas del Big Bang no sería como un río profundo y plácido, sino como una corriente de montaña, llena de espumas y turbulencias.
En este flujo caótico podemos esperar encontrar remolinos, vórtices de gas. En esta teoría, un remolino es en efecto una concentración de masa del tipo Jeans, presionando sobre la materia que le rodea a causa de la atracción gravitatoria. Si el remolino es del tamaño necesario, puede reunir una masa del tamaño de una galaxia antes de que tenga una posibilidad de disiparse. Para entonces esa masa sería suficientemente grande, de forma que se mantendría unida por la fuerza de la gravedad cuando pase el remolino.
Está bien, pero existen algunas dificultades. En primer lugar, un remolino que se forma antes de la marca de los 500.000 años es todavía una concentración de masa, y como cualquier otra concentración de masa será destruída por la presión de la radiación. Por consiguiente, los turbulentos remolinos que sirven como núcleos de concentración para las galaxias deben acceder a la existencia después de la aparición de los átomos.

Galaxia en proceso de formación. A pesar de la enorme técnica y sofisticación de los aparatos con que contamos para la observación del cosmos, no se ha podido encontrar ninguna a protogalaxia cercana, lo cual indica que todas o la mayoría de las galaxias se formaron hace mucho tiempo.
Lo que esto significa es que los remolinos que se forman justo después de la congelación atómica son los que más probablemente conducirán a las galaxias, porque son los que tienen más tiempo para recoger materia. Si estos remolinos son del tamaño necesario, podrían realmente producir galaxias como las que podemos ver ahí arriba. Sólo tendríamos que suponer que hubiera remolinos del tamaño de galaxias (o próximos a ellas) presentes en el momento de la congelación.
Con todo, la teoría plantea un extraño tema filosófico. Podemos mirar las galaxias visibles, extrapolar hacia atrás en el tiempo y proponer un conjunto de turbulentos remolinos que las produzcan. Esto no resuelve el problema, sólo plantea la vieja cuestión de otro modo, retrocediendo una muesca. En lugar de preguntas: “¿Por qué las galaxias son como son?”, preguntamos “¿Por qué eran los remolinos como eran?” Y, seguimos sin avanzar en el problema de saber como se formaron las galaxias.
Tampoco las galaxias han tenido tiempo para formar cúmulos, y, sin embargo, ahí están. ¿Qué sabemos de los enigmas del Universo? En realidad, vamos sabiendo algo pero, lo cierto es que, son muchas más las preguntas que las respuestas.
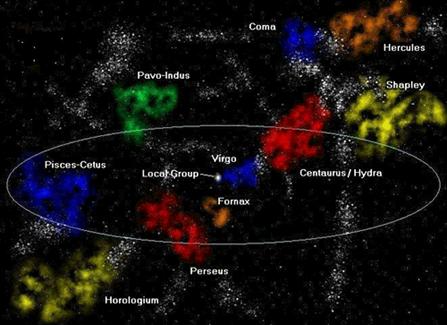
Aquí podemos contemplar el hermoso cúmulo de galaxias de Hydra
Miramos la bella imagen y vemos como dos brillantes y supermasivas estrellas destacan en el primer plano, pertenecen a la Vía Láctea, y están más cerca a nosotros. Más allá, lejos en el fondo, relucen las galaxias del cúmulo que, en el centro exhiben unas predominantes galaxias de más de 150.000 años-luz de diámetro, dos son elípticas de color amarillo (NGC 3311 y NGC 3309) la Azulada, es la espiral NGC 3312 y, justo por encima de la izquierda de NGC 3312 aparece una misteriosa pareja de galaxias superpuestas que están catalogadas como NGC 3314.
Estas imágenes, cuando se conmtemplan por personas no expertas, pueden también llevar al engaño. Por ejemplo, mientras que las estrellas del primer plano se encuentran a cientos de años-luz de distnacia, el cúmulo de galaxias de Hydra está a más de 100 millones de años-luz. Es una de los tres grandes cúmulos que hay dentro de los 200 millones de años-luz de la Vía Láctea. También es conocido como Abell 1060. En nuestro Universo, las galaxias están gravitacionalmente unidad en cúmulos y, a su vez, estos cúmulos en supercúmulos mucho mayores de muchos miles o cientos de miles de galaxias. La Imagen tiene un diámetro de cera del millón y medio de años-luz.

La gravedad es la gran fuerza estabilizadora del universo. Nunca lo abandona del todo; siempre está actuando, tratando de unir pedazos de materia. En cierto sentido, la historia entera del universo se puede pensar como un último y fútil intento de superar la gravedad. Sería asombroso, dada la naturaleza universal de la fuerza gravitatoria, que no hubiera desempeñado un papel importante en la formación de las galaxias.
Supongamos que el universo ha comenzado como una colección de materia uniformemente emplastada, en la que ninguna parte tenía mayor concentración de materia que otra. En esta situación se podría esperar se que la fuerza de la gravedad tuviera que actuar para unir todo lo que hay en el universo en un imposible sol central. Claro que, una cosa es pensarlo y otra muy distinta es la realidad.
El problema es que en cualquier colección de materia, por uniformemente distribuida que esté, habrá ligeras concentraciones en alguna parte. Incluso, aunque tengamos que descender al nivel microscópico para verlo, el movimiento aleatorio de los átomos resultará al final en un estado de la cuestión en el que hay un pequeño exceso de átomos en algunos puntos y un pequeño déficit en otros.
![[lefevre_06.jpg]](http://2.bp.blogspot.com/_m5Bv_OGYCMM/R-vE6txC2QI/AAAAAAAAAfI/A3A5YTC2Y1w/s1600/lefevre_06.jpg)
No es difícil visualizar lo que pasa a continuación. En un momento dado, el pequeño extra de materia se acumula en alguna parte, bien por causa del movimiento atómico o por alguna otra razón. Debido al momentáneo exceso de materia en ese punto, la fuerza gravitatoria ejercida por los puntos de alrededor. Por consiguiente entrará más masa en el área en que tuvo lugar la concentración original. Con más masa, la concentración puede ejercer todavía más fuerza gravitatoria y atraer todavía más materia hacia ella. No importa lo equitativa que fuera la distribución inicial, una vez que se ha formado la más pequeña concentración, la masa uniforme se romperá en pequeños pedazos cada uno formado alrededor de la concentración original de masa. Esta inestabilidad inherente a una masa de materia fue señalada por primera vez en los años veinte por el astrofísico británico sir James Jeans.
A primera vista parece un rayo de esperanza. El universo debe romperse en pequeñas unidades de masa, y con suerte, estas unidades se convertirían en galaxias. Incluso resulta que, aunque sólo hemos hablado de un universo, el resultado de Jeans sigue siendo verdad si hay la expansión de Hubble. Pero el problema no es tan sencillo. La misma teoría que nos dice que una distribución uniforme de materia es inestable frente a la rotura de pequeños pedazos, también nos dice cuánto tardará el proceso de rotura.
(Lo que mostró realmente Jeans fue que una masa en gravitación es inestable para la rotura en piezas de cierto tamaño. Si una masa es más pequeña que el pedazo más pequeño en el que puede ser dividida, la masa será estable. En otro caso, se romperá. Esta prueba se conoce como el criterio de Jeans para los expertos tiene una bien conocida fórmula, la longitud de Jeans).

La cuestión viene a ser: ¿pueden actuar las fuerzas gravitatorias con suficiente rapidez después que ha tenido lugar el desparejamiento, para reunir la materia en grupos del tamaño de una galaxia, antes de que la expansión de Hubble ponga todo fuera del alcance? Una de las grandes conmociones para la comunidad astronómica de los años treinta fue que la respuesta a esta pregunta fue un rotundo “¡NO!” Lo que parecía ser el mecanismo más probable para la formación de galaxias –el mecanismo de inestabilidad gravitatoria que acabamos de describir- no funcionará en un universo en expansión.
Quizá este hecho fue lo que condujo a Jeans, al final de su vida, a proponer un universo en el que la materia se iba creando continuamente en los vacíos que dejaba la expansión galáctica. En esta visión, la formación de galaxias es un proceso continuo, no confinado a ningún tiempo particular de la historia del universo. Esta teoría de Jeans que, al final se clasificó como universo estacionario, sería abandonada después de la acumulación de pruebas muy convincentes a favor del big bang.


La idea del universo estacionario fue un modelo cosmológico desarrollado en 1948 por Herman Bondi, Thomas Gold y Fred Hoyle como una alternativa a la teoría del Big Bang que, finalmente, prevalecería como la teoría más probable y la que más se acercaba a la obervación del espacio interestelar y que vino a confirmar la radiación de fondo cósmico como la huella dejada por aquella explosión primera.
Todo lo relacionado con la formación de las galaxias resulta muy enigmático y para los entendidos también, ya que, a ciencia cierta, como se pudieron formar… Nadie lo sabe pero, las conjeturas abundan…
Se cree que unos 10.000 años después del Big Bang la temperatura había descendido a unos 100.000 grados centígrados y se formaron los primeros átomos de hidrógeno.
Después de formase los átomos, la situación habría sido marcadamente diferente. El hecho clave aquí es que la radiación no interacciona tan fuertemente con los átomos como con las partículas cargadas en un plasma. Podéis consultar la propia memoria para ver que esta afirmación es cierta. Si habéis estado en la cima de una montaña o de un edificio alto y habéis mirado desde allí al paisaje circundante, probablemente han podido ver lindes, por ejemplo, hasta unos cincuenta o quizá cien km de distancia. En algunos lugares, como las cimas de las montañas que se elevan en el aire límpido del norte de España, pueden ver incluso más lejos.
Pero antes de que vean esas lindes, es necesario que la luz viaje desde el objeto visto hasta su ojo. La simple experiencia de ver a lo lejos, por tanto, nos dice que la luz puede viajar por el aire largas distancias sin ser dispersada o distorsionada. Esto no puede suceder en un plasma. Que suceda en el aire, que está hecho de átomos y moléculas, muestra que la interacción de la luz con esas dos formas de materia debe ser muy diferente.
Así que en el universo inicial, la secuencia de los acontecimientos debe haber sido algo así. Hasta unos 100 000 años la materia estaba en forma de plasma y no se podían haber formado objetos del tamaño de una galaxia. A los 200 000 años, los átomos comenzaron a aparecer y la interacción de la luz con la materia comenzó a debilitarse. La formación de los átomos no tuvo lugar de golpe, sino que continuó hasta la cota del millón de años. Entre esos dos momentos, el maquillaje del universo viró desde el plasma a los átomos, y cuando terminó la transición quedaban pocas partículas cargadas libres. La forma dominante de la materia era el
En algún momento durante de la formación de los átomos, la fuerza de la interacción entre la materia y radiación disminuyó hasta el punto en el que la radiación ya no se quedara atrapada dentro del plasma. La radiación circulaba libremente y, desde ese momento en adelante, tuvo poco efecto sobre el proceso de formación de los átomos, la radiación se desparejó la de la materia.
Aunque el desparejamiento fue gradual, me gustaría hacer una referencia ocasional al proceso. Hablaré de él como si hubiera ocurrido hacia la cota de los 500 000 años, pues éste es un número redondo a medio camino de la congelación de los átomos. Esto es simplemente para abreviar; no quiero dar entender que el universo fuera opaco hasta 500 000 años más un segundo.
He encontrado una analogía muy útil para visualizar el proceso de desparejamiento. Cuando os tomeis una bebida, como té helado servida en un vaso alto, observen lo que sucede si remueven el azúcar. Al principio, la bebida se vuelve turbia, porque el azúcar está en forma de terrones relativamente grandes y los terrones grandes dispersan la luz con eficacia. Saben que la dispersión es eficaz porque la luz no puede atravesar todo el vaso, sino que es dispersada. Esta luz dispersa es la que da al té su apariencia turbia. En este estado, el té es análogo al universo antes de la formación de los átomos, cuando la radiación estaba interaccionando con el plasma. Tras unos pocos momentos, el té se vuelve repentinamente transparente de nuevo. Lo que ha sucedido es que el azúcar se ha disuelto y ahora existe en forma de moléculas que interaccionan débilmente con la luz. La luz pasa ahora a través del té sin ser dispersada y la niebla ha desaparecido. Este cambio de turbio a transparente en el té se parece a lo que sucedió en el universo cuando se formaron los átomos. El universo se volvió transparente al despejarse la radiación, y no quedaba nada que contrarrestase la fuerza de la gravedad cohesionando la materia.
Así, la interacción de la radiación y la materia impide el comienzo de procesos que pudieran conducir a las galaxias antes de que el universo tuviera 500 000 años de edad. Esto resulta ser un problema importante, a causa de la lógica que nos dice que las galaxias no tuvieron tiempo de formarse.
Todo esto de las Galaxias siempre me ha planteado muchas dudas pués, lógicamente, las galaxias no pudieron haberse formado antes que los átomos. Podemos pensar en el Universo durante las primeras etapas de la expansión de Huble como formado por dos constituyentes: materia y radiación. La materia sufrió una serie de congelaciones al construir gradualmente estructuras más y más complejas. A medida que tienen lugar esos cambios en la forma de la materia, la manera en que interaccionan materia y radiación cambia radicalmente. Esto, a su vez, desempeña un papel fundamental en la formación de galaxias.
Físicos rusos, fueron los primeros en obtener antimateria con ayuda de la luz
Aquella primera “sopa de plasma primordial” posibilitó que se juntaran protones y neutrones para formar el elemento más simple del Universo: El Hidrógeno. El elemento número uno de la Tabla Periódica que, evolucionado en las estrellas nos lleva a la complejidad de la materia.
La luz y otros tipos de radiación interaccionan fuetemente con partículas libres eléctricamente cargadas, del tipo de las que existen en el plasma que constituía el universo antes de que los átomos se formaran. A causa de esta interacción, cuando la radiación se mueve por el plasma, colisiona con partículas, rebotando y ejerciendo una presión del mismo modo que las moléculas de aire, al rebotar sobre las paredes de un neumático, mantienen el neumático inflado, Si se diese el caso de que una conglomeración de materia del tamaño de una galaxia tratase de formarse antes de la congelación de los átomos, la radiación que traspasaría el material habría destruído el conglomerado. Por la misma razón, la radiación tendería a quedar atrapada dentro de la materia. Si tratase de salir, sufriría colisiones y rebotaría.

No es fácil sobreestimar la importancia de esta afirmación. Lo que significa es que mientras que la materia permaneció como plasma (es decir, mientras los átomos no se habían congelado) ninguna galaxia podría haberse foremado, o ni siquiera empezado a formarse. Se deduce que hubo un período determinado, que comenzó alrededor de los 100.000 años, en el que tuvo lugar la formación de Galaxias. Antes de ese Tiempo, la interacción de la radiación con la materia habría impedido que se formace cualquier cosa como nuestro Universo actual.
El problema de es explicar la existencia de la galaxias ha resultado ser uno de los más espinosos de la cosmología. Con todo derecho no deberían estar ahí y, sin embargo, ahí están. Es difícil comunicar el abismo de frustración que este simple hecho produce entre los científicos. Una y otra vez han surgido nuevas revelaciones y ha parecido que el problema estaba resuelto. Cada vez la solución se debilitaba, aparecían nuevas dificultades que nos transportaban al punto de partida.

Cada pocos años, la American Physical Society, la Asociación Profesional de físicos, tienen una sesión en una de sus reuniones en la que los Astrofísicos hablan de los más nuevos métodos de afrontar el problema de las galaxias. Si te molestas en asistir a varias de esas reuniones, dos son las sensaciones contradictorias que te embargan: Por una parte sientes un gran respeto por la ingenuidad de algunas propuestas que son hechas “de corazón” y, desde luego, la otra sensación es la de un profundo excepticismo hacia las ideas que allí se proponen, al escuchar alguna explicación de cómo las turbulencias de los agujeros negros, las explosiones durante la formación de galaxias, los neutrinos pesados y la materia oscura fría resolvía todos aquellos problemas…, puedes llegar a la conclusión de que, en verdad, no sabemos nada y queremos, ocultar nuestra ignorancia con prupuestas ¿descabellas? Bueno, algunas veces sí.
Lo cierto es que, a pesar de lo que se pueda leer en la prensa en comunicados oficiales y otros medios, todavía no tenemos ese “bálsamo milagroso” que nos permita responder a una pregunta simple:
¿Por qué está el Universo lleno de galaxias?
emilio silvera
Abr
1
Vivir para ver
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
El superordenador más bonito del mundo está en una capilla de Barcelona. Esto nos cuentan en un reportaje de prensa.
Realiza 13.700 billones de operaciones cada segundo y es utilizado por investigadores de toda Europa para, por ejemplo, diseñar tratamientos a medida para enfermedades como el cáncer
La ciencia y la religión parecen haber hallado un lugar de encuentro en el barrio de Pedralbes de Barcelona. Allí, en el Centro Nacional de Supercomputación, una capilla acoge al superordenador más potente de España: el Mare Nostrum 4. La imagen del ultramoderno superordenador acristalado en el interior de un templo, enmarcado por arcos, columnas y vidrieras, le ha valido el título de la supercomputadora más bonita del mundo, concedido por la plataforma global de información sobre centros de datos DatacenterDynamics y elegido por el público formado por profesionales de la industria. El lugar impresiona: un vestíbulo de cristal se superpone al exterior de la fachada de la capilla y, al entrar, la recepción de seguridad y unos tornos recuerdan que lo que pisas ya no es suelo divino —la capilla fue desacralizada en 1985—. El interior está delimitado por una caja de vidrio que abarca el espacio central. Dentro, en lugar de bancos y un altar, hay decenas de armarios de metal negros cada uno del tamaño de un frigorífico: son las estructuras que almacenan los procesadores.

Es un paisaje infinito de lucecitas intermitentes y cables organizados por colores: entre 60 y 80 kilómetros de cable hacen posible que el cerebro del ordenador funcione. Una doble puerta de seguridad da acceso a la pecera que protege los armarios. La entrada es por turnos, solo se puede acceder de uno en uno y utilizando una tarjeta y una huella dactilar. El murmullo que se percibe desde fuera se convierte en lo que podría ser el zumbido de miles de abejas una vez que cruzas la puerta. Son los 13.700 billones de operaciones que los procesadores del Mare Nostrum 4 realizan cada segundo.
Pero este mastodonte es mucho más que un centro de datos bonito. Investigadores de toda Europa lo utilizan para trabajar en proyectos relacionados con la salud, el clima, el desarrollo de inteligencia artificial y nuevas formas de energía. Ahora mismo, están desarrollando modelos para predecir la dispersión del polvo del Sáhara, que modifica la agricultura de Almería o las Islas Canarias y afecta a las personas con dolencias pulmonares.

Los cálculos del Mare Nostrum 4 también pueden mejorar e incluso salvar vidas. Distintos proyectos investigan el ADN para desarrollar medicina personalizada: el equipo de Josep Tabernero, oncólogo y uno de los mayores expertos en cáncer de colon del país, utiliza su capacidad de cálculo para identificar distintos tratamientos dependiendo del tipo de tumor que tenga el paciente. En esta misma línea se mueve el equipo de Bonaventura Clotet, una eminencia en la investigación del sida, que ha conseguido identificar hasta diez tipos distintos de virus y estudia posibles vacunas personalizadas teniendo en cuenta la variante y las características del paciente.Otros equipos están investigando cómo desarrollar tejidos del corazón a partir de células madre para obtener parámetros que permitan recrear simulaciones antes de intervenir a los pacientes.
El cambio climático es otra de las líneas de investigación habituales. Los cálculos del ordenador sirven para identificar y predecir la calidad del aire de las ciudades, lo que podría servir para controlar la contaminación. También muestra a los investigadores cómo afectará lo que estamos haciendo ahora a las condiciones ambientales del futuro y cuáles serán los cambios principales que se producirán en la temperatura, las lluvias y el nivel del mar dentro de unos años. Tener esta información hace posible que podamos tomar medidas con antelación. Algunas de estas investigaciones han sido reconocidas por la comunidad científica y publicadas en prestigiosas revistas como Science o Nature.

De alguna forma el Mare Nostrum 4 es una máquina del tiempo: los modelos que se desarrollan hacen simulaciones y predicen el comportamiento de los fenómenos que se estudian. “En total, por estos procesadores han pasado más de 3.000 proyectos científicos”, explica Mateo Valero, director del Centro Nacional de Supercomputación y padre del ordenador. “No damos servicio a empresas privadas, el centro está financiado por un consorcio del Gobierno, la Generalitat y la Universidad de Barcelona. Nuestro objetivo es que los investigadores de toda Europa puedan utilizar gratis el ordenador para seguir creando ciencia”, asegura Valero. Y continúa: “Es muy importante que España tenga uno de estos centros de investigación, ¡es uno de los pilares básicos (pero no el único) para tener ciencia! Y si un país no produce ideas, no es competitivo”.

El centro funciona con 34,3 millones de euros de presupuesto, que vienen de las instituciones españolas, pero también de la Comisión Europea. Y sale rentable. “Por cada euro que nos dan para investigar, generamos 15”, continúa Valero. ¿Por qué ha crecido tanto? “Tenemos una máquina que hace en un día lo que en 2004 necesitaba un año: es 300 veces más potente y consume solo cinco veces más energía que el Mare Nostrum 1”. El director se refiere al primer superordenador que acogió la capilla, hace 14 años. En ese momento, después de llevar mucho tiempo construyendo sus propias máquinas, Valero recibió la propuesta de gestionar e instalar en el campus de la Universidad Politécnica de Barcelona —a la que pertenece la capilla— el primer superordenador: una máquina que iba a desarrollar IBM para la que el Gobierno buscaba un hogar. “Teníamos un hándicap muy importante: solo nos daban cuatro meses para montarlo ¡y ni siquiera sabíamos dónde meterlo!”, cuenta Sergi Girona, director de operaciones del centro. “Necesitábamos un espacio de 160 metros cuadrados, sin columnas que entorpecieran, alto y disponible. Solo teníamos la capilla”.

No fue una tarea fácil. Las peculiaridades del edificio les obligaron a pensar en soluciones creativas, no solo para meter los armarios con los procesadores por la única puerta de madera que hay disponible, sino para ubicar los sistemas de refrigeración y los transformadores eléctricos necesarios para que la máquina funcione. “Un superordenador como este necesita unas condiciones ambientales y de mantenimiento muy específicas”, explica Girona. La temperatura dentro del espacio acristalado tiene que mantenerse en torno a los 24 grados pero hace falta mucho más que la refrigeración por aire para que eso sea posible. “Cada armario genera el calor de 20 secadores de pelo encendidos a la vez”, cuenta Girona. “Por eso hemos instalado el sistema de refrigeración por puerta trasera”. Eso significa que unas tuberías llevan agua fría hasta la parte de atrás de los armarios, para que puedan eliminar el calor que expulsan.
Toda la maquinaria que mantiene el ordenador en buenas condiciones (los equipos que generan el agua fría, los transformadores, los generadores eléctricos…) está fuera, bajo el suelo y en una caseta insonorizada. En el caso de que se vaya la luz, unas baterías se conectan automáticamente. “Mantener el ordenador solo con los acumuladores durante mucho tiempo cuesta demasiado”, explica Girona. “Y ya en condiciones normales gastamos alrededor de un millón y medio de euros al año en electricidad”.
Otro de los factores importantes es la humedad del ambiente. Y quien consigue que esté en su medida exacta es el encargado de mantenimiento. Al principio gastaban mucho dinero intentando controlar la humedad relativa y no lo conseguían. “Hasta que un día ví a Paco [el chico de mantenimiento] limpiando los cristales”, cuenta Girona. “Desde entonces nuestro método es un mocho y una bayeta escurridos y a limpiar: así conseguimos subir la humedad hasta el grado necesario”.
Precisamente los cristales que rodean y protegen al superordenador se han convertido en una característica que identifica este centro de datos porque contrasta con la imagen de otros superordenadores, donde el contenido de los armarios se esconde y protege con códigos de seguridad. En muchos casos, sucede porque son centros privados que guardan información sensible de empresas que imponen sus propios requisitos de seguridad. En este caso, el Centro Nacional de Supercomputación está protegido por cámaras de infrarrojos, seguridad continua, métodos de detección temprana de incendios —realizan un análisis de aire que detecta si se va a producir un incendio tres días antes de que un humano pueda olerlo— y sistemas de acceso biométricos. “No perdemos nada mostrando las tripas del ordenador a los visitantes”. De hecho, les gusta presumir de ello y hasta el más mínimo detalle está cuidado. Reina la simetría y todo tiene una razón de ser.
También son conscientes de que la belleza del lugar atrae a más visitantes. El año pasado recibieron 10.300 visitas. Miles de personas que van hasta Barcelona para ver la supercomputadora dentro de una capilla. Merece la pena cuidarlo, sobre todo cuando una de esas visitas es un escritor de renombre internacional, autor de best sellers como El código Da Vinci. Dan Brown visitó el centro de datos en 2015 con el objetivo de buscar inspiración para su último libro, Origen. Volvió 14 meses después con ejemplares de regalo para los trabajadores. A lo largo de la trama, uno de los personajes principales utiliza el superordenador para realizar cálculos con el objetivo de dar respuesta a las preguntas “¿de dónde venimos?” y “¿a dónde vamos?”. Estas dos cuestiones traen de cabeza a la religión y la ciencia, que han competido a lo largo de toda la historia para darles respuesta. El centro parece el lugar perfecto para ambientar la ficción de Brown porque la dicotomía entre ciencia y religión es un tema recurrente en su bibliografía. Al fin y al cabo, tal y como se puede leer en el libro, “a menudo, la ciencia y la religión pretenden contar la misma historia en dos lenguajes distintos”.
















 Totales: 75.603.433
Totales: 75.603.433 Conectados: 3
Conectados: 3


























